Расчет высоковольтного конденсатора 6 кВ
1. Электрический расчет
Исходные данные:
Uном= 35кВ; Iном=200 А;
Реактивная мощность Qр=65 кВАр, среднеквадратическое отклонение δ=7 кВ. Число перенапряжений в год 104. Длительность одного перенапряжения 10-2 с.
Определение емкости
10.1 Трехфазный конденсатор состоит из трех сборок секций, которые могут быть соединены либо в звезду , либо в треугольник. Примем соединение сборок секций в треугольник. Тогда на каждую сборку будет действовать линейное напряжение, а её емкость найдем из формулы реактивной мощности:
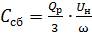 =1.917 мкФ
=1.917 мкФ
Определение числа последовательно отключенных секций
10.2 Принимаем толщину бумаги δ1=12 мкм. Число слоев между обкладками n1=6
и рабочую напряженность поля Ераб=14 МВ/м. Находим:
nпосл=Uраб/ Ераб∙ n1∙ δ1=5.952 (1.22)
Примем nпосл=6 и n1=7; тогда рабочая напряженность поля:
Ераб= Uн / nпосл∙ n1∙ δ1=11.9 МВ/м
10.3 Рабочее напряжение секции:
Uс= Ераб∙ n1∙ δ1=1 кВ
Определение размеров и числа параллельных секций
10.4 Предварительно зададимся размерами секции: толщина ∆с=20, длина b=280 и ширина h=160 мм. Определим длину закраины:
∆l=k3∙ Uисп+l1=8.3 мм
, где k3=1.5 мм/кВ-коэффициент закраины; l1=5 мм-допуск на технологическое смещение фольги при намотке секций.
10.5 Испытательное напряжение секции составит:
Uисп=2.2Uраб / nпосл=2.2 кВ
10.6 Находим относительную диэлектрическую проницаемость пропитанной трихлордифенилом бумаги: (при u2δ2=0)
εr= εr.пр/1+( γб/ γк) ∙ kз∙ [(εr.пр/ εrк)-1]=5.819
Для силового конденсатора принята бумага КОН-1 плотностью γб=1000 кг/м3.Коэффициент запрессовки kз=0.9. Относительная диэлектрическая проницаемость трихлордифенила εr.пр=5.
10.7 Найдем емкость секции:
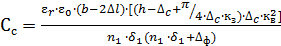 =4.3∙
=4.3∙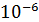 Ф
Ф
при ∆ф=8мкм.
10.8 Число параллельных секций:
nпар=(Ссб∙ nпосл)/ Сс=2.675
10.9 Округлим число параллельных секций до nпар=3. Тогда требуемая емкость секции равна:
Сс=(Ссб∙nпосл)/ nпар=3.834*10-6 Ф
Выбор материала корпуса конденсатора
10.10 Выбираем металлический корпус с толщиной стенки 0.5 мм. Изоляцию от корпуса и между пакетами конденсатора изготавливают из кабельной бумаги, толщина которой определяется исходя из:
Uмр=2.2∙Uн∙кзап=39.6 кВ ; ∆к=0.96 мм
Секции в корпусе располагают к стенкам корпуса широкой стороной, чтобы уменьшить перепад температур в секции. Секции собираются в пакеты. Каждая сборка содержит 1 пакет, состоящий из 18 последовательно и параллельно включенных секций. Между секциями прокладывается прокладка из одного листа кабельной бумаги толщиной ∆пр=12 мм. Пакеты секции обматываются кабельной бумагой толщиной 0.96 мм (изоляция от корпуса) и скрепляются стальными бандажными лентами.
10.11 Размеры пакета:
высота hп= nпосл∙ nпар∙∆с+ nпосл∙ nпар∙∆пр+2∆к=364.08 мм;
ширина bп=h+2∆к=161.92 мм;
длина lп=b+2∆к=281.92 мм;
10.12 Размеры корпуса конденсатора :
высота hк= hп+2∆к+∆з=381 мм;
ширина bк= bп+2∆м=162.92 мм;
длина lк=3lп+2∆м=846.76 мм.
При определении высоты корпуса учтен зазор ∆з=15 мм, необходимый для размещения проходного изолятора.
2.2. Тепловой расчет
Секции конденсатора делают со скрытой фольгой.
11.1 Зададим значения температур в точке: +70, +40, +10 0С. При заданных температурах tgδ70=0.0023, tgδ40=0.0019 и tgδ10=0.0021. Диэлектрические потери равны:
Рд70=Uc2∙ ω∙Cc∙ tgδ70=2.769 Вт
Рд40=Uc2∙ ω*Cc∙ tgδ40=2.287 Вт
Рд10=Uc2∙ ω*Cc∙ tgδ10=2.528 Вт
11.2 Активная длина обкладки:
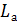 =
=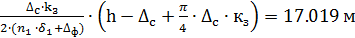
11.3 Потери в обкладках при n=1:
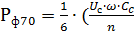 )2
)2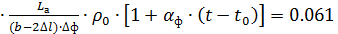 Вт
Вт
Соответственно Рф40=0.059 Вт, Рф10=0.052 Вт.
11.4 Тепловыделения в секции составят:
Рс70= Рд70+ Рф70=2.83 Вт
Рс40= Рд40+ Рф40=2.346 Вт
Рс10= Рд10+ Рф10=2.58 Вт
11.5 Удельное тепловыделение в секции:
q70= Рс70/[(b-2∆l)∙ h∙∆c]=3357 Вт/м3
q40= Рс40/[(b-2∆l) ∙h∙∆c]=2784 Вт/м3
q10= Рс10/[(b-2∆l) ∙h∙∆c]=3061 Вт/м3
11.6 Перепад температур на участке 1-2:
∆t1= q70∙ [(h-∆c)2/8 λэкв1]=3.15 0С
λэкв1=(λ1∙n1∙ δ1+ λф∙∆ф)/ (n1∙ δ1+∆ф)=18.652 (Вт/м∙0С)
11.7 Теплопроводность пропитанной бумаги λ1=1 (Вт/м*0С). Теплопроводность фольги λф=204 (Вт/м*0С). Перепад температур на участке 2-3:
∆t2= q70∙∆c2/8 λэкв2∙ [1+(h-∆c)/ ∆c)]=1.227 0С
λэкв=(n1∙ δ1+∆ф)/ (n1∙ δ1/λ1)+(∆ф/λф)=1.095 (Вт/м∙0С)
11.8 Тепловыделение в изоляции от корпуса:
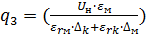 2
2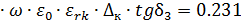 Вт/м2
Вт/м2
Толщину зазора между изоляцией и корпусом примем ∆м=1 мм, tgδз=0.0023 –значение пропитанной бумаги при t=66.7 0C.
11.9 Перепад температур на участке 3-4:
∆t3= (q70∙h/2+q3/2)∙( ∆к/λ)=0.258 0С
при λ=1.
11.10 Тепловыделение в зазоре между изоляцией и корпусом:
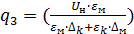 2
2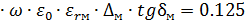 Вт/м2
Вт/м2
tgδм=0.002 для трихлордифенила при t=66.4 0C.
При толщине жидкостной прослойки 1мм можно пренебречь конвективным теплообменом.
11.11 Перепад температур:
∆t4= (q70∙h/2+ q3+q5/2) ∙ ( ∆м/λэкв)=0.26 0С
Теплопроводность трихлордифенила λ=0.1 (Вт/м∙0С).
11.12 Находим тепловыделение в конденсаторе, пренебрегая потерями в соединительных проводах:
Q= Рс70∙ nпосл∙ nпар+q3∙Sк+ q5∙ Sк=51.309 Вт
11.13 Поверхность корпуса конденсатора:
Sк=2hк∙ (bк+lк)+2 bк∙ lк=1.042 м2
11.14 Перепад температур в стенке корпуса:
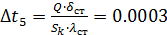 0С (1.55)
0С (1.55)
Теплопроводность стали 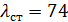 Вт/(м∙0С).
Вт/(м∙0С).
11.15 Температура на поверхности корпуса:
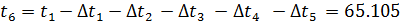 0С
0С
11.16 Перепад температур от стенки в окружающую среду определим по методике [1] описанной в Ş 5.6
Зададимся перепадом температур 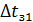 =6.1 0С, тогда температура окружающей среды
=6.1 0С, тогда температура окружающей среды 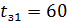 0С.
0С.
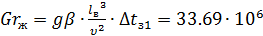 (1.56)
(1.56)
Определяющий размер l=hи=0.381 м, 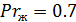 ,
, 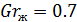
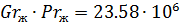
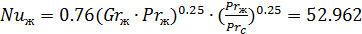 (1.55)
(1.55)
11.17 Находим коэффициент теплоотдачи при конвективном теплообмене.
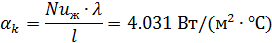
11.18 Поверхность охлаждения корпуса:
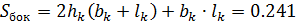 м2
м2
Перепад температур от стенки конструкции в окружающую среду
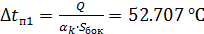 (1.80)
(1.80)
Так как ∆tп1 не равно 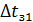 , то зададимся
, то зададимся 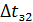 =44.6
=44.6 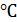 и
и 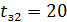 0С и проведем повторный расчет:
0С и проведем повторный расчет:
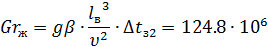
при 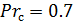 ,
, 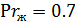
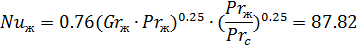
11.19 Находим коэффициент теплоотдачи при конвективном теплообмене.
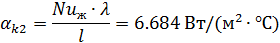
11.20 Перепад температур от стенки конструкции в окружающую среду
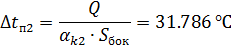













 (zip - application/zip)
(zip - application/zip)










