ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Хабаровский институт инфокоммуникаций (филиал)
ФГОБУ ВПО
«Сибирский государственный университет телекоммуникаций и информатики»
Факультет Инфокоммуникаций и Систем Связи
Кафедра ОПД
КУРСОВАЯ РАБОТА
по дисциплине «Теория электрических цепей»
Тема: «РАСЧЕТ ПАРАМЕТРОВ ПАССИВНЫХ ЧЕТЫРЁХПОЛЮСНИКОВ»
Выполнил: студент 2 курса ФИКСС
группа ИТ-31
шифр 31024
Ящук Олег Игоревич
Проверил: доцент
Горбунова Н.Г. _______________
г. Хабаровск-2015
 ЗАДАНИЕ
ЗАДАНИЕ
На курсовую работу по дисциплине «Теория электрических цепей»
Студенту 2 курса направления ИТ и СС факультета ФИКС
Ящуку Олегу Игоревичу
(фамилия, имя, отчество)
Тема: «Расчет параметров пассивных четырёхполюсников»
Исходные данные:
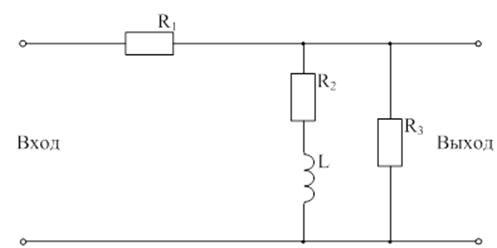
R1 = 290 Ом
R2 = 300 Ом
R3 = 600 Ом
Rг =0.5*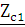 Ом
Ом
Rн = 2*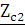 Ом
Ом
L = 0.2 Гн
ω = 2700 рад/с
Функция реакции: iL
 Содержание пояснительной записки:
Содержание пояснительной записки:
1. Определить А-параметры четырехполюсника.
2. Выполнить проверку выполнения основного соотношения между ними.
3. Определить вторичные параметры четырехполюсника (входное и выходное характеристические сопротивления и постоянную передачи четырёхполюсника).
4. Определить входное, выходное характеристические сопротивления и постоянную передачи двух каскадно-соединенных согласованных четырехполюсников.
5. Вывести формулы амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристик.
6. Используя одну из прикладных программ (Электронная скамья WEWB, MATHCAD или другую) получить графики АЧХ и ФЧХ и внести их в пояснительную записку.
7. Определить переходную и импульсную характеристики четырехполюсника, пользуясь классическим и операторным методами.
Дата выдачи задания: « » ______________20___года
Дата сдачи проекта на проверку: « » _______________20___ года
Задание принял к исполнению: /_________________/
Руководитель курсового
проекта: доцент Горбунова Н.Г. /_________________/
 СОДЕРЖАНИЕ:
СОДЕРЖАНИЕ:
|
1. Задание на курсовое проектирование |
|
|
2. Введение |
|
|
3. Определение А-параметров четырехполюсника. |
|
|
4. Проверка А-параметров 5. Расчет параметров холостого хода и короткого замыкания |
|
|
6. Определение вторичных параметров четырехполюсника (входное и выходное характеристические сопротивления и постоянная передачи четырёхполюсника) |
|
|
7. Расчет рабочей меры передачи четырехполюсника 8. Определение характеристических сопротивлений и постоянной передачи двух каскадно-соединенных согласованных четырёхполюсников |
|
|
9. Вывод формул АЧХ и ФЧХ |
|
|
10. Графики АЧХ и ФЧХ |
|
|
11. Определение переходной и импульсной характеристики четырехполюсника 12. Расчет цепи в виде тока на индуктивности при подаче на вход единичного напряжения |
|
|
13. Заключение |
|
|
14. Список используемой литературы |
|
 Введение.
Введение.
В технике связи под четырехполюсником понимают электрическую цепь (или ее часть) любой сложности, имеющую две пары зажимов для подключения к источнику и приемнику электрической энергии. Зажимы, к которым подключается источник, называются входными, а зажимы, к которым присоединяется приемник (нагрузка), — выходными зажимами (полюсами).
Предлагаемая курсовая работа содержит задание на расчет параметров пассивных четырехполюсников. Студенту выдается индивидуальная распечатка со схемой и цифровыми данными, на основании которой определяются А-параметры четырехполюсника, производится их проверка, определяются вторичные параметры четырехполюсника (входное и выходное характеристические сопротивление и постоянна передачи четырёхполюсника), определяются входные, выходные характеристические сопротивления и постоянная передачи двух каскадно-соединенных согласованных четырехполюсников, производится вывод формулы амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристик. Используя одну из прикладных программ (Электронная скамья WEWB, MATHCAD или другую) нужно получить графики АЧХ и ФЧХ и внести их в пояснительную записку. Определяется переходная и импульсная характеристика четырехполюсника, пользуясь классическим и операторным методами.
 ХОД РАБОТЫ
ХОД РАБОТЫ
1. Определить А-параметры четырехполюсника
Аналитические отношения токи и напряжения на входе и на выходе четырехполюсника называются уравнениями передачи четырехполюсника. Величины связывающие токи и напряжения в этих уравнениях называют параметрами четырехполюсника.
В системе уравнений с А-параметрами ток 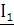 и напряжение
и напряжение 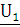 на входных зажимах определяются через ток
на входных зажимах определяются через ток 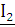 и напряжение
и напряжение  на выходных зажимах.
на выходных зажимах.
Запишем уравнения А-параметров для четырехполюсника:
|
|
(1.1) |
|
А-параметры имеют
следующий физический смысл: 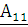 – величина обратная коэффициенту
передачи по напряжению,
– величина обратная коэффициенту
передачи по напряжению,  – сопротивление на входных зажимах
четырехполюсника,
– сопротивление на входных зажимах
четырехполюсника, 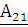 – проводимость на выходных зажимах четырехполюсника,
– проводимость на выходных зажимах четырехполюсника, 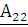 – величина обратная коэффициенту передачи по току.
– величина обратная коэффициенту передачи по току.
1.1 Расчет эквивалентных сопротивлений
данного четырехполюсника
Для нахождения А-параметров данного
четырехполюсника (рис. 1.1.1), заменим сопротивление R1 на эквивалентное сопротивление 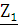 , а сопротивленя R2, R3, XL, соединенные
последовательно-параллельно, на эквивалентное сопротивление
, а сопротивленя R2, R3, XL, соединенные
последовательно-параллельно, на эквивалентное сопротивление 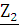 , (рис. 1.1.2).
, (рис. 1.1.2).

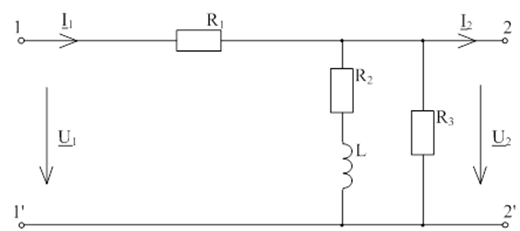
Рис. 1.1.1 - схема четырехполюсника, данная по условию
Для этого рассчитаем комплексное сопротивление индуктивности для заданной циклической частоты ω = 2700 рад/с:
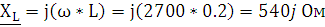
Рассчитаем эквивалентные
сопротивления 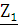 ,
, 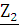 :
:
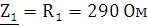
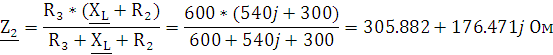
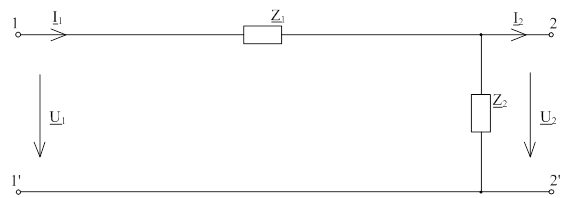
Рис. 1.1.2 - схема четырехполюсника, данная по условию,
с присвоенными индексами Z
 1.2 Расчет А-параметров
четырехполюсника методом
1.2 Расчет А-параметров
четырехполюсника методом
холостого хода и короткого замыкания
Рассчитаем параметры 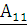 и
и 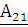 методом
холостого хода. При применении метода холостого хода выходные зажимы разомкнуты
(
методом
холостого хода. При применении метода холостого хода выходные зажимы разомкнуты
(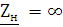 ), откуда
), откуда
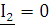 .
.
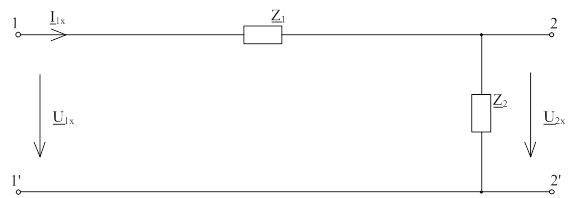
Рис. 1.2.1 - Схема четырехполюсника при холостом ходе
Учитывая это преобразуем уравнения А-параметров четырехполюсника (стр.6 1.1):
|
|
(1.2.1) |
|||
|
где |
|
||
|
|
|||
|
|
|||
Выразим из
данных уравнений (1.2.1) параметры 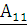 и
и 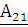 :
:
|
|
(1.2.2) |
|
|
|
(1.2.3) |
Рассчитаем по полученным формулам (1.2.2; 1.2.3) А-параметры:
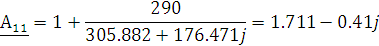
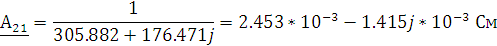
 Для применения метода короткого
замыкания закорачиваем выходные зажимы (
Для применения метода короткого
замыкания закорачиваем выходные зажимы (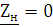 ) откуда
) откуда 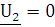 .
.
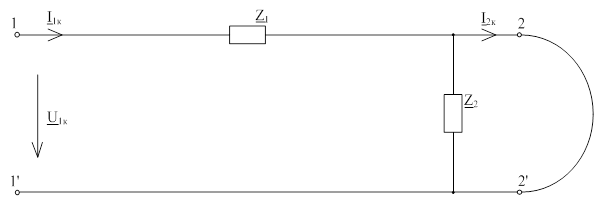 Рис. 1.2.2 - Схема четырехполюсника при коротком
замыкании.
Рис. 1.2.2 - Схема четырехполюсника при коротком
замыкании.
Так
как 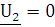 , то из уравнений А-параметров
четырехполюсника (стр.6 1.1) следует:
, то из уравнений А-параметров
четырехполюсника (стр.6 1.1) следует:
|
|
(1.2.4) |
|||
|
где |
|
||
|
|
|||
|
|
|||
Выразим параметры из уравнений (1.2.4)
 и
и 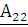
|
|
(1.2.7) |
|
|
|
(1.2.8) |
Рассчитаем эти параметры с помощью полученных выражений (1.2.7; 1.2.8)
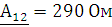
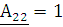
 1.3 Проверка
1.3 Проверка
Для проверки правильности расчетов А-параметров применим правило: определитель матрицы А-параметров обратимого четырехполюсника должен быть равен 1.
Матрица А-параметров имеет вид (1.3.1):
|
|
(1.3.1) |
Составим выражение для нахождения ее определителя (1.3.2)
|
|
(1.3.2) |
Рассчитаем определитель матрицы А-параметров данного четырехполюсника:
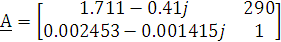
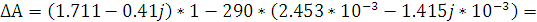
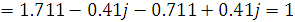
 Определитель матрицы составленной из
А-параметров четырехполюсника равен 1, следовательно расчет А-параметров
произведен верно.
Определитель матрицы составленной из
А-параметров четырехполюсника равен 1, следовательно расчет А-параметров
произведен верно.
 2. Расчет параметров холостого хода и
короткого замыкания
2. Расчет параметров холостого хода и
короткого замыкания
через найденные А-параметры и непосредственно по схеме четырехполюсника
Параметрами холостого хода и короткого замыкания называют сопротивление четырехполюсника со стороны входных или выходных зажимов (рис. 2.1, 2.2).

Рис. 2.1 - Входное сопротивление со стороны зажимов 1-1’

Рис. 2.2 - Входное сопротивление со стороны зажимов 2-2’
2.1 Расчет параметров холостого хода
Для расчета параметров 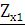 ,
, 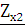 применим метод холостого хода, при
котором сопротивление нагрузки
применим метод холостого хода, при
котором сопротивление нагрузки 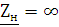 , откуда
, откуда 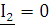 (рис.
2.1.1; 2.1.2).
(рис.
2.1.1; 2.1.2).


Рис. 2.1.1 - Входное сопротивление со стороны зажимов 1-1’при холостом ходе
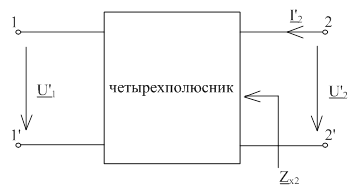
Рис. 2.1.2 - Входное сопротивление со стороны
зажимов 2-2’при холостом ходе
Из уравнений А-параметров для холостого хода (стр. 8 1.2.1 , 1.2.2)
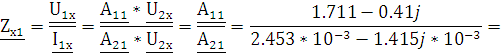
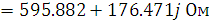
При изменении направления передачи энергии через
четырехполюсник коэффициенты 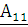 и
и 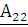 меняются
местами
меняются
местами
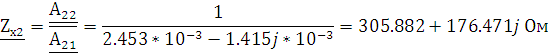
2.2 Расчет параметров короткого замыкания
Для
расчета параметров 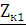 ,
,  применим метод короткого замыкания,
применим метод короткого замыкания,
при котором сопротивление нагрузки 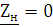 , откуда
, откуда 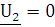 .
.


Рис. 2.2.1 - Входное сопротивление со стороны зажимов 1-1’
при коротком замыкании

Рис. 2.2.2 - Входное сопротивление со стороны зажимов 2-2’
при коротком замыкании
Из полученных ранее уравнений А-параметров для короткого замыкания (стр.9 1.2.5, 1.2.6)
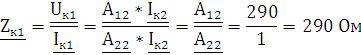
При изменении направления передачи энергии через
четырехполюсник коэффициенты 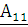 и
и 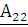 меняются
местами
меняются
местами
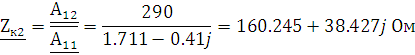
 2.3 Расчет параметров холостого хода
и короткого замыкания непосредственно по схеме четырехполюсника
2.3 Расчет параметров холостого хода
и короткого замыкания непосредственно по схеме четырехполюсника
Рассчитаем параметры 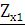 ,
, 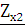 ,
, 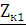 ,
,  непосредственно по схеме. Для
расчета используем закон Ома (2.3.1)
непосредственно по схеме. Для
расчета используем закон Ома (2.3.1)
|
|
(2.3.1) |
Составим уравнения параметров для каждого случая применения методов холостого хода и короткого замыкания.
Сопротивление
холостого хода при разомкнутых зажимах 2-2’ 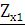 определяется напряжением
определяется напряжением  на зажимах 1-1’ и током
на зажимах 1-1’ и током 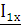 протекающим во входном контуре
четырехполюсника через последовательно соединенные сопротивления
протекающим во входном контуре
четырехполюсника через последовательно соединенные сопротивления 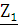 и
и 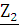 (рис. 2.3.1).
(рис. 2.3.1).
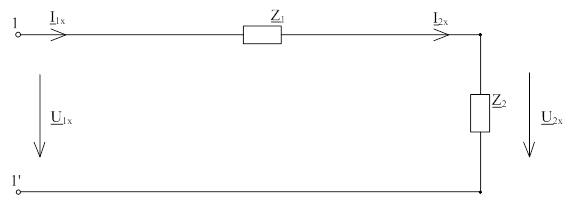
Рис. 2.3.1 –
Схема четырехполюсника при 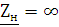
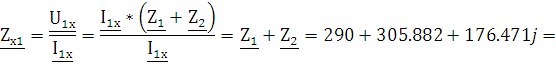
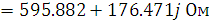
Сопротивление
холостого хода при разомкнутых зажимах 1-1’ 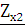 определяется напряжением
определяется напряжением 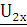 на зажимах 2-2’ и током
на зажимах 2-2’ и током 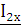 протекающем в выходном контуре четырехполюсника
через сопротивление
протекающем в выходном контуре четырехполюсника
через сопротивление 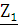 (рис. 2.3.2).
(рис. 2.3.2).
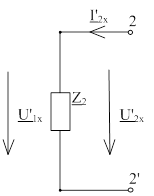
Рис. 2.3.2 –
Схема четырехполюсника при 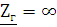 ,
,
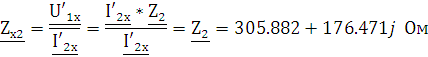
Сопротивление
короткого замыкания при закороченных зажимах 2-2’ 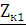 определяется напряжением
определяется напряжением  на зажимах 1-1’ и током
на зажимах 1-1’ и током 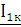 протекающим в четырехполюснике через
сопротивление
протекающим в четырехполюснике через
сопротивление 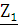 (рис. 2.3.3).
(рис. 2.3.3).


Рис. 2.3.3 –
Схема четырехполюсника при 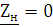
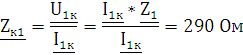
Сопротивление
короткого замыкания при закороченных зажимах 1-1’  определяется напряжением
определяется напряжением  на зажимах 1-1’ и током
на зажимах 1-1’ и током 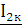 протекающим в четырехполюснике через
параллельно соединенные сопротивления сопротивление
протекающим в четырехполюснике через
параллельно соединенные сопротивления сопротивление 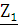 и
и 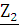 (рис. 2.3.1).
(рис. 2.3.1).
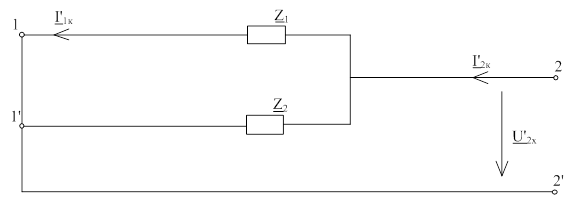
Рис. 2.3.4 –
Схема четырехполюсника при 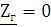
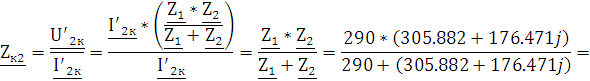

2.4 Проверка
Параметры холостого хода и короткого замыкания выполнены верно, если выполняется условие (2.4.1):
|
|
(2.4.1) |
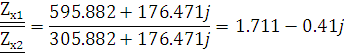
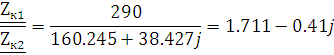
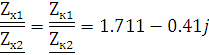
Условие вы полняется, параметры рассчитаны верно.
полняется, параметры рассчитаны верно.
 3. Определение вторичных параметров
четырехполюсника (входное и выходное характеристическое сопротивление и постоянная
передачи четырёхполюсника)
3. Определение вторичных параметров
четырехполюсника (входное и выходное характеристическое сопротивление и постоянная
передачи четырёхполюсника)
При передаче энергии через четырехполюсник стараются применять
согласованный режим передачи, то есть входное сопротивление четырехполюсника 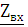 должно
быть согласовано с сопротивлением генератора
должно
быть согласовано с сопротивлением генератора 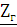 , а
сопротивление нагрузки
, а
сопротивление нагрузки 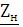 – с
выходным сопротивлением четырехполюсника
– с
выходным сопротивлением четырехполюсника 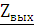 .
.
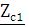 и
и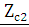 – это такая пара сопротивлений для которых выполняются
условия (3.1, 3.2)
– это такая пара сопротивлений для которых выполняются
условия (3.1, 3.2)
|
|
(3.1) |
|
|
|
(3.2) |
То есть при включении сопротивления 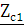 на входные зажимы четырехполюсника,
его выходное сопротивление будет равняться
на входные зажимы четырехполюсника,
его выходное сопротивление будет равняться 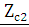 (рис. 3.1), а при включении
сопротивления
(рис. 3.1), а при включении
сопротивления 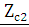 на выходные зажимы, входное
сопротивление четырехполюсника будет равным
на выходные зажимы, входное
сопротивление четырехполюсника будет равным 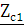 (рис. 3.2).
(рис. 3.2).

Рис. 3.1 - Четырёхполюсник с согласованной нагрузкой на входе.
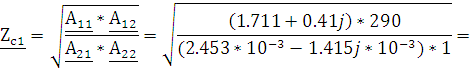
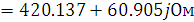

Р ис. 3.2 - Четырёхполюсник с согласованной нагрузкой на выходе.
ис. 3.2 - Четырёхполюсник с согласованной нагрузкой на выходе.
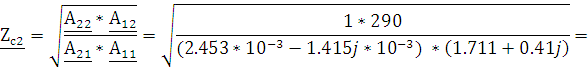
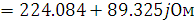
Постоянная передачи четырехполюсника – мера передачи энергии через согласованный четырехполюсник, которая связывает токи и напряжения на входе и выходе, определяется из соотношений (3.1, 3.2):
|
|
(3.1) |
|
|
|
(3.2) |

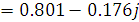
Ас = 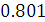 Нп
Нп
Bc = 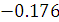 рад
рад
 Рассчитаем вторичные параметры четырехполюсника
через параметры холостого хода
Рассчитаем вторичные параметры четырехполюсника
через параметры холостого хода 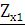 ,
, 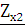 и короткого замыкания
и короткого замыкания 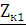 ,
,  и сверим с найденными:
и сверим с найденными:

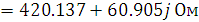
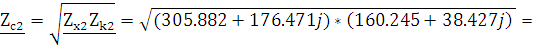
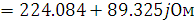
Рассчитанные параметры полностью совпали.
 4. Определить входное, выходное
характеристические сопротивления и постоянную передачи двух
каскадно-соединенных согласованных четырехполюсников
4. Определить входное, выходное
характеристические сопротивления и постоянную передачи двух
каскадно-соединенных согласованных четырехполюсников
При каскадном согласованном соединении четырехполюсников выходные зажимы одного четырехполюсника соединяются с выходными зажимами другого четырехполюсника (рис. 4.1).
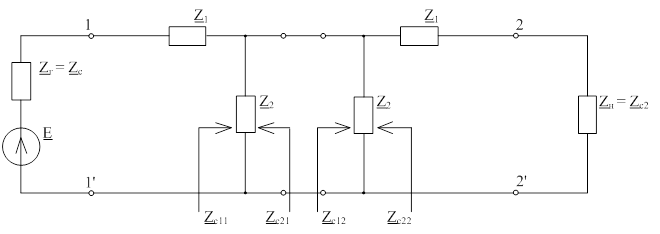 Рис. 4.1 – Каскадное согласованное соединение
четырехполюсников
Рис. 4.1 – Каскадное согласованное соединение
четырехполюсников
Так как четырехполюсники
соединены согласовано, то 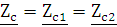 :
:
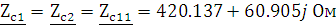
Постоянная передачи 2-х каскадно-согласованных четырехполюсников:
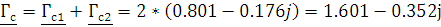
Ac = 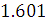 Нп
Нп
Bc = 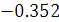 рад
рад
5. Рассчитать рабочую меру передачи четырехполюсника
Рабочая мера передачи характеризует потери энергии возникающие в реальном режиме работы четырехполюсника. Рабочая мера передачи рассчитывается как сумма потерь энергии на входе, на выходе, энергии теряемой при многократном отражении от входных и выходных зажимов и собственной постоянной передачи четырехполюсника её можно найти через собственное рабочее ослабление четырехполюсника:
|
|
Рассчитаем сопротивления генератора и нагрузки:
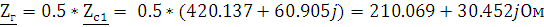

Рассчитаем коэффициенты отражения на входе, и на выходе:
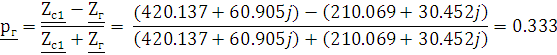
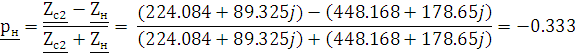
Применим уравнение расчета собственного рабочего ослабления четырехполюсника, с полученными коэффициентами отражения
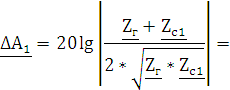
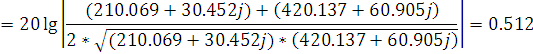
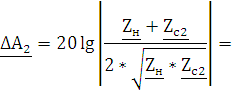
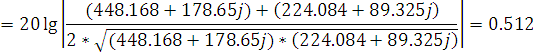
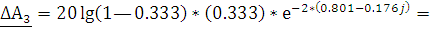
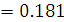
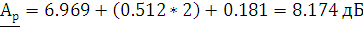
 |
6. Вывести формулы
амплитудно-частотной (АЧХ) и
Вывести формулы
амплитудно-частотной (АЧХ) и
фазо-частотной (ФЧХ) характеристик.
Передаточной функцией нагруженного четырехполюсника, называют отношение реакции цепи к воздействию. Если входным воздействием считать напряжение генератора с комплексным действующим значением Uг, а реакцией четырехполюсника на это воздействие - напряжение с комплексным действующим значением U2 или ток с комплексным действующим значением I2, то получаются комплексные передаточные функции общего вида (6.1; 6.2):
|
|
(6.1) |
|
|
|
(6.2) |
В частных случаях, когда заданными воздействиями являются напряжение на входных зажимах четырехполюсника или ток, протекающий через эти зажимы, получают следующие четыре разновидности передаточных функций (6.3)
|
|
(6.3) |
||
|
где |
HU – комплексный коэффициент передачи по напряжению; |
||
|
HY - комплексный коэффициент передачи по проводимости; |
|||
|
Hi - комплексный коэффициент передачи по току; |
|||
|
Hz - комплексный коэффициент передачи по сопротивлению. |
|||
Можно вычислять передаточные функции в различных режимах работы четырехполюсника (6.4; 6.5):
|
|
(6.4) |
|
|
|
(6.5) |
Физическим смыслом передаточной функции является нахождение амплитудно-частотной (АЧХ) и фазово-частотной (ФЧХ) характеристик (6.6).
|
|
(6.6) |
 Модуль комплексной
передаточной функции показывает во сколько раз изменилось гармоническое
напряжение на выходе нагруженного четырехполюсника по сравнению с его значением
на входе и называется амплитудно-частотной характеристикой (АЧХ) (6.7)
Модуль комплексной
передаточной функции показывает во сколько раз изменилось гармоническое
напряжение на выходе нагруженного четырехполюсника по сравнению с его значением
на входе и называется амплитудно-частотной характеристикой (АЧХ) (6.7)
|
|
(6.7) |
Фазово-частотная характеристика (ФЧХ) определяет сдвиг фаз между гармоническими колебаниями на входе и выходе четырехполюсника (6.8)
|
|
(6.8) |
Все выше сказанное так же характерно и для передаточной функции по току (6.9; 6.10)
|
|
(6.9) |
|
|
|
(6.10) |
Рассчитаем
передаточную функцию операторным методом, примем 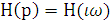 (6.11)
(6.11)
|
|
(6.11) |
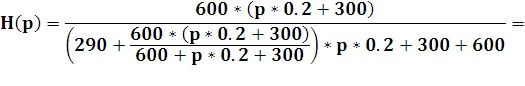
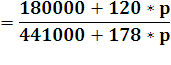
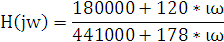
АЧХ найдем из соотно шения (6.12):
шения (6.12):
|
|
(6.12) |
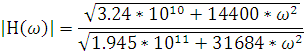
Фазо-частотная характеристика (ФЧХ) — частотная зависимость разности фаз между выходным и входным сигналами (6.13).
|
|
(6.13) |
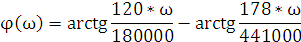
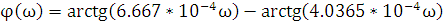
 7. Используя одну из прикладных
программ (электронная скамья WEWB, MATHCAD или другую) получить графики АЧХ и ФЧХ и внести их в
пояснительную записку.
7. Используя одну из прикладных
программ (электронная скамья WEWB, MATHCAD или другую) получить графики АЧХ и ФЧХ и внести их в
пояснительную записку.
Графики построенные с помощью программы MathCAD приведены на рис.7.1; 7.2.
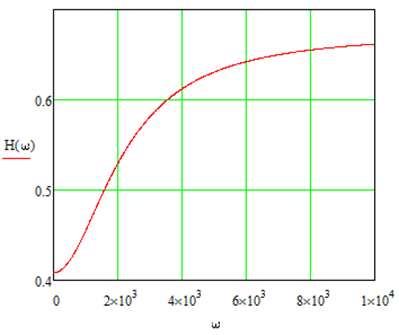
Рис. 7.1 - график АЧХ
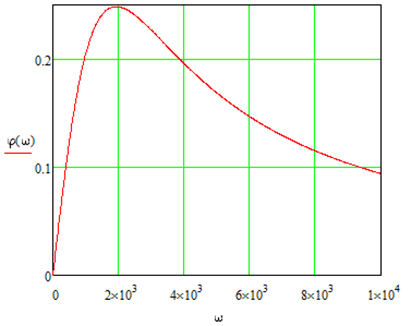
Рис. 7.2 - график ФЧХ
Для проверки правильности
построения графика АЧХ рассчитаем передаточную функцию при частоте 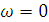 (рис. 7.3) и
(рис. 7.3) и 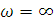 (рис. 7.4).
(рис. 7.4).
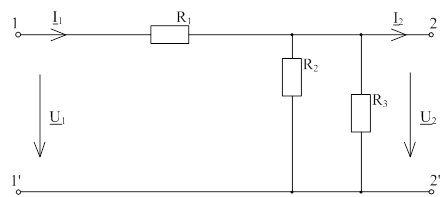
Рис. 7.3 - схем а четырехполюсника при
а четырехполюсника при 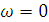
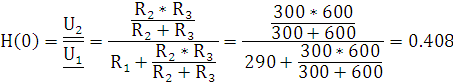
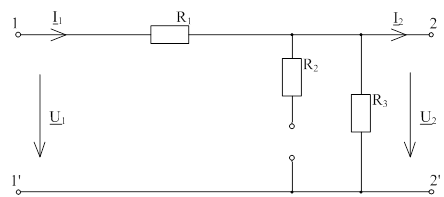
Рис. 7.4 - схема
четырехполюсника при 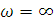
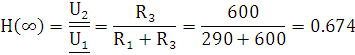
 8. Определить переходную и
импульсную характеристики четырехполюсника, пользуясь классическим и
операторным методами.
8. Определить переходную и
импульсную характеристики четырехполюсника, пользуясь классическим и
операторным методами.
Переходная характеристика четырехполюсника - это реакция цепи на единичное входное воздействие (8.1 рис. 8.1).
|
|
(8.1) |
Рис. 8.1 – переходная характеристика четырехполюсника
Импульсная характеристика четырёхполюсника определяется как реакция на входное воздействие. Импульсная характеристика - это производная от переходной характеристики
Найдем передаточную функцию операторным методом (8.2; 8.3)
|
|
(8.2) |
Найдем изображение переходной характеристики (8.3)
|
|
(8.3) |
Н айдем полюсы и нули, используя
теорему разложения (8.4)
айдем полюсы и нули, используя
теорему разложения (8.4)
|
|
(8.4) |
||
|
где |
pk-корни полинома F2(p). |
||
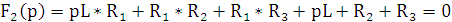
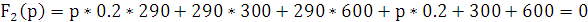
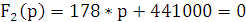
p1
= 0 p2 = 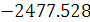
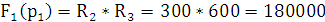
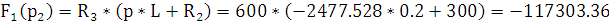
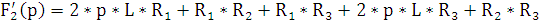
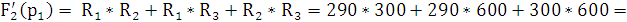
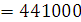
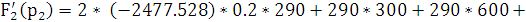
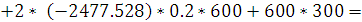
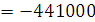
Подставим все найденные значения в формулу переходной характеристики
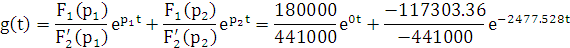
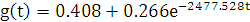
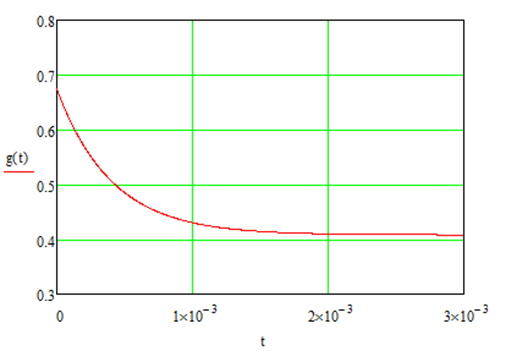
Рис. 8.2 - гр афик переходной характеристики
афик переходной характеристики

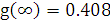
Проверка:
При t = 0:

Рис. 8.3 - эквивалентная схема четырехполюсника в первый момент времени после коммутации
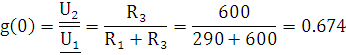
При t = 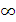 :
:
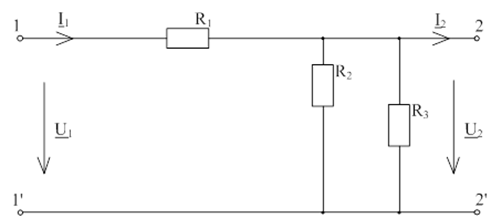
Рис. 8.4 - эквивалентная
схема четырехполюсника через бесконечно больш ой период времени после коммутации
ой период времени после коммутации
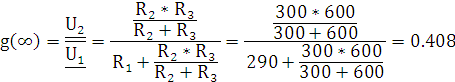
Импульсная характеристика:
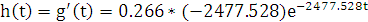
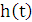 =
=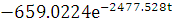
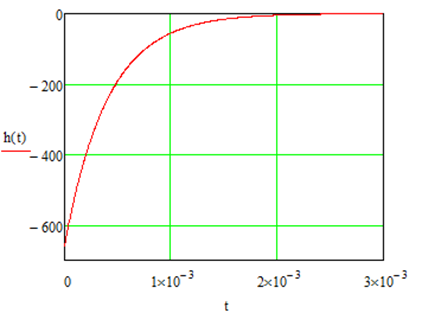
Рис. 8.5 – график импульсной характеристики
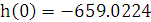
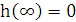
9. Рассчитать реакцию цепи в виде тока на индуктивности при подаче на вход единичного скачка напряжения
Найде м полное сопротивление
четырехполюсника (9.1)
м полное сопротивление
четырехполюсника (9.1)
|
|
(9.1) |
Используя движение токов и напряжения получим (9.2)
|
|
(9.2) |
Сопротивление на индуктивности (9.3)
|
|
(9.3) |
Напряжение на индуктивности (9.4)
|
|
(9.4) |
Функция реакции по току (9.5)
|
|
(9.5) |
Найдём полюсы и нули:
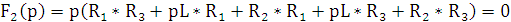
p1
= 0 p2 = 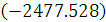
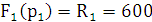
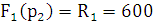
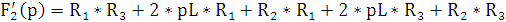
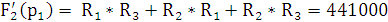
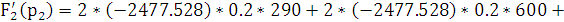
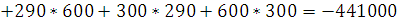
Найдём зависимость функции реакции от времени
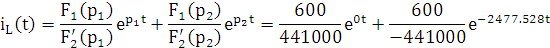
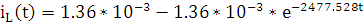
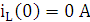
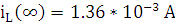
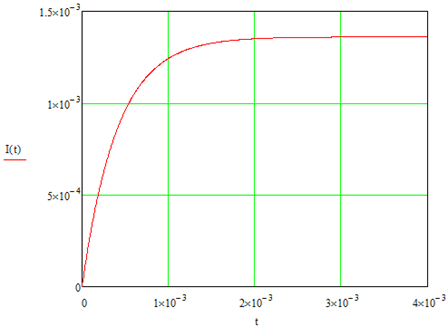
Рис. 9.1 Г рафик функции реакции
рафик функции реакции
Проверка:
При t = 0 XL = ∞, получаем:

Рис. 16 Схема четырехполюсника в начальный момент времени t = 0.
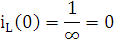
При t = 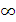 XL =
XL =  , получаем:
, получаем:
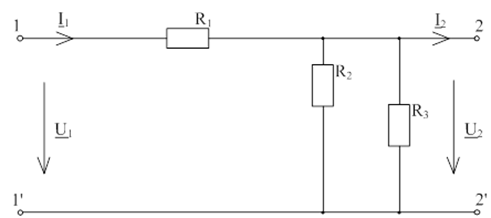
Рис. 17. Схема
четырехпо люсника в бесконечный момент времени t =
люсника в бесконечный момент времени t = 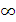 .
.
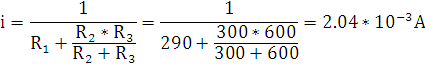
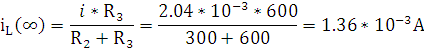
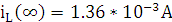
Заключение
В данном курсовом проекти ровании был проанализирован четырёхполюсник.
Были найдены А – параметры, определены характеристические сопротивления и
постоянная передачи одного и двух каскадно соединенных четырёхполюсников,
построены графики АЧХ и ФЧХ, определена переходная и импульсная характеристики четырёхполюсника
разными методами. Сделаны все возможные проверки.
ровании был проанализирован четырёхполюсник.
Были найдены А – параметры, определены характеристические сопротивления и
постоянная передачи одного и двух каскадно соединенных четырёхполюсников,
построены графики АЧХ и ФЧХ, определена переходная и импульсная характеристики четырёхполюсника
разными методами. Сделаны все возможные проверки.
Все пункты задания курсового проектирования выполнены.
Список использованной литературы:
1. Конспект лекций.
2. В.П.Бакалов. ,В.Ф. Дмитриков., Б.И. Крук. Основы
теории цепей.-М.: Горячая линия-Телеком,2009.
,В.Ф. Дмитриков., Б.И. Крук. Основы
теории цепей.-М.: Горячая линия-Телеком,2009.
3. П.П. Воробиенко. Теория линейных электрических цепей. Сб. задач и упражнений.-М.: Радио и связь, 1989.














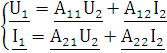
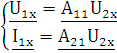
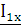 - ток в четырехполюснике при
режиме холостого хода;
- ток в четырехполюснике при
режиме холостого хода;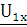 - напряжение между входными
зажимами четырехполюсника при режиме холостого хода;
- напряжение между входными
зажимами четырехполюсника при режиме холостого хода; 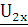 - напряжение между выходными
зажимами четырехполюсника при режиме холостого хода.
- напряжение между выходными
зажимами четырехполюсника при режиме холостого хода. 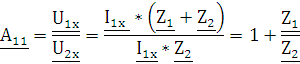
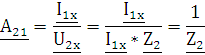

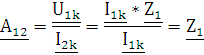
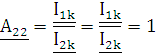
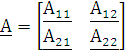
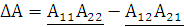
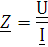
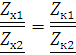
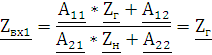
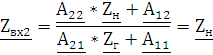

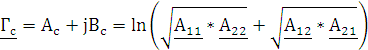
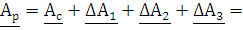
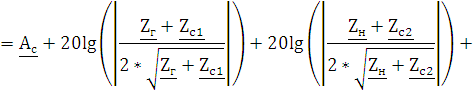
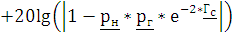
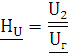
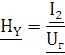
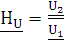 ;
; 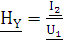 ;
; 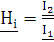 ;
; 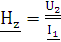 .
.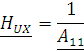
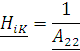
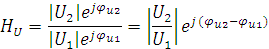
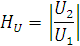
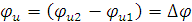
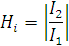
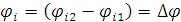
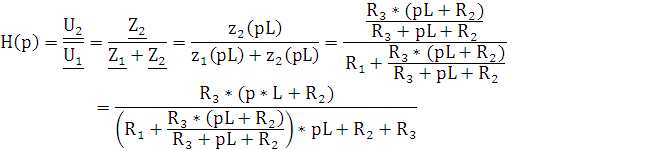
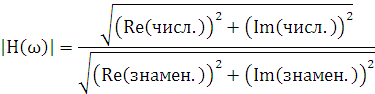
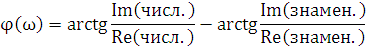

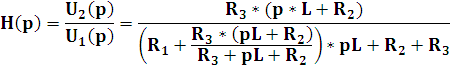
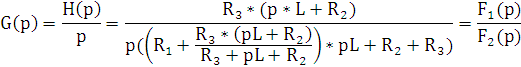
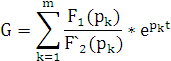
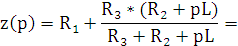
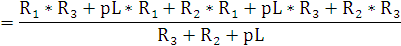
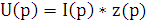
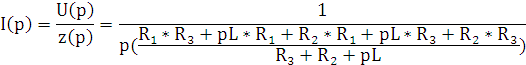
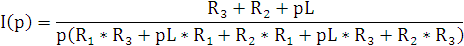
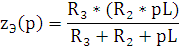

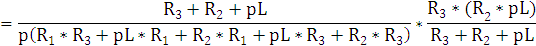
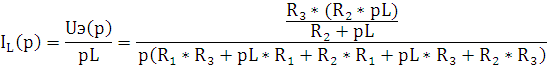
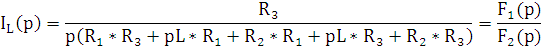
 (zip - application/zip)
(zip - application/zip)











