Проверка гипотезы о законе распределения генеральной совокупности X по критерию Пирсона

ФБГОУ ВПО «Сибирская государственная автомобильно-дорожная

академия (СибАДИ)»

Кафедра «Высшая математика»

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА

по дисциплине «Высшая математика»

на тему: «Проверка гипотезы о законе распределения генеральной совокупности X по критерию Пирсона» (Вариант №22)

Выполнил: студент гр. ПГСб-11В1

Беимов С. С.

Проверила: Мирошниченко Т. П.

Омск-2012

Содержание

1.     Исходные данные

2.     Вариационный ряд

3.     Интервальный вариационный ряд

4.     Гистограмма. Выдвижение гипотезы о законе распределения генеральной совокупности X

5.     Теоретическая функция плотности рассмотренного закона. Оценки числовых характеристик и оценки параметров закона

6.     Проверка критерия Пирсона

1.  Исходные данные

Математической статистикой называется наука о методах получения и обработки результатов наблюдений (измерений) для установления закономерностей в массовых случайных явлениях. В математической статистике решается 2 типа задач:

1.     Оценивание- получение точечных и интервальных оценок некоторых параметров или числовых характеристик.

2.     Статистическая проверка гипотез заключается в проверке согласованности результатов эксперимента с предлагаемой гипотезой о распределении вероятностей случайной величины.

Генеральной совокупностью называется совокупность всех возможных наблюдений, проводимых в одинаковых условиях над некоторыми случайными величинами.

Отобранные из генеральной совокупности объекты называются выборкой.

Число объектов данной выборки называется объемом выборки (n).

Дана выборка из генеральной совокупности случайной величины X:

Табл. 1

Генеральная совокупность

10.7	6.6	15.9	19.1	11.6	17.4	14.9	13.2
15.9	7.4	14.0	9.5	17.7	8.7	7.2	8.8
16.6	7.3	11.9	9.3	9.5	12.5	10.5	10.2
12.8	17.6	15.5	7.3	12.9	12.7	11.4	9.0
14.5	9.2	17.8	8.9	6.8	16.2	7.7	8.0
14.7	14.1	15.0	17.1	9.5	16.6	17.2	9.6
16.6	8.1	11.6	6.8

n= 52-объем выборки.

2.     Вариационный ряд

После того как из генеральной совокупности извлечена выборка, ее объекты обследуют по отношению к генеральной совокупности, для этого их подвергают обработке.

Операция заключается в том, что элементы выборки располагают в порядке их возрастания, называемое ранжированием, а последовательность элементов называется вариационным рядом, а элементы называются вариантами.

Табл. 2

Ранжированный ряд

6.6	6.8	6.8	7.2	7.3	7.3	7.4	7.7
8.0	8.1	8.7	8.8	8.9	9.0	9.2	9.3
9.5	9.5	9.5	9.6	10.2	10.5	10.7	11.4
11.6	11.6	11.9	12.5	12.7	12.8	12.9	13.2
14	14.1	14.5	14.7	14.9	15	15.5	15.9
15.9	16.2	16.6	16.6	16.6	17.1	17.2	17.4
17.6	17.7	17.8	19.1

Диапазон наблюденных значений случайной величины X укладывается в интервал (6;20). Ранжированные опытные данные объединяем в группы.

Численность отдельной группы сгруппированного ряда опытных данных называется выборочной частотой соответствующей варианты X⁽ⁱ⁾ и обозначается: - выборочная частота,

При этом

Отношение выборочной частоты данной варианты к объему выборки называется относительной выборочной частотой и находится по формуле:

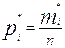, где i-номер варианта, причем

3. Интервальный вариационный ряд

Интервальным вариационным рядом распределения называется упорядоченная совокупность частичных интервалов значений случайных величин, с соответствующими им частотами или относительной частотой.

Для построения вариационного ряда выполняются следующие действия:

1. Находим размах выборки:

R=X_наиб.-X_наим.

R=19.1-6.6=12.5

2. Назначаем количество частичных интервалов k=11

Находим шаг разбиения ∆:

При этом округление производим до ближайшего целого числа или до ближайшей простой дроби.

3. После разбиения на частичные интервалы рассмотрим ранжированную выборку и определяем, сколько значений признака попало в каждый частичный интервал. В итоге получаем интервальный вариационный ряд.

Табл. 3

Интервальный вариационный ряд

N	xi – xi+1	i	mi*	pi*= mi*/n	hi*= pi*/∆	hi .pi	mi*- npi	(mi*- npi)2	(mi*- npi)2 npi
1	6;7	6,5	3	0,057	0,057	4,16	-1,16	1,35	0,32
2	7;8	7,5	5	0,096	0,096	4,16	0,84	0,71	0,17
3	8;9	8,5	5	0,096	0,096	4,16	0,84	0,71	0,17
4	9;10	9,5	7	0,135	0,135	4,16	2,84	8,07	1,94
5	10;11	10,5	3	0,057	0,057	4,16	-1,16	1,35	0,33
6	11;12	11,5	4	0,077	0,077	4,16	-0,16	0,03	0,01
7	12;13	12,5	4	0,077	0,077	4,16	-0,16	0,03	0,01
8	13;14	13,5	1	0,19	0,19	4,16	-3,16	9,99	2,40
9	14;15	14,5	5	0,096	0,096	4,16	0,84	0,71	0,17
10	15;16	15,5	4	0,077	0,077	4,16	-0,16	0,03	0,01
11	16;17	16,5	4	0,077	0,077	4,16	-0,16	0,03	0,01
12	17;18	17,5	6	0,115	0,115	4,16	1,84	3,39	0,14
13	18;19	18,5	0	0	0	4,16	-4,16	17,31	1
14	19;20	19,5	1	0,019	0,019	4,16	-3,16	9,99	0,76
Сумма			52	1					7,74

Где 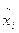- середина i-ого интервала;

t_i –нормированная нормальная случайная величина i-ого интервала;

p_i – вероятность попадания возможных значений случайной величины в i-ый интервал.

4. Гистограмма. Выдвижение гипотезы о законе распределения генеральной совокупности X

Гистограмма – это изображение интервального ряда, представляющее собой ступенчатую фигуру, состоящую из прямоугольников с основаниями равными длине интервала 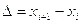 и высотой  .

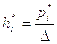Гистограмму строят только для непрерывной генеральной совокупности. Гистограмма является оценкой генеральной функции плотности f(x).

Рис. 1- Гистограмма

Вид данной гистограммы позволяет выдвинуть гипотезу о равномерном законе распределения исследуемой случайной величины.

5. Теоретическая функция плотности рассмотренного закона.  

Оценки числовых характеристик и оценки параметров закона

Оценками математической статистики называют приближенные значения числовых характеристик или параметров законов распределения генеральной совокупности X, вычисленные на основе выборки.

Оценка называется точечной, если она определяется одним числом или точкой на числовой оси.

Выборочной средней (оценкой математического ожидания) называется среднее арифметическое значение признака выборочной совокупности.

Выборочная дисперсия (оценка дисперсии) – это среднее арифметическое квадратов отклонений вариант от их выборочной средней.

Найдем оценки М(х) и D(х).

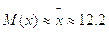
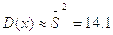
Найдем оценки параметров a и b равномерного распределения:

 ;         

Следовательно  

После, находим функцию плотности f(x)

Следовательно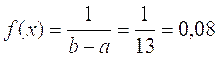

Найдем

т.к. закон распределения равномерный, то на всех интервалах P_i=0,08

6. Проверка критерия Пирсона

Критерии такого рода, когда выявляется согласие между распределением выборки и теоретическим распределением, называют критерием согласия. Наиболее употребляемым и простым критерием для проверки статистических гипотез является критерий Пирсона (χ²). Вероятность Ɛ, которую выбирают в зависимости от ситуации, называют уровнем значимости, а вероятность 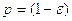- доверительной вероятностью.

Критерий согласия Пирсона находится по формуле:

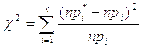
По результатам вычислений, приведенных выше в таблице получаем χ² =7,74

Определим число степеней свободы для нормального закона:

                                                 r= k - q,                                                     

где k- количество объединенных интервалов;

q – число независимых условий («связей»), наложенных на относительные частоты p_i^* (для нормального закона распределения q=3).

r=7-3=4

Выберем уровень значимости 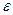  = 0,01 и по таблице для r=5 найдем   χ² =9,5. Так как наблюденное значение χ² оказалось меньше табличного значения, то есть произошло событие (χ²_в > χ² _0,05;4), вероятность которого равна 0,95, то можно сделать вывод: выдвинутая гипотеза о равномерном законе распределения принимается по опытным данным.