
Доклад
по учебной дисциплине
«Теория Алгоритмов»
на тему:
«Происхождение рекурсных функций, простейшие рекурсные функции. Операторы суперпозиции и примитивные рекурсии. Понятие примитивно рекурсивной функции.»
Выполнил : курсант 223 учебной группы
Малахов И.Д
Происхождение и основные понятия теории рекурсивных функций.
Рекурсивные функции - (от позднелатинского recursio — возвращение)
название, закрепившееся за одним из наиболее распространённых вариантов уточнения общего понятия арифметического алгоритма, т.е. такого Алгоритма, допустимые исходные данные которого представляют собой системы натуральных чисел, а возможные результаты применения являются натуральными числами. Рекурсивные функции были введены в 30-х гг. 20 в. С. К. Клини, в свою очередь основывавшимся на исследованиях К. Гёделя, Ж. Эрбрана и др. математиков.
Каждая рекурсивная функция задаётся конечной системой равенств точно охарактеризованного типа в том смысле, что её значения вычисляются с помощью этой системы равенств по точно формулируемым правилам, причём таким образом, что в итоге для вычисления значений заданной рекурсивной функции получается алгоритм определённого типа.
Арифметические функции, для вычисления значений которых имеются какие-либо алгоритмы, принято называть вычислимыми. Вычислимые функции играют в математике важную роль. Вместе с тем, если понятию алгоритма здесь не будет придан точный смысл, то и само понятие вычислимой функции окажется несколько расплывчатым. Рекурсивные функции уже в силу самого характера своего определения оказываются вычислимыми.
Рекурсивные функции являются частичными функциями, т. е. функциями, не обязательно всюду определёнными. Чтобы подчеркнуть это обстоятельство, часто в качестве синонима используют термин «частично рекурсивные функции». Рекурсивные функции, определённые при любых значениях аргументов, называют общерекурсивными функциями.
Определению рекурсивных функций может быть придана следующая форма: Фиксируется небольшое число чрезвычайно простых исходных функций, вычислимых в упомянутом выше интуитивном смысле (функция, тождественно равная нулю, функция прибавления единицы и функции, выделяющие из системы натуральных чисел член с данным номером); фиксируется небольшое число операций над функциями, переводящих вычислимые функции снова в вычислимые (операторы подстановки, примитивной рекурсии и минимизации). Тогда рекурсивные функции определяются как такие функции, которые можно получить из исходных в результате конечного числа применений упомянутых выше операций.
Операции над функциями.
Оператор суперпозиции (подстановки) сопоставляет функции f от n переменных и функциямg1, . . ., gn от m переменных функцию h от m переменных такую, что для любых натуральных чисел x1, .., xm
h(x1, .., xm) ≅ f (g1(x1, .., xm), ..., gm(x1, .., xm))
(здесь и ниже условное равенство ≅ означает, что оба выражения, связываемые им, осмыслены одновременно и в случае осмысленности имеют одно и то же значение).
Оператор примитивной рекурсии сопоставляет функциям f от n переменных и g от n + 2 переменных функцию h от n + 1 переменных такую, что для любых натуральных чисел x1, .. .., xn, y
h(x1, .., xn ,0) ≅ f(x1, .., xn),
h(x1, .., xn, y + 1) ≅ g(x1, .., xn, y, h(x1, .., xn, y )).
Примеры. Приведем некоторые примеры частично рекурсивных функций.Пример 1. Постоянные функции.
Пусть fn(x1,...,xn)=k для всех наборов
аргументов (x1,...,xn) и числа 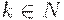 .
Тогда
.
Тогда
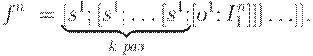
Пример 2. Сложение: x2(x,y)=x+y.
Функция сложения определяется следующей примитивной рекурсией.
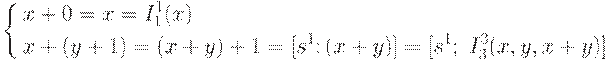
Следовательно, +2 =R(I11,[s1;I33]).
Пример 3. Умножение: x2(x,y)=x x y.
Используя сложение, умножение можно задать следующей примитивной рекурсией:
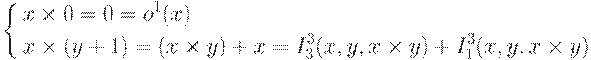
Следовательно, x2 =R(o1,[+;I33,I13]).
Пример 4.
Вычитание : 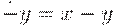 , если x >= y и
, если x >= y и 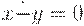 , если x < y.
, если x < y.
Вычитание определяется следующей примитивно рекурсивной схемой:
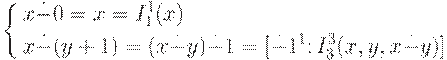
Следовательно, 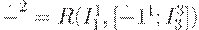 .
.
Пример 5. Модуль разности: 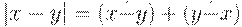 .
.














 (zip - application/zip)
(zip - application/zip)










