Програмування методів чисельного обчислення інтегралів

Текст:

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Буковинський державний фінансово-економічний університет

Факультет комп’ютерних та соціальних технологій

Кафедра комп’ютерних дисциплін

КУРСОВИЙ ПРОЕКТ

з дисципліни «Крос-платформне програмування»

на тему:

“ Програмування методів чисельного обчислення інтегралів”

Виконав студент ІІІ-го курсу

групи КН-31 _________________________ Денис В.М.

(підпис)

Науковий керівник _________________________ Галочкін О.В.

^{(підпис)}

В.О. Завідувач кафедри _________________________ Ащеулов А.А.

^{(підпис)}

Національна шкала _______ Кількість балів _______ Оцінка ECTS _____

Чернівці 2016

ЗМІСТ

ВСТУП .................................................................………………...….…………
..…..3

РОЗДІЛ І. Наближене обчислення визначеного інтеграла методами прямокутників, трапецій та Сімпсона….…………………………………….…….6

1.1 Наближене обчислення визначеного інтеграла методом прямокутників та трапецій…………………………………………………………………………..6

1.2 Наближене обчислення визначеного інтеграла методом Сімпсона……….....9

1.3 Залишковий член формули прямокутників, трапецій, Сімпсона …………....10

РОЗДІЛ II. СЕРЕДОВИЩЕ ПРОГРАМУВАННЯ ECLIPSE.................................14

2.1. Основні характеристики середовища програмування Eclipse ……………...14

2.2. Організація роботи в середовищі програмування Eclipse ……….………….18

РОЗДІЛ ІII. ПРОГРАМНА РЕАЛІЗАЦІЯ АЛГОРИТМУ НАБЛИЖЕНОГО ОБЧИСЛЕННЯ ВИЗНАЧЕНОГО ІНТЕГРАЛУ МЕТОДАМИ ПРЯМОКУТНИКІВ, ТРАПЕЦІЙ ТА СІМПСОНА ……………………………...21

3.1.Практичне використання алгоритму наближеного обчислення визначеного інтеграла методами прямокутників, трапецій та Сімпсона……….………….......21

3.2. Опис програмного продукту "Програмування методів чисельного обчислення інтегралів"…………............................................................................
..26

ВИСНОВКИ ……………………………………………………………………….. 28

СПИСОК ВИКОРИСТАН ЛІТЕРАТУРИ……………………………….………29 ДОДАТКИ

ВСТУП

В сучасному житті ми кожного дня використовуємо математику, чи то для вимірювання відстані, чи для обчислення суми, чи для знаходження різниці. Інколи нам доводиться багаторазово здійснювати одні і ті ж складні обчислення, які не можливі без записів і які забирають чимало цінного часу. Щоб не витрачати час на обчислення однакових прикладів людина створила калькулятор. Цей винахід суттєво полегшив обчислення, але що робити коли справа доходить до знаходження інтегралу. Звичайним калькулятором тут не зарадиш, тому існує потреба в створенні програмного продукту, який обчислював би самостійно складні інтеграли.

Інтеграл - одне з найважливіших понять математики, що виникло у зв"язку з потребою, з однієї сторони відшукувати функції по їхніх похідних (наприклад, знаходити функцію, що виражає шлях, пройдений точкою, що рухається, по швидкості цієї точки), а з іншого боку - вимірювати площі, обсяги, довжини дуг, роботу сил за певний проміжок часу й т.п. Символ інтегралу уведений Лейбніцем. Цей знак є зміною латинської букви S (першої букви слова сума). Саме слово інтеграл придумав Я. Бернуллі. Імовірно, воно походить від латинського іntegero, що переводиться як приводити в колишній стан, відновлювати. Можливе походження слова інтеграл інше: слово іnteger означає цілий.

Виникнення завдань інтегрального вирахування пов"язане зі знаходженням площ й обсягів. Ряд завдань такого роду був вирішений математиками древньої Греції. Антична математика внесла ідеї інтегрального вирахування в значно більшому ступені, чим диференціального вирахування. Більшу роль при рішенні таких завдань грав вичерпний метод, створений Евдоксом Книдським і широко застосовувався Архімедом. Однак Архімед не виділив загального змісту інтеграційних прийомів і понять про інтеграл, а тим більше не створив алгоритму інтегрального вирахування. Учені Середнього й Близького Сходу в ІX-XV ст. вивчали й переводили праці Архімеда на загальнодоступну у їхньому середовищі арабську мову, але істотно нових результатів в інтегральному вирахуванні вони не одержали. Діяльність європейських учених у цей час була ще більш скромною. Лише в XVІ й XVІІ століттях розвиток природничих наук поставило перед математикою Європи ряд нових завдань, зокрема завдання на знаходження квадратур, кубатури і визначення центрів ваги. Праці Архімеда, уперше видані в 1544 р. стали привертати широку увагу, і їхнє вивчення з"явилося одним з найважливіших відправних пунктів розвитку інтегрального вирахування. Архімед передбачив багато ідей інтегрального вирахування. Але треба було більше півтори тисяч років, перш ніж ці ідеї знайшли чітке вираження й були доведені до рівня вирахування.

Математики 17 ст., що одержали багато нових результатів, училися на працях Архімеда. Активно застосовувався й інший метод - метод неподільних, котрий також зародився в Древній Греції. Наприклад, криволінійну трапецію вони уявляли собі складеної з вертикальних відрізків довжиною f(x), яким проте приписували площу, рівну нескінченно малій величині f(x)dx. Відповідно до такого розуміння шукана площа вважалася рівній сумі S = нескінченно великого числа нескінченно малих площ. Іноді навіть підкреслювалося, що окремі доданки в цій сумі - нулі, але нулі особливого роду, які складені в нескінченному числі, дають цілком позитивну суму.

На такій гаданій тепер щонайменше сумнівній основі І. Кеплер у своїх творах "Нова астрономія" (1609) і "Стереометрія винних бочок" (1615) правильно обчислив ряд площ (наприклад площа фігури, обмеженої еліпсом) і обсягів (тіло різалося на нескінченно тонкі пластинки).

В 17 ст. були зроблені багато відкриттів, що ставляться до інтегрального вирахування. Так, П. Ферма вже в 1629 р. вирішив завдання квадратури будь-якій кривій, і на цій основі вирішив ряд завдань на знаходження центрів ваги. Барроу, учитель Ньютона, близько підійшов до розуміння зв"язку інтегрування й диференціювання. Велике значення мали роботи з подання функції у вигляді статечних рядів.

Однак при всій значимості результатів, отриманих з 17 ст., вирахування ще не було. Необхідно було виділити загальні ідеї, що лежать в основі рішення багатьох приватних завдань, а також встановити зв"язок операцій диференціювання й інтегрування , що дає досить точний алгоритм. Але головне вже було зроблено: диференціальне й інтегральне вирахування створене.

Що стосується даної курсової роботи. Об’єктом дослідження є наближене обчислення визначеного інтеграла методом прямокутників, трапецій та Сімпсона.

Об’єктом дослідження є сам процес наближеного обчислення визначеного інтеграла методом прямокутників, трапецій та Сімпсона на базі створеного програмного продукту на базі крос-платформної мови програмування Java.

Метою дослідження є створення якісного програмного продукту, який міг би здійснити складні обчислення по знаходженню інтегралу.

Основним завданням є наближене обчислення визначеного інтеграла методами прямокутників, трапецій та Сімпсона. Для обчислення значення інтеграла, хоча і наближеного, існує прекрасний метод, названий на честь його творця, – метод Сімпсона. Він також називається способом парабол, тому як в ньому використовується побудова параболи. Дана фігура будується максимально наближено до функції. Власне, так як побудувати параболу, у якої точки точно збігаються з точками функції, неможливо, інтеграл і знаходиться наближено .

Метод прямокутників — найпростіший метод чисельного інтегрування. Основна ідея даного методу полягає в тому, що сума площ прямокутників, якими можна замінити функцію на відрізку [a; b], наближається до площі під функцією. Чим менше довжина відрізків, на які ділиться відрізок функції, тим точніше значення шуканого інтеграла.

Метод трапецій є одним з методів чисельного інтегрування. Він дозволяє обчислити визначений інтеграл із заздалегідь визначеною степеню точності.

Основним завданням курсового проекту є реалізація цих методів на базі крос-платформної мови програмування Java.

І. Наближене обчислення визначеного інтеграла методами прямокутників, трапецій та Сімпсона.

1.1. Формули прямокутників і трапеції.

Визначений інтеграл — в математичному аналізі це інтеграл функції з вказаною областю інтегрування. Визначений інтеграл є неперервним функціоналом, лінійним по підінтегральним функціям і адитивним по області інтегрування. У найпростішому випадку область інтегрування — це відрізок числової осі. Геометричний зміст визначеного інтеграла — це площа криволінійної фігури (криволінійної трапеції), обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції.

Подальші узагальнення поняття дозволяють розширити його на кратні, поверхневі, об"ємні інтеграли, а також на інтеграли на об"єктах ширшої природи з мірою. Нехай треба обчислити значення визначеного інтегралу 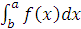, де f(x) є деяка задана на проміжку [a,b] неперервна функція. Існує багато прикладів обчислення подібних інтегралів, або за допомогою первісної, якщо вона виражається в скінченому вигляді, або ж – мінуючи первісну – за допомогою різних прийомів, як правило, штучних. Потрібно відмітити, однак, що всім цим вичерпується вузький клас інтегралів; за його межами зазвичай вдаються до різних методів наближеного обчислення.

В даній роботі можна ознайомитися з основними із цих методів, в яких наближені формули для інтегралів складаються по деякому числу значень підінтегральної функції, обчислених для ряду (зазвичай рівновіддалених) значень незалежної змінної.

Перші формули, які сюди відносяться, простіше всього отримуються із геометричних міркувань. Витлумачуючи визначений інтеграл 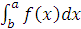, як площу деякої фігури, яка обмежена кривою y=f(x), ми і ставимо перед собою задачу знаходження цієї площі.

Перш за все, вдруге використовуючи ту думку, яка привела нас до самого поняття про визначений інтеграл, можна розбити усю фігуру (Рис 1.1) на смуги, однієї і той же ширини 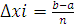, а потім кожну смугу наближено замінити прямокутником, за висоту якого прийнята будь-яка із його ординат. Це приведе нас до формули: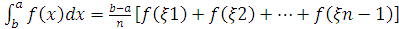, де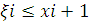
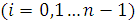. Тут шукана площа криволінійної фігури замінюється площею деякої ступінчатої фігури, яка складається із прямокутників (або ж, можна сказати, що визначений інтеграл замінюється інтегральною сумою). Ця наближена формула і називається формулою прямокутників.

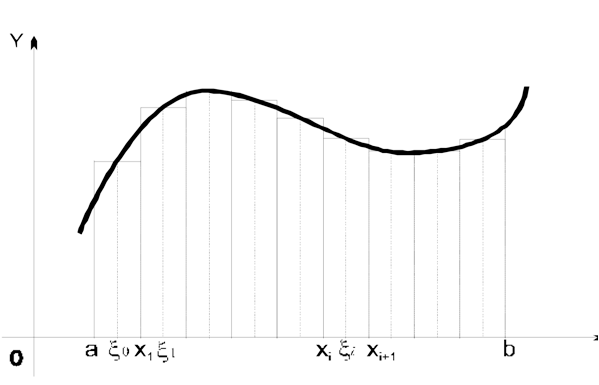Рис 1.1 Розбиття на прямокутники

На практиці зазвичай беруть 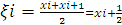якщо відповідну середню ординату 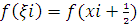позначити через 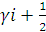, то формула перепишеться у вигляді

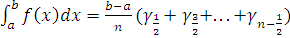. Надалі, кажучи про формулу прямокутників, ми будемо мати на увазі якраз цю формулу.

Геометричні міркування природно приводять і до другої, наближеної формули, що часто використовується. Замінивши дану криву вписаною в неї ламаною, з вершинами у точках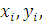 де 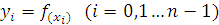. Тоді наша криволінійна фігура заміниться іншою, яка складається із ряду трапецій (мал2.). Якщо, які раніше рахувати, що проміжок [a,b] розбитий на рівні частини, то площі цих трапецій будуть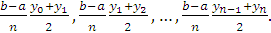

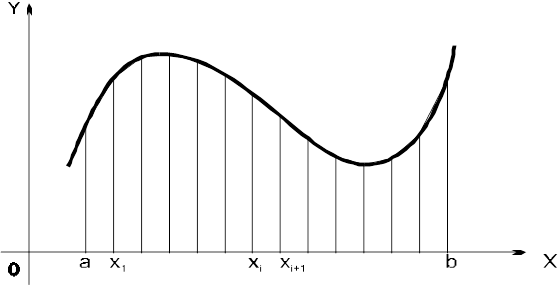
Рис 1.2 Розбиття на трапеції

Додаючи, прийдемо до нової наближеної формули 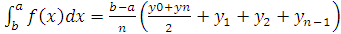Це так звана формула трапецій. Можна показати, що при зростанні 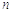до нескінченності похибка формули прямокутників і формули трапецій нескінченно зменшується. Таким чином, при достатньо великому 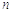обидві ці формули відтворюють шукане значення з довільним рівнем точності.

1.2. Формула Сімпсона

Якщо для кожної пари відрізків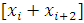 побудувати многочлен другого ступеня, потім про інтегрувати його і скористатися властивістю адитивності інтеграла, то одержимо формулу Сімпсона.

Розглянемо підінтегральну функцію f(x) на відрізку 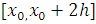. Замінимо цю підінтегральну функцію інтерполяційним многочлен Лагранжа другого ступеня, що збігає з f(x) у крапках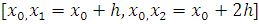

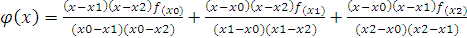
Проінтегруємо::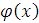

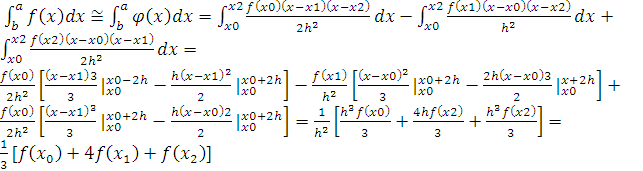
Формула: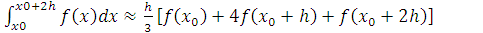

і називається формулою Сімпсона.

Отримане для інтеграла 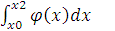значення збігається із площею криволінійної трапеції, обмеженою віссю 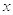, прямими 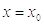, 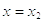і параболою, що проходить через точки

1.3. Залишковий член формули прямокутників, трапецій, Сімпсона.

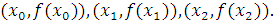
Припустимо, що у проміжку [a,b] функція f(x) має неперервні похідні перших двох порядків. Тоді, розкладаючи f(x) (по формулі Тейлора) за степенями двочлена 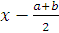аж до його квадрату, будемо мати для всіх значень 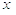в [a,b]

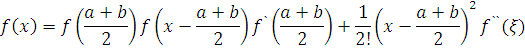
де 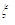міститься між 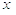та 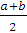і залежить від .

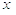Якщо про інтегрувати цю рівність у проміжку від 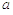до 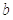, то другий член з права зникне, бо 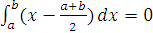. Таким чином, отримаємо 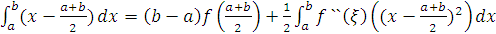, так, що залишковий член формули, який поновлює її точність має вигляд .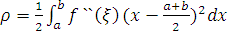

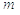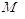Позначивши через і , відповідно найменше та найбільше значення неперервної функції f``(x) у проміжку [a,b] і користуючись тим, що другий множник підінтегрального виразу не змінює знака, за узагальненою теоремою про середнє можемо написати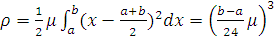

де 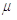міститься між точкам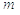и и 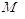. По відомій властивості неперервної функції, знайдеться в [a,b] така точка 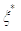, що 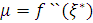, і остаточно: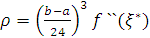

Якщо зараз розділити проміжок [a,b] на 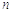рівних частин, то для кожного часткового проміжку 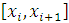будемо мати точну формулу:

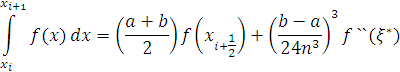
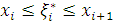Додавши ці рівності (при 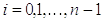) отримаємо при звичайних скорочених позначеннях

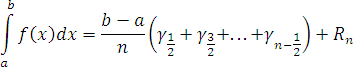
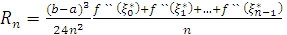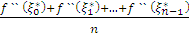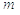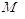Де вираз: і є залишковий член формули прямокутників. Так як вираз: також знаходиться між і , то і він представляє одне із значень функції 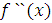. Тому остаточно маємо .

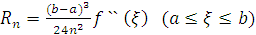Залишковий член формули трапеції.

При попередніх здогадках відносно функції f(x). Скориставшись інтерполяційною формулою Лагранжа із залишковим членом можемо написати

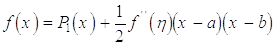
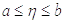Інтегруючи цю формули від 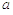до 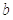, знайдемо

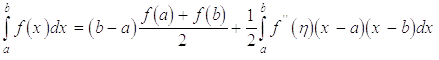так що залишковий член формули (6) буде

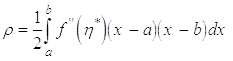Як і вище, і користуючись тим, що другий множник підінтегральної функції і тут не змінює знака, знайдемо

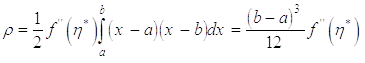
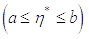Для випадку ділення проміжку на 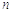рівних частин

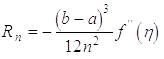Таким є залишковий член формули трапецій. При зростанні 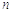він також зменшується приблизно як 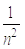. Ми бачимо, що застосування формули трапецій приводить до похибки того ж порядку, що і для формули прямокутників.

Залишковий член формули Сімпсона.

Звернемося, до формули. Можна було б, аналогічно тому, як це було зроблено вище, знов скористатись формулою Лагранжа з залишковим членом і покласти:

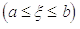
Про інтегрувавши рівність (15), ми не змогли б спростити інтегральний вираз для додаткового члену за допомогою теореми про середнє, бо вираз 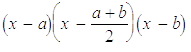в підінтегральній функції вже змінює знак на проміжку 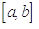. Тому ми зробимо інакше.

Вираз: ,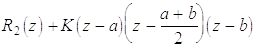

яким би не було число 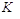, в точках 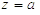, , 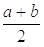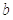приймає одні і ті ж значення, що і функція 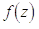. Легко підібрати число 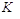так, щоб і похідна цього виразу при 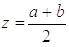співпадала з похідною 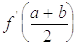. Таким чином, при цьому значенні 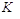ми маємо не що інше, як інтерполяційний многочлен Ерміта, який відповідає простим вузлам 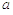, 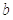і двократному вузлу 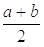. Скориставшись формулою Ерміта з залишковим членом – в припущенні існування для функції 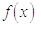похідних до четвертого порядку включно – отримаємо:

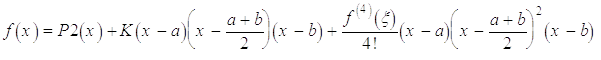
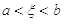Тепер про інтегрувавши цю рівність від 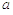до 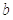; ми знайдемо, що

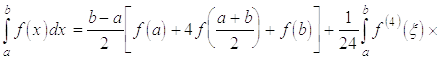
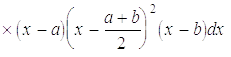
так як .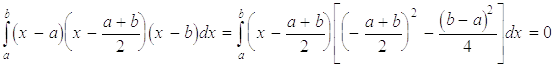

Якщо припустити похідну 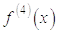неперервною, то, як і в попередніх випадках, залишковий член формули (8)

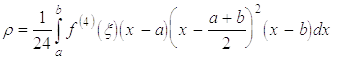користуючись тим, що другий множник в підінтегральному виразі не змінює знак, можна підставити в такому вигляді: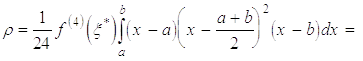

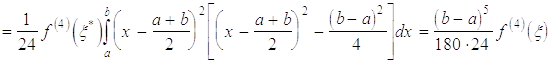Якщо проміжок 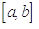розділити на 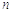рівних частин, то – для формули Сімпсона– отримаємо залишковий член у вигляді 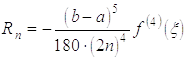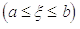.При зростанні 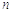цей вираз зменшується приблизно як 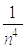; таким чином, формула Сімпсона дійсно більш вигідна, ніж попередні дві формули.
РОЗДІЛ II. СЕРЕДОВИЩЕ ПРОГРАМУВАННЯ ECLIPSE

2.1. Основні характеристики середовища програмування Eclipse

Eclipse (вимовляється «eклі́пс», від англійського «затемнення») — вільне модульне інтегроване середовище розробки програмного забезпечення. Eclipse - один із кращих інструментів Java, створених за останні роки. SDK Eclipse являє собою інтегроване середовище розробки (IDE, Integrated Development Environment) з відкритим вихідним кодом.

На початку свого існування Eclipse з"явилася як комерційний продукт, але в листопаді 2001 р його вихідні коди були опубліковані. Творцем системи є компанія Object Technology International (OTI), яка згодом була придбана корпорацією IBM. Починаючи з 2001 р Eclipse була завантажена більше 50 мільйонів разів і в даний час використовується десятками тисяч програмістів по всьому світу. Підтримкою і розробкою Eclipse в даний час займається організація Eclipse Foundation і спільнота Eclipse, інформацію про яких можна знайти на офіційному сайті в мережі Інтернет http://www.eclipse.org.

Основні інструментальні засоби Eclipse Java включають в себе: редактор вихідного коду (створення і редагування вихідного тексту програм), засоби налагодження і інтеграції з Ant. Крім цього в Eclipse доступні безліч безкоштовних і комерційних доповнень(Плагінів), таких, як інструментальні засоби створення схем UML, розробка баз даних та ін. Власне сама по собі Eclipse - це тільки платформа, яка надає можливість розробляти доповнення, звані плагінами, які природним чином вбудовуються в платформу. В Eclipse доступні доповнення для наступних мов: C та C++, Html, Cobol, Perl, Php, Ruby і ін. Ви можете також розробити власне додаток для розширення можливостей Eclipse.

Eclipse розроблена для широкого кола операційних систем, таких як Linux, Microsoft Windows і Mac OS. Для її запуску потрібно JVM (Java Virtual Machine) - віртуальна Java-машина, а також JDK(Java Development Kit) - набір для Java-розробки. Завантажити дані пакети можна з офіційного сайту розробника Java - http://java.sun.com.

Введення в Eclipse

При первинному знайомстві з середовищем IDE Eclipse вона може здатися дещо складною для непідготовленого користувача. Для того щоб зрозуміти основи роботи з системою, потрібно усвідомити собі основні концепції середовища: робочий простір, інструменти, компонування, редактори та подання.

Робочий простір

У найпростішому випадку робочий простір (workspace) – це каталог для проектів користувача, в якому розташовуються файли проекту. Все, що знаходиться всередині цього каталогу, вважається частиною робочого простору. У нашому посібнику використовуватиметься для прикладів робочий простір: / home / user / workspace.

Інструментальні засоби Eclipse

Інструментальні засоби Eclipse стають доступні відразу після запуску програми. Це по суті сама платформа з набором різних функціональних можливостей головного меню, де колись всього виділяється набір операцій з управління проектом. Фактична обробка, як правило, здійснюється доповненнями (плагінами), наприклад редагування і перегляд файлів проектів здійснюється JDT, і т.д.

До інструментів (workbench) відноситься набір відповідних редакторів і уявлень, розміщених в робочій області Eclipse. Для конкретного завдання визначений набір редакторів і уявлень називають перспективою або компонуванням.

Компонування

Компонування (perspective) - це набір уявлень і редакторів, розташованих в тому порядку, який вам потрібно. В кожній компонуванні присутній свій набір інструментів, деякі компонування можуть мати загальні набори інструментів. У певний момент часу активною може бути лише одна компоновка.

Використовуючи компонування, ви можете налаштувати свій робочий простір під певний тип виконуваного завдання. У посібнику будуть використовуватися компонування, пов"язані в основному з програмуванням на Java, такі, як: Debug, Java Browsing, Java. В Eclipse є також можливість створювати свої компонування. Відкрити компоновку можна командою Window / Open Perspective.

Редактори

Редактори представляють собою програмні засоби, що дозволяють здійснювати операції з файлами (створювати, відкривати, редагувати, зберігати і ін.). уявлення Подання щодо суті є доповненнями до редакторів, де виводиться інформація супроводжувального або додаткового характеру, як правило, про файлі, що знаходиться в редакторі. Відкрити уявлення можна командою Window / Show View. Найбільш часто використовувані уявлення для різних компонувань наведені в табл. 2.

Таблиця 2

Компонування	Представлення
Debug	Breakpoints, Debug, Variables, Expressions, Task, Outline, Console
Java Browsing	Projects, Packages, Types, Members
Java	Package Explorer, Problems, Hierarchy, Outline, Javadoc, Declaration

Проект

Проект (project) являє собою набір файлів програми і супутніх додатків. При роботі з Java використовуються в основному файли, що мають наступні розширення: .java, .jsp, .xml. доповнення Доповненням (plug-in) називають додаток, яке додатково може бути встановлено в Eclipse. Прикладом доповнення може виступати JDT.

Майстри

Майстер - це програмний засіб, який допомагає користувачеві в настройках і проведенні складної операції. В Eclipse є безліч різних майстрів, які роблять роботу користувача в системі зручною і ефективною, беручи частину рутинних операцій на себе. Прикладом майстра може виступити майстер створення нового класу, який допомагає користувачеві в таких операціях, як створення нового файлу в потрібній директорії, створення початкового коду класу, автоматична розстановка модифікаторів і т.д. (Рис. 2.1).

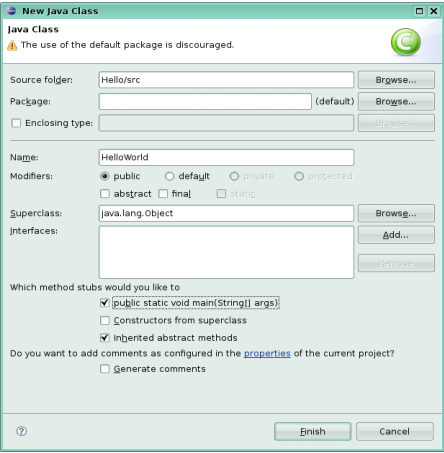
Рис.2.1. Майстер створення нового класу

2.2. Організація роботи в середовищі програмування Eclipse

Для того, щоб приступити до роботи, натисніть кнопку «Workbench». За замовчуванням відкриється універсальний робочий стіл (Рис. 2.2.).

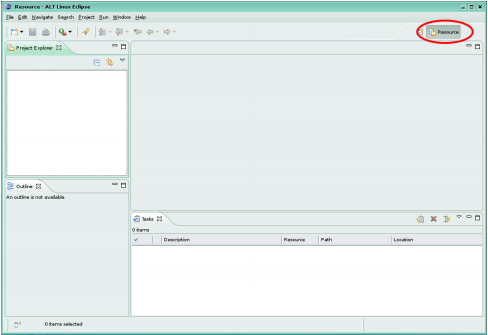
Рис. 2.2. Універсальний робочий стіл

Цей універсальний робочий стіл поки ще не містить в повному обсязі всіх важливих елементів робочого столу Java. На рис. 2.2 виділена мітка, яка відображає поточний режим робочого столу. Для того, щоб переключитися в інший режим, потрібно натиснути кнопку, яка знаходиться зліва від виділеної мітки, і в списку, що розкривається вибрати потрібний режим. На рис. 2.3. можна виділити кілька основних елементів графічного інтерфейсу користувача середовища Eclipse в компонуванні Java.

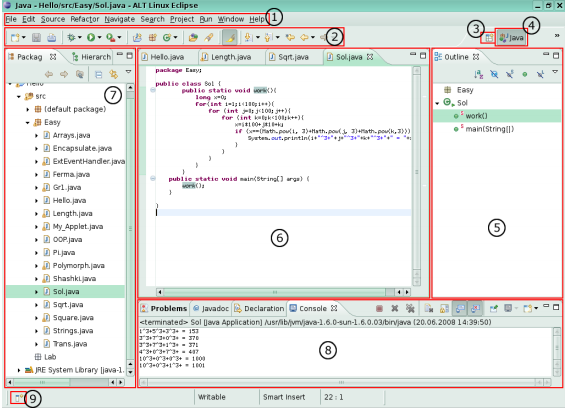
Рис. 2.3. Компонування Java

На рис. 2.4 зображені три основні компонування, які використовуються в роботі над Java-додатками. Кожна компоновка містить свій набір різних панелей і уявлень, а так само їх форму і розташування.

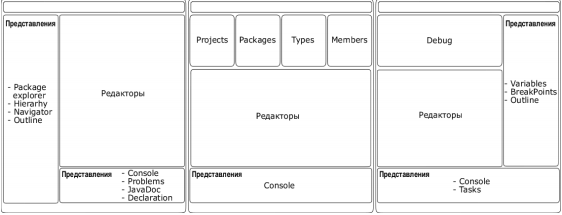
Рис. 2.4. Компонування Java, Java Browsing, Debug

Розглянемо приблизний склад можливих уявлень на прикладі компонування Java. Зразковий склад компонування Java буде наступний.

● Рядок меню (№ 1, Рис. 2.3.). Головне меню платформи Eclipse з набором функцій для роботи з проектами (докладно розглянута в наступному розділі).

● Панель інструментів (№2, Рис. 2.3.).

● Вікно браузера проекту і ієрархії (№ 7, Рис. 2.3.). Призначено для відображення структури робочого простору проекту та є ієрархічну структуру каталогів і файлів, що входять в проект.

● Вікна уявлень (№ 8, Рис. 2.3.). Є 4 основних вкладки:

1) Problems - призначена для відображення помилок при компіляції, а також під час написання програми;

2) Javadoc - відображення коментарів до вибраних об"єктів;

3) Declaration - відображення частини коду, в якому відбувається декларація обраного об"єкта;

4) Console - системна консоль, в яку відбувається висновок

даних програми.

● Перспективи (компонування) (№ 3, Рис. 2.3.)

Дозволяють перемикатися з однієї компонування в іншу. У посібнику будуть використовуватися наступні компонування: Java, Debug і Java Browsing

(Рис. 2.4);

● Редактор коду (№6, Рис. 2.3.)

Призначений для введення і редагування вихідного тексту програм Java.

РОЗДІЛ ІII. ПРОГРАМНА РЕАЛІЗАЦІЯ АЛГОРИТМУ НАБЛИЖЕНОГО ОБЧИСЛЕННЯ ВИЗНАЧЕНОГО ІНТЕГРАЛУ МЕТОДАМИ ПРЯМОКУТНИКІВ, ТРАПЕЦІЙ ТА СІМПСОНА

3.1.Практичне використання алгоритму наближеного обчислення визначеного інтеграла методами прямокутників, трапецій та Сімпсона.

Щоб перевірити правильність обчислення програмного продукту я вирішив вдатись до не ординарного способу перевірки – це Інтернет калькулятор. Ви можете побачити інтерфейс даного Інтернет калькулятора нижче (Рис. 3.1). Даний Інтернет продукт може обчислювати визначні інтеграли трьома способами: прямокутників(Рис. 3.1), трапецій (Рис. 3.2) та Сімпсона(Рис. 3.3).

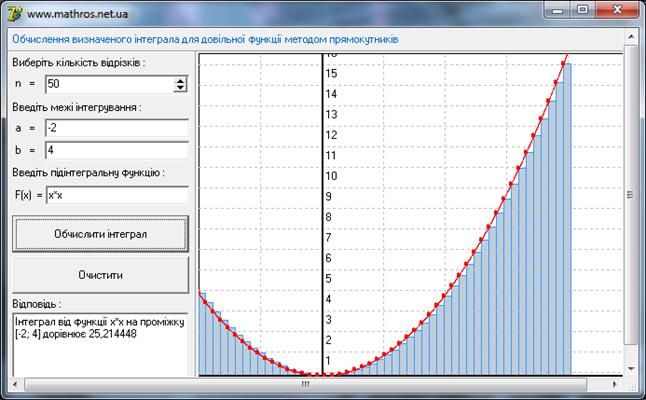
Рис. 3.1 Інтернет калькулятор. Метод прямокутників.

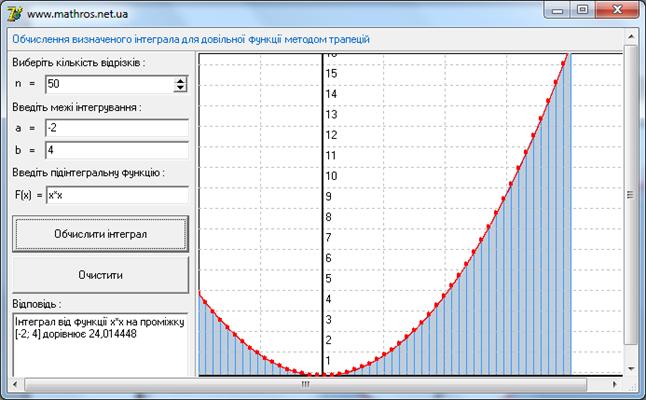
Рис. 3.2 Інтернет калькулятор. Метод трапецій

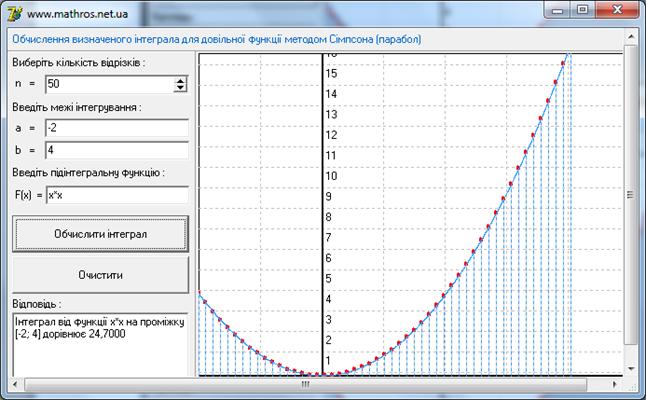
Рис. 3.3 Інтернет калькулятор. Метод Сімпсона.

Вводимо дані для знаходження інтегралу від функції “x^2”(x^2=x*x). Вводимо кількість розбиттів функції, межі інтегрування та обчислюємо значення.

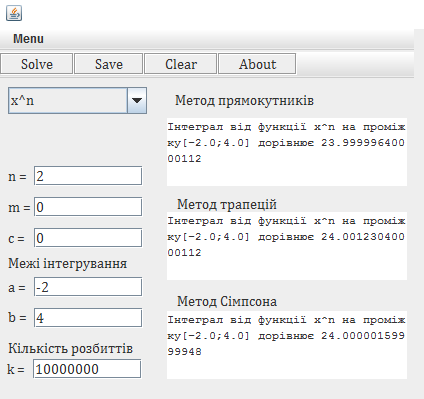
Рис. 3.4 Інтерфейс програмного продукту.

Обчисливши інтеграл від функції можна порівняти отримані значення даного програмного продукту із значеннями отриманими в Інтернет калькуляторі. Хочу зауважити, що дані обчислення є наближеними і залежать від введених даних. Найточніші ж дані дає метод Сімпсона. Зрозуміло, що за менших меж і більшої кількості розбиттів значення будуть точнішими, що я і продемонструю на конкретному прикладі. Знайдемо скінченний інтеграл для функції “k*x” на відрізку [0;3]. Шукане значеня дорівнює 4,5. Можна побачити, що значення в програмному продукті не дорівнюють але прямують до значення 4,5. Найкращий показник тут показали метод трапецій та Сімпсона. Це пояснюється тим що ці методи по своїй побудові найкраще підходить для знаходження інтегралів даного виду. Це видно з Рис 3.5 та Рис. 3.7. Значення Інтернет калькулятора теж не ідеальні і також прямують до шуканого значення (Рис. 3.6 та Рис. 3.8).

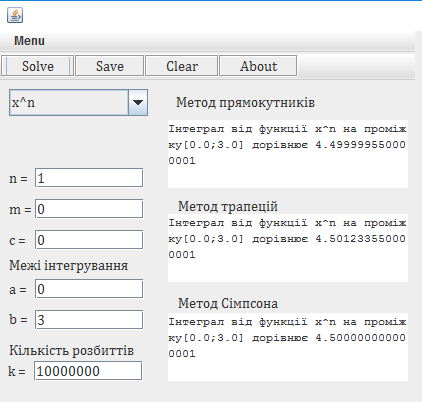
Рис. 3.5 Інтерфейс програмного продукту

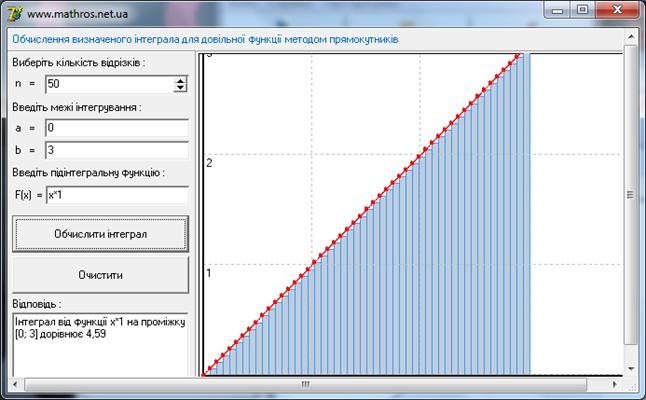
Рис. 3.6 Інтернет калькулятор.

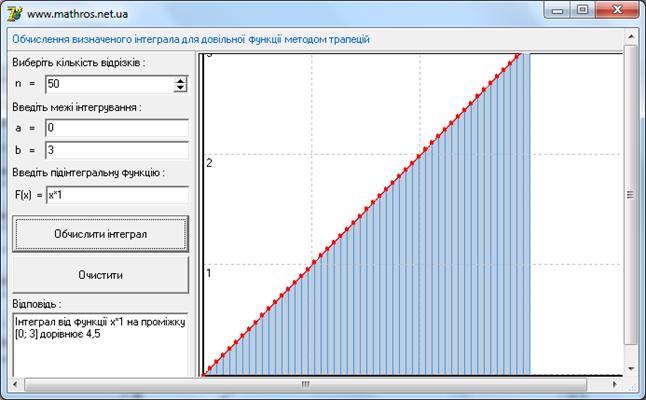
Рис. 3.7 Інтернет калькулятор.

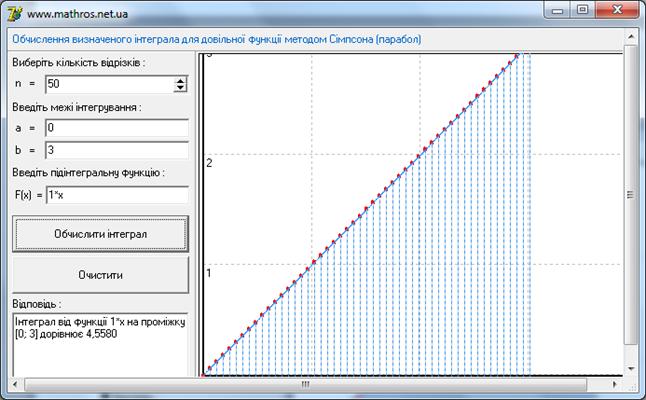
Рис. 3.8 Інтернет калькулятор.

3.2. Опис програмного продукту "Програмування методів чисельного обчислення інтегралів"

Загальний вигляд даного програмного продукту має наступний вигляд Рис 3.9.

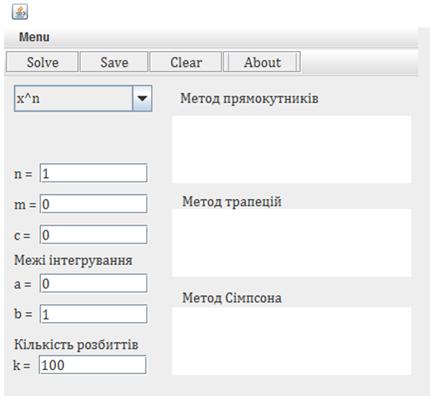
Рис. 3.9 Програмний продукт

Тут передбачено 3 основні функції та 1 додаткову інформаційну. Кожній з них відведено окрему кнопку на інтерфейсі програми. Кожну з них можна викликати нажаттям кнопки. «Solve» - запускає обчислення, «Save» - зберігає відповідь, «Clear» - очищає всі поля, а «About» викликає інформаційне вікно програми. Також деякі з цих кнопок передбачені в меню програми.

Основні елементи які задіяні в обчисленні знаходяться нижче на Рис 3.10.

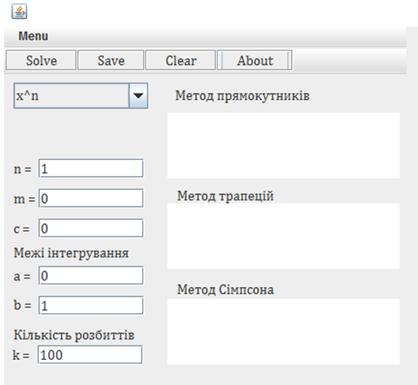
Рис. 3.9 Програмний продукт. Елементи обрахунку

Як ви могли побачити першим елементом є випадаючий список з деяким переліком можливих функцій інтегралів. Далі знаходяться елементи які відповідають за індекси біля тригонометричних функцій, а саме: «n», «m» та «c».

Наступними за ними є елементи що відповідають за межі інтегрування функції та кількість розбиттів, це такі елементи як «a», «b» та «k».

З боку знаходяться текстові поля для виводу інформації про результати інтегрування, кожне з яких підписане і відповідає вказаному методу інтегрування.
В загальному можна сказати, що інтерфейс даної програми інтуїтивно зрозумілий та доступний для будь-кого, хто хоч раз в житті мав справу з визначенням інтегралів.

Висновок:

В даній роботі була зроблена спроба реалізації наближено обчислення визначеного інтеграла методами прямокутників, трапецій та Сімпсона. Було створено програмний продукт, який реалізує ці методи обчислення та відповідна документація до нього. Об’єкт, мета та завдання курсового проекту були виконані.

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

1. Казарин С.А., Клишин А.П. К 143 Среда разработки Java-приложений Eclipse: Учебное пособие – Москва - 2008. — 77 с.

2. Пискунов Н. С. Дифференциальное и интегральное исчисление для ВТУЗов. Т. 1 Москва. - 1968.

3. Воробьева Г. Н., Данилова А. Н. Практикум по численным методам.
Москва. - 1979.

4. Калиткин Н.Н. Численные методы. Главная редакция физико-математической литературы «Наука», Москва. - 1978. – 512 с.

5. Крылов В.И., Бобков В.В. - Монастырский П.И. Вычислительные методы. Главная редакция физико-математической литературы «Наука», Москва. - 1976. – 302 с.

6. Новиков Ф.А. Дискретная математика для программистов. – С.-П. - Питер, 2003. – 292 с.

7. Шендрик Е.В. Конспект лекций по дисциплине «Теория алгоритмов». – Одесса - 2003.