Проектирование кривошипно-ползунного механизма    4

Содержание

Задание                 I   .                                                                   2
1.Синтез, структурное и кинематическое исследование

механизма поршневого двигателя                                              4

1.1.                   Проектирование кривошипно-ползунного механизма    4

1.2.                   Структурное исследование механизма                             4

1.3.                   Построение схемы механизма                                           4

1.4.                   Построение планов скоростей механизма                        5

1.5.                   Построение планов ускорения механизма                        6

1.6.                   Годограф скорости центра масс S2 звена 2                      7

1.7.  Кинематические диаграммы точки В ползуна 3                      8
2.Силовой расчет рычажного механизма двигателя                   9

2.1 .Определение сил давления  на поршень                             9

2.2.Определение сил тяжести звеньев                                        9

2.3.Определение сил инерции звеньев                                       9

2.4.     Силовой расчет звеньев 2 и 3                                               9

2.5.     Силовой расчет входного звена                                          10

2.6.     Силовой расчет по методу Жуковского Н.Е.                     10
3 .Расчет маховика                                                                        
   12

3.1.Построение диаграмм приведенных моментов, работ

и приращений кинетической энергии                                   12

3.2.Построение диаграммы кинетической энергии. Определение момента

инерции маховика!

13

3.3. Определение размеров и массы маховика                                     14

Литература                                                                                    
      16

Задание № 3. Механизм двухтактного

Двигателя внутреннего сгорания.

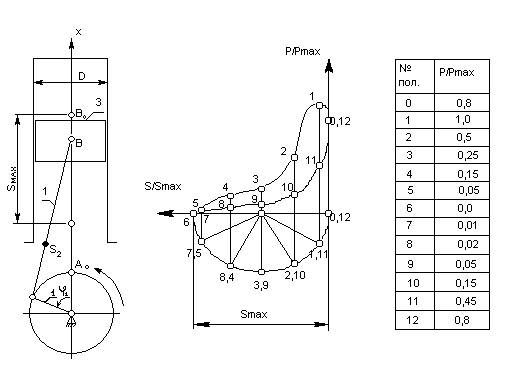
λ=l_AB/l_OA;

m₁=3кг;

AS₂=0,3AB;

P_max=4МПа.

Исходные данные для проектирования и исследования

Механизмов двухтактного двигателя внутреннего

сгорания

Параметр		Обозначение		Величина
		параметра	Единицы СИ
Длина кривошипа ОА		LOA	м	0,04
Угловая          скорость вращения    кривошипа ОА		ω1	С-1	380
Отношение        длины шатуна   АВ   к   длине кривошипа ОА		λ		4,0
Номера       положений механизма для  построения планов ускорений ший ДЛЯ анов				2,5,11
Диаметр поршня		D	М	0,095
Масса кривошипа ОА		m	кг	10
Масса шатуна АВ		m2	кг	3,3
Масса ползуна 3		m3	кг	2,2
Моменты        инерции звеньев   относительно осей,         проходящих через центры масс:		J01 JS2	кгм2  кгм2	0,14 0,025
Максимальное давление .		Pma	МПа	1
Положение механизма для силового расчета
Коэффициент неравномерности движения механизма ма		δ		0,04

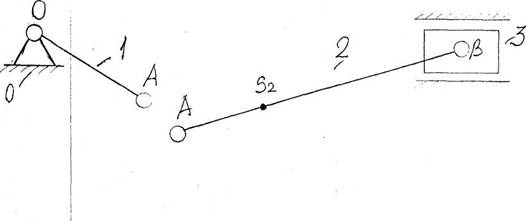
Синтез,    структура    и    кинематическое    исследование    рычажного

механизма.

1.1.Проектирование кривошипно-ползунного механизма.

Определяем длину шатуна АВ

l_AB=λ·l_OA=4,0·0,04=0,16м

1.2.Структурное исследование рычажного механизма

Определяем степень подвижности механизма.

W=3n-2p₅-p₄=3;3-2-4-0=l

где п=3 - число подвижных звеньев

р₅=4 - число кинематических пар пятого класса

р₄=о _ число кинематических пар четвертого класса

Определяем класс и порядок механизма. Он состоит из группы Ассура II

класса, второго вида, второго порядка и механизма I класса, состоящего из

входного звена 1 и стойки 4. в целом рассматриваемый механизм II класса.

1.3.Построение схемы механизма.

Масштаб схемы

μ₁=l_OA/OA=0,04/30=0,001м/мм

Для построения 12 положений звеньев разделим траекторию описываемую т.А кривошипа ОА на 12 равных частей. За нулевое принимаем то положение кривошипа ОА,! при  котором т.В  ползуна  3  занимает  крайнее  верхнее

положение (т.е. начало рабочего хода).

 Из отмеченных на окружности точек

А₀, А_1, А₂…А₁₁ раствором циркуля равным  AB=l_AB/μ₁=0,16/0,001=160мм

Намечаем на линии движения ползуна 3 точки В₀, В₁, В₂…В₁₁. Соединяем прямыми точки  A₀ c B₀, A₁ c B₁ и т.д. Получаем 12 положений звеньев механизма.

1.4Построение планов скоростей механизма.

План скоростей группы Ассура   II класса 2-го вида (звенья 2 и 3)

V_B=V_A+V_BA

где  V_A –скорость т. А кривошипа ОА.

V_A=l_OA·ω₁=0,04·380=15,2 м/с

V_B- скорость т.В ползуна 3, направлена вдоль оси ОВ.

Масштаб планов скоростей

μ_V=V_A/pa=15,2/112,5=0,1(м/с)/мм

Скорость т.S₂ определяем по правилу подобия

as₂/ab=AS₂/AB=> as₂=ab·AS₂/AB=ab·0,3AB/AB=0,3ab.

Истинное значение скорости каждой точки:

V_B=μ_V·pb=0,1·110=11м/с

V_BA=μ_V·ba=0,1·57=5,7м/с

V_S2=μ_V·ps₂=0,1·109=10,9м/с

Определяем угловую скорость шатуна АВ

ω₂=V_BA/l_AB=15,2/0,16=95c^-1

Полученные значения сводим в таблицу 1

Таблица 1

Значения скоростей точек и угловой скорости шатуна АВ механизма.

Пара метр	i Номера положений
	0	1	2	3	4	5	6	7	8	9	10	11
VA	15,2	15,2	15,2	15,2	15,2	15,2	15,2	15,2	15,2	15,2	15,2	15,2
VB	0	9,3	14,9	15,2	11,2	6,0	0	6,0	11,2	15,2	14,9	9,3
VBA	15,2	13,4	6,8	0	6,8	13,4	15,2	13,4	6,8	0	6,8	13,4
VS2	95	83,7	42,5	0	42,5	83,7	95	83,7	42,5	0	42,5	83,7
ω2	10,6	12,2	14,8	15,2	13,7	11,8	10,6	11,8	13,7	15,2	14,8	12,2

1.5.Построение планов ускорений механизма.

Ускорение т.А  звена OA

а_А = ω² · l_0А = 380² · 0,04 = 5776 м/с²                                   Вектор а_A направлен от точки A к точке O. Масштаб планов ускорений

μ_A = a_A/πa=5776/100=57,76 (м/с²)/мм

Строим план звеньев 2 и 3

a_B=a_A+aⁿ_BA+a^r_BA

где а_B - ускорение точки В, направлено вдоль оси X.

aⁿ_BA- нормальное ускорение точки В шатуна АВ, направлено от точки В к точке А вдоль оси АВ.

aⁿ_BA=ω²₂·l_BA=42,5²·0,16=289м/с²

Его масштабная величина равна п_ВА=аⁿ_BA / μ_a=289/57,76=5 мм

a^τ_BA- касательная ускорения т.В шатуна АВ, направлено перпендикулярно оси

АВ.

Ускорение т. S₂ определяем по правилу подобия

as₂ /ab =AS₂/AB=>as₂=ab·AS₂/AB=0,3ab

Численные значения ускорений точек равны

a_B=μ_a·πb=57,76·37=2137 м/с²

a^τ_BA=μ_a·τ_BA=57,76·87=5025 м/с²

a_s2=μ_a·πs₂=57,76·63=3638 м/с²

Определяем угловое ускорение шатуна АВ.

ε₂=a^τ_BA / l_AB=5025/0,16=31406 с^-2

Полученные значения сводим в таблицу 2 .

Таблица 2 Значенияускорений точек иуглового ускоренияшатуна АВ

Параметр	aA	anBA	aτBA	aS2	ab	ε2
2	5776	289	2137	3638	5025	31406
5	5776	1120	4274	2021	2714	26712
11	5776	1120	5718	2021	2714	35737

1.6. Годограф скорости центра масс S звена 2

Соединяем концы векторов ps₂ плавной кривой и получаем годограф скорости t.S₂.

1.7.Кинематические диаграммы ползуна 3.

Диаграмма перемещения. Откладываем по оси абцисс отрезок х=120 мм и делим   его   на   12   равных   частей.   От   точек   1,2,... 11   диаграммы   S(t)

откладываем ординаты 1-1, 2-2,... 11-11, соответственно равные расстояния В₀-В_i,  В₀-В₂, ...В₀-В₁₁. Соединяем полученные точки.

 Масштабы диаграммы

μ_s=μ₁ =0,001 мм.

μ_l=2π / ω₁·x=2·3,14 / 380·180=0,00009 c/мм.

μ_φ=2π / x=2·3,14 / 180=0,034 с/мм.

Диаграмма скорости строится графическим дифференцированием диаграммы

перемещения по методу хорд. Масштаб диаграммы V(t)

μ_V=μ_s / μ_l·H₂=0,001/0,0013·20=0,038 м/с²(мм)

Диаграмма     ускорения     строится     графическим     дифференцированием
диаграммы скорости по методу хорд. Масштаб диаграммы  a(t).

μ_a=μ_V / μ_l·H₂=0,038 / 0,0013·20=1,46 м/с²(мм)

2.Силовой расчет рычажного механизма.

2.1.Определение сил давления газов на поршень

P₃=π·D²/4·P/P_max·P_max=3,14·0,095²/4·0,5·4000000=28338 H

2.2.Определение сил тяжести звеньев.

G₁=m₁·g=3·10=30 H

G₂=m₂·g=3,3·10=33 H

G₃=m₃·g=2,2·10=22 H

2.3. Определение сил инерции звеньев

Ф₂=-т₂ ·a_S2 =3,3·3638= 12005,4 Н

Ф₃=m₃·a_B=2,2·2137= 4701,4 H

M_u2=-I_S2·ε₂ =0,025·13356= 785 Н·м.

Силу Ф₂ прикладываем в t.S₂ , силу Ф₃ прикладываем в т.В и направляем их параллельно и противоположно соответствующим ускорениям.

 Момент от пары сил инерции М_и2 направляем противоположно ускорению ε₂ Производим замену силы инерции F_u2 и момента от пары сил инерции  М_и2 одной результирующей силой Ф"₂. Определяем плечо h"₂.

h^΄₂=M_u2/Ф₂·μ_l=785/12005,4·0,001=65,4мм

2.4. Силовой расчет звеньев 2 и 3

Определяем   величину   реакции   R^τ₂  из суммы моментов всех сил действующих на звено 2,

 ΣM_B(2)=0

R^τ₁₂·AB+Ф₂·h₁+G₂·h=0

R^τ₁₂=Ф₂·h₁+G₂·h₂/AB=12005,4·30+33·184/295=1241 H

Реакции Rⁿ₁₂  и  R₀₂  определим построением силового многоугольника, решая векторное уравнение равновесия звеньев 2 и 3.Rⁿ₁₂+R^τ₁₂+Ф₂+G₂+Ф₃+G₃+P₃+R₀₃=0

μ_P=P₃/P₃=28338/360=78 H/мм

Rⁿ₁₂=μ_P·Rⁿ₁₂=78·295=23010 H

R₁₂=μ_P·R₁₂=78·58=4524 H

R₀₃=μ_P·R₀₃=78·70=5460 H

Определяем реакцию R₃₂, рассматривая равновесие звена 2

R₁₂+G₂+Ф₂+R₃₂=0

μ_P=78 H/мм

R₃₂=μ_P·R₃₂=78·300=23400 H

Расчет группы 2-3 закончим определением плеча h₃.

ΣM_B(2)=R₃·h₃=0

h₃=0, так как R₀₃≠0

2.5 Силовой расчет входного звена.

Из уравнения моментов всех сил относительно т.О определяем уравновешивающую силу P_y

ΣM_O(1)=-P_y·OA+R₁₂·h₄=0

P_y=R₁₂·h₄/OA=4524·72/75=4343 H

Определяем реакцию R₀₁  построением многоугольника сил согласно векторному уравнению звена 1.

P_y+R₂₁+G₁+R₀₁=0

μ_P=R₂₁/R₂₁=4524/250=18 H/мм

R₀₁=μ_P·R₀₁=18·90=1620 H

2.6.Силовой расчет по методу Жуковского Н.Е.

Строим для положения 10 в произвольном масштабе план скоростей повернутый на 90^˚. В одноименные точки плана переносим все внешние силы, действующие на звенья механизма, включая и силу Р_у. Составляем уравнение моментов всех сил относительно полюса P плана скоростей

-P^ж_y·pa+G₂·h₆+Ф₂·h₅+(P₃-Ф₃)·pb+G₃·pb=0

P^ж_y=G₂·h₆+Ф₂·h₅+(P₃-Ф₃)·pb+G₃·pb/pa;

P^ж_y=33·26-12005·14+(28338-4701)·0+22·90/39,3=4346H

Δ=[P_y-P^ж_y]/P_y·100%=4343-4346/4343=0,07%

З.Расчет маховика

З.1 Построение диаграмм приведенных моментов, работ и приращения кинетической энергии.

Определяем    приведенный    к    валу    кривошипа     1     момент    сил сопротивления без учета сил тяжести звеньев.

                                 _ ^ _                  _ ^ _                                                                 

M^C_П=P₃·V_B/ω₁·cos(P_3,V_B), где cos(P,₃V_B)=cos180˚=-1

                                               Cos(P₃,V₃)=cos0˚=1

Полученные значения заносим в таблицу 3 и строим по ним диаграмму

M^C_П=f(φ₁) (1) в масштабе μ_M=[M^C_Пmax]/Y_max=[-512,7]/102,5=5 H·м/мм

Расчетная таблица определения приведенного момента сил давления газов (сопротивления).

№ п/п	P/Pmax	P3,H	VB м/с	_ ^ _ (P3 VB),град	_ ^ _ cos (P3  VB)	MCn H·м
0	0,8	22670	0	0	1	0
1	1,0	28338	9,3	0	1	200
2	0	0	14,9	180	-1	0
3	0	0	15,2	180	-1	0
4	0	0	11,2	180	-1	0
5	0	0	6,0	180	-1	0
6	0	0	0	180	-1	0
7	0,01	283	6,0	180	-1	-5,1
8	0,02	566	11,2	180	-1	-41,7
9	0,05	1416	15,2	180	-1	-161,2
10	0,15	4250	14,9	180	-1	-456,2
11	0,45	22670	9,3	180	-1	-512,7

Масштаб по оси абцисс

μ_φ=2π/x=2·3,14/180=0,03 1/мм

    Методом графического интегрирования диаграммы M^C_n=f(φ₁)  (1)

Строим диаграмму работ движения сил сопротивления А_Д=f(φ₁)   (2)

В масштабе   μ_A=μ_M·μ_φ·H=5·0,034=3,4 Дж/мм

    Соединяя начало и конец диаграммы  А_С=f(φ₁)  (2) прямой линией получим диаграмму работ движения сил А_Д=f(φ₁)  (3).

  Методом графического дифференцирования диаграммы А_Д=f(φ₁)   (3)

Строим диаграмму постоянного движущих сил М^Д_n=f(φ₁)= const   (4)

    Для построения диаграммы приращения кинетической энергии механизма ΔT=f(φ₁) (5)

нужно алгебраически вычесть из ординат диаграммы А_Д=f(φ₁)  (2) ординаты диаграммы

А_С=f(φ₁)  (3). Масштаб полученной диаграммы μ_T=μ_A=3,4 Дж/мм.

3.2. Построение диаграммы кинетической энергии. Определение момента инерции маховика

Определяем кинетическую энергию звеньев второй группы для всех положений механизма.

T=T₂+T₃;

Где T₂=l_S2·ω²₂/2+m_2·V²_S2/2

      T₃=T_3пост=m₃·V²_B/2.

По вычисленным значениям строим диаграмму T_П=f(φ₁)  (6) в масштабе

 μ_Т=1 Дж/мм.

В этом же масштабе на этих же осях перестраиваем диаграмму ΔT΄=f(φ₁)  (5) и будем обозначать её ΔT΄=f(φ₁) (5΄).

    Строим диаграмму (7), показывающую изменение кинетической энергии звеньев первой группы. Для чего из ординат диаграммы ΔТ΄=f(φ₁) (5΄)

Алгебраически вычитаем ординаты графика T_П=f(φ₁) (6)

          К последней диаграмме проводим две горизонтальные прямые, касающиеся точек с минимальной и максимальной ординатами. Полученный таким образом отрезок  АБ определяем максимальное значение кинетической энергии звеньев первой группы.

ΔT_1max=μ_T·(AB)=30·295=8850 Дж

Определяем приведенный момент инерции звеньев первой группы

J_П1=ΔT_max/ω²₁·δ=8850/380²·0,04=1,5 кг·м²

Определяем момент инерции маховика.

J_M=J_П1-J₀₁=1,5-0,14=1,36 кг·м²

3.3.Определуние размеров и массы маховика.

D=0,38  J_M=0,38  1,36 =0,16 м

d=0,15D=0,15·0,16=0,024 м

d₁=0,25D=0,25·0,16=0,04 м

b=0,165D=0,165·0,16=0,026 м

b₁=1,9b=1,9·0.026=0,23 м

m=8·J_M/D²=0,38·1,36/0,23²=1,36 кг

Результаты расчетов маховика.

Таблица 4

№ п/п	Мgm Н·м	Mg/μn мм	Ag/μA мм	AC/μC мм	ΔT/μn мм	TII/μT мм	ΔT
0	0	0	21,5	21,5	0	7,4	-7,4
1	746	37,3	9,7	1,8	7,9	7,4	-4,2
2	596	29,8	22,5	3,6	18,9	12,1	-0,2
3	316	15,8	30,2	5,4	24,8	19,1	5,4
4	157	7,85	34,2	7,2	27	19,4	12,8
5	27	1,35	35,6	9	26,6	14,2	17,4
6	0	0	35,6	10,8	24,8	9,4	13,3
7	-4,6	-0,23	35,3	12,6	22,7	7,4	6,4
8	-17,4	-0,87	35	14,4	21,1	9,4	9,3
9	-70,2	-3,51	34	16,2	17,8	7,4	13,8
10	-195	-9,75	31,7	18	13,7	14,4	17,1
11	-337	-16,85	26	19,8	6,2	12,1	9,3
12	0	0	21,5	21,5	0	7,4	7,4

Литература

1 .Артоболевский И.И. Теория механизмов и машин, М., Наука, 1975. 2.Попов С.А. Курсовое проектирование по теории механизмов и машин, М., Высшая школа, 1996 3.Теория   механизмов   и   машин,   методические   указания   по   изучению

дисциплины и выполнению курсового проекта, М., 1989.

4.Уржунцев И.П. Методические указания к курсовому проектированию по

теории механизмов и машин, Пермь, 1998.