Проблема оптимизации запасов в звеньях цепей поставок является общеизвестной и достаточно
актуальной. Актуальность этой проблемы, несмотря на длительную историю развития данного направления в логистике, обусловлена, в основном, следующими факторами:
- в случае некорректного определения оптимального уровня заказа и оптимального уровня
запасов, содержащихся на складе, возникает либо дефицит товара, либо иммобилизация дополнительных денежных средств в запасах, что в настоящее время недопустимо;
- применение специальных моделей управления запасами (рассмотренных в различных литературных источниках) весьма затруднительно в реальной практической деятельности.
Формат моделей управления запасами обусловливается, в частности, необходимостью учета многих факторов. Среди таких факторов, прежде всего, подчеркнем следующие:
- характер спроса (в общем случае спрос является случайным);
- характер промежутков времени доставки запасов (они также в общем случае - случайные величины);
- особенности стратегии пополнения запасов (с учетом объемов приращения запасов и моментов подачи заказов на такое пополнение);
- особенности критерия оптимизации системы управления запасами (минимизация суммарных годовых затрат; максимизация интенсивности потока доходов и т.д.);
- требования учета временной стоимости денег в рамках таких моделей (учет временной структуры
- действующих на рынке процентных ставок);
- специфика дополнительных атрибутов, которые требуется учитывать в формате оптимизационной модели управления запасами (например, необходимость принятия решений в условиях неопределенности).
Формат такой модели предполагает следующее: спрос на продукцию является постоянным; наличие дефицита продукции недопустимо; известны все параметры модели.
В частности, известно годовое потребление по анализируемой номенклатуре, известны издержки хранения на единицу продукции, известны накладные расходы на каждую поставку (это – издержки, которые не зависят от размера заказа). Кроме того, если не оговорено противное, то принимается, что издержки поставок, которые зависят от размера заказа, при формализации модели учитываются соответственно в стоимости единицы продукции. Оптимизируются: значение размера q заказа при поставках; длительность Т интервала времени между поставками (она связана с размером заказа q равенством Т= q/D ). Традиционное графическое представление модели дает рис. 1.1.
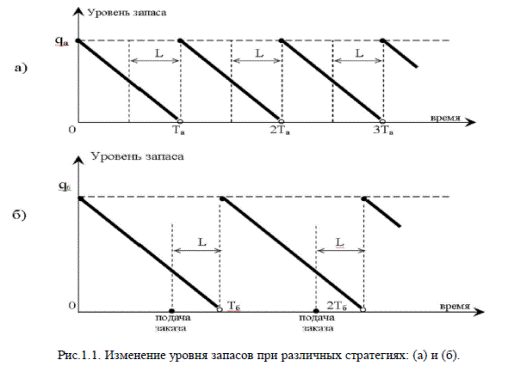
При оптимизации моделей управления запасами одним из наиболее простых и наглядных инструментов является формула Харриса – Уилсона. Ее называют формулой экономичного размера заказа (Economic Order Quantity — EOQ). Формат такой формулы накладывает отмеченные выше требования к модели управления запасами. Предполагается, что известны параметры модели, а спрос считается постоянным. С моделью указанного типа соотносят следующие параметры:

Особенности модели управления запасами в условиях неопределенности с учетом процессов естественной убыли продукции
В рамках теории принятия решений в условиях неопределенности задача выбора наилучших решений должна быть формализована на основе ее представления с помощью матрицы полезностей. Для построения матрицы полезностей менеджеру или лицу, принимающему решение, (далее ЛПР)
необходимо определить:
1. полную группу случайных событий, влияющих на конечный экономический результат;
2. перечень анализируемых альтернативных решений.

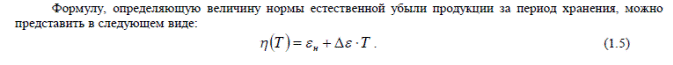


Несоблюдение правил хранения товара, упаковки, нарушение санитарных и




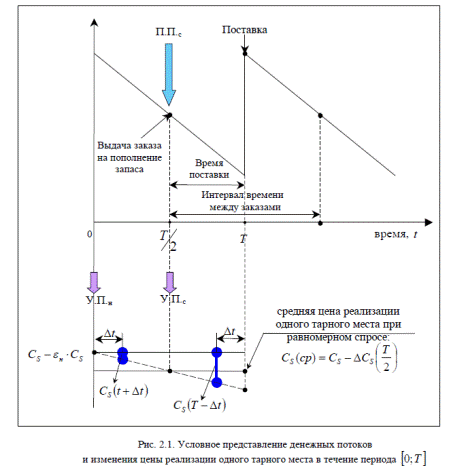
Оптимальный размер заказа, максимизирующий
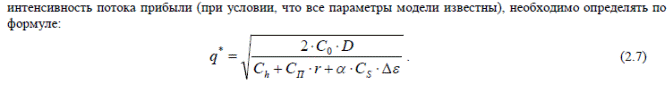














 (zip - application/zip)
(zip - application/zip)










