Департамент образования города Москвы
ГБПОУ КАИТ №20
Реферат по математике
На тему: «Применение комплексных чисел».
Выполнила Cоболева Л.А. группы ТП 232
Проверила
преподаватель Медведева_А.Ю.
Оценка
Комплексные числа используются во многих областях, включая:,электромагнетизм,квантовая физика, применяла
математику, и теорию хаоса. Когда основная область чисел для математической
конструкции - область комплексных чисел
Применение комплексных чисел позволяет перейти от графических преобразований векторных параметров цепей переменного тока к алгебраическим преобразованиям.
Применение комплексных чисел позволяет от геометрического сложения или вычитания векторов на векторной диаграмме перейти к алгебраическому действию над комплексными числами этих векторов.
Применение комплексных чисел позволяет заменить геометрическое суммирование или вычитание векторов токов и напряжений алгебраическим суммированием комплексных чисел, соответствующих этим векторам.
Применение комплексных чисел позволяет от геометрического сложения или вычитания векторов на векторной диаграмме перейти к алгебраическому действию над комплексными числами этих векторов.
Вычисление многих интегралов, относящихся к разряду "неберущихся" (в смысле нахождения первообразных в классе элементарных функций), превращается в почти тривиальную проблему при использовании аппарата теории функций комплексной переменной.
Комплексные числа лежат в основе математического аппарата квантовой физики. Например, ключевое уравнение квантовой механики – уравнение Шрёдингера – содержит мнимую единицу. Решения этого уравнения также включают в себя число i. Однако конечные формулы для расчета наблюдаемых физических характеристик уже не содержат комплексных чисел. Мнимая единица сделала свое дело и скромно удалилась!
В экономике:
Товар является носителем двух составляющих: потребительских свойств, объективно присущих товару, и цены - денежной оценки потребительских свойств товара конкретным потребителем. С учетом того, что и потребительские свойства товара и его цена являются необходимыми показателями свойств товара, возникает потребность разработки и использования комплексного показателя, характеризующего эти две стороны одного объекта. Именно таким показателем может стать комплексное число, состоящее из действительной и мнимой частей.
Представив какую-либо оценку потребительских
свойств товара П как действительную часть комплексного числа, а его цену
Ц - как мнимую часть, получим:
Т = П + iЦ, (1)
где i - мнимая единица, которая определяется условием i? (0, 1) и удовлетворяет соотношению:
i2 = -1. (2)
Легко убедиться в том, что запись (1) позволяет полностью
описать свойства конкретного товара и математически корректно работать как с
каждой из двух его составляющих, так и с их совокупностью в целом.
Для комплексного числа указанная зависимость
наиболее простым способом будет описана так:
(Пи - П) 2 + Ц2= К2 = const. (3)
Действительно, легко убедиться в соответствии с равенством (3), что с уменьшением потребительских свойств товара П (увеличением разности Пи - П) его цена будет уменьшаться, а при повышении потребительских свойств (уменьшением разности Пи - П) и их приближению к свойствам идеального товара цена увеличивается. Так что модель в целом правильно описывает главную особенность потребительской товарной линии.
Воспользовавшись полученной моделью и записью (1), легко описать модель поведения потребителя по отношению к товару как комплексное число:
К = (Пи - П) + iЦ. (4)
В электротехнике:
Описание
электромагнитных процессов в цепях переменного
тока сводится к решению множества интегралов,
а решение их становится столь сложным,
что взять их не пол силу даже
опытным математикам. Определение крайне
упростилось и стало более элегантно при
применении комплексных чисел.
Cинусоидальная форма тока и напряжения
позволяет производить точный расчет электрических цепей с использованием метода
комплексных чисел и приближенный расчет на основе метода векторных диаграмм.
При этом для расчета используются законы Ома и Кирхгофа, но записанные в
векторной или комплексной форме.
|
|
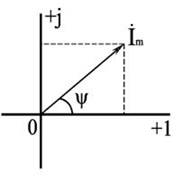
Синусоидальный ток i(t) = Im sin(ωt + ψ) можно представить комплексным числом Ím на комплексной плоскости (рис. 2) Ím = Imejψ, где амплитуда тока Im – модуль, а угол ψ, являющийся начальной фазой, – аргумент комплексного тока. |
Использование комплексной формы представления позволяет заменить геометрические операции над векторами алгебраическими операциями над комплексными числами. В результате этого к анализу цепей переменного тока могут быть применены все методы анализа цепей постоянного тока.
В биологии:
Большое значение комплексных чисел в биологии и ее приложениях широко известно. Они используются в подсчете популяции животных, когда речь идет о конкуренции между разными группами животных. А также при расчётах, решении дифференциальных уравнений, описывающих системы.
В физике:
Описание электромагнитных процессов в цепях переменного тока сводится к решению множества интегралов, а решение их становится столь сложным, что взять их не пол силу даже опытным математикам. Определение крайне упростилось и стало более элегантно при применении комплексных чисел.
Из физики мы знаем, что переменным током называется ток, изменяющийся во времени. Из всех возможных форм периодических токов наибольшее распространение имеет синусоидальный ток.
Любая синусоидальная функция времени a(t) может быть однозначно задана тремя параметрами: амплитудой, частотой и начальной фазой. Ее формула для любого момента времени t:
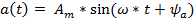 ,
,
где Am — максимальное значение функции или её амплитуда; ω – угловая частота, ψa – начальная фаза (угол функции в момент времени принятый за начало отсчета, т. е. при t = 0), аргумент (ω * t + ψa) называется фаза или фазовый угол, он определяет значение функции a(t) в любой момент времени. В электрических цепях переменного тока синусоидальными функциями времени являются ток, падение напряжения и ЭДС.
Синусоидальная функция времени может быть представлена в виде вращающегося вектора длиной Im с угловой частотой ω. Положение этого вектора в начальный момент времени t = 0 должно составлять угол ψi с осью абсцисс.
Наиболее удобная для проведения расчетов координатная система стала комплексная, так как вектор можно определить четырьмя различными формами записи. Мы рассмотрим алгебраическую форму:
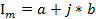 ,
,
надо заметить, что в математике знак мнимой части используется как i, но в электротехнике этим знаком обозначается ток, поэтому было решено заменить его на j. Знак «+» не говорит ни о каком-либо сложении, он только указывает на то, что мы объединяем два действительных числа в нечто единое. На комплексной плоскости a и b координаты конца вектора тока, по мнимой и действительной оси.
Поскольку, гармонический сигнал — это гармонические колебания с течением времени распространяющиеся в пространстве, которые несут в себе информацию или какие-то данные. То, вышеизложенную формулу можно применить к другим объектам и явлениям в физике, которые подвергаются гармоническому (синусоидальному, косинусоидальному) закону (сила упругости, крутильные колебания и т.д.).
Часто используют комплексную запись сигнала:
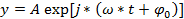
Также применение комплексных функций действительного аргумента позволяет компактно изложить ряд вопросов из области кинематики и динамики.
Пусть точка Z перемещается по плоскости. Выбрав прямоугольную систему координат хОу, можем считать, что движение происходит по комплексной плоскости, а точка Z имеет комплексную координату z = x + i * y, причем x =x(t), y = y(t), z = z(t). В каждый момент времени t точка Z будет иметь определенную скорость u(t), причем ее компоненты равны x(t) и y(t). Следовательно, в каждый момент времени t скорость точки Z характеризуется комплексным числом x(t)+i * y(t), которое можно записать так: z(t). Аналогично ускорение ω точки Z в каждый момент времени t задается комплексным числом:
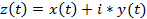
Числа z(t) и z(t) будем называть комплексной скоростью и комплексным ускорением точки Z.
В самолетостроении:
Комплексные числа широко использовал Н. Е. Жуковский (1847 – 1921) при разработке теоремы о подъемной силе. Опубликованная в 1906 г., она сыграла важную роль в развитии теории крыла, которая явилась основой теории летательных аппаратов и получила широкое применение в теории гребных винтов кораблей, а также теории лопастных гидравлических, паровых и газовых турбомашин.
В гидрогазодинамике:
В гидрогазодинамике сложные функции используются, чтобы описать потенциальный поток в
двух измерениях.
В гидрогазодинамике потенциальный поток описывает скоростную область как градиент скалярной функции: скоростной потенциал. В
результате потенциальный поток характеризуется безвихревой скоростной областью,
которая является действительным приближением для нескольких заявлений.
irrotationality потенциального потока происходит из-за завитка градиента, всегда являющегося равным
нолю.В случае несжимаемого потока скоростной потенциал удовлетворяет уравнение Лэплэса.
|
где |
Однако, потенциальные потоки
также использовались, чтобы описатьсжимаемые потоки.
Потенциальный подход потока происходит в моделировании обоих постоянных так же
как нестационарных потоков.Применения потенциального потока например: внешняя
область потока для крыльев, водных волн, и потока грунтовой воды. Для
потоков (или части этого) с сильными эффектами вихрения, потенциальное
приближение потока не применимо
В квантовой механике:
Известно,
что для сохранения инвариантности относительно операции обращения времени, в
квантовой механике необходимо одновременно осуществить комплексное сопряжение:

Этот,
загадочный в квантовой механике, факт на расширенном поле Галуа
становится тривиален.
В качестве простого примера построим комплексное
расширение поля GF(23).Если рассматривать повороты по
часовой стрелке, то на этом поле имеем:
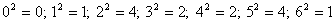
а значит числа
3,5,6 являются квадратичными невычетами. В случае поля Галуа комплексное
расширение можно ввести вполне осмысленно. Для этого достаточно заметить, что
при счете против часовой стрелки ситуация меняется на обратную – числа
1,2,4 становятся квадратичными невычетами, а для чисел 3,5,6 находятся
квадраты.
Таким образом изменение знака времени, изменяющее
направление движения на поле Галуа эквивалентно комплексному сопряжению.
Как мы показали выше, квантовая механика может быть
построена и без комплексных чисел. рассмотрим систему имеющую конечное
множество M локально-связанных состояний.
Комплексность отражает фундаментальное свойство природы -
цикличность фазовой траектории на объективном уровне описания.
Интернет ресурсы:
- http://catalog.studentochka.ru/1606.html комплексные числа и экономика
- http://model.exponenta.ru/electro/0032.htm комплексные числа и электротехника
- http://ru.encydia.com//en/Комплексное_число комплексные числа и все все все
- http://subjphysics.narod.ru/new_page_2.htm комплексные числа и квантовая механика
- http://dict.sernam.ru/
- http://www.webmath.ru/
гарри поттер и комплексные числа














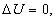
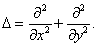
 (zip - application/zip)
(zip - application/zip)










