Преобразование координат. Решение систем линейных уравнений

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования «Вятский государственный университет»

(ФГОУ ВПО «ВятГУ»)

Факультет автоматики и вычислительной техники Кафедра электронных вычислительных машин

________________________________________________________________________________
_______

Реферат по дисциплине Алгебра и геометрия на тему:

«Преобразование координат. Изменение матрицы линейного оператора при переходе к новому базису. Решение систем линейных уравнений»

Выполнил студент группы ИВТ-11______________/Кузнецов А.Н./

Проверил старший преподаватель _______________/Серова А.С./

Киров 2012 г.

Содержание:

I.      Преобразование координат……………………………………………..……….3

1.     Параллельный перенос…………………………………………..….……….3

2.     Поворот вокруг начала координат………………………...……….……….4

II.   Изменение матрицы линейного оператора при переходе к новому базису……………………………………………………………...……………….5

III.             Решение систем линейных уравнений……………………………..…………….6

1.     Решение систем по формулам Крамера…………………………..………...6

2.     Решение систем с помощью обратной матрицы……………..……...……..7

         Список литературы…………………………………………………..……………. 8

I.      Преобразование координат

I.1 Параллельный перенос

Преобразование декартовых прямоугольных координат при параллельном сдвиге осей определяется формулами:

x=x^’+a

y=y^’+b

Здесь ( х,  у) и ( х",  у" ) - координаты произвольной точки Р соответственно в старой и новой системе координат.  Передвинем систему координат XОY в плоскости так, чтобы оси OX и OY оставались параллельны самим себе, а начало координат О сместилось в точку О" ( a, b ). Получим новую систему координат X"O"Y" ( рис.1 )

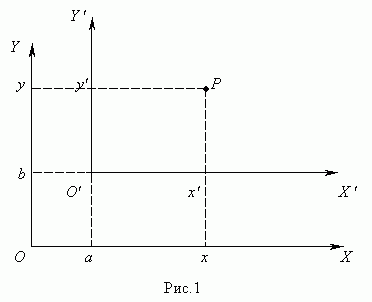
Координаты точки  Р  в новой и старой системе координат связаны соотношениями:

I.2 Поворот вокруг начала координат

Повернём систему координат XОY в плоскости на угол 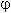( рис.2 )

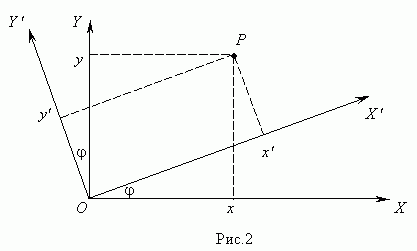
Теперь координаты точки  Р  в новой и старой системе координат связаны соотношениями:

В частном случае 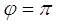   получим центральную симметрию относительно начала координат О :

II.   Изменение матрицы линейного оператора при переходе к новому базису

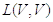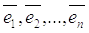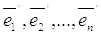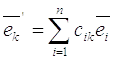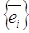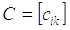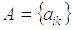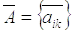Пусть V – линейное пространство, А – линейный оператор из,  и  – два базиса в V и   – формулы перехода от базиса  к базису . Обозначим через   матрицу перехода от базиса к базису. Отметим, что ранг матрицы С равен n. Пусть  и  – матрицы оператора А  в указанных базисах.

Теорема.Матрицы А и 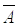 оператора А в базисах 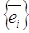 и  связаны соотношением.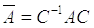

Доказательство. При воздействии линейного оператора А вектор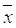  пространства  V переводится в вектор  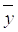 этого пространства, т.е. справедливо равенство

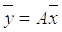                                                (7.3)

(в старом базисе) и равенство

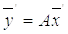                                               (7.4)

(в новом базисе). Так как 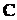 – матрица перехода от старого базиса к новому, то

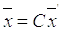                                                 (7.5)

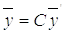                                                (7.6)

Умножим равенство (7.5) слева на матрицу 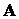, получим  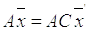и с учетом (7.3) 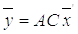. Заменив левую часть полученного выражения в соответствии с (7.6), получим:  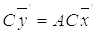 или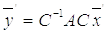. Сравнивая найденное выражение с равенством (7.4), получим доказываемую формулу.

Отсюда следует, что определитель матрицы линейного оператора не зависит от базиса.

III.           Решение систем линейных уравнений

II.1 Решение системы по формулам Крамера

Рассмотрим систему уравнений: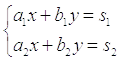

На первом шаге вычислим определитель, его называют главным определителем системы.

 

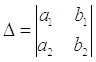
Если 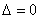, то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.

Если 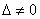, то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:

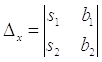  и

Корни уравнения находим по формулам:

,

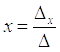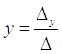
Пример

Решить систему линейных уравнений

 

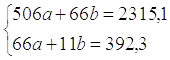
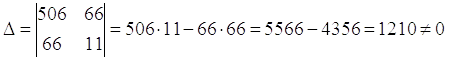
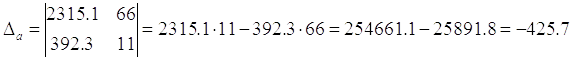
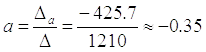
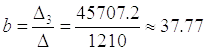
Ответ: ,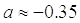 

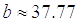
II.2 Решение системы с помощью обратной матрицы

Пример.

Решить систему с матричным методом: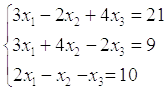 

Решение: Запишем систему в матричной форме:
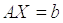, где  ,,

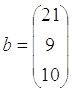
Решение системы найдем по формуле: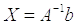

Обратную матрицу найдем по формуле:

, где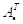  – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы А.

Вычислим определитель  матрицы А:

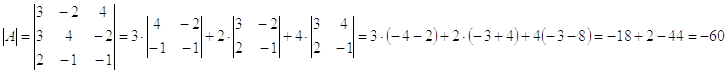Вычислим транспонированную матрицу алгебраических дополнений:

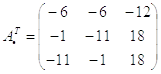
Теперь записываем обратную матрицу:

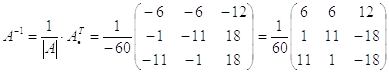
Ответ: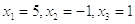           

Список литературы

1)     Сборник задач по аналитической геометрии Д.В. Клетеник 1980г

2)     Сборник задач по математике А.В. Ефимова 2003г

3)     Сборник задач по высшей математике К.Н. Лунгу 2008г