| Министерство сельского хозяйства РФ Государственный университет по землеустройству |
РЕФЕРАТ
ПО ДИСЦИПЛИНЕ: «Физика»
На тему: «Преобразование Лоренца. Интервал между событиями и его инвариантность. Преобразование скорости. Аберрация света.»
| Москва. 2012 г. |
Выполнил: ст. 11 ПГ группы Проверил: преподаватель
Корниенко А. Ю.
Рябов В. А.
Введение
Преобразованиями Лоренца в физике, в частности, в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно-временные координаты каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой. Аналогично, преобразованиям Лоренца при таком переходе подвергаются координаты любого 4-вектора.
Теория относительности опирается на два постулата:
1) Все законы природы одинаковы во всех инерциальных системах отсчета. Как следствие, все инерциальные системы равноправны.
2) Никакими экспериментами невозможно обнаружить абсолютную систему отсчета. Как следствие, скорость света в любой инерциальной системе отсчета постоянна и является «предельной скоростью распространения взаимодействий».
С математической точки зрения преобразования Лоренца — это преобразования, сохраняющие неизменной метрику Минковского, то есть, в частности, последняя сохраняет при них простейший вид при переходе от одной инерциальной системы отсчёта к другой (другими словами преобразования Лоренца — это аналог для метрики Минковского ортогональных преобразований, осуществляющих переход от одного ортонормированного базиса к другому, то есть аналог поворота координатных осей для пространства-времени). В математике или теоретической физике преобразования Лоренца могут относиться к любой размерности пространства.
Преобразования Лоренца
Чтобы явно различить преобразования Лоренца со сдвигами начала отсчёта и без сдвигов, когда это необходимо, говорят о неоднородных и однородных преобразованиях Лоренца. Преобразования Лоренца без сдвигов начала отсчёта образуют группу Лоренца, со сдвигами — группу Пуанкаре, иначе  называемую неоднородной группой Лоренца. Именно преобразования Лоренца, смешивающие — в отличие от преобразований Галилея — пространственные координаты и время, исторически стали основой для формирования концепции единого пространства-времени.
называемую неоднородной группой Лоренца. Именно преобразования Лоренца, смешивающие — в отличие от преобразований Галилея — пространственные координаты и время, исторически стали основой для формирования концепции единого пространства-времени.
Преобразования Лоренца могут быть получены абстрактно, из групповых соображений (в этом случае они получаются с неопределённым ), как обобщение преобразований Галилея.
Преобразования Галилея — в классической механике (механике Ньютона) преобразования координат и времени при переходе от одной инерциальной системы отсчета (ИСО) к другой. Термин был предложен Филиппом Франком в 1909 годуПреобразования Галилея подразумевают одинаковость времени во всех системах отсчета («абсолютное время») и выполнение принципа относительности (принцип относительности Галилея).
Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в пустоте и в ограниченном объёме пространства. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе (и даже бо́льших), преобразования Галилея приближенно верны с очень большой точностью.
Надо заметить, что если не ограничивать класс преобразований координат линейными, то первый закон Ньютона выполняется не только для преобразований Лоренца, а для более широкого класса дробно-линейных преобразований (однако этот более широкий класс преобразований — за исключением, конечно, частного случая преобразований Лоренца — не
Стр.3
сохраняет метрику постоянной).
Специальная теория относительности совпадает с механикой Ньютона либо в мире с бесконечной скоростью света, либо при скоростях, малых по сравнению со скоростью света. Последнее объясняет, каким образом сочетаются эти две теории — первая является обобщением и уточнением второй, а вторая — предельным случаем первой, оставаясь в этом качестве верной приближенно (с некоторой точностью, на практике часто очень и очень высокой) при достаточно малых (по сравнению со скоростью света) скоростях движений.
Преобразования Лоренца сохраняют инвариантным интервал для любой пары событий (точек пространства-времени) — то есть любой пары точек пространства-времени Минковского:
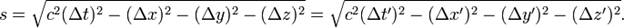
В 1892 году Лоренц ввёл теорию сокращения, предполагающую сокращение длин всех твёрдых тел в направлении движения, количественно совпадающее с тем, что понимается сейчас под лоренцевым сокращением.
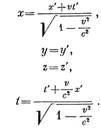
 Преобразования Лоренца были впервые опубликованы Лоренцем в 1904 году, но в то время их форма была несовершенна (они были выведены с точностью до членов V^2 / С^2, а в преобразовании тока была допущена ошибка). К современному, полностью самосогласованному виду их привели французский математик А. Пуанкаре и параллельно и независимо А. Эйнштейн в 1905 году. Анри Пуанкаре первым установил и детально изучил одно из самых важных свойств преобразований Лоренца — их групповую структуру, и показал, что «преобразования Лоренца представляют ничто иное как поворот в пространство четырёх измерений, точки которого имеют координаты »(X, Y, Z, T). В 1905 году Эйнштейн в своей теории относительности пришёл к широко популярной
Преобразования Лоренца были впервые опубликованы Лоренцем в 1904 году, но в то время их форма была несовершенна (они были выведены с точностью до членов V^2 / С^2, а в преобразовании тока была допущена ошибка). К современному, полностью самосогласованному виду их привели французский математик А. Пуанкаре и параллельно и независимо А. Эйнштейн в 1905 году. Анри Пуанкаре первым установил и детально изучил одно из самых важных свойств преобразований Лоренца — их групповую структуру, и показал, что «преобразования Лоренца представляют ничто иное как поворот в пространство четырёх измерений, точки которого имеют координаты »(X, Y, Z, T). В 1905 году Эйнштейн в своей теории относительности пришёл к широко популярной
Стр.4
впоследствии формально-аксиоматической трактовке этих преобразований.
Лоренц-инвариантность — свойство физических законов записываться одинаково во всех инерциальных системах отсчета (с учетом преобразований Лоренца). Принято считать, что этим свойством должны обладать все физические законы, и экспериментальных отклонений от него не обнаружено. Однако некоторые теории пока не удаётся построить так, чтобы выполнялась лоренц-инвариантность.
Инвариант
Понятие инвариантности (инвариантов) в физике лежит в русле принятого в математике понятия «инвариант преобразований (группы преобразований)» (той или иной конкретной группы преобразований — сдвигов времени, преобразований Лоренца и т. п.).
Инвариант в физике — физическая величина, значение которой в некотором физическом процессе не изменяется с течением времени. Примеры: энергия, компоненты импульса и момента импульса в замкнутых системах.
Также инвариантами называются величины, независимые от условий наблюдения, в особенности — от системы отсчета — например интервал в теории относительности инвариантен в этом смысле. Промежуток времени между двумя событиями, а также расстояние между ними (местами событий) для наблюдателей, движущихся в различных направлениях с разными скоростями, будут разными, однако интервал между этими событиями для всех наблюдателей будет один. К этой же категории относится, например скорость света в вакууме. Такие величины, в зависимости от класса систем отсчета, при переходе между которыми сохраняется инвариантность данной величины, называют лоренц-инвариантными (инвариантами группы Лоренца). Или инвариантами группы общекоординатных преобразований (рассматриваемыми в общей теории относительности); для ньютоновской физики может иметь смысл также рассматривать инвариантность относительно преобразований Галилея (инвариантными относительно таких преобразований являются компоненты ускорения и силы).
Стр.5
Аберрация света
Аберрация света (лат. блуждать, уклоняться) — изменение направления распространения света (излучения) при переходе из одной системы отсчёта к другой.
При астрономических наблюдениях аберрация света приводит к изменению положения звёзд на небесной сфере вследствие изменения направления скорости движения Земли. Различают годичную, суточную и вековую аберрации. Годичная аберрация связана с движением Земли вокруг Солнца. Суточная — обусловлена вращением Земли вокруг своей оси. Вековая аберрация учитывает эффект движения солнечной системы вокруг центра Галактики.
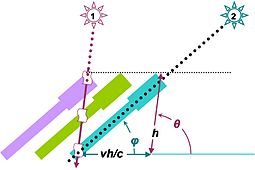
Аберрация света связана с правилом сложения скоростей и имеет простую и наглядную аналогию в обыденной жизни. Предположим, человек с зонтом находится под дождём, капли которого падают вертикально вниз. Если человек побежит с некоторой скоростью, то капли начнут падать под наклоном, ему навстречу. Чтобы не промокнуть человек должен наклонить зонт в направлении движения. Необходимо помнить, что описанная выше ситуация является лишь аналогией световой аберрации. Свет движется существенно быстрее, чем капли дождя. Поэтому для описания аберрации света необходимо пользоваться релятивистским законом сложения скоростей. Скорости света не зависит ни от скорости источника, ни от скорости приёмника.
Аберрация света приводит к изменению положения объекта наблюдения на небесной сфере в результате изменения скорости движения Земли. На самом деле двух наблюдателей, сравнивающих углы в данном случае нет. Наблюдатель один и он расположен на Земле. Второго можно представлять, например, неподвижным относительно Солнца, но как воображаемого. Направление скорости Земли, например, при движении вокруг Солнца меняется. При этом происходит смена сопутствующих к Земле инерциальных систем отсчёта. Поэтому, наблюдатель на Земле через полгода оказывается в системе отсчёта, движущейся в обратную сторону относительно своего прошлого положения. Исключая из аберрационных формул «воображаемого наблюдателя» мы получим изменение угла для астронома в два различных
Стр.6
момента времени. В результате эффекта аберрации звезда в течение года описывает на небесной сфере эллипс (годичная аберрация).
В астрономии используют систему отсчёта, связанную с Солнечной системой, поскольку её с высокой точностью можно считать инерциальной. Звёздные атласы составлены именно в ней, так что эффект вековой аберрации выводится из рассмотрения. Суточная аберрация мала, и даже угол годичной аберрации очень мал; наибольшая его величина — при условии, что движение Земли перпендикулярно направлению луча, — составляет всего около 20,5 секунды. Звезда, находящаяся в полюсе эклиптики и лучи которой перпендикулярны плоскости земной орбиты (практически, эклиптики) в системе отсчёта Солнца, будет в течение всего года наблюдаться отстоящей от своего «истинного» положения на 20,5 секунды, то есть описывать окружность диаметром 41 секунды. Этот кажущийся путь для прочих звёзд уже будет представлять не окружность, а эллипс, у которого большая ось параллельна большой оси эклиптики. Так, если звезда приходится на самой эклиптике, то её годовое движение, вследствие световой аберрации, представится в виде прямой линии, параллельной эклиптике и по этой прямой звезда идёт то в одну сторону, то в другую. Аберрация наблюдается не только для звезд, но и объектов солнечной системы.
 Аберрация света была открыта в 1727 г. английским астрономом Брэдли, который, намереваясь определить параллаксы некоторых неподвижных звёзд, заметил их перемещение. Брэдли объяснял явление аберрации как результат сложения скорости света и скорости наблюдателя. Т. Юнг в 1804 году дал первое волновое объяснение аберрации, как результат действия «эфирного ветра», дующего с равной по величине и обратной по направлению движения наблюдателя скоростью. В 1868 г. Хук поставил опыт, в котором наблюдал земной источник света в телескоп через двухметровый столб воды. В свою очередь Клинкерфус поставил аналогичный опыт с 8-
Аберрация света была открыта в 1727 г. английским астрономом Брэдли, который, намереваясь определить параллаксы некоторых неподвижных звёзд, заметил их перемещение. Брэдли объяснял явление аберрации как результат сложения скорости света и скорости наблюдателя. Т. Юнг в 1804 году дал первое волновое объяснение аберрации, как результат действия «эфирного ветра», дующего с равной по величине и обратной по направлению движения наблюдателя скоростью. В 1868 г. Хук поставил опыт, в котором наблюдал земной источник света в телескоп через двухметровый столб воды. В свою очередь Клинкерфус поставил аналогичный опыт с 8-
Стр.7
дюймовым столбом воды и получил увеличение постоянной аберрации на 7,1" (по его теории ожидалось увеличение на 8"). Для разрешения этого противоречия серию точных опытов провел в 1871—1872 гг. Эйри. Рискуя испортить большой гринвичский телескоп, наполнил его водой и повторил опыт Брэдли по наблюдению звезды γ-Дракона. Он наблюдал звезду вблизи зенита с помощью вертикально установленного телескопа высотой 35,3 дюйма, заполненного водой. По теории Клинкерфуса за полгода угловое смещение звезды должно было составить около 30", в то время как на опыте смещение не превышало 1" и лежало в пределах ошибок эксперимента. Согласно выводам из опыта Эйри следовало — орбитальное движение Земли полностью увлекает светоносную среду.
В 1905 году А. Эйнштейн в первой своей работе «К электродинамике движущихся сред» вывел релятивистскую формулу аберрации.
Преобразование скорости
Преобразования Галилея — в классической механике (механике Ньютона) преобразования координат и времени при переходе от одной инерциальной системы отсчета (ИСО) к другой. Термин был предложен Филиппом Франком в 1909 году. Преобразования Галилея подразумевают одинаковость времени во всех системах отсчета («абсолютное время») и выполнение принципа относительности (принцип относительности Галилея).
Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в пустоте и в ограниченном объёме пространства. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе (и даже больших), преобразования Галилея приближенно верны с очень большой точностью.
Пусть опять система K" движется относительно системы K со скоростью V вдоль оси x. Пусть  x=dx/dt есть компонента скорости в системе K, а
x=dx/dt есть компонента скорости в системе K, а  "x=dx"/dt" — компонента скорости той же частицы в системе K". Мы имеем
"x=dx"/dt" — компонента скорости той же частицы в системе K". Мы имеем
dx = 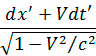 , dy = dy", dz = dz", dt =
, dy = dy", dz = dz", dt = 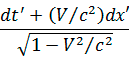 .
.
Стр.8
Разделив первые три равенства на четвертое и введя скорости
v = 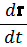 , v" =
, v" = 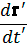 ,
,
находим
 x =
x = 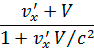 ,
,  y =
y = 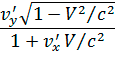 ,
,  z =
z = 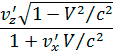 .
.
Эти формулы и определяют преобразование скоростей. Они представляют собой закон сложения скоростей в теории относительности. В предельном случае c→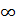 они переходят в формулы классической механики
они переходят в формулы классической механики  x=
x= "x +V,
"x +V,  y=
y= "y,
"y,  z=
z= "z.
"z.
В частном случае движения частицы параллельно оси x имеем  x=
x= ,
,  y=
y= z=0. Тогда
z=0. Тогда  "y=
"y= "z=0, а
"z=0, а  "x=
"x= ", причем
", причем
 =
= 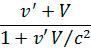 .
.
Легко убедиться в том, что сумма двух скоростей, меньших или равных скорости света, есть снова скорость, не большая скорости света.
Для скоростей V, значительно меньших скорости света (скорость  может быть любой), имеем приближенно с точностью до членов порядка V/c:
может быть любой), имеем приближенно с точностью до членов порядка V/c:
 x =
x =  "x + V
"x + V 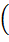 1 −
1 − 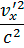
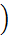 ,
,  y =
y =  "y −
"y −  "x
"x  "y
"y 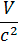 ,
,  z =
z =  "z −
"z −  "x
"x  "z
"z 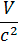 .
.
Эти три формулы можно записать в виде одной векторной формулы
v = v" + V − 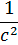 (Vv") v".
(Vv") v".
Стр.9
Заключение
Преобразования Лоренца занимают в теории относительности весьма важное место, составляя одну из ее математических основ. Между прочим, анализ этих формул приводит к доказательству непротиворечивости теории относительности, так что все попытки получить из ее постулатов два противоречащих друг другу следствия заранее обречены на неудачу.
Также заметим, что формулы преобразований Лоренца теряют смысл, если v=c, так как тогда в их знаменателях появляются нули, а деление на нуль, как известно, невозможно. Это значит, что никакие две системы отсчета не могут иметь относительной скорости, равной скорости света. Отсюда вытекает, что и никакое материальное тело не может достичь скорости света, так как ко всякому телу можно «привязать» систему отсчета. Известно, что Эйнштейном разработаны две теории относительности. Целью одной из них, названной Эйнштейном частной или специальной теорией относительности (СТО), является распространение принципа относительности для явлений механики на оптические и электродинамические явления. Целью второй теории, названной общей теорией относительности (ОТО), является распространение принципа относительности на гравитационные явления. В настоящее время обе теории относительности считаются правильными.
Источники
1)http://ru.wikipedia.org/wiki/Инвариант_(физика)
2)http://ru.wikipedia.org/wiki/Преобразования_Лоренца
3)http://ru.wikipedia.org/wiki/Аберрация_света
4) http://n-t.ru/tp/iz/yv.htm
5) http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B5%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F_%D0%93%D0%B0%D0%BB%D0%B8%D0%BB%D0%B5%D1%8F














 (zip - application/zip)
(zip - application/zip)










