Предварительные вычисления в триангуляции

Министерство образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования                                                                  «НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ «ГОРНЫЙ»

Факультет среднего профессионального образования                                                Колледж геодезии и картографии.

КУРСОВАЯ РАБОТА                                                                 по предмету «Высшая геодезия»                                                                       
                  на тему:                                                                                                         «Предварительные вычисления в триангуляции»

        Выполнил:

        Преподаватель: Макеев А.И

Санкт-Петербург

2016 г.

Оглавление

Схема сети............................................................................
.......................................................3

Исходные данные……………………………………………………………………………...4

Таблица 1. Исходные данные………………………………………………………………...4

Цель, содержание и последовательность предварительных вычислений…………………5

Решение треугольников и вычисление сферических избытков…………………………….6

Таблица 2. Решение треугольников и                                                                           вычисл
ение сферических избытков…………………………………………………………..7

Вычисление поправок за центрировку и редукцию…………………………………………8

Таблица 3. Вычисление поправок за центрировку и редукцию…………………………...9

Вычисление приближенных координат…………………………………………………….10

Таблица 4. Вычисление приближенных координат……………………………………….11

Схема хода…………………………………………………………………………………….11

Вычисление поправок за кривизну геодезических линий.                                             Контроль вычисления………………………………………………………………………..12

Таблица 5. Вычисление поправок за кривизну геодезических линий…………………...13

Контроль вычисления поправок за кривизну геодезических линий……………………...13

Приведение измеренных направлений к направлениям на плоскости…………………...14

Таблица 6. Приведение измеренных направлений к                                                   направлениям на плоскости…………………………………………………………………14

Вычисление невязок треугольников сферическим и                                                             плоским направлениям. Оценка точности по невязкам треугольника……………………15

Таблица 7. Вычисление невязок треугольников по                                                      сферическим и плоским направлениям……………………………………………………..16

Вычисление свободных членов полюсных условий……………………………………….17

Таблица 8. Вычисление свободных членов полюсных условий…………………………17

Вычисление рабочих координат…………………………………………………………….18

Таблица 9. Вычисление рабочих координат………………………………………………19

Вычисление превышений и отметок пунктов из                                               тригонометрического нивелирования………………………………………………………20

Таблица 10. Вычисление превышений и отметок пунктов из                      тригонометрического нивелирования………………………………………………………21

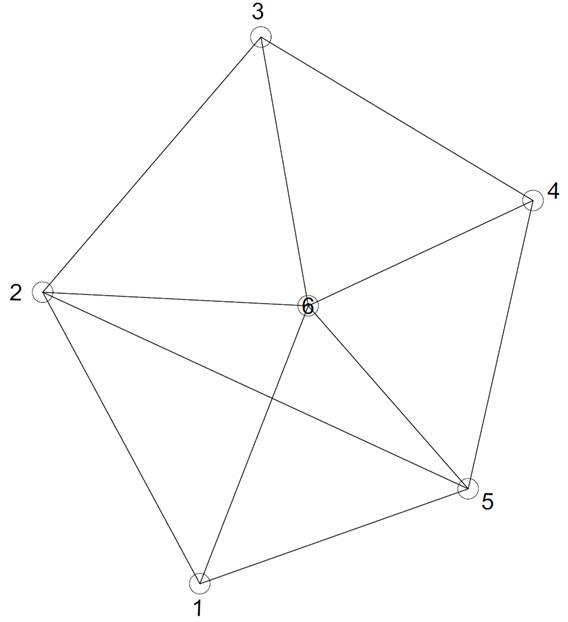
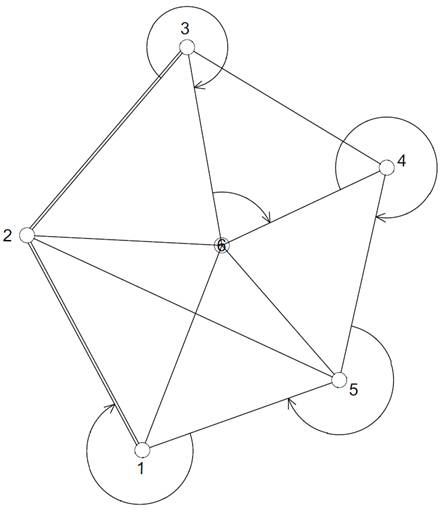
Схема сети.

Исходные данные.

Таблица 1. Исходные данные

№	X, m	Y, m	H, m	Дир. Угол	S, m
1
2
3

ЭЛЕМЕНТЫ ПРИВЕДЕНИЯ
	ЦЕНТРИРОВКИ	РЕДУКЦИИ
№	лин.	угл.	лин.	угл.
1
2
3
4
5
6

ИЗМЕРЕНИЯ
НАПРАВЛЕНИЯ	ЗЕНИТ. РАССТОЯНИЯ
	Пункт №1	V=
1--2		I=
1--6
1--5
	Пункт №2	V=
2--3		I=
2--6
2--5
2--1
	Пункт №3	V=
3--6		I=
3--2
3--4
	Пункт №4	V=
4--5		I=
4--6
4--3
	Пункт №5	V=
5--1		I=
5--2
5--6
5--4
	Пункт №6	V=
6--1		I=
6--2
6--3
6--4
6--5

Цель, содержание и последовательность предварительных вычислений.

 Цель предварительных вычислений в триангуляции - это получение предварительных координат и высот пунктов для дальнейшего сгущения сети и выполнения топографических съемок.

Приближенные вычисления выполняют на основе исходных данных, подготовленных еще до начала работ на вновь создаваемом объекте сети. Такими исходными данными являются координаты Гаусса (плоские прямоугольные) пунктов и редуцированная на плоскость длина базисной стороны или длины сторон треугольников триангуляции высшего класса и их дирекционные углы.

Предварительные вычисления в триангуляции можно разделить на две части. Первая часть, выполняемая при обработке первичных документов (полевых журналов), и вторая часть - это основные предварительны вычисления. Основные предварительные вычисления выполняют в настоящее время на электронно-вычислительных машинах. В этих вычислениях выполняют следующее:

• Решение треугольников и вычисление сферических избытков.

• Вычисление поправок за центрировку и редукцию.

• Вычисление приближенных координат.

• Вычисление поправок за кривизну геодезических линий. Контроль вычисления поправок.

• Приведение измеренных направлений к центрам пункта на плоскости.

• Вычисление невязок треугольников по сферическим направлениям и плоским направлениям.

• Оценка точности сети по невязкам треугольников.

• Вычисление свободных членов полюсных условий.

• Вычисление рабочих координат.

• Вычисление превышений и отметок пунктов из тригонометрического нивелирования.

Решение треугольников и вычисление сферических избытков.

Предварительное решение треугольников в триангуляции выполняется с целью определения неизвестных длин линий, с точностью до целых метров от известной исходной стороны по теореме синусов:

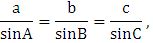
где а, b, с - стороны треугольника;  А, В, С - противолежащие им углы.

При решении сначала записывается вершина, лежащая против известной стороны, затем вершина против промежуточной стороны, т. е стороны, которая не используется в решении следующего треугольника, третья сторона против связующей стороны. При этом используются значения измеренных углов с точностью до десятков секунд и составляющих в сумме в каждом из треугольников  180°(±20”). Полученные длины сторон в дальнейшем необходимы для вычисления поправок за центрировку и редукцию и введения их в измеренные направления. Кроме того, длины сторон используются для вычисления сферических избытков ε" в каждом из треугольников с целью получения их невязок, по которым можно оценить качество измерений.

Сферический избыток треугольника зависит от его площади и вычисляется по любым двум сторонам и углу между ними:

ε"=f*a*b*sin C,

где f=ρ/2R²=0,0253”/км², где ρ" = 206265"; R - средний радиус кривизны поверхности земного эллипсоида, выраженный в километрах, зависящий от широты места.

Значения сторон в формуле выражают в километрах до сотых долей.

Таблица 2. Решение треугольников и вычисление сферических избытков

Вычисление поправок за центрировку и редукцию.

Вычисление поправок за центрировку и редукцию необходимо для приведения направлений к центрам знаков – получения сферических направлений.

Несовпадение проекции центра теодолита с центром знака называется центрировкой. Если при измерении горизонтальных направлений теодолит был установлен не над центром знака, то в измеренные направления вводят исправления, называемые поправками за центрировку. Их величину подсчитывают по формуле:

C”= ,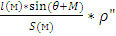

где l - линейный элемент центрировки - расстояние между проекциями на    горизонтальную плоскость вертикальной оси теодолита и центра знака;                             ϴ - угловой элемент центрировки, измеряемый с точностью 15’ от направления на центр знака по ходу часовой стрелки до направления на начальный пункт;                                 М - направление на наблюдаемый пункт, измеренное и приведенное к общему нулю;                                                                                 
                                                    S - расстояние в метрах до наблюдаемого пункта.

Несовпадение центра визирной цели с центром знака называется редукцией. При наблюдении на визирные цилиндры, у которых проекция оси отклоняется от центра знака на величину l₁, в измеренные направления вводят поправки за редукцию. Их величину подсчитывают по формуле:

r”= ,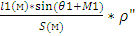

где  l₁ - линейный элемент редукции - расстояние между проекциями центра знака и визирной оси;                                                                                 
                                                      ϴ₁ - угловой элемент редукции, отсчитываемый по ходу часовой стрелки от направления на центр знака до начального направления с точностью 15’;                                                      М₁ - направление на наблюдаемый пункт, измеренное и приведенное к общему нулю;                                                                                 
                                                   S - расстояние до наблюдаемого пункта.

Значения центрировки и редукции вычисляются до сотых долей секунды.

Таблица 3. Вычисление поправок за центрировку и редукцию

Направление	Измеренное направление	M+ϴ	M1+ϴ1	S	c"	r"
1	l=	ϴ=	ϴ1=	l1=
2
6
5
2	l=	ϴ=	ϴ1=	l1=
3
6
5
1
3	l=	ϴ=	ϴ1=	l1=
6
2
4
4	l=	ϴ=	ϴ1=	l1=
5
6
3
5	l=	ϴ=	ϴ1=	l1=
1
2
6
4
6	l=	ϴ=	ϴ1=	l1=
1
2
3
4
5

Вычисление приближенных координат.

При редуцировании угловых измерений на плоскость в проекции Гаусса необходимо в направления, приведенные к центрам пунктов, ввести поправки за кривизну изображения геодезических линий на плоскости. Для получения их значений используются координаты всех пунктов сети, которые нужно знать с точностью до целых метров. Вычисление приближенных координат производят по типу вычисления теодолитного хода.

Выбираем линию хода, проходящую через все определяемые пункты. Выписываем левые по ходу углы и длины сторон хода,  вычисляем дирекционные углы по формулам:

α_след=α_пред+β_лев-180°

α_след=α_предβ_прав+180°

Считаем угловую невязку по формулам:

Ʃβ_теор=α_кон-α_нач+180°*n, где n – число углов в ходе (для левых углов).

Ʃβ_теор=α_нач-α_кон+180°*n, где n – число углов в ходе (для правых углов).

Считаем сумму измеренных углов (Ʃβ_практ).

Приращения координат вычисляем по формулам:

Δx=S*cos α

Δy=S*sin α

Вычисляем координаты пунктов по формулам:

X_след=X_пред+ Δx

Y_след=Y_пред+ Δy

Вычисляем суммы приращений по X и Y:

ΣΔx_практ=Δx₁+…+ Δx_n

ΣΔy_практ=Δy₁+…+ Δy_n

ΣΔx_теор=X_нач-X_кон

ΣΔy_теор=Y_нач- Y_кон

 

 

Таблица 4. Вычисление приближенных координат

№ т. хода	β	α	S	Приращения	Координаты
Δx	Δy	X	Y
3
2
6
4
5
1
2

Схема хода

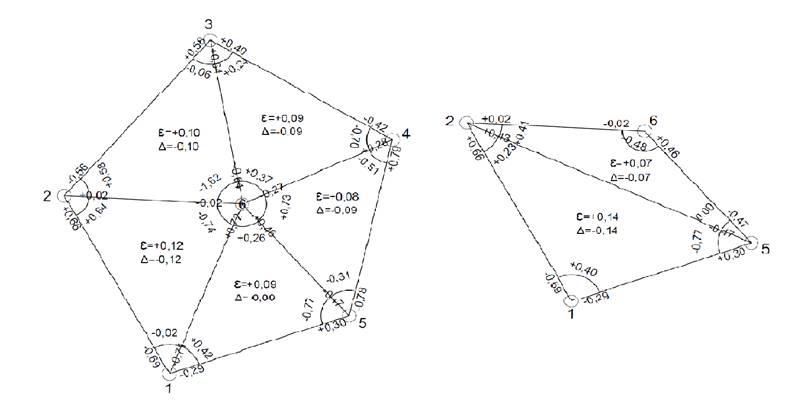
Вычисление поправок за кривизну геодезических линий. Контроль вычисления.

Поправки в направления за кривизну изображения геодезических линий на плоскости в проекции Гаусса-Крюгера для сетей, соответствующих по точности угловых измерений в триангуляции 2-3 классов, вычисляются по следующим формулам:

δ_1-2=1/3f*(X₁-X₂)*(2Y₁+Y₂);

δ_1-2=-1/3f*(X₁-X₂)*(2Y₂+Y₁), где

1, 2 – наименование направлений соответствующих наблюдаемых пунктов сети;                                               X, Y – координаты пунктов сети, выраженные в километрах;                                                           f=0,00253”/км²

При вычислении поправок δ_1-2, δ_1-2 необходимо обратить внимание на значения ординат (Y), данных в условной системе. Для получения их истинных значений необходимо исключить номер зоны и вычесть постоянную величину, равную 500 км, вводимую в ординату для исключения отрицательных значений.

Контроль вычислений поправок производят по сферическим избыткам треугольников и вычисленным поправкам в углы треугольников. Вершины треугольников нумеруются по ходу часовой стрелки. В этом случае поправки в углы при соответствующих вершинах находятся как разности поправок правого и левого направлений. Сумма поправок в углы треугольника должна быть равна сферическому избытку, взятому с обратным знаком, то есть Ʃδ=-ε.

    Таблица 5. Вычисление поправок за кривизну геодезических линий

Формула	1--2	1--5	5--4	4--3	2--3	5--2	6--1	6--5	6--4	6--3	6--2
X1
X2
X1-X2
Y1
Y2
2Y1
2Y2
1/3f	0,0008433
δ1-2
δ2-1

 

Контроль вычисления поправок за кривизну геодезических линий

Приведение измеренных направлений к направлениям на плоскости.

Полученные значения поправки со своими знаками вводятся в исходные направления, приведенные к центрам пунктов. Результатом вычислений является сводка измеренных направлений на плоскости в проекции Гаусса-Крюгера. Сводка редуцированных на плоскости направлений является исходным материалом для уравнительных вычислений и оценки качества выполненных измерений по значениям свободных членов, возникающих в сети, условных координат.

Таблица 6. Приведение измеренных направлений к направлениям на плоскости

Вычисление невязок треугольников сферическим и плоским направлениям. Оценка точности по невязкам треугольника.

Если в измеренные направления ввести поправки за центрировку и редукцию (в нашем случае), то это будут сферические направления, приведенные к центрам знаков. По сферическим направлениям вычисляют сферические углы треугольников и составляют таблицу невязок по сферическим и одновременно по плоским направлениям.

Оценка точности сети по невязкам треугольников производится по формуле Ферреро:

m=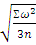, где n – число невязок

Таблица 7. Вычисление невязок треугольников сферическим и плоским направлениям

Вычисление свободных членов полюсных условий.

Полюсные условия возникают в центральных системах и в геодезических четырехугольниках. В первом случае за полюс принимали общую вершину треугольников, во втором случае точку пересечения диагоналей или любую другую вершину, ближайшую к пересечению.

Полюсные условия выражают требования, что любая сторона, вычисленная от другой стороны, должна получить одно и то же значение.

Полюсное условие составляется через отношение сторон и противолежащих им углов. Выбрав за начало одну из обозначенных сторон от пересечения диагоналей составляют их отношение как каждой последующей стороны к предыдущей.

Если прологарифмировать формулу отношения синусов и взять вместо приведенных углов редуцированные, то полюсные условия вычисляются через логарифмы.

Допустимая невязка вычисляется по формуле:

μ=2,5*m*,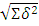                                                                               
                                                                                 
           где δ – изменение логарифма синуса угла при изменении угла на 1”

Таблица 8. Вычисление свободных членов полюсных условий

№ угла	Редуцированные углы	lg sinβ	δ	№ угла	Редуцированные углы	lg sinβ	δ
6-2-3
6-3-4
6-4-5
6-5-1
6-1-2
	Σδ =	2,5*1,5*  =	Σδ =
5-2-6
1-6-5
2-5-1
6-1-2
	Σδ =	2,5*1,5*  =	Σδ =

Вычисление рабочих координат.

Часто съемочные работы производят до окончания триангуляции, в результате которого пункты ее получают окончательные координаты. В таких случаях возникает необходимость вычислить приближенные, так называемые «рабочие координаты», точность которых позволяет на их основе поставить съемочные работы. Рабочие координаты вычисляют с точностью 0,1 м по плоским углам, округленным до 0,1”, исправленным за невязки условий фигур треугольников, с использованием шестизначных таблиц.

Вычисление рабочих координат производят методом последовательной вставки с использованием формул Юнга (котангенсов улов):

x₆=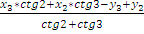

y₆=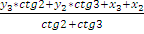

Применяя эти формулы, нужно обязательно нумеровать вершины треугольников против хода часовой стрелки, и пункту, координаты которого вычисляют из данного треугольника, придать номер 3

Таблица 9. Вычисление рабочих координат

Вычисление превышений и отметок пунктов из тригонометрического нивелирования.

Превышения определяют методом тригонометрического нивелирования по формуле:

h=S * ctgZ + 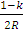*S²(км) + I – V,                                                                              
                                                                      

где: S – расстояние между пунктами                                                                                                                                               Z – зенитное расстояние                                                                      
                                                                                 
            k – коэффициент земного преломления в зависимости от подстилающей поверхности рельефа, он колеблется в пределах 0,14-0,20                                                                            
                                                                         i – высота прибора                                                                         
                                                                                 
               V – высота визирной цели 

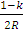=0,0675

Из прямого превышения и обратного  вычисляют среднее значение и берут знак прямого. Расхождение между прямым и обратным превышением не должно быть более 1 м, если стороны не превышает 10 км, если сторона больше 10 км, допуск 0,1 от километров.

Вычисления производятся последовательно. Каждый пункт определяется с трех других и вычисляется среднее значение высоты.

Таблица 10. Вычисление превышений и отметок пунктов из тригонометрического нивелирования

Пункты	i	v	Z	S(м)	h=S*ctgZ	c*S2(км)	i-v	h1-2	h2-1	hср	H	P
1
6
5
2
6
5
3
6
4
4
5
6
3
5
1
2
6
4
6
1
2
3
4
5