Потенциал ионизации. Приближение замороженных орбиталей.

 «Новосибирский национальный исследовательский государственный университет»

Факультет естественных наук

Кафедра неорганической химии Институт Неорганической химии СО РАН

Реферат на тему:

Потенциал ионизации. Приближение замороженных орбиталей.

Теорема Купманса. конфигурационные взаимодейстия

Подготовил:

Студент группы 09402

Пушкарев Р.В.

Проверил:

доктор физ.-мат. наук, профессор

Мазалов Л.Н.

Новосибирск – 2012

Одним из наиболее распространённых методов решения уравнения Шредингера является метод Хартри-Фока. Пользуясь этим методом или методом Хартри (приближение свободных электронов) можно рассчитать энергии каждой орбитали. Отличие состоит в том, что в первом случае в качестве оператора энергии взаимодействия электронов используется так называемый Фокиан, который учитывает межэлектронные, кулоновские взаимодействия, в то время как в методе Хартри в качестве оператора энергии используется Гамильтониан.

В результате решения уравнения вида:

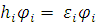 (1),

где 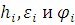 – одноэлектронный гамильтониан, энергия и волновая функция i орбитали соответственно, получается набор орбиталей. Без учета спина картинка расположения энергетических уровней выглядит следующим образом

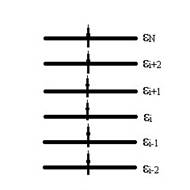
Если удалить с i орбитали электрон:

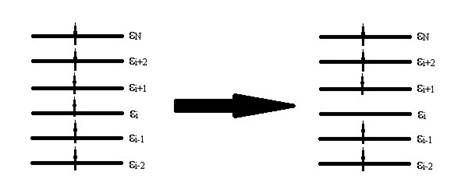
то изменение полной энергии системы (при использовании приближения «замороженных орбиталей») будет равно:

, (2)

Эту величину принято обозначать I – потенциал ионизации. Уравнение (2) представляет собой запись теоремы Купманса, которая гласит, что потенциал ионизации приближенно равен по абсолютной величине орбитальной энергии электрона, удаленного из молекулы; система орбиталей в целом при этом приближенно сохраняется.

Суть же приближения замороженных орбиталей заключается в том, что при удалении одного электрона из системы, или при действии возбуждения, которое переведет электрон на более высокоэнергетичные свободные орбитали, энергии всех орбиталей останутся прежними, что в случае «честного» решения, конечно, не является верным.

Строго говоря, теорема Купманса верна лишь в том случае, когда функция ХФ рассматриваемой системы частиц имеет вид детерминанта Слейтера.

В [1] рассмотрен достаточно строгий вывод теоремы Купманса с использованием приближения Хартри-Фока. Предполагается, что определен вид орбиталей с помощью метода ХФ. Затем стоится волновая функция системы, лишенной одного электрона:

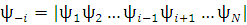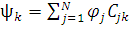, где  (3),

 а 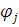 является функцией системы, в которой все электроны находятся на своих орбиталях.

Тогда необходимо найти минимум выражения 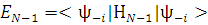, а для этого необходимо определить коэффициенты 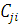. Уравнение для определения этих коэффициентов имеет вид

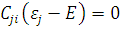 (4)

Можно показать что 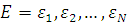, тогда полагая, что

 (5)

Очевидно, что при  обязательно 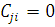, а при 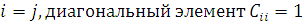, тогда 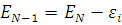. Отсюда, очевидно, следует формулировка теоремы Купманса.

Если не пренебрегать межэлектронным взаимодействием, то для расчета потенциала ионизации в рамках метода ССП уравнение (2) уже не подходит. Необходимо рассчитать энергию системы до и после возбуждения.

 

Интересно, что зачастую, значение потенциала ионизации, рассчитанное с помощью теоремы Купманса, лучше соответствует экспериментальным данным, нежели результат, полученный методом ССП. Вероятно, что это связано с явлением корреляции электронов.

В методе Хартри-Фока оператор Фока подбирается/рассчитывается таким образом, чтобы учесть межэлектронное взаимодействие и в итоге получить самосогласование результатов. Но в этом методе взаимодействие одного электрона с другими представляется, как взаимодействие одного электрона с некоторым усредненным полем, которое создает как ядро, так и остальные электроны. В то же время существует энергия корреляции электронов, которая равна:

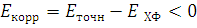
Эта разница возникает вследствие того, что между электронами всегда существует мгновенное кулоновское отталкивание, то есть их движение коррелировано. Различают динамическую корреляцию, связанную с электронным движением и вносящую преобладающий вклад в энергию вблизи точки равновесия системы, и статическую корреляцию, обусловленную невозможностью учета в методе ХФ малых отличий в однодетерминантных волновых функциях, связанных с изменением молекулярной геометрии в ходе химических реакций, при электронных возбуждениях системы.

Разложение N-электронной волновой функции молекулы по набору однодетерминантных волновых функций, описывающих различные электронные конфигурации, является простым и естественным приемом учета электронной корреляции. Каждая электронная конфигурация отвечает вполне определенному набору орбиталей, и в процессе самосогласованного решения уравнений усредненное по конфигурациям межэлектронное взаимодействие охватывает различные варианты распределения электронов при различных расстояниях (r_i-r_j) между ними. В методе конфигурационного взаимодействия многоэлектронная волновая функция раскладывается в ряд по детерминантам Слейтера ψ_k, каждый из которых описывает систему в некотором электронном состоянии. Одно из этих состояний является основным и описывается методом ХФ. Остальные состояния описываются электронными конфигурациями, в которых последовательно учтены возможные переходы электронов с занятых МО на различные незанятые (виртуальные) орбитали. Это означает, что каждый такой детерминант строится из спин-орбиталей, отвечающих основному (ψ₀ = ψ_ХФ) или одному из возбужденных состояний молекулы (ψ_k ≠ ψ₀).

Методы, основанные на одновременном варьировании коэффициентов разложения многоэлектронной функции по конфигурациям a_k и коэффициентов разложения молекулярных орбиталей по базисным функциям (атомным орбиталям) называют многоконфигурационными методами самосогласованного поля. Метод, основанный только на варьировании только коэффициентов a_k, называют методом конфигурационного взаимодействия.

Занятые и виртуальные МО в методе ХФ ортонормированы; соответственно, замещенные детерминанты ортогональны детерминанту основного состояния: .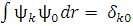

Число замен занятых орбиталей на виртуальные называют кратностью возбуждения.

Важно заметить, что для Хартри-Фоковских орбиталей справедлива теорема Бриллюена: матричные элементы гамильтониана между функцией 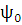 и однократно возбужденными аналогами равны 0, равны 0 так же и матричные элементы между детерминантами, отличающимися тремя и более спин-орбиталями.

Для систем с открытыми электронными оболочками многоэлектронная волновая функция раскладывается в ряд по линейным комбинациям детерминантов Слейтера. Полная волновая КВ-функция, учитывающая все возможные электронные конфигурации, имеет общий вид:

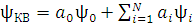 (6)

Формулу (6) можно конкретизировать в зависимости от того, какую кратность возбуждения использует примененный метод конфигурационного взаимодействия. Например, для метода, в котором учитываются одно- и двукратные возбуждения КВ-функция примет вид:

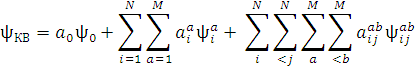
Особое место занимает полное конфигурационное взаимодействие, в котором рассматриваются все возможные возбуждения. На практике же этот метод плохо применим вследствие огромного числа возможных конфигураций при росте количества базисных функций. Поэтому прибегают к сокращению числа конфигураций. Это осуществляют или налагая ограничения на кратность возбуждения, о чем говорилось выше, или в ограничении активного пространства. Во втором случае все орбитали делят на активные и неактивные. Неактивные либо входят во все детерминанты базиса, либо не входят ни в один из них. Остальные орбитали и образуют активное пространство, используемое в методе конфигурационных взаимодействий. Они включают в себя те занятые орбитали, с которых будут проводиться возбуждения, и те виртуальные орбитали, на которые будут попадать возбуждаемые электроны.

Список использованной литературы:

1.     С. Фудзинага «Метод молекулярных орбиталей», 1983 г., М.: Мир

2.     В. Г. Цирельсон «Квантовая химия. Молекулы, молекулярные системы и твердые тела», 2010 г., М.: Бином. Лаборатория знаний

3.     В. И. Барановский «Квантовая механика и квантовая химия», 2008 г., М.: Издательский центр «Академия»