ГОСУДАРСТВЕННОЕ
АВТОНОМНОЕ
ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ЧУВАШСКОЙ РЕСПУБЛИКИ «ЧЕБОКСАРСКИЙ
МАШИНОСТРОИТЕЛЬНЫЙ ТЕХНИКУМ» МИНИСТЕРСТВА ОБРАЗОВАНИЯ И МОЛОДЕЖНОЙ ПОЛИТИКИ
ЧУВАШСКОЙ РЕСПУБЛИКИ
Реферат
На тему «Политропный процесс»
|
Проверил: преподаватель спец.дисциплин Иванова Т.В. |
Выполнила: студентка группы 3М1 Антонова О.В. |
2016г
Содержание:
1. Ведение…………………………………………………………………………………………………………………..2
2. Политропные процессы…………………………………………………………………………………………..3
3. Теплоемкость политропных процессов………………………………………………………………….6
4. Энергетические характеристики политропных процессов…………………………………….8
5. Частные случаи политропных процессов……………………………………………………………….9
6. Обобщенная диаграмма политропных процессов………………………………………………11
7. Пример……………………………………………………………………………………………………………………13
8. Литература………………………………………………………………………………………………………………14
Политропный процесс, политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной.
В
соответствии с сущностью понятия теплоёмкости 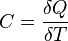 , предельными частными явлениями
политропного процесса являются изотермический
процесс (
, предельными частными явлениями
политропного процесса являются изотермический
процесс (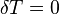 ) и адиабатный
процесс (
) и адиабатный
процесс (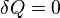 ).
).
В
случае идеального газа, изобарный процесс и изохорный
процесс также являются
политропными (удельные теплоёмкости идеального газа при постоянном объёме и постоянном
давлении соответственно равны 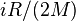 и (
и (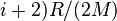 и не
меняются при изменении термодинамических параметров).
и не
меняются при изменении термодинамических параметров).
Политропные процессы
До сих пор рассматривались процессы, у которых имелись вполне определенные признаки: изохорный процесс осуществлялся при постоянном объеме; изобарный — при постоянном давлении; изотермический — при постоянной температуре; адиабатный— при отсутствии теплообмена между рабочим телом и внешней средой. Наряду с этими процессами можно представить еще бесконечное множество процессов, у которых имеются другие постоянные признаки.
Условились всякий процесс идеального газа, в котором удельная теплоемкость является постоянной величиной, называть политропным процессом, а линию процесса — политропой.
Из определения политропного процесса следует, что основные термодинамические процессы — изохорный, изобарный, изотермический и адиабатный,— если они протекают при постоянной удельной теплоемкости, являются частными случаями политропного процесса. Итак, политропный процесс проходит при постоянной теплоемкости.
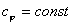
Если теплоемкость зависит от температуры, то нужно найти среднюю теплоемкость, чтобы процесс стал политропным.
Уравнение процесса
Для исследования процесса и расчета слагаемых I закона термодинамики нужно установить связь между параметрами состояния в политропном процессе. Эта функция называется уравнением политропы. Запишем уравнение I закона термодинамики, преобразуем
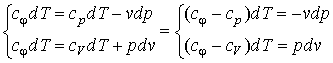
и поделим почленно
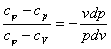
Так как 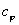 = const в процессе, то левая часть
= const в процессе, то левая часть 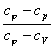 = const и называется показатель политропы:
= const и называется показатель политропы:
n = 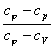 ,
, 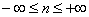
При этом, каждому значению n соответствует некоторый конкретный процесс.
Получили дифференциальное уравнение:
n=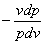
Разделяем переменные
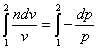
и интегрируем в пределах процесса
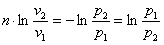
Потенцируем
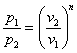 или
или 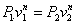
Это выражение выполняется не только для крайних точек процесса, но и для всех промежуточных. Оно называется уравнением политропы:
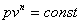
Запишем это уравнение через другие параметры P-T и V-T:
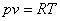
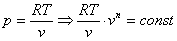
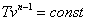
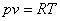
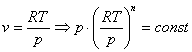
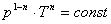
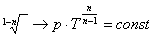

Теплоемкость политропных процессов
Теплоемкость политропного процесса 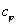 можно
определить из выражения
можно
определить из выражения
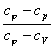 = n
= n
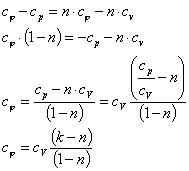
где k - показатель адиабаты.
Найдем значение 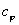 и n для
изопроцессов определения сведем результаты в таблицу
и n для
изопроцессов определения сведем результаты в таблицу
|
процесс |
|
n |
|
T=const |
|
1 |
|
p=const |
|
0 |
|
v=const |
|
|
|
q=const |
0 |
k |
Изобразим зависимость 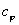 (n)
графически
(n)
графически
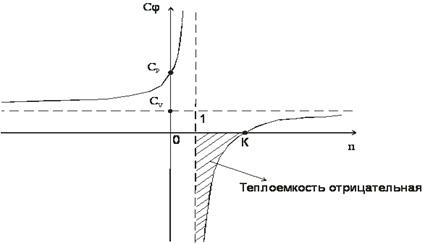
В деапазоне 1<n<k теплоемкость процессов отрицательная, т.е. с подводом теплоты температура системы уменьшается, а с отводом теплоты - увеличивается.
Смысл отрицательной теплоемкости заключается в том, что вся подведенная теплота расходуется на работу и, кроме этого, на работу затрачивается еще и часть внутренней энергии системы
dq=du+dl подвод тепла


|
|
 dq=du+dl отвод тепла
dq=du+dl отвод тепла
Энергетические характеристики политропных процессов
Изменение энтропии
По аналогии с интегралом работы было получено выражение для подсчета количества теплоты в ТДП. Для этого был введен параметр состояния системы – энтропия.
Энтропия является функцией состояния. Ее изменение в пределах процесса определяется как разность конечного и начального значений. Также как внутренняя энергия она определяется с точностью до произвольной постоянной. В ТДП нужно знать только ее изменение. Энтропия, и ее изменение не поддается физическому определению и измерению, а является расчетной величиной.
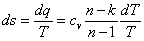
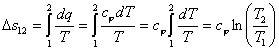
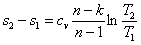
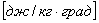
Частные случаи политропных процессов
изобарный Р=const
|
n=0 |
|
|
|
Уравнение процесса |
|
|
|
Теплоемкость |
|
|
|
Изменение энтропии |
|
|
|
Работа расширения |
|
|
|
Количество теплоты |
|
|
|
Изменение внутренней энергии |
|
|
|
Изменение энтальпии |
|
|
|
I закон термодинамики |
|
|
изотермический T=const
|
n=1 |
|
|
|
Уравнение процесса |
|
|
|
Теплоемкость |
|
|
|
Изменение энтропии |
ds=
|
|
|
Работа расширения |
|
|
|
Количество теплоты |
|
|
|
Изменение внутренней энергии |
|
|
|
Изменение энтальпии |
|
|
|
I закон термодинамики |
Вся подведенная теплота идет на совершение работы. |
|
адиабатный dq=0
|
n=k
|
|
|
|
Уравнение процесса |
|
|
|
Теплоемкость |
|
|
|
Изменение энтропии |
ds= |
|
|
Работа расширения |
|
|
|
Количество теплоты |
|
|
|
Изменение внутренней энергии |
|
|
|
Изменение энтальпии |
|
|
|
I закон термодинамики |
Работа совершается за счет внутренней энергии |
|
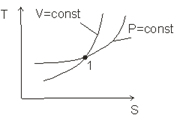
Обобщенная диаграмма политропных процессов.
Для анализа политропных процессов удобно пользоваться обобщенной диаграммой. На ней изображаются все изопроцессы и выделяются области, в пределах которых знаки слагаемых I закона одинаковы.
|
|
||
|
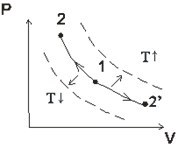
Рабочая диаграмма |
||
|
|
||
|
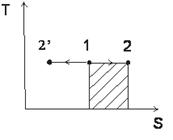
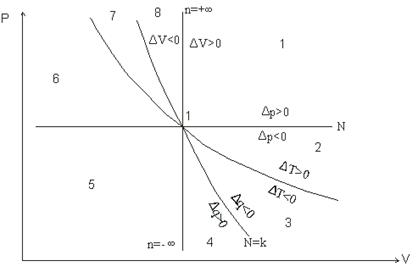
Тепловая диаграмма |
Диаграмма позволяет проанализировать любой политропный процесс и определить условия, при которых этот процесс может быть реализован, то есть, как распределяется теплота между внутренней энергией и работой, что будет с температурой системы и т.д.
- Любой процесс, лежащий выше изобары проведённой через точку 1 сопровождается ростом давления.
- Любой процесс, лежащий выше изотермы сопровождается ростом температуры, внутренней энергии и энтальпии.
- Любой процесс, лежащий правее адиабаты сопровождается ростом энтрапии и подводом теплоты.
- Любой процесс, лежащий правее изохоры идёт с ростом объёма и работа в процессе положительна.
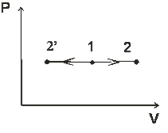
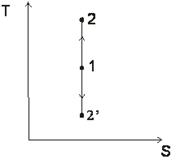
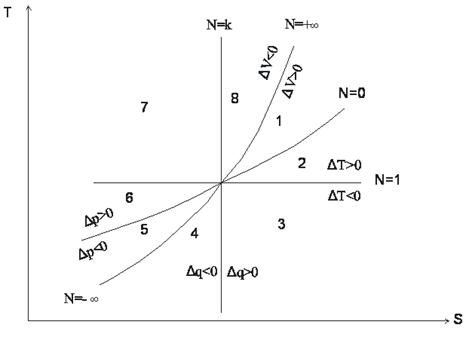
Пример №1:
Изобразить на рабочей диаграмме процесс расширения с отрицательным показателем палитры. Провести анализ этого процесса; найти диапазоны показателей политропы и теплоемкости для таких процессов.
|
|
|
Список литературы:
https://ru.wikipedia.org/wiki/Политропный_процесс
http://tt.pstu.ru/teplot/resource/lection/politrop.htm














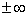
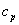
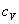
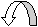
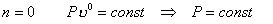 , или
, или 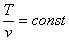
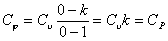
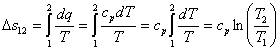
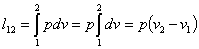
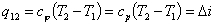
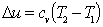
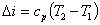
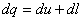
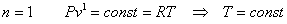
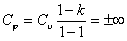
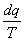 ; q=l (согласно
I закона ТД)
; q=l (согласно
I закона ТД)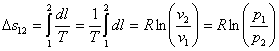
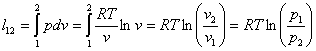
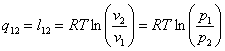
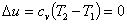
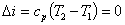
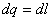
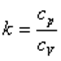

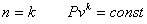 ( уравнение Пуассона).
( уравнение Пуассона).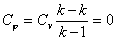
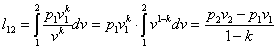
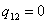
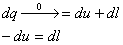
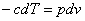
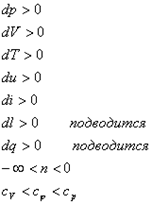
 (zip - application/zip)
(zip - application/zip)










