МиНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
государственное образовательное учреждение высшего образования
«тюменский индустриальныйуниверситет»
Институт транспорта
Кафедра «Сервис автомобилей и технологических машин»
КУРСОВАЯ РАБОТА
по дисциплине
"Технические основы технической эксплуатации ТиТТМО"
|
Выполнил: |
студент гр. АТХб-13-1 Комаров С.В. |
|
Проверил: |
д.т.н., профессор Захаров Н.С |
Тюмень 2016
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ.. 3
ФОРМИРОВАНИЕ СИСТЕМЫ ТЕХНИЧЕСКОГО ОБСЛУЖИВАНИЯ АВТОМОБИЛЕЙ 7
ЗАКЛЮЧЕНИЕ.. 24
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 25
ВВЕДЕНИЕ
Периодичность ТО - это нормативная наработка между двумя последовательно проводимыми однородными работами ТО. Применяются два основных метода проведения технического обслуживания. При первом после достижении определенной наработки изделие восстанавливается до требуемого технического состояния. При втором сначала производится контроль ТСА, затем принимается решение о проведении предупредительных технических воздействий.
Методы определения периодичности ТО подразделяются на:
- простейшие (метод аналогии по прототипу);
- аналитические, основанные на результатах наблюдений и закономерностях ТЭА;
- имитационные, основанные на моделировании случайных процессов.
Рассмотрим наиболее распространенные методы:
· по допустимому уровню безотказности;
· по допустимому значению и закономерности изменения параметра технического состояния;
· технико-экономический метод;
· имитационное моделирование.
Методы определения периодичности ТО
1. По допустимому уровню безотказности. Метод основан на выборе такой рациональной периодичности, при которой вероятность отказа элемента F не превышает заранее заданной величины, называемой риском (рис.1).
Допустимая вероятность безотказной работы принимается для агре- гатов и механизмов, обеспечивающих безопасность движения, Rд = 0,9...0,98, для прочих узлов и агрегатов Rд = 0,85...0,90
Преимущества метода: простота и учет риска
Недостатки метода: неполное использование ресурса изделия.
|
Рис. 1. Метод определения периодичности ТО по допустимому уровню безотказности: |
Rд — допустимая вероятность безотказной работы;
хi — наработка на отказ;
F — риск;
l0 — периодичность ТО.
Определенная таким образом периодичность ТО значительно меньше средней наработки на отказ.
2. По
допустимому значению и закономерности изменения параметра технического
состояния. Изменение параметра Y у группы автомобилей происходит
по-разному (рис. 2). В среднем для этой группы тенденция изменения параметра
характеризуется кривой Y. По этой кривой и допустимому значению
параметра Yg можно определить среднюю наработку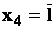 , когда
в среднем вся совокупность изделий достигает допустимого значения параметра
технологического состояния.
, когда
в среднем вся совокупность изделий достигает допустимого значения параметра
технологического состояния.

Рис. 2. Метод определения периодичности ТО по допустимому значению и закономерности изменения параметра технического состояния.
Этойсредней наработке соответствует средняя интенсивность изменения параметра технического состояния. При этом те изделия, у которых интенсивность изменения параметра выше средней (1, 2, 3), достигают предельного состояния значительно раньше. Следовательно, для этих изделий при назначенной периодичностис заданной вероятностью будет зафиксирован отказ.
Подобная система обслуживания нерациональна, поэтому назначают такую периодичность, при которой вероятность отказа не будет превышать заданной величины риска. Этот случай соответствует большей, чем средняя, интенсивности изменения параметра технического состояния, называемой максимально допустимой.
Этот метод применяется для объектов с явно фиксируемым изменением параметра технического состояния. Это большинство изнашиваемых узлов, механизмов, соединений, техническое состояние которых поддерживается с помощью регулировочных работ (тормоза, клапанный механизм и др.).
Преимущества метода: учет фактического технического состояния изделия (диагностика); возможность гарантировать заданный уровень безотказности F; учет вариации технического состояния.
Недостатки метода: отсутствие прямого учета экономичных факторов и последствий; необходимость получить (или иметь)информацию о закономерностях изменения параметров технического состояния.
3. Технико-экономический метод. Метод сводится к определению суммарных затрат на ТО и ремонт и их минимизации. Минимальным затратам соответствует оптимальная периодичность технического обслуживания l0.
Увеличение периодичности ТО, как правило, приводит к сокращению ресурса детали или агрегата и росту удельных затрат на ремонта.
При увеличении периодичности разовые затраты на ТО или остаются постоянными или незначительно возрастают, а удельные затраты значительно сокращаются.
Преимущества метода: учет экономических последствий принимаемых решений (L0); простота, ясность, универсальность.
Недостатки метода: необходимость в достоверной информации о стоимости операции ТО и ремонта, влияния периодичности ТО на ресурс элемента; отсутствие учета вариации (случайность) всех показателей (L, x, d, c); отсутствие гарантии определенного уровня безотказности.
4. Метод определения периодичности ТО с помощьюимитационного моделирования основан на моделировании наработок на отказ и наработок на случай ТО, что позволяет ускорить испытания, уменьшить стоимость экспериментов, рассмотреть несколько возможных вариантов [89]. В качестве исходных данных служат фактические наработки на отказ, а также и законы распределения рассматриваемых случайных величин. Схема моделирования для определения периодичности ТО.
Недостаток метода – при моделировании используется полная выборка наработок на отказ, что на практике не реализуется, т.к. часть отказов предупреждается при проведении профилактических работ. Поэтому целесообразно использовать подходы, использующие методику обработки результатов незавершенных испытаний, к моменту прекращения которых отказывает лишь часть автомобилей, а остальные остаются работоспособными.
ФОРМИРОВАНИЕ СИСТЕМЫ ТЕХНИЧЕСКОГО ОБСЛУЖИВАНИЯ АВТОМОБИЛЕЙ
Исходные данные приведены в таблице 1.
Таблица 1
|
Вариант 54 |
||
|
Выборка |
||
|
1 |
2 |
3 |
|
1,36 |
5,42 |
8,62 |
|
2,13 |
6,68 |
17,25 |
|
1,67 |
8,51 |
19,54 |
|
3,31 |
13,20 |
24,42 |
|
3,90 |
13,73 |
26,39 |
|
3,44 |
21,00 |
29,50 |
|
4,75 |
21,45 |
31,00 |
|
5,26 |
23,47 |
31,79 |
|
6,18 |
23,55 |
32,58 |
|
5,88 |
24,66 |
34,03 |
|
4,87 |
25,92 |
34,41 |
|
5,19 |
27,38 |
34,92 |
|
5,90 |
27,54 |
34,98 |
|
5,37 |
27,83 |
37,57 |
|
7,64 |
28,41 |
38,32 |
|
7,83 |
29,30 |
39,26 |
|
6,86 |
29,34 |
40,65 |
|
6,49 |
30,48 |
41,94 |
|
6,97 |
30,65 |
42,05 |
|
6,90 |
31,24 |
42,59 |
|
7,68 |
32,05 |
43,60 |
|
7,12 |
32,34 |
43,68 |
|
7,35 |
33,12 |
44,52 |
|
7,34 |
33,37 |
44,77 |
|
8,38 |
33,45 |
44,79 |
|
8,88 |
34,44 |
44,84 |
|
8,36 |
34,68 |
46,50 |
|
8,10 |
35,42 |
47,23 |
|
9,41 |
35,62 |
48,25 |
|
8,93 |
35,66 |
48,60 |
|
8,69 |
36,91 |
49,58 |
|
9,25 |
37,57 |
49,59 |
|
9,50 |
37,91 |
49,60 |
|
8,03 |
38,51 |
50,32 |
|
8,93 |
38,66 |
51,26 |
Продолжение таблицы 1
|
8,30 |
38,91 |
52,67 |
|
8,63 |
39,45 |
52,70 |
|
11,07 |
39,45 |
52,76 |
|
10,03 |
40,03 |
52,78 |
|
9,69 |
41,77 |
54,13 |
|
9,88 |
41,90 |
54,36 |
|
10,50 |
41,92 |
55,53 |
|
10,50 |
41,97 |
55,62 |
|
10,79 |
42,23 |
56,22 |
|
10,52 |
42,93 |
56,37 |
|
9,89 |
43,06 |
56,47 |
|
10,47 |
43,58 |
56,51 |
|
10,58 |
44,18 |
56,87 |
|
10,92 |
44,73 |
57,93 |
|
9,75 |
44,92 |
58,86 |
|
9,65 |
44,95 |
59,93 |
|
10,76 |
46,08 |
60,47 |
|
11,26 |
46,19 |
61,04 |
|
11,26 |
46,82 |
61,19 |
|
12,20 |
47,03 |
61,93 |
|
12,48 |
47,42 |
61,99 |
|
11,73 |
47,67 |
62,06 |
|
12,37 |
48,68 |
62,61 |
|
11,21 |
48,69 |
62,74 |
|
11,95 |
49,31 |
65,83 |
|
11,55 |
49,37 |
66,02 |
|
12,36 |
49,81 |
66,03 |
|
12,36 |
51,46 |
66,19 |
|
11,78 |
52,37 |
66,89 |
|
12,20 |
52,53 |
67,08 |
|
11,57 |
52,66 |
67,58 |
|
11,88 |
53,21 |
68,04 |
|
13,19 |
54,13 |
68,48 |
|
13,16 |
54,48 |
68,52 |
|
14,15 |
54,51 |
69,16 |
|
13,56 |
55,02 |
69,17 |
|
13,66 |
55,22 |
69,41 |
|
13,12 |
55,66 |
69,97 |
|
13,79 |
56,48 |
70,99 |
|
13,33 |
57,92 |
72,65 |
|
13,95 |
58,34 |
72,80 |
|
13,84 |
58,53 |
73,34 |
|
13,65 |
58,85 |
73,58 |
|
12,89 |
59,08 |
73,97 |
|
15,03 |
59,40 |
74,27 |
|
14,89 |
59,98 |
74,67 |
|
15,49 |
60,08 |
75,39 |
|
15,06 |
61,80 |
75,53 |
|
Окончание таблицы 1 |
||
|
14,51 |
63,63 |
77,69 |
|
14,80 |
64,86 |
79,07 |
|
14,67 |
65,04 |
79,98 |
|
14,75 |
66,99 |
81,53 |
|
14,62 |
69,24 |
81,76 |
|
17,35 |
69,38 |
82,23 |
|
16,30 |
71,76 |
83,43 |
|
17,39 |
72,70 |
83,45 |
|
16,25 |
72,72 |
84,20 |
|
15,94 |
76,39 |
87,22 |
|
16,79 |
80,98 |
88,06 |
|
17,98 |
81,92 |
92,67 |
|
18,22 |
86,39 |
93,01 |
|
Вероятность безотказной работы |
||
|
0,94 |
0,88 |
|
1. Находятся минимальное значение Xmin и максимальное значение Xmax.
Таблица 2
|
1выборка |
2 выборка |
3 выборка |
|
|
Xmin |
1,36 |
5,42 |
|
|
Xmax |
21,92 |
86,39 |
2. Рассчитывается размах варьирования DX = Xmax - Xmin.
Таблица 3
|
1 выборка |
2 выборка |
3 выборка |
|
|
Xmin |
1,36 |
5,42 |
|
|
Xmax |
21,92 |
86,39 |
|
|
DX |
24,52 |
80,97 |
3. Выстраивается вариационный ряд: Xmin; …; Xmax
Таблица 4
|
Выборка |
||
|
1 |
2 |
3 |
|
1,36 |
5,42 |
8,62 |
|
2,13 |
6,68 |
17,25 |
|
1,67 |
8,51 |
19,54 |
|
3,31 |
13,20 |
24,42 |
|
3,90 |
13,73 |
26,39 |
|
3,44 |
21,00 |
29,50 |
|
4,75 |
21,45 |
31,00 |
|
5,26 |
23,47 |
31,79 |
|
6,18 |
23,55 |
32,58 |
|
5,88 |
24,66 |
34,03 |
|
4,87 |
25,92 |
34,41 |
|
5,19 |
27,38 |
34,92 |
|
5,90 |
27,54 |
34,98 |
|
5,37 |
27,83 |
37,57 |
|
7,64 |
28,41 |
38,32 |
|
7,83 |
29,30 |
39,26 |
|
6,86 |
29,34 |
40,65 |
|
6,49 |
30,48 |
41,94 |
|
6,97 |
30,65 |
42,05 |
|
6,90 |
31,24 |
42,59 |
|
7,68 |
32,05 |
43,60 |
|
7,12 |
32,34 |
43,68 |
|
7,35 |
33,12 |
44,52 |
|
7,34 |
33,37 |
44,77 |
|
8,38 |
33,45 |
44,79 |
|
8,88 |
34,44 |
44,84 |
|
8,36 |
34,68 |
46,50 |
|
8,10 |
35,42 |
47,23 |
|
9,41 |
35,62 |
48,25 |
|
8,93 |
35,66 |
48,60 |
|
8,30 |
36,91 |
49,58 |
|
8,63 |
37,57 |
49,59 |
|
11,07 |
37,91 |
49,60 |
|
10,03 |
38,51 |
50,32 |
|
9,69 |
38,66 |
51,26 |
|
9,88 |
38,91 |
52,67 |
|
10,50 |
39,45 |
52,70 |
|
10,50 |
39,45 |
52,76 |
|
10,79 |
40,03 |
52,78 |
|
10,52 |
41,77 |
54,13 |
|
9,89 |
41,90 |
54,36 |
|
10,47 |
41,92 |
55,53 |
|
10,58 |
41,97 |
55,62 |
|
10,92 |
42,23 |
56,22 |
|
9,75 |
42,93 |
56,37 |
|
9,65 |
43,06 |
56,47 |
|
10,76 |
43,58 |
56,51 |
|
11,26 |
44,18 |
56,87 |
|
11,26 |
44,73 |
57,93 |
|
12,20 |
44,92 |
58,86 |
|
12,48 |
44,95 |
59,93 |
|
11,73 |
46,08 |
60,47 |
|
12,37 |
46,19 |
61,04 |
|
11,21 |
46,82 |
61,19 |
|
11,95 |
47,03 |
61,93 |
|
11,55 |
47,42 |
61,99 |
|
12,36 |
47,67 |
62,06 |
|
12,36 |
48,68 |
62,61 |
|
11,78 |
48,69 |
62,74 |
|
12,20 |
49,31 |
65,83 |
|
11,57 |
49,37 |
66,02 |
|
11,88 |
49,81 |
66,03 |
|
13,19 |
51,46 |
66,19 |
|
13,16 |
52,37 |
66,89 |
|
14,15 |
52,53 |
67,08 |
|
13,56 |
52,66 |
67,58 |
|
13,66 |
53,21 |
68,04 |
|
13,12 |
54,13 |
68,48 |
|
13,79 |
54,48 |
68,52 |
|
13,33 |
54,51 |
69,16 |
|
13,95 |
55,02 |
69,17 |
|
13,84 |
55,22 |
69,41 |
|
13,65 |
55,66 |
69,97 |
|
12,89 |
56,48 |
70,99 |
|
15,03 |
57,92 |
72,65 |
|
14,89 |
58,34 |
72,80 |
|
15,49 |
58,53 |
73,34 |
|
15,06 |
58,85 |
73,58 |
|
14,51 |
59,08 |
73,97 |
|
14,80 |
59,40 |
74,27 |
|
14,67 |
59,98 |
74,67 |
|
14,75 |
60,08 |
75,39 |
|
14,62 |
61,80 |
75,53 |
|
17,35 |
63,63 |
77,69 |
|
16,30 |
64,86 |
79,07 |
|
17,39 |
65,04 |
79,98 |
|
16,25 |
66,99 |
81,53 |
|
15,94 |
69,24 |
81,76 |
|
16,79 |
69,38 |
82,23 |
|
17,98 |
71,76 |
83,43 |
|
18,22 |
72,70 |
83,45 |
4. Определяется количество интервалов:
Nint= Int ( 1 + 3.2 · Log ( N )) .
Таблица 5
|
1 выборка |
2выборка |
3выборка |
|
|
Nint |
7 |
7 |
7 |
5. Рассчитывается длина интервала:
dX= DX / Nint.
Таблица 6
|
1выборка |
2выборка |
3выборка |
|
|
DX |
20,56 |
80,97 |
101,91 |
|
Nint |
7 |
7 |
7 |
|
dX |
24,52012 |
11,57 |
14,56 |
6. Определятся границы интервалов по каждому интервалу (NumInt – номер интервала):
Начало интервала: Xнач= Xmin + dX · ( NumInt - 1);
Конец интервала: Xкон= Xmin + dX · ( NumInt );
Середина интервала: Xсер= Xmin + dX · ( NumInt - 0,5).
Таблица 7
|
Номер интервала |
Выборка |
||
|
1 |
2 |
3 |
|
|
dx |
2,94 |
11,57 |
14,56 |
|
1 Xнач |
1,36 |
5,42 |
8,62 |
|
Xсер |
2,83 |
11,21 |
15,90 |
|
Xкон |
4,30 |
16,99 |
23,18 |
|
2 Xнач |
4,30 |
16,99 |
23,18 |
|
Xсер |
5,76 |
22,77 |
30,46 |
|
Xкон |
7,23 |
28,56 |
37,74 |
|
3 Xнач |
7,23 |
28,56 |
37,74 |
|
Xсер |
8,70 |
34,64 |
45,02 |
|
Xкон |
10,17 |
40,12 |
52,30 |
|
4 Xнач |
10,17 |
40,12 |
52,30 |
|
Xсер |
11,64 |
45,91 |
59,58 |
|
Xкон |
13,11 |
51,69 |
66,85 |
|
5 Xнач |
13,11 |
51,69 |
66,85 |
|
Окончание таблицы 7 |
|||
|
Xсер |
14,57 |
57,48 |
74,13 |
|
Xкон |
16,04 |
63,26 |
81,41 |
|
6 Xнач |
16,04 |
63,26 |
81,41 |
|
Xсер |
17,51 |
69,04 |
88,69 |
|
Xкон |
18,98 |
74,83 |
95,97 |
|
7 Xнач |
18,98 |
74,83 |
95,97 |
|
Xсер |
20,45 |
80,61 |
103,25 |
|
Xкон |
21,92 |
86,39 |
110,53 |
7. Случайные величины распределяются по интервалам
Таблица 8
|
Интервал(1) |
1 |
Интервал(2) |
2 |
Интервал(3) |
3 |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
1,36 |
1 |
5,42 |
1 |
8,62 |
|
1,67 |
6,68 |
17,25 |
|||
|
2,13 |
8,51 |
19,54 |
|||
|
3,31 |
13,20 |
24,42 |
|||
|
3,44 |
13,73 |
||||
|
3,90 |
15,55 |
||||
|
2 |
4,75 |
2 |
18,95 |
2 |
26,39 |
|
4,87 |
19,43 |
29,50 |
|||
|
5,19 |
20,73 |
31,00 |
|||
|
5,26 |
21,00 |
31,79 |
|||
|
5,37 |
21,45 |
32,58 |
|||
|
5,88 |
23,47 |
34,03 |
|||
|
5,90 |
23,55 |
34,41 |
|||
|
6,18 |
24,66 |
34,92 |
|||
|
6,49 |
25,92 |
34,98 |
|||
|
6,86 |
27,38 |
37,57 |
|||
|
6,90 |
27,54 |
38,32 |
|||
|
6,97 |
27,83 |
39,26 |
|||
|
7,12 |
28,41 |
||||
|
3 |
7,34 |
3 |
29,30 |
3 |
40,65 |
|
7,35 |
29,34 |
41,94 |
|||
|
7,64 |
30,48 |
42,05 |
|||
|
7,68 |
30,65 |
42,59 |
|||
|
7,83 |
31,24 |
43,60 |
|||
|
8,03 |
32,05 |
43,68 |
|||
|
8,10 |
32,34 |
44,52 |
|||
|
8,30 |
33,12 |
44,77 |
|||
|
8,36 |
33,37 |
44,79 |
|||
|
8,38 |
33,45 |
44,84 |
|||
|
8,63 |
34,44 |
46,50 |
|||
|
8,69 |
34,68 |
47,23 |
|||
|
8,88 |
35,42 |
48,25 |
|||
|
8,93 |
35,62 |
48,60 |
|||
|
8,93 |
35,66 |
49,58 |
|||
|
9,25 |
36,91 |
49,59 |
|||
|
9,41 |
37,57 |
49,60 |
|||
|
9,50 |
37,91 |
50,32 |
|||
|
9,65 |
38,51 |
51,26 |
|||
|
9,69 |
38,66 |
52,67 |
|||
|
9,75 |
38,91 |
52,70 |
|||
|
9,88 |
39,45 |
52,76 |
|||
|
9,89 |
40,03 |
52,78 |
|||
|
4 |
10,03 |
4 |
4 |
||
|
10,47 |
41,77 |
52,76 |
|||
|
10,50 |
41,90 |
52,78 |
|||
|
10,50 |
41,92 |
54,13 |
|||
|
10,52 |
41,97 |
54,36 |
|||
|
10,58 |
42,23 |
55,53 |
|||
|
10,76 |
42,93 |
55,62 |
|||
|
10,79 |
43,06 |
56,22 |
|||
|
10,92 |
43,58 |
56,37 |
|||
|
11,07 |
44,18 |
56,47 |
|||
|
11,21 |
44,73 |
56,51 |
|||
|
11,26 |
44,92 |
56,87 |
|||
|
11,26 |
44,95 |
57,93 |
|||
|
11,55 |
46,08 |
58,86 |
|||
|
11,57 |
46,19 |
59,93 |
|||
|
11,73 |
46,82 |
60,47 |
|||
|
11,78 |
47,03 |
61,04 |
|||
|
11,88 |
47,42 |
61,19 |
|||
|
11,95 |
47,67 |
61,93 |
|||
|
12,20 |
48,68 |
61,99 |
|||
|
12,20 |
48,69 |
62,06 |
|||
|
12,36 |
49,31 |
62,61 |
|||
|
12,37 |
49,37 |
62,74 |
|||
|
12,48 |
49,81 |
65,83 |
|||
|
12,89 |
51,46 |
66,02 |
|||
|
66,03 |
|||||
|
66,19 |
|||||
|
5 |
13,12 |
5 |
52,37 |
5 |
66,89 |
|
13,16 |
52,53 |
67,08 |
|||
|
13,19 |
52,66 |
67,58 |
|||
|
13,33 |
53,21 |
68,04 |
|||
|
13,56 |
54,13 |
68,48 |
|||
|
13,65 |
54,48 |
68,52 |
|||
|
13,66 |
54,51 |
69,16 |
|||
|
13,79 |
55,02 |
69,17 |
|||
|
13,84 |
55,22 |
69,41 |
|||
|
13,95 |
55,66 |
69,97 |
|||
|
14,15 |
56,48 |
70,99 |
|||
|
14,51 |
57,92 |
72,65 |
|||
|
14,62 |
58,34 |
72,80 |
|||
|
14,67 |
58,53 |
73,34 |
|||
|
14,75 |
58,85 |
73,58 |
|||
|
14,80 |
59,06 |
73,97 |
|||
|
14,89 |
59,40 |
74,27 |
|||
|
15,03 |
59,98 |
74,67 |
|||
|
15,06 |
60,08 |
75,39 |
|||
|
15,49 |
61,80 |
75,53 |
|||
|
15,94 |
77,69 |
||||
|
79,07 |
|||||
|
79,98 |
|||||
|
Окончание таблицы 8 |
|||||
|
6 |
16,25 |
6 |
63,63 |
6 |
81,53 |
|
16,30 |
64,86 |
81,76 |
|||
|
16,79 |
65,04 |
82,23 |
|||
|
17,35 |
66,99 |
83,43 |
|||
|
17,39 |
69,24 |
83,45 |
|||
|
17,98 |
69,38 |
84,20 |
|||
|
18,22 |
71,76 |
87,22 |
|||
|
18,22 |
72,70 |
88,06 |
|||
|
72,72 |
92,67 |
||||
|
93,01 |
|||||
|
93,83 |
|||||
|
99,82 |
|||||
|
7 |
19,14 |
7 |
76,39 |
7 |
100,89 |
|
20,29 |
80,98 |
110,53 |
|||
|
21,65 |
81,92 |
||||
|
21,92 |
86,39 |
||||
8. Определяется количество попаданий случайных величин в интервалы.
Таблица 9
|
Номер интервала |
Выборка |
||
|
1 |
2 |
3 |
|
|
1 |
6 |
6 |
3 |
|
2 |
13 |
13 |
10 |
|
3 |
24 |
24 |
22 |
|
4 |
24 |
24 |
28 |
|
5 |
21 |
20 |
23 |
|
6 |
8 |
9 |
11 |
|
7 |
4 |
4 |
3 |
9. Рассчитываются относительные частоты попадания в интервалы: ni/N.
Таблица 10
|
Номер интервала |
Выборка |
||
|
1 |
2 |
3 |
|
|
1 |
0,06 |
0,6 |
0,03 |
|
2 |
0,13 |
0,13 |
0,1 |
|
3 |
0,24 |
0,24 |
0,22 |
|
4 |
0,24 |
0,24 |
0,28 |
|
5 |
0,21 |
0,2 |
0,23 |
|
6 |
0,08 |
0,09 |
0,11 |
|
7 |
0,04 |
0,04 |
0,03 |
10. Рассчитываются значения эмпирической функции распределения по интервалам:
fe = ni/(N dX).
Таблица 11
|
Номер интервала |
Выборка |
||
|
1 |
2 |
3 |
|
|
1 |
0,020429 |
0,005187 |
0,00206 |
|
2 |
0,044263 |
0,011238 |
0,00687 |
|
3 |
0,081716 |
0,020748 |
0,01511 |
|
4 |
0,081716 |
0,020748 |
0,01923 |
|
5 |
0,071502 |
0,01729 |
0,0158 |
|
6 |
0,027239 |
0,00778 |
0,00756 |
|
7 |
0,013619 |
0,003458 |
0,00206 |
11. Построение графика эмпирической функции распределения
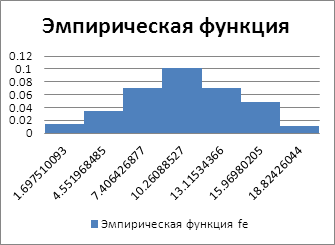
Рис.1. Распределение наработок на отказ автомобилей по 1 выборке
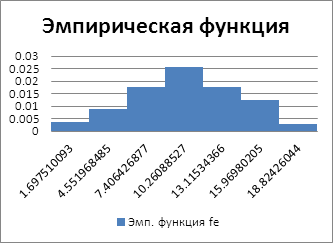
Рис.2. Распределение наработок на отказ автомобилей по 2 выборке
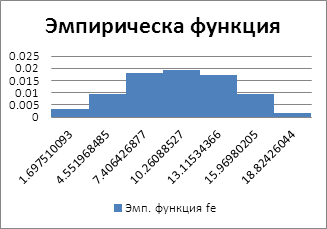
Рис.3. Распределение наработок на отказ автомобилей по 3 выборке
12. Рассчитывается среднее значение
Xcp = ( X1 + X2 + … XN)/N.
Таблица 12
|
Выборка |
|||
|
1 |
2 |
3 |
|
|
Xcp |
10,991 |
43,809 |
59,176 |
13. Математическое ожидание:
MX = ∑ Xсерini/N.
Таблица 13
|
Выборка |
|||
|
1 |
2 |
3 |
|
|
MX |
11,07994 |
43,82601 |
60,0118 |
14. Определение центрированных случайных величин по интервалам:
Xo = Xсер – MX.
Таблица 14
|
Номер интервала |
Выборка |
||
|
Хо |
1 |
2 |
3 |
|
1 |
-8,25 |
-32,62 |
-44,11 |
|
2 |
-5,32 |
-21,05 |
-29,55 |
|
3 |
-2,38 |
-9,49 |
-15,00 |
|
4 |
-0,56 |
2,08 |
-0,44 |
|
5 |
3,50 |
13,65 |
14,12 |
|
6 |
6,43 |
25,22 |
28,68 |
|
7 |
9,37 |
36,79 |
43,24 |
15. Центральный момент 2-го порядка:
M2 = ni/N ∑ ((Xсер – MX)2)
Таблица 15
|
Выборка |
|||
|
М2 |
1 |
2 |
3 |
|
24,52012 |
383,0807 |
175,132 |
|
16. Дисперсия:
Dx =M2.
Таблица 16
|
Выборка |
|||
|
Dx |
1 |
2 |
3 |
|
24,52012 |
383,0807 |
175,132 |
|
17. Среднее квадратическое отклонение:
Sx = Dx0.5
Таблица 17
|
Выборка |
|||
|
Sx |
1 |
2 |
3 |
|
4,951779 |
19,57245 |
13,2337 |
|
18. Коэффициент вариации:
Vx = Sx / M2.
Таблица 18
|
Выборка |
|||
|
Vx |
1 |
2 |
3 |
|
0,446914 |
0,446594 |
0,22052 |
|
19. Центральный момент 3-го порядка:
M3 = 1/N ∑ ((Xсер – MX) ·ni)3
Таблица 19
|
Выборка |
|||
|
M3 |
1 |
2 |
3 |
|
-1861,23 |
-117980 |
-359034 |
|
20. Центральный момент 4-го порядка:
M4 = 1/N ∑ ((Xсер – MX) ·ni)4.
Таблица 20
|
Выборка |
|||
|
M4 |
1 |
2 |
3 |
|
290188,3 |
55542703 |
1,11E+08 |
|
21. Асимметрия:
As = M3 / Sx3.
Таблица 21
|
Выборка |
|||
|
As |
1 |
2 |
3 |
|
-15,3291 |
-15,7353 |
-154,913 |
|
22. Эксцесс:
Ex = M4 / (Sx)4.
Таблица 22
|
Выборка |
|||
|
Ex |
1 |
2 |
3 |
|
482,6527 |
378,4832 |
3682,63 |
|
23. Расчеты представим в виде таблицы
Таблица 23
|
Интервал |
Начало интервала |
Конец интервала |
Середина интервала |
n |
n/N |
Xn/N |
(X-Xcp) |
|||
|
1 |
1,36 |
4,30 |
2,83 |
6 |
0,06 |
0,169 |
-8,25 |
|||
|
2 |
4,30 |
7,23 |
5,76 |
13 |
0,13 |
0,749 |
-5,32 |
|||
|
3 |
7,23 |
10,17 |
8,70 |
24 |
0,24 |
2,088 |
-2,38 |
|||
|
4 |
10,17 |
13,11 |
11,64 |
24 |
0,24 |
2,793 |
0,56 |
|||
|
5 |
13,11 |
16,04 |
14,57 |
21 |
0,21 |
3,061 |
3,50 |
|||
|
6 |
16,04 |
18,98 |
17,51 |
8 |
0,08 |
1,4 |
6,43 |
|||
|
7 |
18,98 |
21,92 |
20,45 |
4 |
0,04 |
0,818 |
9,37 |
|||
|
Xcp= |
10,991 |
Dx= |
24,52012 |
|||||||
|
Sx= |
4,95177 |
As= |
-15,3291 |
|||||||
|
Vx= |
0,4469 |
Ex= |
482,6527 |
|||||||
Таблица 24
|
Интервал |
Начало интервала |
Конец интервала |
Середина интервала |
n |
n/N |
Xn/N |
(X-Xcp) |
|
1 |
5,42 |
16,99 |
11,21 |
6 |
0,06 |
0,672 |
-32,62 |
|
2 |
16,99 |
28,56 |
22,77 |
13 |
0,13 |
2,960 |
-21,05 |
|
3 |
28,56 |
40,12 |
34,34 |
24 |
0,24 |
8,242 |
-9,49 |
|
4 |
40,12 |
51,69 |
45,91 |
24 |
0,24 |
11,02 |
2,08 |
|
5 |
51,69 |
63,26 |
57,48 |
20 |
0,2 |
11,496 |
13,65 |
|
6 |
63,26 |
74,83 |
69,04 |
9 |
0,09 |
6,214 |
25,22 |
|
7 |
74,83 |
86,39 |
80,61 |
4 |
0,04 |
3,224 |
36,79 |
|
Xcp= |
43,809 |
Dx= |
383,0807 |
||||
|
Sx= |
19,57245 |
As= |
-15,7353 |
||||
|
Vx= |
0,446594 |
Ex= |
378,4832 |
Таблица 25
|
Интервал |
Начало интервала |
Конец интервала |
Середина интервала |
n |
n/N |
Xn/N |
(X-Xcp) |
|
|
1 |
8,62 |
23,18 |
15,90 |
3 |
0,03 |
0,47697 |
-37,59 |
|
|
2 |
23,18 |
37,74 |
30,46 |
10 |
0,1 |
3,04578 |
-24,76 |
|
|
3 |
37,74 |
52,30 |
45,02 |
22 |
0,22 |
9,90361 |
-11,93 |
|
|
4 |
52,30 |
66,85 |
59,58 |
28 |
0,28 |
16,681 |
0,90 |
|
|
5 |
66,85 |
81,41 |
74,13 |
23 |
0,23 |
17,0507 |
13,73 |
|
|
6 |
81,41 |
95,97 |
88,69 |
11 |
0,11 |
9,75613 |
26,55 |
|
|
7 |
95,97 |
110,53 |
103,25 |
3 |
0,03 |
3,09752 |
39,38 |
|
|
Xcp= |
59,176 |
Dx= |
175,132 |
Vx= |
0,22052 |
|||
|
Ex= |
1627,47 |
Sx= |
15,034 |
As= |
-60,792 |
|||
24. Расчет теоретической функции распределения по нормальному закону

Где L
= X, 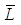 = Xcp,
= Xcp,  =Sx.
=Sx.
Для первой выборки:
Li
= Xi, 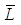 = Xcp = 10,500,
= Xcp = 10,500,
 =Sx=4,952
=Sx=4,952
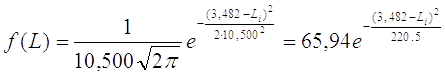

Рисунок 4. Построение графика для первой выборки
Для второй выборки:
Li
= Xi, 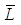 = Xcp = 43,809
= Xcp = 43,809 =Sx=19,57245.
=Sx=19,57245.

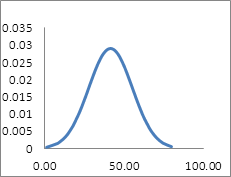
Рисунок 5. Построение графика для второй выборки
Для третьей выборки:
Li
= Xi, 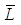 = Xcp = 59,176,
= Xcp = 59,176,  =Sx=13,23
=Sx=13,23
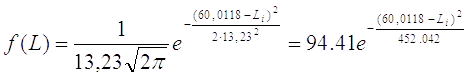
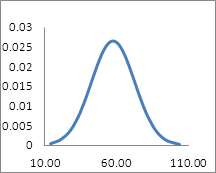
Рисунок 6. Построение графика для третьей выборки
25. Вероятность безотказной работы рассчитывается по уравнению
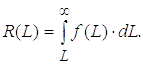
где dLi= Х(i+1) – Xi
Отказ
- событие, противоположное безотказной работе, поэтому вероятность отказа 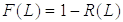
Для определения периодичности ТО, обеспечивающей заданную вероятность безотказной работы, строим график изменения R по наработке L.
Для первой выборки:

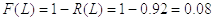
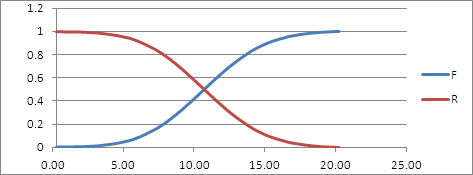
Рисунок 7. Определение периодичности ТО для первой выборки
Для второй выборки:
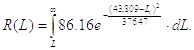

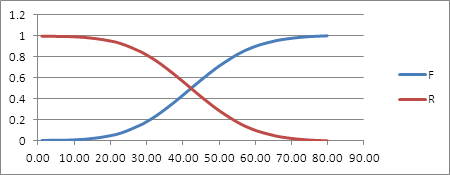
Рисунок 8. Определение периодичности ТО для второй выборки
Для третьей выборки:
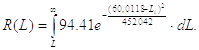
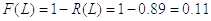
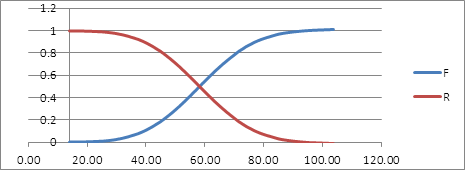
Рисунок 9. Определение периодичности ТО для третьей выборки
26. Определение периодичности ТО, обеспечивающей заданный уровень безотказности
|
1 выборка |
2 выборка |
3выборка |
|
|
Заданная вероятность безотказной работы |
0,94 |
0,88 |
0,89 |
|
Оптимальная периодичность ТО, тыс. км. |
3,9 |
23,55 |
43,86 |
27. Разработка режима ТО
|
Выборка |
3 |
9 |
15 |
21 |
27 |
33 |
39 |
42 |
|
1 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
2 |
- |
- |
- |
+ |
- |
- |
- |
- |
|
3 |
- |
- |
- |
- |
- |
- |
- |
+ |
ЗАКЛЮЧЕНИЕ
По результатам выполненной работы можно сделать вывод о необходимости следующей периодичности обслуживания автомобилей:
· для первой выборки – каждые 3,9 тыс.км.
· для второй выборки – каждые 23,55 тыс.км.
· для третьей выборки – каждые 43,86 тыс.км.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Аринин И.Н., Коновалов С.И., Баженов Ю.В. Техническая эксплуатация автомобилей. – М.: Транспорт, 2007.
2. Захаров Н.С., Сергиенко Е.В. Теория массового обслуживания / Учебное пособие. – Тюмень: ТюмГНГУ, 2011. – 90 с.
3. Захаров Н.С. Моделирование процессов изменения качества автомобилей. - Тюмень: ТюмГНГУ, 1999. – 127 с.
4. Положение о техническом обслуживании и ремонте подвижного состава автомобильного транспорта / Минавтотранс РСФСР. - М.: Транспорт, 1986. - 73 с.
5. Сарбиев В.И., Селиванов С.С., Коноплев В.Н., Демин Ю.Н. Техническое обслуживание и ремонт автомобилей. – М.: Недра, 2004.
6. Сервис транспортных и технологических машин и оборудования в нефтегазодобыче / Под ред. Н.С. Захарова. – Тюмень: ТюмГНГУ,2011.–499 с.
7. Шарыпов А.В., Осипов Г.В. Основы теории надежности и транспортных систем. – М.: Транспорт, 2008.













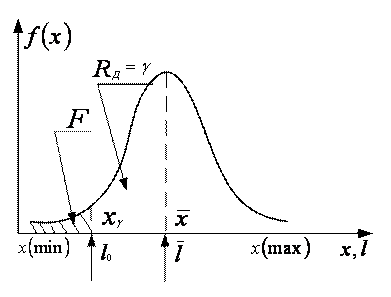
 (zip - application/zip)
(zip - application/zip)










