Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Санкт-Петербургский государственный лесотехнический университет имени С.М. Кирова
Кафедра технологии лесозаготовительных производств
КУРСОВОЙ ПРОЕКТ
на тему: «Планирование и организация эксперимента».
Выполнил:
Студент ЛИФ IV курс 3 группа
Бачериков И.В
№ зач.кн.: 108033
Проверил:
_________________________
дата _________________________
Санкт-Петербург
2012
1. СОДЕРЖАНИЕ
1. СОДЕРЖАНИЕ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
2. ВВЕДЕНИЕ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
3. ОПРЕДЕЛЕНИЕ ПРОЦЕНТА ГОДНОЙ ПРОДУКЦИИ И ТРЕБУЕМОЙ ТОЧНОСТИ НАСТРОЙКИ РАСКРЯЖЕВОЧНОЙ УСТАНОВКИ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
4. АНАЛИЗ СТАТИСТИЧЕСКИХ СВОЙСТВ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ ШЕРОХОВАТОСТИ ПОВЕРХНОСТИ ПИЛОМАТЕРИАЛОВ. . . . . . . . . . . . . . . . . . . . 8
5. ОПРЕДЕЛЕНИЕ ЗАВИСИМОСТИ ШЕРОХОВАТОСТИ ВЫПИЛИВАЕМЫХ ДОСОК ОТ ВРЕМЕНИ РАБОТЫ РАМНЫХ ПИЛ ПОСЛЕ ЗАТОЧКИ. . . . . . . . . . . . . . . . . . . . 12
6. ОБРАБОТКА РЕЗУЛЬТАТОВ ПОЛНОФАКТОРНОГО ПЛАНА И ПОСТРОЕНИЕ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ ПРОИЗВОДИТЕЛЬНОСТИ ТРЕЛЕВОЧНЫХ МАШИН. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7
7. ОПТИМАЛЬНЫЙ РАСКРОЙ ХЛЫСТА. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
8. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2. ВВЕДЕНИЕ
Высокие темпы развития теоретических наук на основе проработанного математического аппарата и необходимостью их экспериментального подтверждения требует из-за медленного развития технологий все более дорогостоящих экспериментов. При любом эксперименте невозможно избежать воздействия некоторых неучтенных помех, несмотря на стремление исследователя свести их к минимуму. Большинство из этих воздействий имеет случайную природу. Для возможности их частично компенсировать было разработано целое поднаправление математики — математическая статистика, которая позволяет оценивать параметры с частичным исключением помех.
3. ОПРЕДЕЛЕНИЕ ПРОЦЕНТА ГОДНОЙ ПРОДУКЦИИ И ТРЕБУЕМОЙ ТОЧНОСТИ НАСТРОЙКИ РАСКРЯЖЕВОЧНОЙ УСТАНОВКИ
Исходные данные:
n — количество наблюдений;
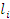 — наблюдаемые
длины сортиментов после раскряжевки, заданные в виде простого статистического
ряда.
— наблюдаемые
длины сортиментов после раскряжевки, заданные в виде простого статистического
ряда.
Исходные данные для определения процента годной продукции и требуемой точности настройки раскряжевочной установки.
Таблица 3.1
|
Номер наблюдения |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Длины сортиментов, см |
714 |
690 |
712 |
711 |
710 |
707 |
701 |
709 |
681 |
701 |
|
Номер наблюдения |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Длины сортиментов, см |
687 |
704 |
701 |
708 |
699 |
688 |
686 |
702 |
703 |
693 |
|
Номер наблюдения |
21 |
22 |
23 |
24 |
25 |
|
||||
|
Длины сортиментов, см |
675 |
709 |
704 |
688 |
707 |
|
||||
Заданные в виде простого статистического ряда длины сортиментов распологаем в виде неубывающей последовательности, т.е. строим вариационный ряд.
Таблица 3.2
|
Номер наблюдения |
|
|
|
Номер наблюдения |
|
|
|
|
1 |
675 |
-24,1 |
605,16 |
14 |
703 |
3,4 |
11,56 |
|
2 |
681 |
-18,6 |
345,96 |
15 |
704 |
4,4 |
19,36 |
|
3 |
686 |
-13,6 |
184,96 |
16 |
704 |
4,4 |
19,36 |
|
4 |
687 |
-12,6 |
158,76 |
17 |
707 |
7,4 |
54,76 |
|
5 |
688 |
-11,6 |
134,56 |
18 |
707 |
7,4 |
54,76 |
|
6 |
688 |
-11,6 |
134,56 |
19 |
708 |
8,4 |
70,56 |
|
7 |
690 |
-9,6 |
92,16 |
20 |
709 |
9,4 |
88,36 |
|
8 |
693 |
-6,6 |
4,56 |
21 |
709 |
9,4 |
88,36 |
|
9 |
699 |
-0,6 |
0,36 |
22 |
710 |
10,4 |
108,36 |
|
10 |
701 |
1,4 |
1,96 |
23 |
711 |
11,4 |
129,96 |
|
11 |
701 |
1,4 |
1,96 |
24 |
712 |
12,4 |
153,96 |
|
12 |
701 |
1,4 |
1,96 |
25 |
714 |
14,4 |
207,36 |
|
13 |
702 |
2,4 |
5,76 |
Итого |
17490 |
— |
2718 |
С помощью t-критерия Стьюдента исключаем из вариационного ряда анормальные результаты наблюдений. Для этого вычисляем:
Выборочное среднее: 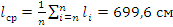 ;
;
Выборочную дисперсию: 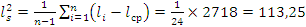 ;
;
Выборочное среднеквадратическое
отклонение: 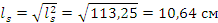 ;
;
Расчетный t-критерий:
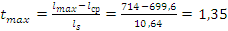 ;
;
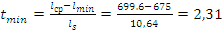 .
.
По числу степеней свободы 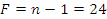 , принятому
уровню значимости
, принятому
уровню значимости 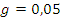 определяем t-критерий
Стьюдента. Если
определяем t-критерий
Стьюдента. Если 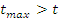 и
и 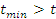 , то гипотеза
отвергается, значения
, то гипотеза
отвергается, значения 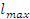 и
и 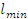 признаются
анормальными и исключаются из выборки. Проверку такого рода необходимо
производить до тех пор, пока не выполнится условие:
признаются
анормальными и исключаются из выборки. Проверку такого рода необходимо
производить до тех пор, пока не выполнится условие: 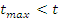 и
и 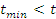 .
.
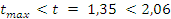 — условие
выполняется.
— условие
выполняется.
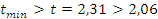 — условие не
выполняется.
— условие не
выполняется.
Располагаем результаты в виде вариационного ряда.
Таблица 3.3
|
Номер наблюдения |
|
|
|
Номер наблюдения |
|
|
|
|
1 |
681 |
-19,63 |
385,3369 |
14 |
704 |
3,37 |
11,3569 |
|
2 |
686 |
-14,63 |
214,0369 |
15 |
704 |
3,37 |
11,3569 |
|
3 |
687 |
-13,63 |
185,7769 |
16 |
707 |
6,37 |
40,5769 |
|
4 |
688 |
-12,63 |
159,5169 |
17 |
707 |
6,37 |
40,5769 |
|
5 |
688 |
-12,63 |
159,5169 |
18 |
708 |
7,37 |
54,3169 |
|
6 |
690 |
-10,63 |
112,9969 |
19 |
709 |
8,37 |
70,0569 |
|
7 |
693 |
-7,63 |
58,2169 |
20 |
709 |
8,37 |
70,0569 |
|
8 |
699 |
-1,63 |
2,6569 |
21 |
710 |
9,37 |
87,7969 |
|
9 |
701 |
0,37 |
0,1369 |
22 |
711 |
10,37 |
107,5369 |
|
10 |
701 |
0,37 |
0,1369 |
23 |
712 |
11,37 |
129,2769 |
|
11 |
701 |
0,37 |
0,1369 |
24 |
714 |
13,37 |
178,7569 |
|
12 |
702 |
1,37 |
1,8769 |
Итого |
16815 |
— |
2087,626 |
|
13 |
703 |
2,37 |
5,6169 |
С помощью t-критерия Стьюдента исключаем из вариационного ряда анормальные результаты наблюдений. Для этого вычисляем:
Выборочное среднее:
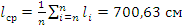 ;
;
Выборочную дисперсию:
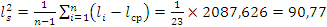 ;
;
Выборочное среднеквадратическое отклонение:
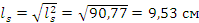 ;
;
Расчетный t-критерий:
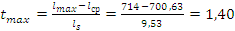 ;
;
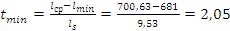 .
.
По числу степеней свободы 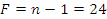 , принятому
уровню значимости
, принятому
уровню значимости 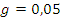 определяем t-критерий
Стьюдента. Если
определяем t-критерий
Стьюдента. Если 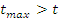 и
и 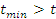 , то гипотеза
отвергается, значения
, то гипотеза
отвергается, значения 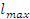 и
и 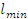 признаются
анормальными и исключаются из выборки. Проверку такого рода необходимо
производить до тех пор, пока не выполнится условие:
признаются
анормальными и исключаются из выборки. Проверку такого рода необходимо
производить до тех пор, пока не выполнится условие: 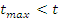 и
и 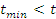 .
.
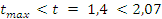 — условие
выполняется.
— условие
выполняется.
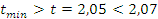 — условие
выполняется.
— условие
выполняется.
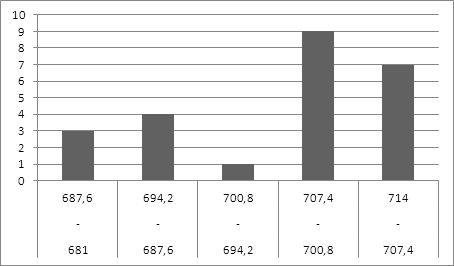
Для построения гистограммы, определяем числа разрядов (интервалов), для которых вычислим относительные или абсолютные частоты (количество попаданий той или иной случайной величины в интервал).
Определяем
число интервалов по формуле: 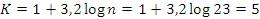
Шаг
интервала определяем по формуле: 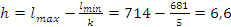
Полученные данные сводим в таблицу.
Данные для построения гистограммы и проверки степени согласования экспериментальных и теоретических законов.
Таблица 3.4
|
Номер интервала |
1 |
2 |
3 |
4 |
5 |
|
Границы интервала |
681 - 687,6 |
687,6 - 694,2 |
694,2 - 700,8 |
700,8 - 707,4 |
707,4 - 714 |
|
Середина интервала |
684,3 |
690,9 |
697,5 |
704,1 |
710,7 |
|
Экспериментальная частота, mc |
3 |
4 |
1 |
9 |
7 |
|
Теоретическая
частота, |
1,5709 |
3,8985 |
5,566 |
5,934 |
3,7076 |
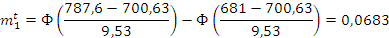
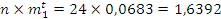
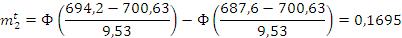
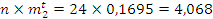
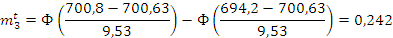
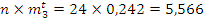
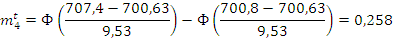
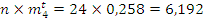
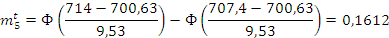
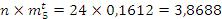
Проверяем согласование по критерию Пирсона:
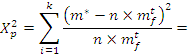
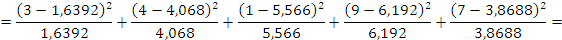
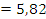
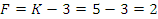
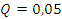
По числу степеней свободы и заданному уровню значимости определяем значение X2
По принятому закону распределения определяем вероятность попадания случайных величин в заданный интервал:
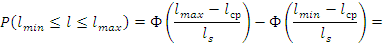
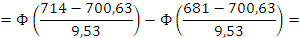
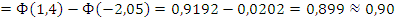
Выход готовой продукции 90%.
Вывод: на основе данного аналиа мы выяснили, что случайная величина подчиняется нормальному закону распределения, при хорошо налаженной установке выход годной продукции составит более 90%.
4. АНАЛИЗ СТАТИСТИЧЕСКИХ СВОЙСТВ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ ШЕРОХОВАТОСТИ ПОВЕРХНОСТИ ПИЛОМАТЕРИАЛОВ
Исходные данные для определения процента годной продукции и требуемой точности настройки раскряжевочной установки.
Таблица 4.1
|
Выборка №1 |
Номер наблюдения |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Длины сортиментов, см |
700 |
800 |
670 |
860 |
1070 |
710 |
630 |
600 |
780 |
730 |
|
|
Выборка №2 |
Номер наблюдения |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Длины сортиментов, см |
454 |
680 |
910 |
630 |
1140 |
700 |
770 |
510 |
550 |
490 |
Заданные в виде простого статистического ряда длины сортиментов распологаем в виде неубывающей последовательности, т.е. строим вариационный ряд.
Таблица 4.2
|
Номер наблюдения |
|
|
|
Номер наблюдения |
|
|
|
|
1 |
600 |
-155 |
24025 |
1 |
454 |
-229,4 |
52624,36 |
|
2 |
630 |
-125 |
15625 |
2 |
490 |
-193,4 |
37403,56 |
|
3 |
670 |
-85 |
7225 |
3 |
510 |
-173,4 |
30067,56 |
|
4 |
700 |
-55 |
3025 |
4 |
550 |
-133,4 |
17795,56 |
|
5 |
710 |
-45 |
2025 |
5 |
630 |
-53,4 |
2851,56 |
|
6 |
730 |
-25 |
625 |
6 |
680 |
-3,4 |
11,56 |
|
7 |
780 |
25 |
625 |
7 |
700 |
17,6 |
309,76 |
|
8 |
800 |
45 |
2025 |
8 |
770 |
86,6 |
7499,56 |
|
9 |
860 |
105 |
11025 |
9 |
910 |
226,6 |
51347,56 |
|
10 |
1070 |
315 |
99225 |
10 |
1140 |
456,6 |
208483,6 |
|
Итого |
7550 |
— |
165450 |
Итого |
6834 |
— |
408095 |
С помощью t-критерия Стьюдента исключаем из вариационного ряда анормальные результаты наблюдений. Для этого вычисляем:
Выборочное среднее:
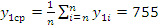 ;
;
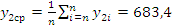 ;
;
Выборочную дисперсию:
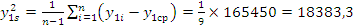 ;
;
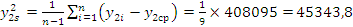 ;
;
Выборочное среднеквадратическое отклонение:
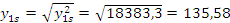 ;
;
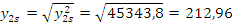 ;
;
Расчетный t-критерий:
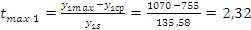 ;
;
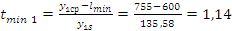 ;
;
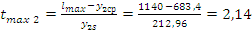 ;
;
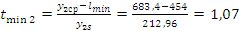 .
.
По числу степеней свободы 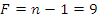 , принятому
уровню значимости
, принятому
уровню значимости 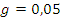 определяем t-критерий
Стьюдента.
определяем t-критерий
Стьюдента. 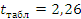
Если 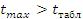 и
и 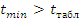 , то гипотеза
отвергается, значения
, то гипотеза
отвергается, значения 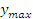 и
и 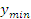 признаются
анормальными и исключаются из выборки. Проверку такого рода необходимо
производить до тех пор, пока не выполнится условие:
признаются
анормальными и исключаются из выборки. Проверку такого рода необходимо
производить до тех пор, пока не выполнится условие: 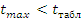 и
и 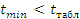 .
.
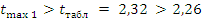 — условие не
выполняется.
— условие не
выполняется.
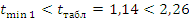 — условие
выполняется.
— условие
выполняется.
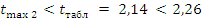 — условие
выполняется.
— условие
выполняется.
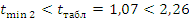 — условие
выполняется.
— условие
выполняется.
Продолжаем проверку выборки №1.
Таблица 4.3
|
Номер наблюдения |
|
|
|
|
1 |
600 |
-120 |
14400 |
|
2 |
630 |
-90 |
8100 |
|
3 |
670 |
-50 |
2500 |
|
4 |
700 |
-20 |
400 |
|
5 |
710 |
-10 |
100 |
|
6 |
730 |
-10 |
100 |
|
7 |
780 |
60 |
3600 |
|
8 |
800 |
80 |
6400 |
|
9 |
860 |
140 |
19600 |
|
Итого |
6480 |
— |
55200 |
Выборочное среднее:
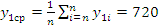 ;
;
Выборочную дисперсию:
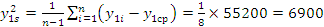 ;
;
Выборочное среднеквадратическое отклонение:
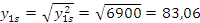 ;
;
Расчетный t-критерий:
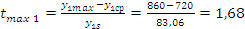 ;
;
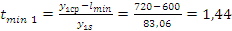 .
.
По числу степеней свободы 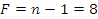 , принятому
уровню значимости
, принятому
уровню значимости 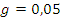 определяем t-критерий
Стьюдента.
определяем t-критерий
Стьюдента. 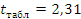
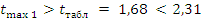 — условие
выполняется.
— условие
выполняется.
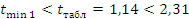 — условие
выполняется.
— условие
выполняется.
Проверяем однородность дисперсии по F-критерию Филера.
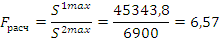
Задаем
уровень значимости: 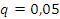
Число
степеней свободы: 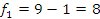 ;
; 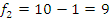
По
значениею f1 и f2 определяем
табличное значение критерия Фишера: 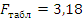
Получаем
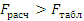 , значит
выборочные дисперсии считаются неоднородными для выбранного уровня значимости q.
, значит
выборочные дисперсии считаются неоднородными для выбранного уровня значимости q.
Проверяем однородность выборочных средних. S1 и S2 неоднородны, в данном случае формула tрасч имеет вид:
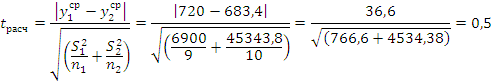
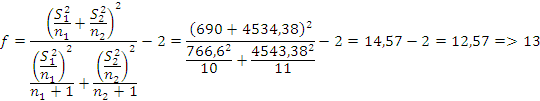
Найденое
значение f округляем до
целого и принимаем за число степеней свободы. По этой величине и по уровню
значимости 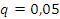 из таблиц
распределения Стьюдента отыскиваем tтабл:
из таблиц
распределения Стьюдента отыскиваем tтабл:
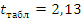
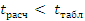
Проверяем оценку точности и надежности математического ожидания:
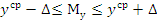
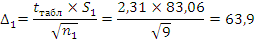
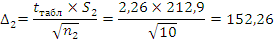
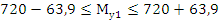
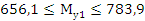
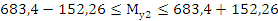
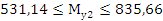
Определяе потребный объем случайной выборки:
Если
задаться допустимой производственнной точностью шероховатости поверхности
пиломатериалов ∆и доверительной вероятностью 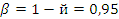 , то можно
определить потребный объем выборки.
, то можно
определить потребный объем выборки.
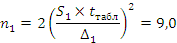
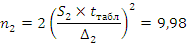
Вывод:
анализ статистических свойств измерений шероховатостей поверхности материалов
показал, что необходимое число замеров 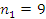 и
и 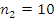
5. ОПРЕДЕЛЕНИЕ ЗАВИСИМОСТИ ШЕРОХОВАТОСТИ ВЫПИЛИВАЕМЫХ ДОСОК ОТ ВРЕМЕНИ РАБОТЫ РАМНЫХ ПИЛ ПОСЛЕ ЗАТОЧКИ
Исходные данные:
x — время работы рамных пил после заточки, ч
y — шероховатость поверхности досок, мм
Таблица 5.1
|
№ |
|
|
|
|
|
|
1 |
0,5 |
0,25 |
0,2 |
0,40 |
0,16 |
|
2 |
1,0 |
1,0 |
0,5 |
0,50 |
0,25 |
|
3 |
1,5 |
2,25 |
0,87 |
0,58 |
0,336 |
|
4 |
2,0 |
4 |
1,38 |
0,69 |
0,476 |
|
5 |
2,5 |
6,25 |
1,775 |
0,71 |
0,504 |
|
∑ |
7,5 |
13,75 |
4,725 |
2,88 |
1,726 |
Определяем коэффициент корреляции r между временем работы пил после заточки и шерохроватости поверхности выпиливаемых досок h.
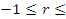
Коэффициент корреляции r вычисляем по формуле:
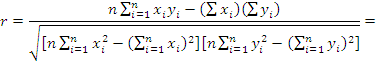
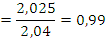
Оценка значимости коэффициента корреляции производится с помощью t-критерия. Для этого определяется:
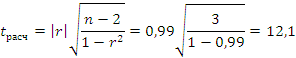
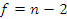 ,
, 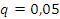 , следовательно,
, следовательно,
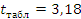
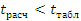 , значит
принимает гипотезу о некоррелированности величин x и y. В противном
случае r значимо
отличается от 0, т.е. между величинами x и y существует
линейная статическая связь.
, значит
принимает гипотезу о некоррелированности величин x и y. В противном
случае r значимо
отличается от 0, т.е. между величинами x и y существует
линейная статическая связь.
Оцениваем коэффициенты регрессии линейной и квадратичной моделей. Регрессионная модель в виде линейного уравнения имеет вид:
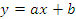
Коэффициенты регрессии определяем, решив систему уравнений:
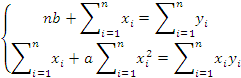
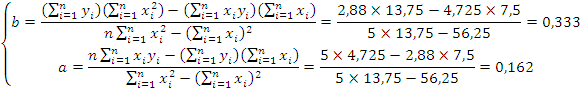
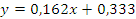
Строим график:
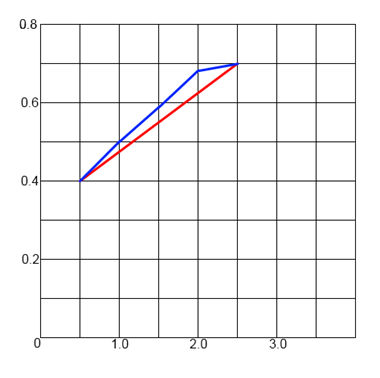
Рис. 5.1
Регрессионная
модель в виде квадратичного уравнения имеет вид: 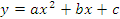
Для нахождения трех неизвестных коэффициентов регрессии, решим систему из трех линейных уравнений с тремя неизвестными:
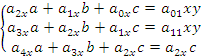
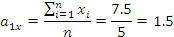
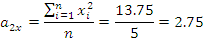
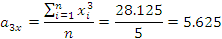
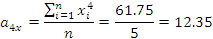
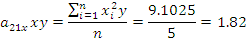
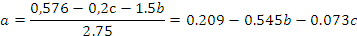
Подставляем все значения в последнее уравнение:
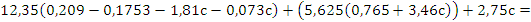
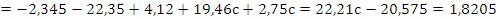
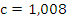
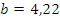
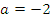
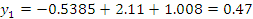
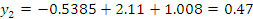
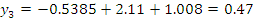
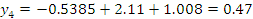
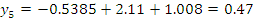
Строим график зависимости:

Рис. 5.2 График зависимости шероховатости досок от времени работы рамных пил
Вывод: в соответствии с проведенным анализом, мы выяснили, что зависимость шероховатости выпиливаемых досок от времени работы рамных пил после заточки определяется по линейной зависимости.
6. ОБРАБОТКА РЕЗУЛЬТАТОВ ПОЛНОФАКТОРНОГО ПЛАНА И ПОСТРОЕНИЕ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ ПРОИЗВОДИТЕЛЬНОСТИ ТРЕЛЕВОЧНЫХ МАШИН
Исходные данные:
Lтр — среднее расстояние трелевки, м;
Vхл — средний объем хлыста, м3;
Пч — часова производительность, м3/ч
Таблица 6.1
|
Показатель |
Данные |
||
|
Управляемые факторы (X1, X2) |
Расстояние трелевки Lтр, (X1) |
X1min, м X1max, м |
150 450 |
|
Объем хлыста Vхл, (X2) |
X2min, м3 X2max, м3 |
0,10 0,60 |
|
|
Выходная величина (отклик), Y |
Производительность трелевочного трактора, м3/ч |
1 |
11,0 11,2 11,0 10,5 10,8 |
|
2 |
5,8 6,2 6,0 6,1 5,9 |
||
|
3 |
16,1 15,9 16,4 16,8 16,7 |
||
|
4 |
9,1 9,8 9,2 8,9 8,8 |
||
Результаты расчета и эксперимента сводим в таблицу.
Таблица 6.2
|
Факторы |
Результаты эксперимента |
Результаты расчета |
|||||||||
|
Натуральные |
Нормализованные |
y1 |
y2 |
y3 |
y4 |
y5 |
|
|
|
||
|
Lтр,м |
Vхл,м3 |
X1 |
X2 |
||||||||
|
150 |
0,1 |
-1 |
-1 |
11.0 |
11.2 |
11.0 |
10.5 |
10.8 |
10.9 |
0.07 |
|
|
450 |
0,6 |
+1 |
-1 |
5.8 |
6.2 |
6.0 |
6.1 |
5.9 |
6.0 |
0.025 |
|
|
150 |
0,1 |
-1 |
+1 |
16.1 |
15.9 |
16.4 |
16.4 |
16.7 |
16.38 |
0.147 |
|
|
450 |
0,6 |
+1 |
+1 |
9.1 |
9.8 |
9.2 |
8.9 |
8.8 |
9.16 |
0.153 |
|
Определим уровни и интервалы варьирования факторов:
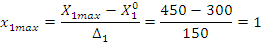
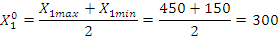
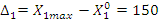
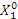 — основной
уровень варьирования фактора;
— основной
уровень варьирования фактора;
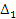 — интервал
варьирования фактора.
— интервал
варьирования фактора.
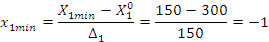
Аналогично находим верхний и нижний уровни варьирования среднего объема хлыста.
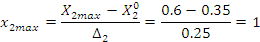
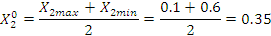
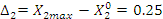

Рассчитываем средние и дисперсии для каждой серии опытов по формулам:
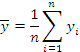
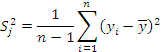
Отбрасываем аномальные результаты эксперимента и рассчитываем дисперсию воспромизводимости для каждой серии опытов.
Находим интервал мат. ожидания для каждой выборки:
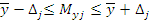
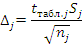
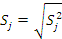
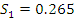
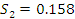
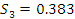
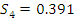
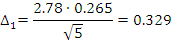
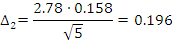
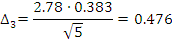
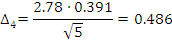
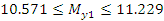
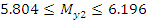
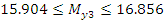
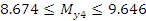
Результаты
эксперимента не входящие в полученные диапазоны из табл.6.2 удаляем и
пересчитываем значения 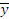 и
и 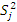 .
.
Таблица 6.3
|
Факторы |
Результаты эксперимента |
Результаты расчета |
|||||||||
|
Натуральные |
Нормализованные |
y1 |
y2 |
y3 |
y4 |
y5 |
|
|
|
||
|
Lтр,м |
Vхл,м3 |
X1 |
X2 |
||||||||
|
150 |
0,1 |
-1 |
-1 |
11.0 |
11.2 |
11.0 |
— |
10.8 |
11,0 |
0.02 |
|
|
450 |
0,6 |
+1 |
-1 |
— |
6.2 |
6.0 |
6.1 |
5.9 |
6.05 |
0.0125 |
|
|
150 |
0,1 |
-1 |
+1 |
16.1 |
— |
16.4 |
16.4 |
16.7 |
16.5 |
0.075 |
|
|
450 |
0,6 |
+1 |
+1 |
9.1 |
— |
9.2 |
8.9 |
8.8 |
9.0 |
0.025 |
|
Проверяем нормальность результатов:
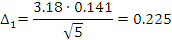
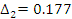
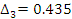
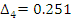
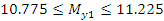
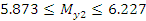
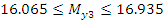

Для проверки однородности нескольких
дисперсий при равных объемах выборок 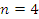 может быть
использован G-критерий
Кохрена. Пусть
может быть
использован G-критерий
Кохрена. Пусть 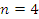 — количество
выборочных дисперсий, однородность которых проверяется. Обозначим эти дисперсии:
— количество
выборочных дисперсий, однородность которых проверяется. Обозначим эти дисперсии:
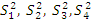 . Вычислим
расчетное G-отношение по
формуле:
. Вычислим
расчетное G-отношение по
формуле:
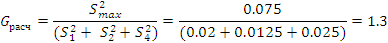
По выбранному уровню значимости q, числу степеней
свободы каждой выборки 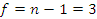 и по количеству
выборок N из таблицы
распределения Кохрена выбираем величину
и по количеству
выборок N из таблицы
распределения Кохрена выбираем величину 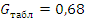 .
. 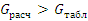 , следовательно
гипотеза о однородности дисперсий неверна.
, следовательно
гипотеза о однородности дисперсий неверна.
Вычисляем дисперсию воспроизводимости по формуле:

Число степеней свободы f для данной дисперсии равно:

Рассчитываем коэффициенты регрессионной
модели вида 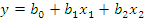 для нормальных
и натуральных факторов. Находим функции отклика.
для нормальных
и натуральных факторов. Находим функции отклика.
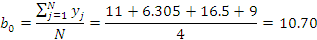
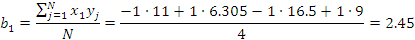
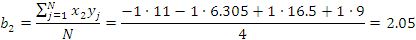
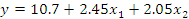
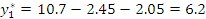
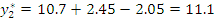
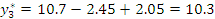
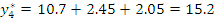
Регрессионная модель в натуральных обозначениях будет иметь вид:
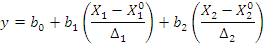
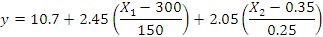
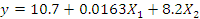
Запишем регрессионную модель в натуральных обозначениях:
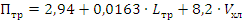
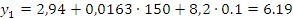
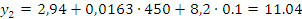
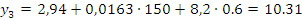
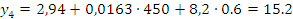
Оцениваем степень значимости коэффициентов регрессии:
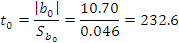
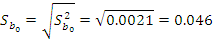
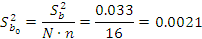
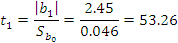
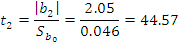
Вычисленную величину 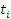 сравниваем с
табличным значением
сравниваем с
табличным значением 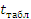 критерия
Стьюдента для заданного уровня значимости
критерия
Стьюдента для заданного уровня значимости 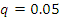 и числа
степеней свободы
и числа
степеней свободы 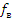 .
.
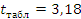
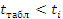
Проверка адекватности математической модели даст возможность ответить на вопрос, будет ли построенная модель предсказывать значения выходной величины с той же точностью, что и результаты эксперимента.
Определяем сумму квадратов, характеризующую адекватность модели:
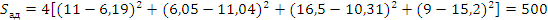
Вычисляем число степеней свободы дисперсии адекватности:
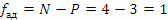
Вычисляем дисперсию адекватности:
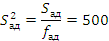
C помощью F-критерия Фишера
проверяем однородность дисперсии адекватности 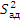 и дисперсии
воспроизводимости
и дисперсии
воспроизводимости 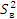 :
:
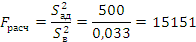
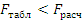
Модель неадекватна.
Строим
графики зависимости 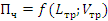
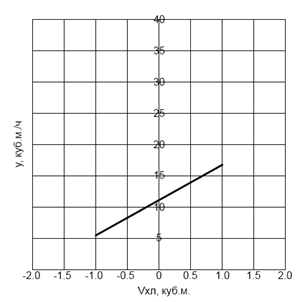
Рис. 6.1 График зависимости в нормальных обозначениях
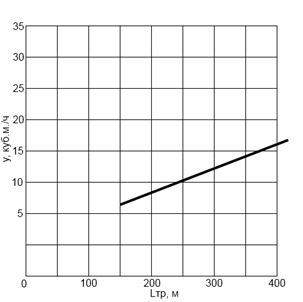
Рис. 6.2 График зависимости в натуральных обозначениях
7. ОПТИМАЛЬНЫЙ РАСКРОЙ ХЛЫСТА
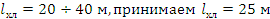
Кряжи 4, 5, 6 м.
1.
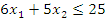
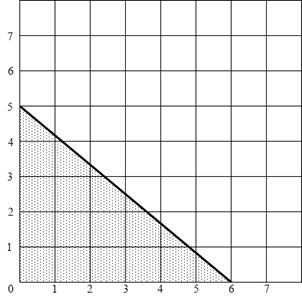 x
x
Рис. 7.1 Целочисленная решетка
2.
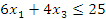
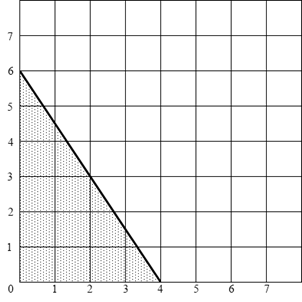
Рис. 7.2 Целочисленная решетка
3.
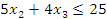
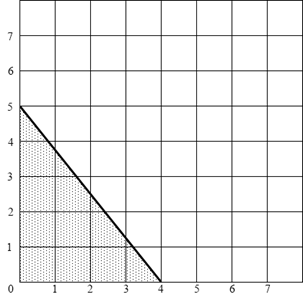
Рис. 7.3 Целочисленная решетка
8. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Андреев В.Н., Петровец В.Ф., Фаст В.И. Моделирование и оптимизация процессов лесозаготовок: Методические указания, рабочая программа и контрольные задания для студентов специальности 260100. ЛТА, 60 с. 1996г.














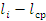

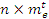
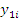
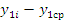
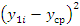
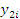
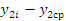
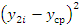

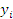
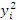
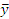
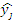
 (zip - application/zip)
(zip - application/zip)










