 Министерство
образования и науки Республики Казахстан
Министерство
образования и науки Республики Казахстан
Карагандинский государственный технический университет
Кафедра энергетики
Курсовая работа
по дисциплине «Теория электрических цепей 2»
Тема : Переходные процессы в линейных электрических цепях.
Проверил: Баландин В.С.
(оценка)
(подпись,
дата)
Сдал: гр. РЭТ-12-3
Игембаев А.
(подпись,
дата)
Караганда 2014
Дана электрическая цепь , в которой происходит коммутация. В цепи действует постоянная ЭДС Е. Определить закон распределения во времени распределения указанной в таблице величины.
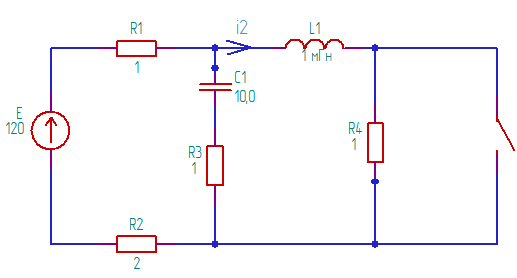
Рисунок 1 – Схема
Необходимо найти ток i2.
1) Записываем ток i2 в зависимости от времени:
i2= i2пр+ i2своб
2) Находим принудительную составляющую тока в момент времени t=∞
i2пр=E/(R1+R2)=40
3) Находим входное сопротивление, приравниваем к нулю, находим p:
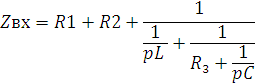
p1=-3348
p2=-22402
4) Записываем свободную составляющую:
i2своб=А1е-3348t+A2e-22402t
5) Записываем уравнения зависимости тока и производной от времени
i2(t)=40+ А1е-3348t+A2e-22402t
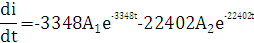
6) Записываем уравнения в момент времени t=0
i2(0)=40+ А1+A2
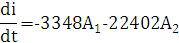
7) Находим iL(0) и uС(0)
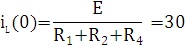
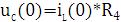
8) Составляем эквивалентную схему, по ней находим uL(0)
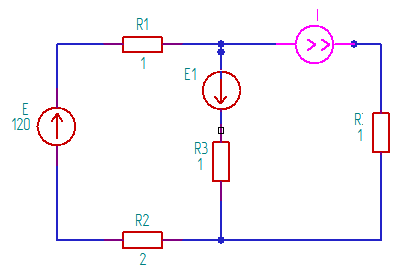
Рисунок 2 – Эквивалентная схема
E-E1=i1(0)(R1+R2)- i3(0)R3
i1(0)+ i3(0)= i2(0)
i3(0)R3+UL(0)+i2(0)*R4=E1
Согласно решению этого уравнения UL(0)=-15
UL(0)=L*(di/dt)
di/dt= -15*103
9) Находим A1 и A2
30=40 + А1+A2
-15*103=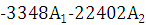
A1=-12,544
A2=2,544
Таким образом i2=40 -12,544е-3348t +2,544e-22402t
Для решения задачи операторным методом
1) Составляем операторную схему
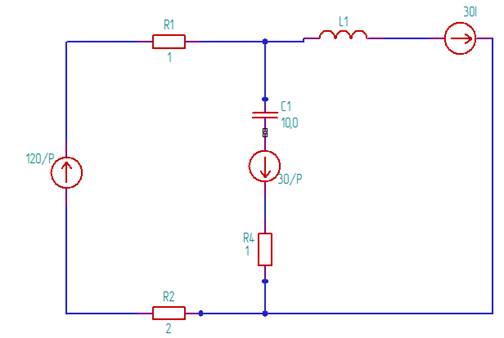
Рисунок 3 – Операторная схема
2) Составляем систему уравнений
I1(p)+I3(p)=I2(p)
I1(p)*3-I3(p)*(105/p+1)=150/p
I3(p)* (105/p+1)+I2(p)*p*10-3=30*10-3-30/p
3) Находим I2(p)
I2(p)=(30*p2+757500*p+3000000000)/(p3+25750*p2+75000000*p)
4) Преобразуем
Ak= (30*p2+757500*p+3000000000)/(3*p2+51500*p+75000000)
5) Подставляем и находим А1 и A2
A1=-12,544
A2=2,544
Таким образом i2=40 -12,544е-3348t +2,544e-22402t
Дана схема (рисунок 4) и график U1(t) (рисунок 5):
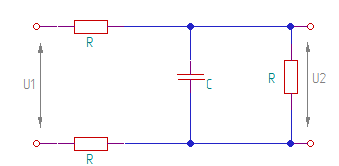
Рисунок 4 – Схема
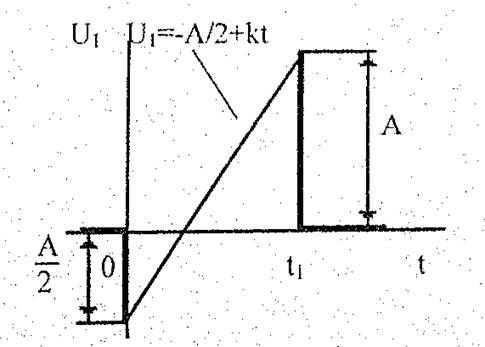
Рисунок 5 – График U1(t)
Необходимо найти U2 с помощью интеграла Дюамеля.
1) Находим k(t)
U2(t)= U2пр+ U2своб
U2пр=U1/3
Zвх=2R+1/(1/R+pC)=0
p= -3/(2CR)
U2(0)=0
U2(0)=U1/3+A
A=-U1/3
U2(t)= U1/3-(U1/3)*e-3t/(2CR)
k(t)=1/3 – 1/3* e-3t/(2CR)
2) Находим k(t-𝜏)
k(t-𝜏)= 1/3 – 1/3* e-3(t-𝜏)/(2CR)
3) Находим U1’(𝜏)
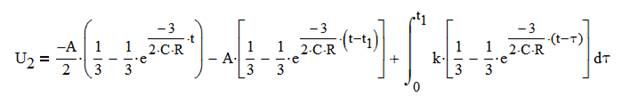 U1’(𝜏)=k
U1’(𝜏)=k
4) Подставляем в интеграл , интегрируем
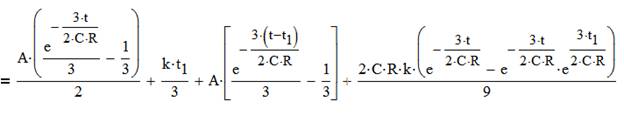
Упрощаем
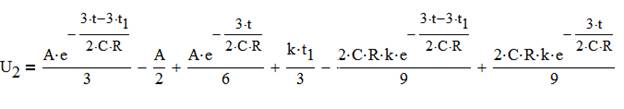













 (zip - application/zip)
(zip - application/zip)











