Особливі точки рівняння

Міністерство освіти і науки України

Дніпропетровський національний університет ім. Олеся Гончара

КОНТРОЛЬНА РОБОТА

з дисципліни „Диференціальні рівняння"

на тему „Особливі точки”

Виконавець: студентка групи

Назаренко Олеся

Перевірив:

м. Дніпропетровськ 2010 р.

Зміст

1. Особливі точки

2. Задача 1

3. Задача 2

4. Задача 3.

5. Задача 4

1. Особливі точки

Особливою точкою системи

 (1)

або рівняння

 (2)

де функції  й  неперервно диференційовані, називається така точка, в якій .

Для дослідження особливої точки системи

 (3)

або рівняння

 (4)

треба знайти розв^язок характеристичного рівняння

 (5)

Якщо розв^язки  дійсні, різні  й одного знаку , то особлива точка - вузол (рис.1, а), причому стійкий, якщо  й нестійкий, якщо .

Вузол характеризується тим, що всі траєкторії, крім однієї II, мають у точці (0,0) загальну дотичну I, що сама є траєкторією. Прямі I і II спрямовані вздовж власних векторів матриці , які відповідають  і , причому пряма I відповідає меншому за модулем з  і .

При  вузол є стійкою точкою спокою. На рис.1а стрілками показаний напрямок руху вздовж траєкторії при зростанні  у випадку стійкого вузла. Якщо , то вузол нестійкий і стрілки заміняються на протилежні.

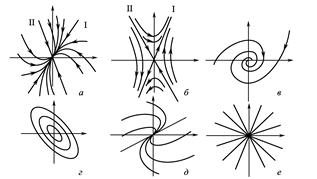
Рис.1. Типові траєкторії [2]

Якщо розв^язки  дійсні, різні  й різних знаків , то особлива точка - сідло (рис.1, б). Сідло є нестійкою точкою спокою.

Сідло характеризується наявністю двох траєкторій I і II, що проходять через (0,0) також у напрямку власних векторів. Пряма I є асимптотою для інших траєкторій при , а II є асимптотою при . Прямолінійна траєкторія I розташована за напрямком власного вектора, що відповідає додатньому , а прямолінійна траєкторія II за напрямком власного вектора, що відповідає від‘ємному . Прямі I і II називаються сепаратрисами сідла. На рис.1б стрілками показаний напрямок руху вздовж траєкторії при зростанні . Сепаратриса II є єдиною траєкторією, якій відповідає розв^язок, що прямує до 0 при . Тільки дві траєкторії I і II є прямолінійними. Інші траєкторії криволінійні й зі зростанням  йдуть із  в . Сепаратриси I і II розділяють фазову площину на 4 області, у яких лежать криволінійні траєкторії.

Якщо розв^язки  комплексні з дійсною частиною , відмінною від нуля, то особлива точка - фокус (рис.1, в), причому стійкий, якщо  й нестійкий, якщо . На рис.1в стрілками показаний напрямок руху при зростанні  у випадку стійкого фокуса.

Зауваження. У випадку фокуса траєкторії можуть бути закручені навколо (0,0) у різних напрямках. Для того, щоб визначити напрямок закручування, досить обчислити вектор швидкості  в якій-небудь точці, наприклад, в (0,1). Аналогічно досліджується напрямок руху у випадку центра й виродженого вузла.

Якщо розв^язки  комплексні чисто мнимі (), то особлива точка - центр (рис.1, г). Центр є стійкою, але не асимптотично стійкою точкою спокою.

Якщо розв^язки рівні й ненульові (тобто ), то особлива точка може бути виродженим вузлом (рис.1, д) або дикритичним вузлом (рис.1, е), причому дикритичний вузол має місце тільки у випадку системи  (або рівняння ), а у всіх інших випадках при  особлива точка є виродженим вузлом. У випадку виродженого вузла всі траєкторії дотикаються однієї прямої, спрямованої вздовж єдиного власного вектора, що відповідає . Дикритичний вузол може бути стійким  і нестійким .

Якщо ж один або обидва розв^язки рівняння (5) дорівнюють нулю, то , і, отже, дріб у правій частині рівняння (4) скорочується. Рівняння набуває вигляду , і розв^язок на площині XOY зображуються паралельними прямими.

 

2. Задача 1

 

Дослідити особливі точки рівняння. Накреслити інтегральні криві на площині XOY:

 

 

Розв^язання.

Для дослідження особливої точки рівняння

треба знайти розв^язок характеристичного рівняння

У нас , , , . Складаємо характеристичне рівняння

і розв^язуємо його відносно

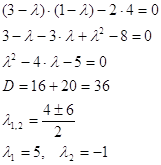
Розв^язки характеристичного рівняння дійсні й мають різні знаки.

Отже, особлива точка (0,0) - сідло. Сідло є нестійкою точкою спокою.

1. Перший спосіб побудови інтегральних кривих.

Власний вектор , що відповідає власному числу , знаходимо, підставляючи в рівняння

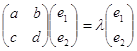
значення . Маємо

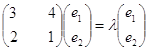
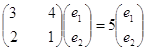
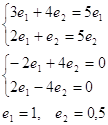
Власний вектор (1; 1/2) матриці коефіцієнтів даної системи, відповідає власному числу .

Далі, власний вектор , що відповідає власному числу , знаходимо, підставляючи в рівняння

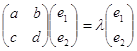
значення . Маємо

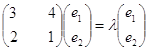
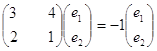
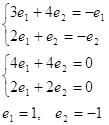
Власний вектор (1; - 1) матриці коефіцієнтів даної системи, відповідає власному числу .

На площині  будуємо прямі, спрямовані вздовж власних векторів (1; 1/2) і (1; - 1), а потім будуємо гіперболи.

2. Другий спосіб побудови інтегральних кривих.

Знайдемо сепаратриси сідла, тобто прямі, що розділяють гіперболи різних типів, які є фазовими кривими системи (тобто асимптоти цих гіпербол).

Прямі, що проходять через особливу точку (0,0), шукаємо у вигляді . Підставляючи  у вихідне рівняння

,

одержуємо рівняння для визначення коефіцієнта

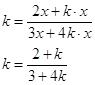
Таким чином, маємо дві шукані прямі

, .

3. Напрямок руху по траєкторіях. Для з"ясування напрямку руху по траєкторіях досить побудувати в якій-небудь точці  вектор швидкості . Наприклад, у точках  та вектор швидкості дорівнює

, ,

у точках  та вектор швидкості дорівнює

, ,

у точках  та  вектор швидкості дорівнює

, ,

у точках  та  вектор швидкості дорівнює

, .

Приблизний вид сім^ї інтегральних кривих зображено на рисунку 2.

Рис.2. Положення рівноваги й інтегральні криві [6]

 

3. Задача 2

 

Дослідити особливі точки рівняння. Накреслити інтегральні криві на площині XOY:

 

 

Розв^язання. Для дослідження особливої точки рівняння

треба знайти розв^язок характеристичного рівняння

У нас , , , . Складаємо характеристичне рівняння

і розв^язуємо його відносно

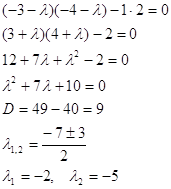
Розв^язки характеристичного рівняння дійсні, різні й одного знака.

Отже, особлива точка (0,0) - стійкий вузол ().

1. Перший спосіб побудови інтегральних кривих.

Власний вектор , що відповідає власному числу , знаходимо, підставляючи в рівняння

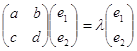
значення .

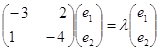
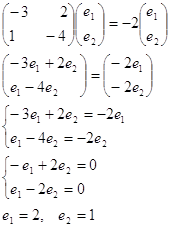
Власний вектор (2;

1) матриці коефіцієнтів даної системи, відповідає власному числу .

Далі, власний вектор , що відповідає власному числу , знаходимо, підставляючи в рівняння

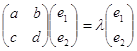
значення .

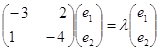
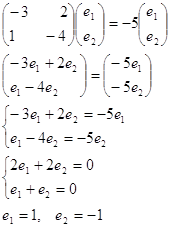
Власний вектор (1; - 1) матриці коефіцієнтів даної системи, відповідає власному числу .

На площині  будуємо прямі, спрямовані вздовж власних векторів (2;

1) і (1; - 1), а потім будуємо параболи й вказуємо напрямок руху по траєкторіях.

2. Другий спосіб побудови інтегральних кривих.

Прямі, що містять фазові криві системи, шукаємо у вигляді .

Підставляючи  у вихідне рівняння

,

одержуємо рівняння для визначення коефіцієнта :

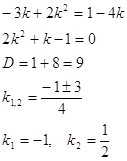
Виходить, що  і  - шукані прямі.

Фазові криві - частини парабол, що дотикаються на початку координат прямої . Параболи дотикаються саме прямої , оскільки власний вектор (2;

1) матриці коефіцієнтів даної системи, що відповідає власному числу , паралельний прямій .

3. Напрямок руху по траєкторіях.

Для з"ясування напрямку руху по траєкторіях досить побудувати в якій-небудь точці  вектор швидкості . Наприклад, у точці  вектор швидкості дорівнює

,

а в точці  вектор швидкості

.

Приблизний вигляд сім^ї фазових кривих зображений на рисунку 3.

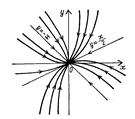
Рис.3. Положення рівноваги й інтегральні криві [6]

 

4. Задача 3.

 

Дослідити особливі точки системи. Накреслити інтегральні криві на площині XOY:

 

Розв^язання.

Для дослідження особливої точки системи

треба знайти розв^язок характеристичного рівняння

У нас , , , . Складаємо характеристичне рівняння

і розв^язуємо його відносно

Розв^язки характеристичного рівняння комплексні й різні.

Отже, особлива точка (0,0) - стійкий фокус ().

Напрямок руху по траєкторіях.

Для з"ясування напрямку закручування інтегральних кривих (спіралей) будуємо вектор швидкості  в точці (1,0):

Отже, спаданню  відповідає рух по спіралях за ходом годинникової стрілки. При русі за ходом годинникової стрілки інтегральні криві наближаються до початку координат (0,0).

Приблизний вигляд сім^ї інтегральних кривих зображено на рисунку 4.

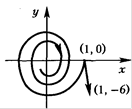
Рис.4. Положення рівноваги й інтегральні криві [6]

 

5. Задача 4

 

Дослідити особливі точки системи. Накреслити інтегральні криві на площині XOY:

Розв^язання.

Для дослідження особливої точки системи

треба знайти розв^язок характеристичного рівняння

У нас , , , . Складаємо характеристичне рівняння

і розв^язуємо його відносно

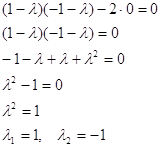
Розв^язки характеристичного рівняння дійсні й мають різні знаки. Отже, особлива точка (0, 0) - сідло. Сідло є нестійкою точкою спокою.

1. Перший спосіб побудови інтегральних кривих.

Власний вектор , що відповідає власному числу , знаходимо, підставляючи в рівняння

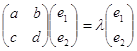
значення . Маємо

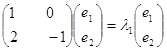
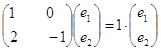
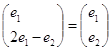
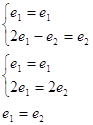
Власний вектор (1,1) матриці коефіцієнтів даної системи, відповідає власному числу .

Власний вектор , що відповідає власному числу , знаходимо, підставляючи в рівняння

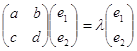
значення . Маємо

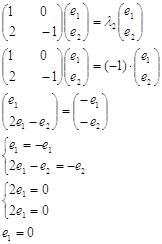
Власний вектор (0, ) матриці коефіцієнтів даної системи, відповідає власному числу .

На площині  будуємо прямі, спрямовані вздовж власних векторів (1;

1) і (0, ), а потім будуємо гіперболи.

2. Другий спосіб побудови інтегральних кривих.

Знайдемо сепаратриси сідла, тобто прямі, що розділяють гіперболи різних типів, які є фазовими кривими системи (тобто асимптоти цих гіпербол). Розділивши друге рівняння вихідної системи на перше рівняння, одержуємо

 або

Прямі, що проходять через особливу точку (0,0) шукаємо у вигляді  (а також ). Підставляючи  в останнє рівняння, одержуємо

Виходить, що  і  - шукані прямі.

3. Напрямок руху по траєкторіях.

Для з"ясування напрямку руху по траєкторіях досить побудувати в якій-небудь точці  вектор швидкості . Наприклад, у точці  вектор швидкості дорівнює

,

у точці  вектор швидкості

,

у точці  вектор швидкості

,

у точці  вектор швидкості

.

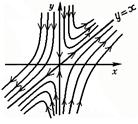
Рис.5. Положення рівноваги й інтегральні криві [6]

Список використаних джерел

1.         Боярчук А.К., Головач Г.П. Дифференциальные уравнения в примерах и задачах. Справочное пособие по высшей математике. - М.: Эдиториал УРСС, 2001. - 384 с.

2.         Васильева А.Б., Медведев Г.Н., Тихонов Н.А., Уразгильдина Т.А. Дифференциальные и интегральные уравнения, вариационное исчисление в примерах и задачах. - М.: ФИЗМАТЛИТ, 2003. - 432 с.

3.         Немыцкий В.В., Степанов В.В. Качественная теория дифференциальных уравнений. - М.: Государственное издание техникотеоретической литературы, 1947. - 448 с.

4.         Самойленко А.М., Кривошея С.А., Перестюк Н.А. Дифференциальные уравнения: примеры и задачи. Учеб. пособие. - 2е изд., перераб. - М.: Высш. шк., 1989. - 383 с.: ил.

5.         Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. - Ижевск, НИЦ "Регулярная и хаотическая динамика", 2000. - 176 с.