Основы технической эксплуатации защищенных телекоммуникационных систем

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(ФГБОУВПО «ВГТУ»)

Факультет информационных технологий и компьютерной безопасности Кафедра «Системы информационной безопасности»

Реферат

по дисциплине: «Основы технической эксплуатации защищенных телекоммуникационных систем»

на тему: «Вероятностные модели механизма старения информации. Ущерб от старения информации»

                                                    Выполнил:  студент группы БТ-081   

             Ушкин И. А. ________

   Руководитель:   д.т.н. , проф.

Остапенко А.Г._________

Воронеж 2013

Старение информации заключается в уменьшении ее ценности с течением времени. Старит информацию не само время, а появление новой информации, которая уточняет, дополняет или отвергает полностью или частично более раннюю.

Старение информации также влечет за собой снижение интереса к ней.Но ко многим стареющим информационным продуктам периодически возобновляется интерес со стороны тех или иных субъектов информационного производства. Это явление способствует обновлению забытого информационного продукта и позволяет сформулировать эмпирический закон старения информации, который гласит: «Интерес к информации обратно пропорционален времени, прошедшему с момента ее последнего проявления».

Вероятностные модели механизма старения информации

Интенсивность старения информации выражается в виде той части еще не учтенной полезной информации, которая может быть использована в прогнозной модели:

      или     

где

m(T), которая обозначает долю полезной информации в общем ее объеме;

п(Т) - глубина ретроспекции, выраженная в "квантах ин­формации" и использованная в модели, на момент времени Т;

N(Т) - нижняя граница сферы распространения полезной информации, выраженная в тех же единицах.

Под “квантом информации” будем понимать некоторый элемент, который может восприниматься и использоваться са­мостоятельно.

Глубина ретроспекции – период времени в прошлом, по которому имеется необходимая и достаточная информация об объекте.

Кумуляция информации – это ее систематизация, оценка и обобщение.

Интенсивность старения информации H(T) и h(T) определяет конкретную конфигурацию кривой h(T) или m(T).

Отсюда следует, что дифференциальное уравнение кумуляции информации имеет вид:

                                      

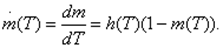
Интенсивность старения информации в общем случае будет зависеть от самых различных факторов. Поэтому функция h(t) можно записать в следующем общем виде

     h(T)=h(T,m(T),xi)

где xi – множество экзогенных факторов, определяющих конкретный процесс старения информации.

Здесь предполагается, что значения этих факторов явно не зависят от m(T), T. Дальнейший анализ динамики процесса старения информации состоит в спецификации вида функции h, который необходимо проводить исходя из эмпирических соображений.

Для выявления тенденций использования информации в исследованиях получило распространение аналитическое выравнивание эмпирических рядов распределения с помощью различных функций, которые описывают полиномы и комуляты распределения квантов информации, получаемые при наблюдении.

Существуют разные точки зрения относительно таких понятий, как ценность и старение информации. Так, например, старение информации определяется как закон изменения ценности информации во времени, рис. 1.

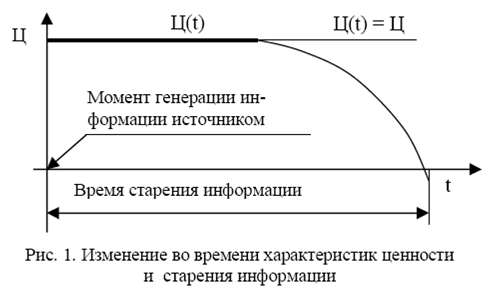
Взаимосвязь ценности и старения информации в данном случае определена. Однако она фактически исчезает, поскольку понятия ценности и старения информации не рассматриваются как самостоятельные и независимые друг от друга. Описанный выше подход к определению ценности и старения и их взаимосвязь (назовем его 1-м, типичным для большого количества работ) противоречит законам информации, сформулированным далее.

Другой подход основан на том, что не следует “совмещать” понятия ценности и старения информации, а рассматривать их как самостоятельные характеристики. Этот подход находится в соответствии с законами информации. Однако, он не устанавливает взаимосвязи ценности информации, определенной в связи с некоторой целью и ее старением, определенным как уровень ухода материального явления от своего первоначального базиса.

Рассмотрим принципиальные подходы при определении ценности информации. Ценность информации следует определять в связи с целью, для которой она используется, а также считать изменяющейся во времени при использовании с некоторой целью. В самом деле, если генерация информации произошла задолго до момента ее использования, то можно считать, что в момент времени tr ценность ее меньше максимальной. С другой стороны, когда обрабатывать и использовать ее уже поздно, ценность становится нулевой, т.е. обработкой и использованием информации потери на объекте уже предотвратить нельзя. Следовательно, между моментом генерации информации (сообщения) и моментом, когда она теряет свою ценность, должен существовать момент, когда она приобретает максимум ценности. Таким образом, возникает три вопроса:

1) Каков максимум в абсолютных или относительных единицах?

2) Где он расположен на оси времени?

3) Как изменяется ценность по обе стороны от него?

Значение максимума ценности информации можно определить через ущерб, который несет объект, если информация вообще не будет обработана и использована. Он может быть выражен как в абсолютных, так и в относительных единицах. При этом можно воспользоваться математическими моделями объектов и методами экспертных оценок. Сочетание обоих методов дает достаточно достоверные данные при правильно построенных шкалах и процедурах опроса. Для очень широкого класса объектов может быть найдена вероятность достижения цели в зависимости от какого-либо фактора (в частности, от времени использования информации). На рис. 2 представлен интегральный закон распределения F(t):

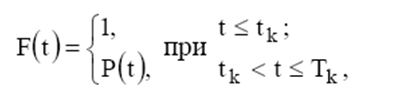
где

 F(t) – вероятность достижения цели в зависимости от момента использования информации;

t _k – момент максимума ценности сообщения;

T_k – момент времени, когда ценность сообщения становится равной нулю;

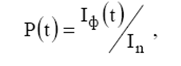
где I_ф(t) и I_п – фактические значения критерия эффективности системы при использовании информации в момент времени t и плановое, соответственно. Отметим, что эта формула справедлива лишь для случая максимизации критерия эффективности системы.

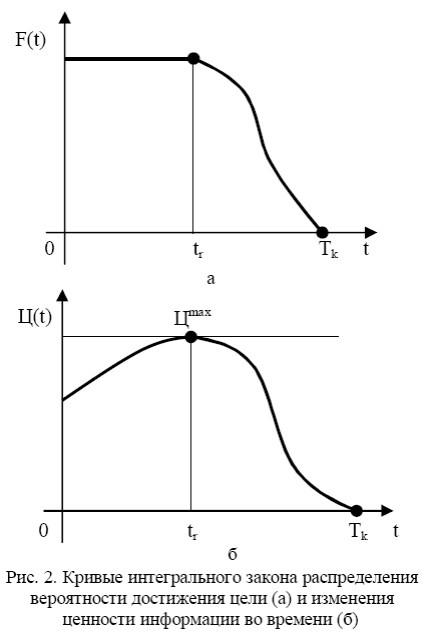
Однако, в случае его минимизации можно также получить аналогичную зависимость. В момент времени t=0 сообщение генерируется объектом. До момента t=t_k вероятность того, что сообщение будет обработано и использовано, и объект от его запаздывания не понесет потерь, близка к единице. С момента времени t=t_k вероятность достижения цели начинается падать и к моменту T_k практически равна нулю. Логично предположить, что в последний момент t=t_k , когда вероятность достижения цели еще остается близкой к единице, ценность сообщения приобретает максимум, а к моменту T_k она становится равной нулю. Естественно считать, что на интервале [t_k ,T] ценность сообщения падает по тому же закону, что и вероятность достижения цели объектом.

Таким образом, мы определили максимум ценности сообщения и закон ее убывания на интервале [t_k ,T_k] . Остается выяснять, как меняется Ц(t) на интервале [0, t_k] . Предположить строгую формализацию трудно, однако правдоподобным представляется соображение, что ценность сообщения должна расти от момента t=0 к моменту t=t_k . В первом приближении можно принять, что поскольку Ц(t) падает от максимума до нуля за время [t_k ,T_k] , то и на отрезке [0,T_k] она должна изменяться пропорционально отношению этих отрезков времени.

Изменение ценности информации во времени можно определить по формуле:

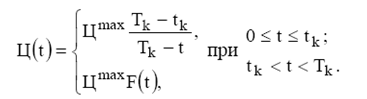
Формула дает лишь принцип определения ценности. Но совершенно очевидно, что реализуя оговоренные выше модели объектов, представляется возможным определить ценность различных классов информации. Подчеркнем, модели должны позволять определение Ц_max , t_k , T_k и F(t).

Рассмотрим вопросы взаимосвязи старения и ценности информации, представленные на рис. 3.

Взаимосвязь ценности и старения должна устанавливать требования к рациональной организации обработки и использования информации. Из рис. 3 видно, что точка 1 на временной оси является наиболее рациональной для реализации цели использования. Это точка с максимальной ценностью информации и к этому моменту должны быть выполнены все необходимые операции информационного процесса (передача, обработка и др.). Однако, пороговое время старения сообщения с моментом генерации t_r (T_порог.t_r)  соответствует точке 2. Если обработать и использовать информацию в рамках, не превышающих T_порог.t_r , то требование к системе обработки ужесточаются, что приведет к увеличению стоимости обработки, но может не привести к равнозначному эффекту от использования информации. Поэтому условия рациональной обработки информации с учетом ценности и старения можно сформулировать следующим образом:

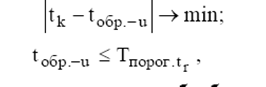
где t_обр._-u – момент окончания обработки и использования сообщения.

Условия (4) и (5) отражают взаимосвязь ценности и старения информации в процессе обработки и использования. Необходимо отметить, что наиболее удачным случаем с точки зрения рациональной организации обработки и использования информации является случай, когда t_k =T_порог._{t r} .

Поскольку момент t_k является моментом использования информации, то в некоторых случаях можно добиться совмещения элементов t_k и T_порог.t_r например, путем соответствующего выбора принятия решения по управлению объектом и др.

Список литературы.

1.     1. Ефимов А.Н. Информация, ценность, старение, рассеяние. – М.: Знание, 1978. – 64 с.

2.     Дворянкин С. В., Минаев В.А., Никитин М. М., Скрыль С. В., Фисун А. П. Правовое обеспечение информационной безопасности. 2008 г.

3.     Б.П Ивченко, Л.А. Мартыщенко, И.Б. Иванцов. «Информационная микроэкономика». Часть 1. Методы анализа и прогнозирования, СПб.: «Нордмед-Издат», 1997. – 160 с

4.     МОДЕЛЬ ВЗАИМОСВЯЗИ ЦЕННОСТИ И СТАРЕНИЯ ИНФОРМАЦИИ. Л.М. Виткин, В.У. Игнаткин. 2007 г.