Федеральное агентство связи
Московский технический университет связи и информатики
Кафедра технической электродинамики и антенн
«Курсовая работа по ЭМПИВ»
Тема1: Основные уравнения электродинамики
Проверил: доцент кафедры технической электродинамики и антенн Федотова Т.Н.
Выполнил: студент группы БЗС1101
Шишков Илья
Москва 2013
Задача № 1-21
В соответствии с заданием исследовать основные свойства монохроматического электромагнитного поля существующего в системе, изображенной на рисунке (прямоугольном волноводе).
Волновод заполнен однородной
изотропной средой с параметрами εr, μr, 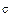 =0. Стенки волновода
являются идеально проводящими.
=0. Стенки волновода
являются идеально проводящими.
Известны выражения для составляющих векторов поля:
|
|
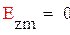
Исходные данные:
|
№ вар |
А/м |
|
|
a см |
b см |
ГГц |
ГГц |
|
|
2 |
6 |
1,5 |
1 |
50 |
30 |
2 |
7 |
1. Используя уравнения Максвелла, найти комплексные амплитуды всех остальных, и заданных в условии задачи, составляющих векторов E и H.
Для нахождения
комплексных амплитуд поперечных составляющих векторов Е и Н
используются соотношения и связывающие эти составляющие с комплексными
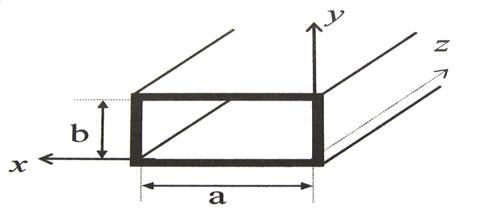
амплитудами продольных составляющих 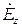 и
и
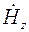 :
:
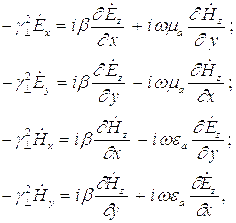
где
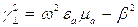
- поперечное волновое число, а b - коэффициент распространения волны вдоль направляющей системы.
Отсюда найдем все составляющие:
1) Exm:
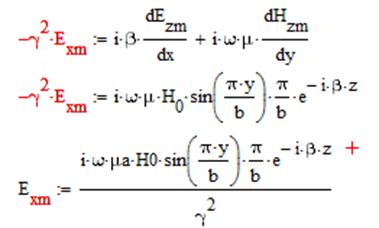
2) Eym:
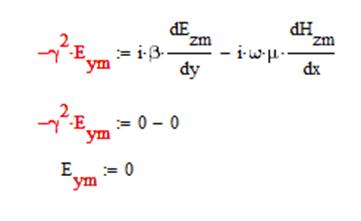
3) Hxm:
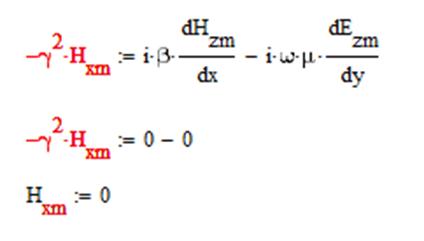
4) Hxm:
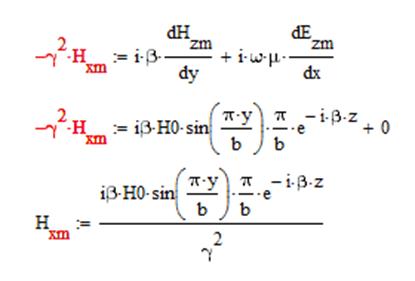
5)Hzm из условия:
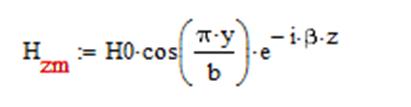
6)Ezm из условия:
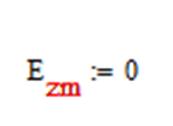
2.
Определим диапопзон частот в котором 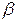 –
действительное число, т.е. рассматриваемое поле – бегущая волна.
–
действительное число, т.е. рассматриваемое поле – бегущая волна.
По
условию задачи 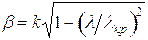 . Значит,
. Значит, 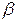 будет
действительным в случае, если
будет
действительным в случае, если
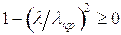 , т.е. при
, т.е. при 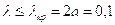 м.
м.
Этому диапозону длин волн соответствует диапозон частот:
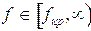 , где
, где 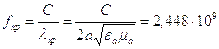 Гц
Гц
Если
частота волны не принадлежит рассчитанному диапозону частот, то 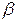 является мнимой
величиной. Для этого случая произведем замену:
является мнимой
величиной. Для этого случая произведем замену: 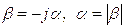 , для учета того
факта, при этом
, для учета того
факта, при этом 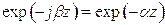 ,
, 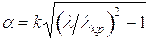
3.
Запишем выражения для мгновенных значений составляющих векторов поля 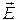 и
и 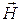 для двух случаев:
для двух случаев:
а)
когда 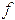 принадлежит
найденному в п. 2 диапозону частот,
принадлежит
найденному в п. 2 диапозону частот,
б)
когда 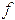 не принадлежит
этому диапозону.
не принадлежит
этому диапозону.
Для
получения выражений для мгновенных значений составляющих векторов поля
необходимо домножить их комплексные амплитуды на выражение 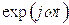 и, выделить
действительную часть.
и, выделить
действительную часть.
В первом случае выражения для комплексных амлитуд составляющих используются без изменений. Во втором случае необходимо произвести замену, описанную в пункте 2.
Тогда для случая а) получим выражения:
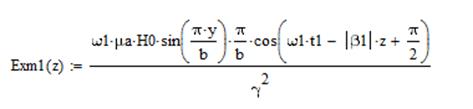
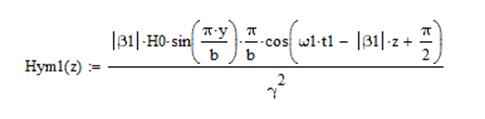
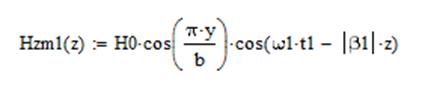
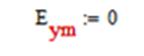
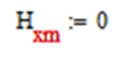
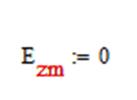
а для случая б) выражения будут иметь вид:
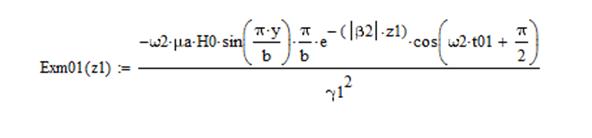
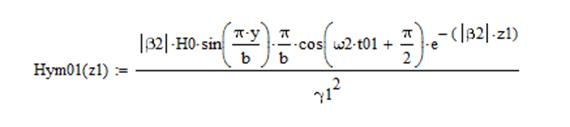
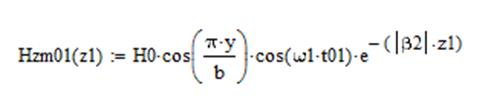
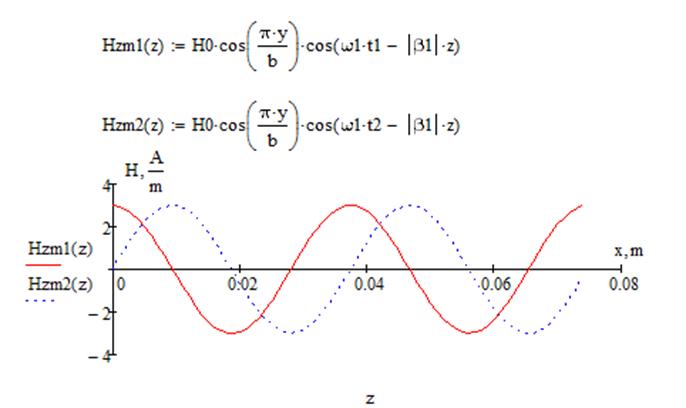
Построим графики амплитуд составляющих векторов полей от координаты z (при x=a/3, y=b/3) в 2 момента времени t1=0 и t2=T/4 в интервале от 0<=z<=2A, где A-длинна волны на частоте f2.


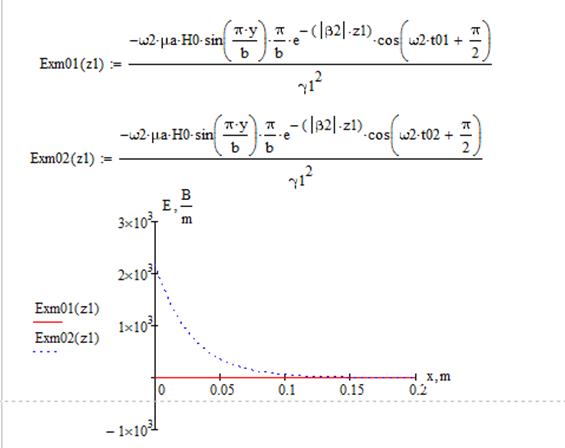
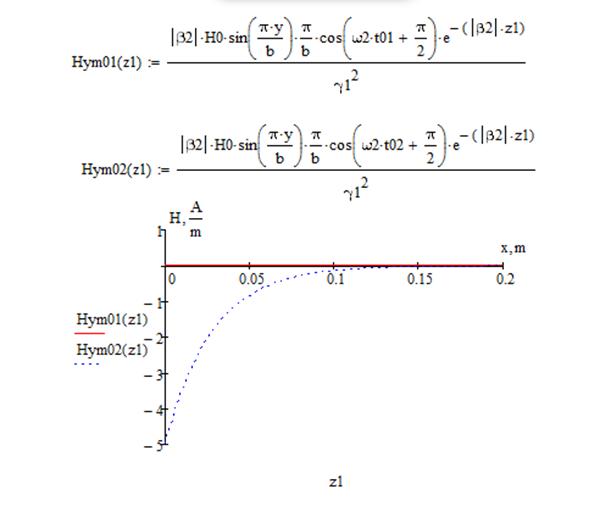
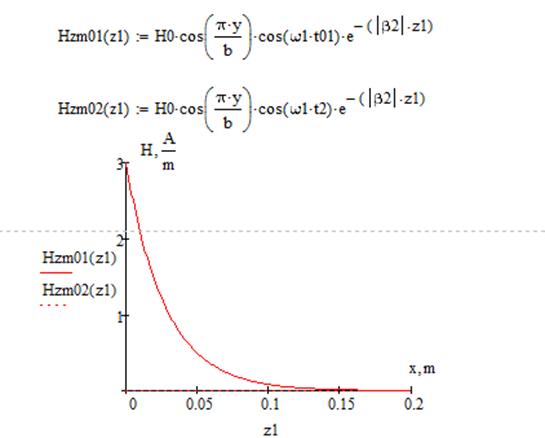
4. Проверить выполнение граничных условий (при х=0;а и у=0;в). Определить максимальные значения плотностей продольного и поперечного поверхностных токов на стенках волновода на частоте f2.
Проверка
граничных условий заключается в проверке истинности утверждений 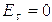 и
и 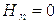 ,
т.е. равенста нулю касательной вектора
,
т.е. равенста нулю касательной вектора 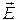 и нормальной вектора
и нормальной вектора 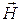 проекций (составляющих).
проекций (составляющих).
На боковой стенке (х=а) рассмотрению подлежат следующие составляющие:
Из полученного выше:
Ey=0
Hx=0
На нижней стенке волновода (y=0) рассмотрим:
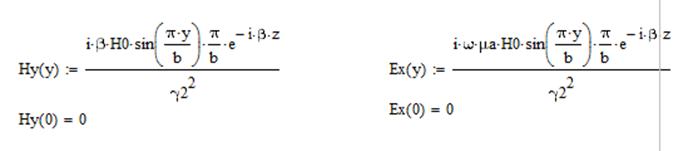
На верхней стенке волновода (y=b) рассмотрим:
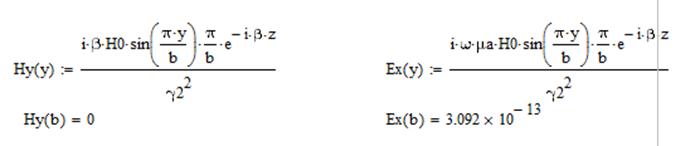
При обращении в ноль и граничные условия выполняются.
5. Вычислить средний за период поток энергии через поперечное сечение волновода на частоте f2.
Согласно граничным условиям на поверхности идеального металла плотность поверхностного тока определяется соотношением:
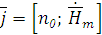 где n0–нормаль
к данной стенке волновода.
где n0–нормаль
к данной стенке волновода.
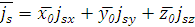
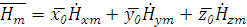
Найдем токи на нижней стенке волновода
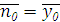

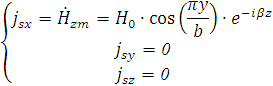
Максимальные значения плотностей
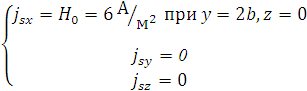
Найдем токи на верхней стенке волновода
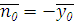
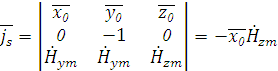
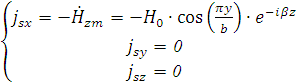
Максимальные значения плотностей
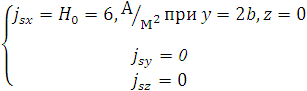
Найдем токи на правой стенке волновода
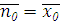
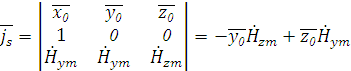
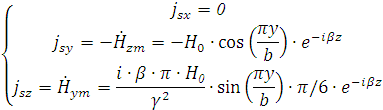
Максимальные значения плотностей
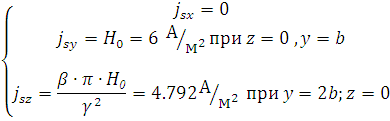
Найдем токи на левой стенке волновода
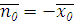
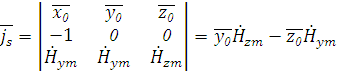
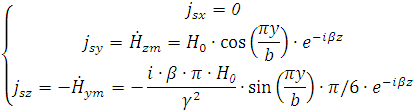
Максимальные значения плотностей
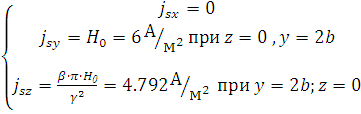
6. Вычислить средний за период поток энергии через поперечное сечение волновода на частоте f2.
Средний за период поток энергии, переносимый через поперечное сечение направляющей системы вычисляется по формуле
 ,
,
где 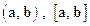 - скалярное и
векторное произведения векторов a и bсоответственно,
- скалярное и
векторное произведения векторов a и bсоответственно, 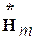 – функция
комплексно-сопряженная с
– функция
комплексно-сопряженная с 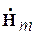 ,
а S^ – площадь
поперечного сечения волновода. Подставляя в формулу (1) S^ = dx dy, получаем
,
а S^ – площадь
поперечного сечения волновода. Подставляя в формулу (1) S^ = dx dy, получаем
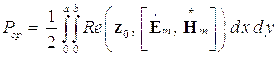 .
.
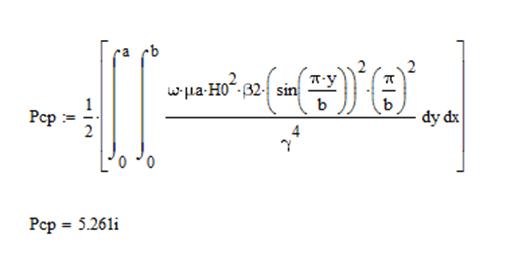
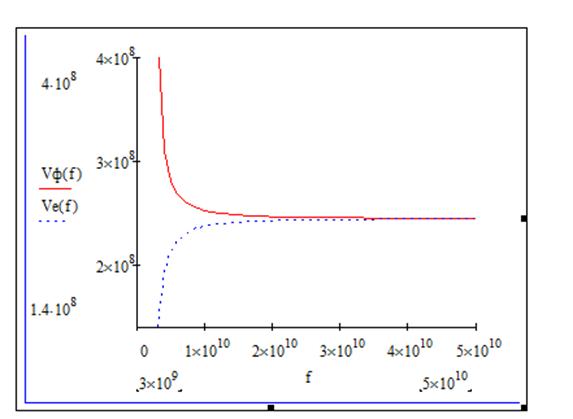
7. Определить фазовую скорость и скорость распространения энергии волны на частоте f2. Расчитать и построить графики зависимости этих скоростей от частоты.
Фазовая скорость и скорость распространения энергии определяются по формулам
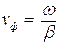 и
и
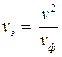 .
.

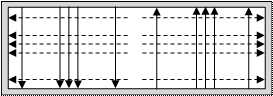
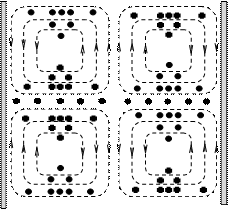
8. Нарисовать структуру векотрых линий полей и эпюры токов на стенках волновода.
Структуру векторных линий полей в волноводе следует строить в трех взаимно перпендикулярных сечениях прямоугольного волновода, причем в продольных сечениях (вдоль оси Z) должны размещаться две длины волны.
 |
 |
||||||
 |
|||||||
 |
|||||||














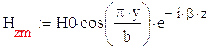
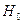
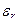
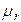
 (zip - application/zip)
(zip - application/zip)











