Оглавление
Введение. 1
Глава 1. Общие сведения об элементарных функциях. 3
1.1.Функция и ее свойства. 3
1.2. Элементарные функции. 4
Глава 2. Простейшие преобразования графиков. 13
2.1. Паралельный перенос. 13
2.2. Деформация (растяжение и сжатие графика) 15
2.3. Отражение. 16
2.4. Рекомендации по исследованию элементарных функций на уроках математики 18
Заключение. 22
Список использованной литературы.. 24
Введение
Трудно найти область науки или деятельности человека, где бы ни использовались графики. Всем нам приходилось видеть график роста ВВП страны, ВС страны, графики суточных или годовых изменений температуры, атмосферного давления и т. графики такого типа обычно строятся по данным составленных таблиц и используются для лучшего визуального анализа. На уроках математики мы обычно строим графики элементарных функций аналогичным методом, однако таблицы значений строятся в основном из приведенных формул, выражающих определенную зависимость, а не из полученных статистических данных. Потребность в подобных графиках, полученных из формул, возникает не только в математике. Так, например, анализируя теоретический ход будущего физического процесса, ученый получает формулу зависимости, позволяет находить зависимость одной величины относительно другой. Однако, только построив график по этой формуле, можно наглядно спрогнозировать будущий процесс, выраженный этой формуле, и внести соответствующие изменения в процесс для его улучшения. [4]
Однако построение графиков сложных функций по точкам, полученным из соответствующих формул, обычно не является рациональной, поскольку выбор точек не всегда может охватить все особенности графика. Поэтому меня заинтересовала построение графиков сложных функций с помощью анализа функции и использование элементарных графических преобразований графиков известных всем функций (параболы, гиперболы, линейной функции т.д.), с помощью которых можно построить намного сложнее и интереснее графики.
Стоит сказать также и об интересе самого процесса построения графиков, ведь построение графиков - одна из самых интересных тем в математике. Один из известных математиков нашего времени И. М. Гельфанд писал: «Процесс построения графиков является способом превращения формул и описан в геометрические образы. Это построение графиков - является средством увидеть формулы и функции и проследить, каким образом эти функции меняются. ... Такое умение видеть сразу и формулу, и ее геометрическую интерпретацию - является важным не только для изучения математики, но и для других предметов. Это умение, которое остается с Вами на всю жизнь, подобно умение ездить на велосипеде, печатать на машинке или водит машину ». Поэтому меня и заинтересовали графики, как предмет исследования, т. к. работа с ними приносит как практическую, так и эстетическую пользу инаслаждение.
Цель работы: проанализировать возможность графики элементарных функций и возможности их построения.
Актуальность работы: анализ функций и построение их графиков, необходимые для качественного исследования свойств и поведения зависимостей между величинами, т. к. график дает наглядную общую картину положения и развития исследуемого явления, позволяет визуально заметить те закономерности, содержит числовая информация.
При выполнении работы были поставлены следующие задачи: 1) построить графики функций элементарными методами; 2) научиться строить схематически графики функций, анализируя их свойства и поведение; 3) исследовать методы построения графиков; 4) расширить свои из практического использования в математике.
При
выполнении работы были достигнуты следующие результаты: 1) Выполняя построение различных графиков функций,
были рассмотрены общие принципы исследования функции и построения их графиков; 2) было рассмотрено комплексное
применение различных методов построения графиков функций; 3) Были рассмотрены сложные
функции и выполнены построения соответствующих графиков. 4) Выполняя работу, мною были
получены более глубокие
знания по анализу и графического построения функций. 5) Данная научная работа может быть использована
учащимися, для получения дополнительных знаний о построении графиков функций и учителями математики при проведении факультативных занятий.
Величина называется переменной (постоянной), если в условиях данной задачи она приобретает различные (только одного) значений.
Рассмотрим две переменные величины 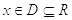 и
и 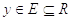 .
.
Определения. Функцией y = f (x) называется такое соответствие между множествами D и E, при которой каждому значению переменной х соответствует одно и только одно значение переменной у. При этом считают, что:
х - независимая переменная, или аргумент;
y - зависимая переменная, или функция;
f - символ закона соответствия;
D - область определения функции;
Е - множество значений функции.
Определение. Числовой функцией с областью определения х называется зависимость, при которой каждому числовому значению х из множества Х ставится в соответствие единственное некоторое число у. Обозначают функцию у = f (х). Переменную х называют независимой переменной или аргументом, переменную у - зависимой переменной или функцией.
Определения. Областью определения функции называется множество значений, которые приобретает независимая переменная х. Сказывается D (f).
Определения. Областью значений функции называется множество значений, которые приобретает зависимая переменная y при всех значениях х из области определения функции. Сказывается Е (f). Определения. Графиком функции у = f (x) называется множество точек М (х, f (x)) координатной плоскости, абсциссы которых принадлежат области определения функции, а ординаты являются соответствующими значениями этой функции. [6]
Пример: Найти область определения функций:
1) 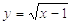
2) 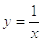 .
.
Решение.
1) Поскольку выражение, стоящее под знаком квадратного корня не может быть отрицательным, то чтобы найти область определения функции решим неравенство: х-1≥0 х≥1 Итак, D (f) = [1; + ∞].
2) Делит на ноль нельзя, поэтому область определения функции равна D (f) = (- ∞; 0) Ụ (0; + ∞).
Различают следующие способы задания функции: аналитический, графический, табличный, словесный.
1.2. Элементарные функцииОсновными элементарными функциями называют следующие функции.
1. Линейная функция y = ax + b, де a, b € R.(рис 1.1.)
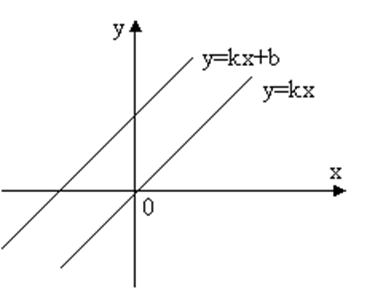
Рисунок 1.1 Линейная функция
2.
Степенная функции 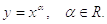
Область
определения функции и ее график зависят от значения α (рис. 1.2). Пусть,
α=n целое отрицательное число. Тогда 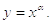
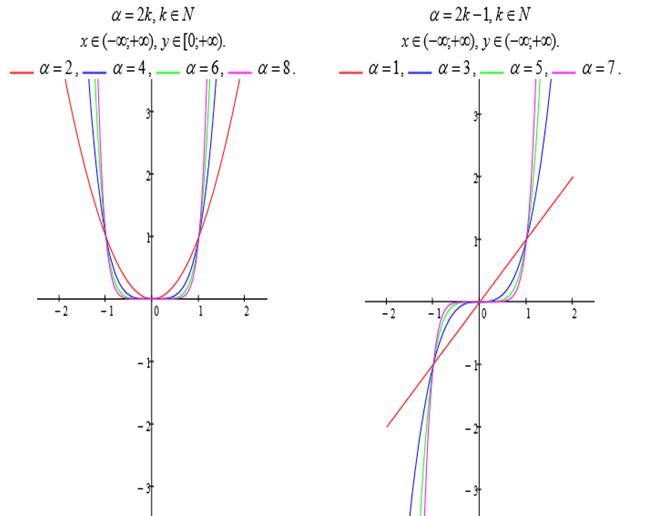
Рисунок 1.2. Степенная функция
Пусть, α=-n целое
отрицательное число. Тогда 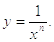 (рис.1.3)
(рис.1.3)
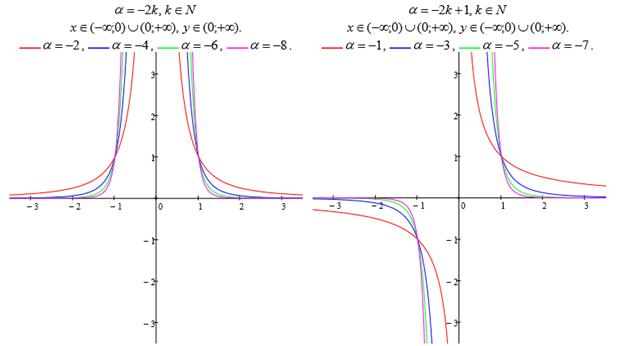
Рисунок 1.3. Степенная функция(α=-n целое отрицательное число)
Пусть, 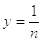 , где n -
натуральное число. Тогда
, где n -
натуральное число. Тогда 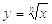 (рис.1.4)
(рис.1.4)
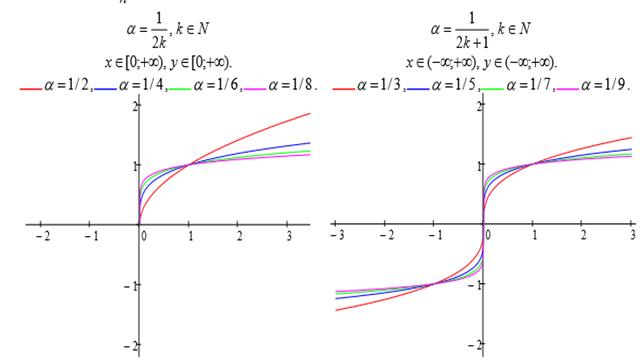
Рисунок 1.4. Степенная функция (n - натуральное число)
Пусть, 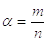 , где n и m –
взаимно простые натуральные числа. Тогда
, где n и m –
взаимно простые натуральные числа. Тогда 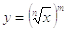 (рис.1.5, 1.6)
(рис.1.5, 1.6)
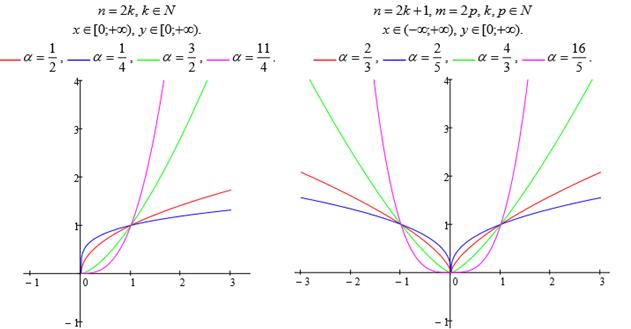
Рисунок 1.5. Степенная функция (n и m – взаимно простые натуральные числа)
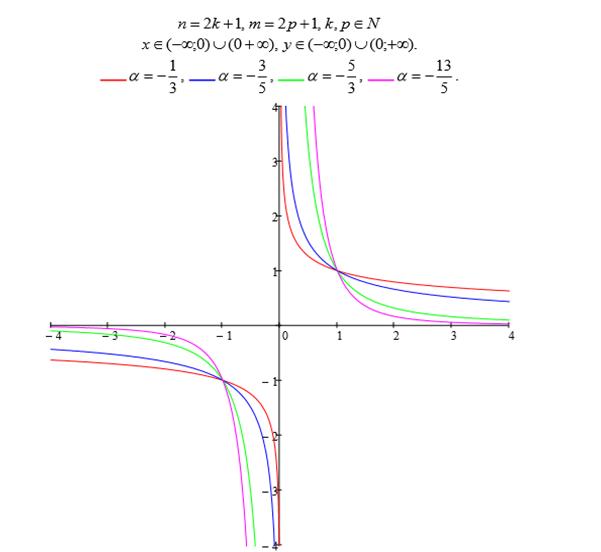
Рисунок 1.6. Степенная функция
В случае целых отрицательных показателей имеем.
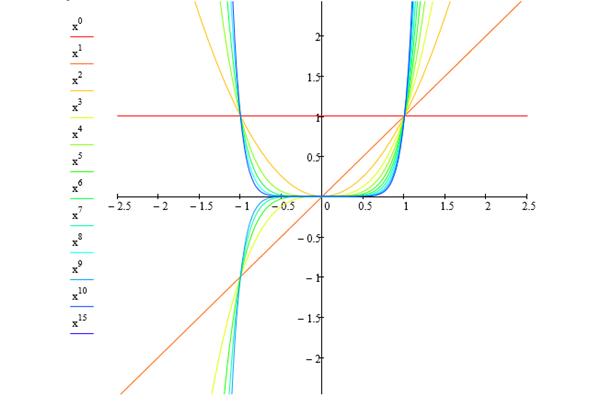
Рисунок 1.7. Степенная функция
В общем случае для положительных x имеем (рис.1.8).
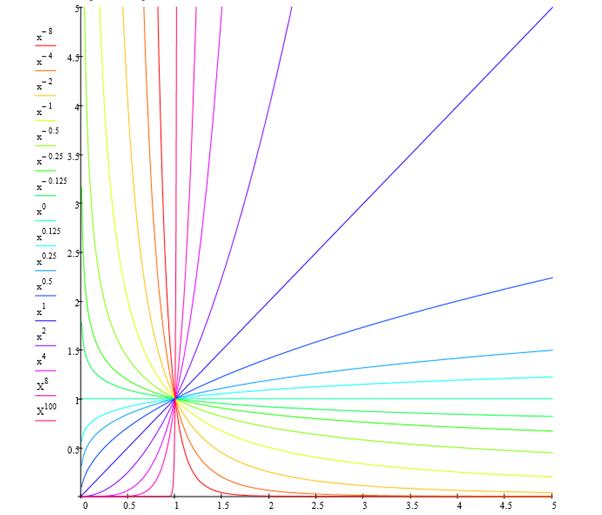
Рисунок 1.8. Степенная функция
3.
Показательная функции 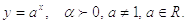
График показательной функции изображено на рисунке 1.9.
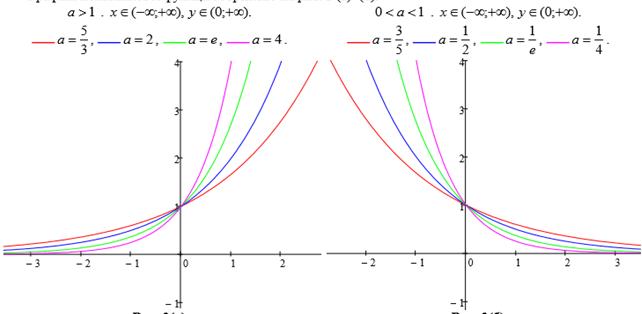
Рисунок 1.9. Показательная функция
4.
Логарифмическая функции 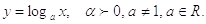
Графики логарифмической функции изображены на рисунке 1.10
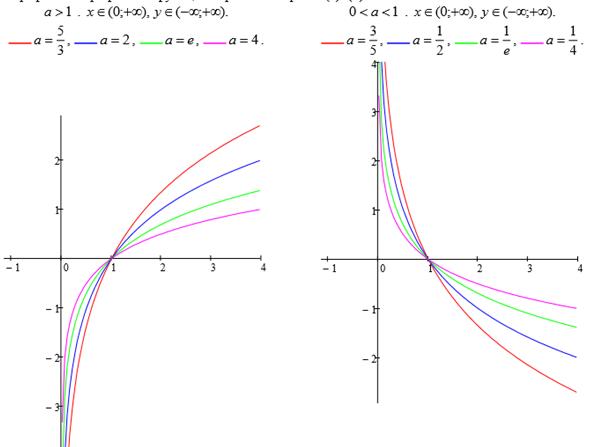
Рисунок 1.10. Логарифмическая функция
5. Тригонометрические функции у =cosx, y=sinx, y=tgx, y=ctgx
Графики тригонометрических функций изображено на графиках 1.11, 1.12, 1.13, 1.14
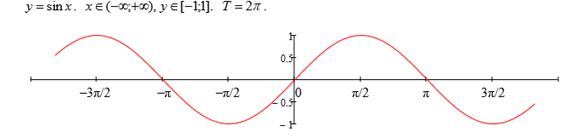
Рисунок 1.11. y=sinx
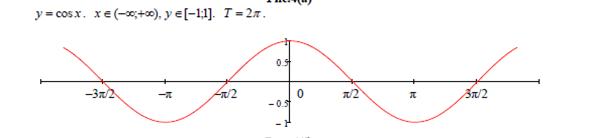
Рисунок 1.12. y=cosx
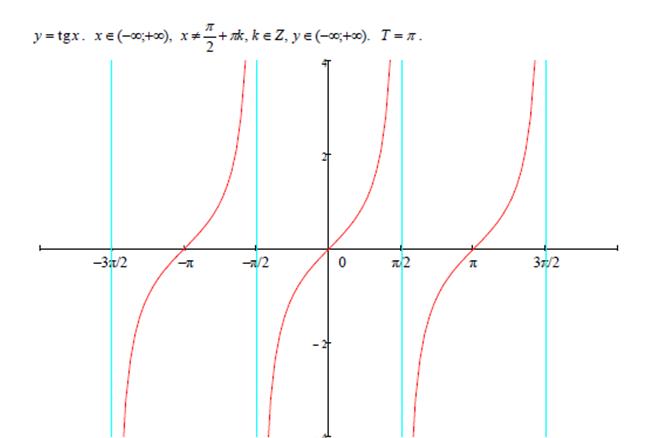
Рисунок 1.13. y=tgx
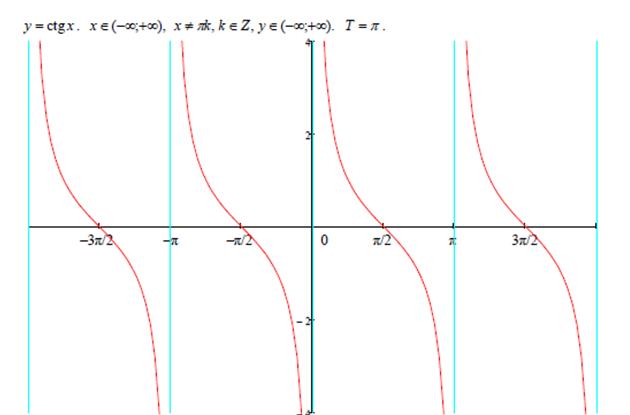
Рисунок 1.13. y=ctgx
Глава 2. Простейшие преобразования графиков 2.1. Паралельный перенос
Чтобы построить график функции, надо определить положениевсех его точек относительно некоторой системы координат Oxy. Однако в общем случае это сделать нельзя, поскольку подавляющее большинствографиков функций имеет бесконечное множество точек.
Обычно, строя «вручную» приближенно эскиз графика функции, определяют достаточно большое количество «близких» между собой точек графика.
Далее, на основании соответствующих свойств данной функции, эти точкипоследовательно соединяют одной или несколькими «плавными» линиями.
В элементарной математике много важных свойств функций не изучают. Средствами элементарной математики удается осуществлять построения графиков функций только в простейших случаях. [4]
Найти график функции  , выясним, как
выглядит график функции
, выясним, как
выглядит график функции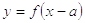 , гдеa=const.
, гдеa=const.
Если a >0, то
функция приобретает те х
же значений, что и функция 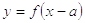 , но для значений x,
больших на a. Поэтому график
, но для значений x,
больших на a. Поэтому график 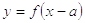 имеет
ту же форму, что и график
имеет
ту же форму, что и график  ,
однако он сдвинутый относительно
графика в положительном направлении оси Ox на a одиниц.
,
однако он сдвинутый относительно
графика в положительном направлении оси Ox на a одиниц.
3. Если a<0, то
график функции 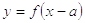 сдвинут
относительно графика
сдвинут
относительно графика  в
отрицательном направлении оси Ox на (-a) единиц.
в
отрицательном направлении оси Ox на (-a) единиц.
4. Итак, чтобы
построить график 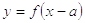 график
паралельно переносят вдоль оси Ox на a (влево для a < 0, вправо a>0)
(рис.2.1)
график
паралельно переносят вдоль оси Ox на a (влево для a < 0, вправо a>0)
(рис.2.1)
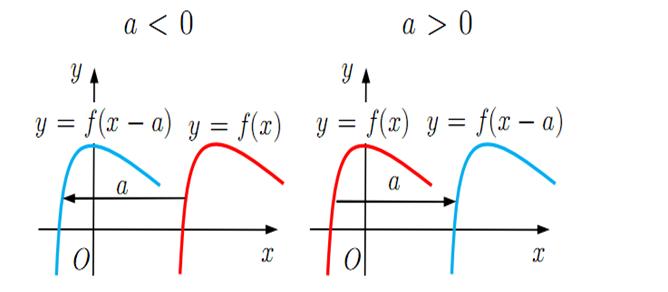
Рис. 2.1. Параллельный перенос графика вдоль оси Ox
Параллельный перенос графика вдоль оси ординат
При тех же значениях x
значение функции 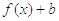 отличаются
от значений функции
отличаются
от значений функции  на число
b.
на число
b.
Если b>0, то
значение 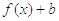 больше от
значений
больше от
значений  на b, а если
b<0, то – меньше значений
на b, а если
b<0, то – меньше значений  на(-b).
[1]
на(-b).
[1]
3. Итак, чтобы
построить играфик 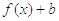 график
график  параллельно
переносят вдоль оси Oy на b (вниз для b<0, вверх для b>0).
параллельно
переносят вдоль оси Oy на b (вниз для b<0, вверх для b>0).
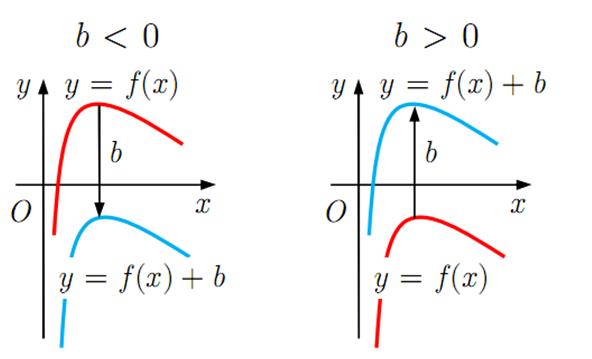
Рис. 2.2. Параллельный перенос графика вдоль оси Oy
2.2. Деформация (растяжение и сжатие графика)Сжатия (растяжения) вдоль оси абсцис
Считая, что график
функции  известен, выясним,
который выглядит график функции
известен, выясним,
который выглядит график функции 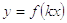 ,
где k =const>0.
,
где k =const>0.
Функция 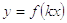 принимает тех же
значений, что и функция
принимает тех же
значений, что и функция  , но
для значений x, разделенных на k. К примеру, для
, но
для значений x, разделенных на k. К примеру, для 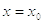 значение функции
f(x) равна
значение функции
f(x) равна 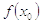 ; функция
; функция 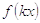 также принимает
значение
также принимает
значение 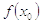 , но для
, но для 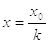 .
.
Поэтому, чтобы из
графика функции  получить
график функции
получить
график функции 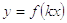 ,
достаточно абсциссы всех точек этого графика разделить на k (остаток неизменной
ординаты). [3]
,
достаточно абсциссы всех точек этого графика разделить на k (остаток неизменной
ординаты). [3]
Итак, чтобы построить
график 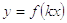 , график
, график  розтягивают в
розтягивают в 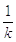 раз (0< k<1)
вдоль оси Ox или сжимают в k раз (k >1) вдоль оси Ox.
раз (0< k<1)
вдоль оси Ox или сжимают в k раз (k >1) вдоль оси Ox.
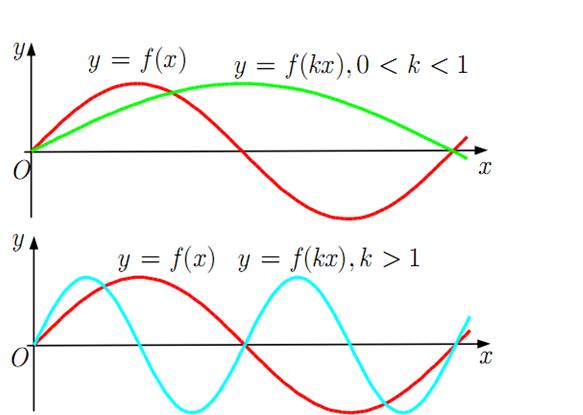
Рис. 2.3. Растяжение и сжатие графика функции вдоль оси ОY
Сжатия (растяжения) вдоль оси ординат
Пусть задано график
функции  . Выясним, как
выглядит график функции
. Выясним, как
выглядит график функции  ,
где c=const>0.
,
где c=const>0.
Для каждого допустимого
значения аргумента 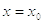 значение
функции
значение
функции  равен значению
функции
равен значению
функции  , умноженному на c.
, умноженному на c.
Поэтому, чтобы из
графика  достать график
достать график 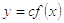 , достаточно
ординаты всех точек этого графика умножить на c (оставив неизменными абсциссы).
[7]
, достаточно
ординаты всех точек этого графика умножить на c (оставив неизменными абсциссы).
[7]
Итак, чтобы построить
график 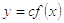 , график
, график  сжимают в
сжимают в  раз (0
раз (0
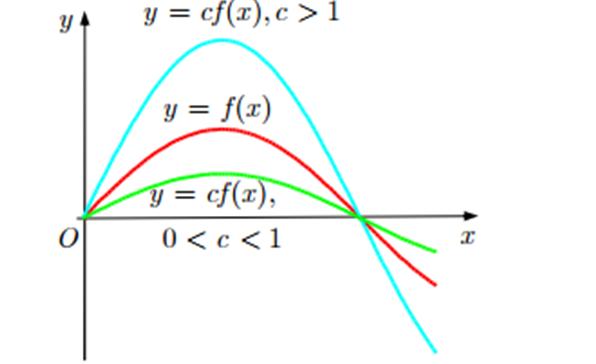
Рис. 2.4. Сжатия (растяжения) графика функции вдоль оси Oy
2.3. ОтражениеЗеркальное отражение относительно оси абсцисс
Для тех же значений x функции f(x) и -f(x) приобретают противоположных значений.
Поэтому для каждого
допустимого значения 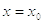 точка
точка 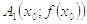 , что принадлежит
графику
, что принадлежит
графику  симметрична
относительно оси Ox точке
симметрична
относительно оси Ox точке 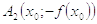 ()),
принадлежащей графику
()),
принадлежащей графику 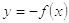 .
.
Графики функций  и
и 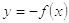 симметричны
относительно оси Ox.
симметричны
относительно оси Ox.
Итак, чтобы построить
график 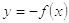 , график
, график  симметрично
отображают относительно оси Ox.
симметрично
отображают относительно оси Ox.
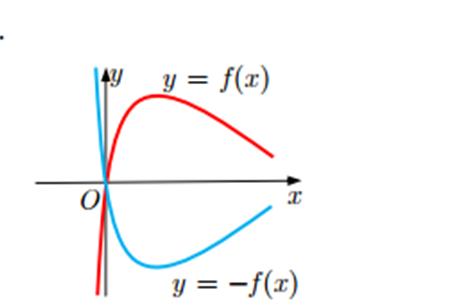
Рис. 2.5. Зеркальное отражение графика функции относительно оси абсцисс
Зеркальное отражение относительно оси ординат
Функция 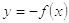 приобретает
те же значений, что и функция
приобретает
те же значений, что и функция  но
для противоположных значений x. К примеру, для
но
для противоположных значений x. К примеру, для 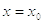 значение фунции
значение фунции 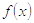 равна
равна 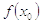 ; функция
; функция 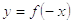 , также
приобретает значение
, также
приобретает значение 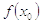 но для
но для 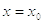 .
.
Поэтому для каждого
допустимого значения аргумента 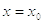 точка
точка
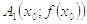 , что принадлежит
графику функции
, что принадлежит
графику функции 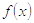 ,
симметричная относительно оси Oy точке
,
симметричная относительно оси Oy точке 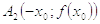 ,
принадлежащей графику функции
,
принадлежащей графику функции 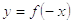 .
[5]
.
[5]
Графики функций  и
и 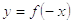 симметричны
относительно оси Oy.
симметричны
относительно оси Oy.
Чтобы построить график 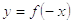 график
график  симметрично
отражают относительно оси Oy.
симметрично
отражают относительно оси Oy.
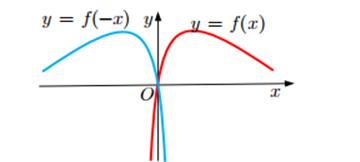
Рис. 2.6. Зеркальное отражение
2.4. Рекомендации по исследованию элементарных функций на уроках математикиРассмотрим примеры исследования элементарных функций на уроках математики
1) Функция y = f (x) +
b. График этой функции строится путем параллельного переноса графика функции y
= f (x) на вектор (0; b) вдоль оси ординат. Обозначим здесь и далее через 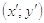
координаты точки, в которую переходит произвольная точка (x; y) координатной плоскости при данном преобразовании. [8]
Пусть f - произвольная функция с областью определения D (f). Выясним, в какую фигуру переходит график этой функции при данном переносе. Получаем, что произвольная точка имеет следующие координаты: (x; f (x) + b), где xєD (f).
Когда сам график сложный в построении перемещать его очень сложно, в таком случае целесообразнее вместо графика переносить оси. Так, для построения графику функции y = f (x) + b, надо переместить ось ОХ на вектор (0; -b).
Пример. Построим график функции: а) y = sin x + 2
В соответствии с правилом переносим график функции y = sin x на вектор (0, 2), то есть вверх по оси OY на 2 единицы (рис 2.7).
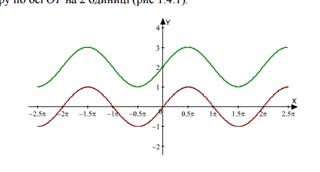
Рисунок 2.7. y = sin x + 2
2) Функция строится
графически путем растяжения графику функции y
= f (x) вдоль оси OY в k раз. Такое преобразование можно задать формулами:
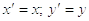
Для построения
точки M ", в которую переходит данная точка M при растяжении, надо построить на
прямой АМ, где А - проекция М на ось OХ, точку, ордината которой изменена в k
раз относительно ординаты точки M. На рисунке 2.8. показано построение точек, в
которые переходят данные при растяжениях с k 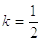 и
k=-2.
и
k=-2.

Рисунок 2.8.Переход точек
Пример: Построим графики
функций 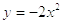 и
и 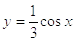 .
.
Построение осуществляется в первом случае из графика функции y = x2 (рис. 2.9), а в другом случае - с графика y=cosx (рис.2.10)
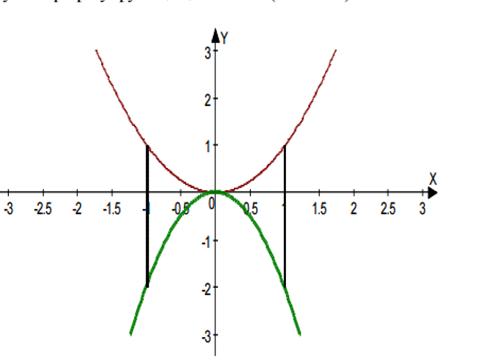
Рисунок 2.9. y = x2
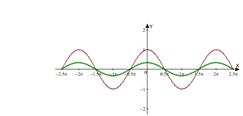
Рисунок 2.10 y=cosx
Рассматривая графики функций, содержащих модули, надо помнить как общие свойства модуля, так и правила отражения на координатной прямой.
Существуют функции, которые содержат переменную не только под знаком модуля. графики такого типа строят, рассматривая функцию на интервалах, где функция имеет постоянный знак (Методом интервалов). [2]
Алгоритм и особенности схематической построения графиков дробно-рациональной функции:
1. Определим область определения функции (D (y)), нули знаменателя будут точками, через которые проходят вертикальные асимптоты или точками разрыва графика, если такой же корень имеет числитель.
2. Найдем нули числителя, они будут нулями заданной функции.
3. Определим промежутки знакопостоянства и поведение функции на этих промежутках и при приближении аргумента к точкам разрыва и к ± ∞.
4. Учитывая полученные результаты, схематично строим график функции.
Заключение
В данной научно исследовательской работе рассмотрены способы схематической построенияграфиков сложных функций с помощью преобразования плоскости и анализасвойств составляющих функции.
Выполнив построение графиков сложных функций различных типов (от графиков смодулем, графиков дробно-рациональных функций), я пришел к выводу, что знаниязакономерностей между зависимыми функциями позволяют получить наглядную картину,определить поведение функции и схематично построить ее график. Замечено, чтолюбая сложная функция является функцией одной или нескольких элементарных функций.
Поэтому пользуясь элементарными методами анализа функции и графическихпреобразований на координатной плоскости можно схематично строить графики различныхтипов сложных функций. [1]
При графическом построении функций главную роль должен был качественный анализ функции. Поэтому наоснове выполненных графических построений был определен следующий алгоритмисследование функции и построения графика:
1. Определение ОПФ функции и точек ее разрыва на координатной прямой.
2. Определение нулей функции (точек пересечения оси ОХ)
3. Определение четности и периодичности функции.
4. Определение промежутков знакопостоянства (используя нули и разрывыфункции).
5. Нахождение вертикальных, горизонтальных и наклонных асимптот.
6. Исследование
поведения функции при приближении к точкам разрыва и при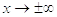 .
.
7. По данным анализа построить график функции.
Исследование функции нужно выполнять с одновременным схематичными очерками накоординатной плоскости (построением асимптот, точек пересечения осей, точек-экстремумов; обозначением промежутков возрастания и убывания, знакопостоянства). Далее,учтя все свойства функции, ОПФ и ОЗФ, проанализировав каждыйпромежуток, можно схематично строить график. Для улучшения точности графику,можно подкорректировать его на сомнительных участках, используя метод построенияграфике по точкам.
Для построения графика не обязательно использовать полный анализ функции,можно рассматривать только те свойства, которые имеют смысл для данной функции. Однакоможно прекращать анализ, не получив сформирован график.
Поэтому при построении графиков сложных функций были сформированы общие принципыанализа и построения графиков элементарными методами, что позволило более глубокопроникнуть в разнообразие графических изображений функций и их свойств.
При выполнении работы были достигнуты следующие результаты:
1) Выполняяпостроение различных графиков функций, были рассмотрены общие принципы исследованияфункции и построения их графиков;
2) было рассмотрено комплексное применение различныхметодов построения графиков функций;
3) Были рассмотрены сложные функции и выполненыпостроения соответствующих графиков.
4) Выполняя работу, были получены болееглубокие знания по анализу и графического построения функций.
Данная курсовая работа может быть использована учащимися, для получения дополнительныхзнаний относительно построения графиков функций и учителями математики при проведениифакультативных занятий.
Список использованной литературы
1. Амелькин В. Задачи з параметром: збірник задач / В. Амелькин — Минск, 1994. – 88 с.: ил..
2. Графики дробно-рациональной функции [Електронний курс]: arm-math.rkc- 74.ru – 1000кб – Доступ до режиму: arm-math.rkc-74.ru/DswMedia/grafikidrobnoracional-noyfunkcii.doc. 7. Графики и их функции [Електронний курс]: http://www.omsu.ru – 2300 кб – Доступ до режиму: http://www.omsu.ru/file.php?id=611
3. Лурьве М. В., Александров Б. И. Задачи на составление уравнений: Учеб. рук- во. — 3-е изд., перераб. / М. В. Лурьве, Б. И. Александров. — М.: Наука, 1990. — 96 с.
4. Махмутов М. Й. Проблемноє обучение. -М.: Педагогика, 1975. – 240 с.
5. Мордкович А. Г. Набольшее и наименьше значения величин. / А. Г. Мордкович. — М.: Школа-Пресс, 1995. — 144 с.
6. «Сложение графиков функций» [Електронний курс]: www.arm-math.rkc-74.ru – 808 кб – Доступ до режиму: www.arm-math.rkc-74.ru/DswMedia/grafikifunkciy.doc
7. Построение графиков сложных функций [Електронний курс]: http://festival.1september.ru – 352 кб – Доступ до режиму: http://festival.1september.ru/files/articles/52/5286/528629/pril.doc.
8. Шахно Г. У. «Сборник задач по элементарной математике повышенной трудности» / Г. У. Шахно. – Мінськ : «Высшая школа» 1965 р. – 523 с.: ил.
9. Шилов Г. Е. «Как строить графики» , збірник лекцій / Г. Е. Шилов. – Випуск 30 – Москва: ФИЗМАТГИЗ 1959. – 28 с.: ил.














 (zip - application/zip)
(zip - application/zip)











