Обработка результатов измерений

РХТУ им. Менделеева

                   Реферат на тему

 «Обработка результатов измерений»  

Требования, предъявляемые к методам обработки результатов прямых многократных независимых измерений устанавливаются ГОСТ Р 8.736-2011

Основные определения

Группа результатов измерений величин: Несколько результатов измерений (не менее четырех,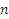

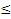4), полученных при измерениях одной и той же величины, выполненных с одинаковой тщательностью, одним и тем же средством измерений, одним и тем же методом и одним и тем же оператором.

Cистематическая погрешность измерения: систематическая погрешность: Составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины, проведенных с одинаковой тщательностью.

Грубая погрешность измерения: Погрешность измерения, существенно превышающая зависящие от объективных условий измерений значения систематической и случайной погрешностей.

Порядок обработки результатов измерений

При статистической обработке группы результатов прямых многократных независимых измерений выполняют следующие операции:

- исключают известные систематические погрешности из результатов измерений;

- вычисляют оценку измеряемой величины;

Оценку измеряемой величины 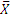, за которую принимают среднее арифметическое значение исправленных результатов измерений, вычисляют по формуле:

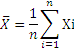
  где X_i   –  i-й результат измерений;

n  - число исправленных результатов измерений.

- вычисляют среднее квадратическое отклонение результатов измерений;

Среднее квадратическое отклонение S группы, содержащей n результатов измерений, вычисляют по формуле:

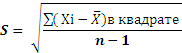
Среднее квадратическое отклонение среднего арифметического (оценки измеряемой величины) вычисляют по формуле:

                                                                            S_x =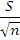 


- проверяют наличие грубых погрешностей и при необходимости исключают их;

Для исключения грубых погрешностей используют критерий Граббса. Статистический критерий Граббса исключения грубых погрешностей основан на предположении о том, что группа результатов измерений принадлежит нормальному распределению. Для этого вычисляют критерии Граббса G₁ и G₂, предполагая, что наибольший x_max или x_min наименьший результат измерений вызван грубыми погрешностями:

                                                      G₁ 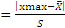  ,    G₂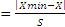

Сравнивают G₁ и G₂ с теоретическим значением G_T критерия Граббса при выбранном уровне значимости q. Таблица критических значений критерия Граббса приведена в приложении А.

Если 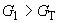, то X_max исключают как маловероятное значение. Если 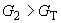, то X_min исключают как маловероятное значение. Далее вновь вычисляют среднее арифметическое и среднее квадратическое отклонения ряда результатов измерений и процедуру проверки наличия грубых погрешностей повторяют.

Если 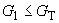, то X_max не считают промахом и его сохраняют в ряду результатов измерений. Если 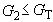, то X_min не считают промахом и его сохраняют в ряду результатов измерений.

- проверяют гипотезу о принадлежности результатов измерений нормальному распределению;

Проверку гипотезы о том, что результаты измерений принадлежат нормальному распределению, проводят с уровнем значимости q от 10% до 2%. Конкретные значения уровней значимости должны быть указаны в конкретной методике измерений.

- вычисляют доверительные границы случайной погрешности (доверительную случайную погрешность) оценки измеряемой величины;

Доверительные границы случайной погрешности оценки измеряемой величины в соответствии с настоящим стандартом устанавливают для результатов измерений, принадлежащих нормальному распределению.

При невыполнении этого условия методы вычисления доверительных границ случайной погрешности должны быть указаны в методике измерений.

2. При числе результатов измерений n≤15 принадлежность их к нормальному распределению не проверяют. При этом вычисление доверительных границ случайной погрешности оценки измеряемой величины по методике, предусмотренной настоящим стандартом, допускается только в том случае, если заранее известно, что результаты измерений принадлежат нормальному распределению.

Примечание - Если не известно распределение погрешностей оценки искомой величины, способы нахождения доверительных границ случайной погрешности могут быть указаны в методике измерений с учетом того, что подобные измерения повторяют.

3. При числе результатов измерений 15

4. При числе результатов измерений n>50 для проверки принадлежности их к нормальному распределению предпочтителен один из критериев:χ² К.Пирсона или ω² Мизеса-Смирнова. Критерий К.Пирсона приведен в приложении В, критерий Мизеса-Смирнова - в приложении Г.

5. Доверительные границы (без учета знака) случайной погрешности оценки измеряемой величины вычисляют по формуле

                                                               

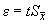
где - коэффициент Стьюдента, который в зависимости от доверительной вероятности и числа результатов измерений находят по таблице, приведенной в приложении Д, ГОСТ Р 8.736-2011.