Федеральное государственное бюджетное образовательное учреждение
высшего образования.
"ЧУВАШСКАЯ ГОСУДАРСТВЕННАЯ
СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ"
Инженерный факультет
Кафедра "Технического сервиса"
Курсовая работа по дисциплине
"Метрология стандартизации и сертификации"
на тему:
Обработка результатов
прямых многократных измерений
Выполнил: студент 2-ого курса
инженерного факультета
группа НТ-211
Григорьев А.В
Проверил: Лебедев В.Г
Чебоксары 2016 г.
 ВВЕДЕНИЕ
ВВЕДЕНИЕ
Целью измерений, как правило, является нахождение результата, наиболее близкого к истинному значению. Однако даже при использовании самых совершенных средств и методов измерений результат всегда будет содержать некоторую погрешность, источниками которой выступают условия измерений, применяемые инструменты и методы, индивидуальные особенности оператора и т.д.
Погрешности измерений могут быть уменьшены повышением точности средств измерений, совершенствованием и строгим соблюдением методик измерений и увеличением числа повторных измерений, т.е. многократными измерениями. Многократные измерения проводятся при поверке и калибровке средств измерений, при испытаниях изделий, при выполнении научных исследований, для характеристики случайных величин и т.д.
Обработка результатов многократных измерений представляет собой статистическую обработку определенной совокупности случайных величин, предположительно распределенных по нормальному закону. Задача обработки результатов сводится к оценке измеряемой величины и возможных границ ее нахождения при заданной доверительной вероятности.
Методика обработки результатов многократных измерений стандартизована, однако в зависимости от числа результатов отдельные этапы этой методики существенно различаются. В данном учебном пособии рассмотрена общая последовательность обработки результатов многократных измерений, приведены примеры расчетов для различных случаев, включая использование табличного процессора EXCEL, в приложении приведены необходимые справочные материалы.
 2 Обработка результатов наблюдений
при 15≤ n ≤ 50
2 Обработка результатов наблюдений
при 15≤ n ≤ 50
2.1Формируем таблицу исходных данных (табл.3)
Таблица 3 – Результаты измерений
|
№ результата, |
Результаты измерений |
№ результата, |
Результаты измерений |
|
1 |
16,96 |
15 |
17,30 |
|
2 |
16,86 |
16 |
17,42 |
|
3 |
16,95 |
17 |
17,10 |
|
4 |
16,83 |
18 |
17,44 |
|
5 |
17,16 |
19 |
17,26 |
|
6 |
16,87 |
20 |
17,12 |
|
7 |
16,97 |
21 |
17,09 |
|
8 |
16,85 |
22 |
17,28 |
|
9 |
17,00 |
23 |
17,37 |
|
10 |
17,05 |
24 |
17,20 |
|
11 |
17,18 |
25 |
17,18 |
|
12 |
17,29 |
26 |
17,01 |
|
13 |
17,18 |
27 |
17,45 |
|
14 |
16,99 |
2.2 Исключение систематических погрешностей результатов измерений .
Переменную систематическую погрешность выявляем и исключаем графический метод. По оси ординат графика (рисунок 2) откладываем результаты наблюдений в порядке их получения , по оси абцисс – порядковый номер результата.
Полученные точки соединяем ломаной линией. По характеру зависимости выбираем линейную аппроксимирующую функцию вида

где 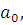
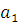 -постоянные коэффициенты ;
-постоянные коэффициенты ;
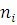 - порядковый номер результата
измерений.
- порядковый номер результата
измерений.
Значения
коэффициентов  и
и 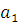 вычисляем методом наименьших
квадратов по формулам :
вычисляем методом наименьших
квадратов по формулам :
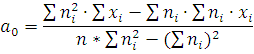
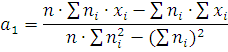
 |
Для расчета коэффициентов регрессии составляем вспомогательную таблицу 4.
Таблица 4 – Исходные данные для расчета коэффициентов регрессии
|
Исходные данные |
|
|
|
|
№ результата ( |
Результаты измерений ( |
||
|
1 |
16,96 |
16,96 |
1 |
|
2 |
16,86 |
33,72 |
4 |
|
3 |
16,95 |
50,85 |
9 |
|
4 |
16,83 |
67,32 |
16 |
|
5 |
17,16 |
85,80 |
25 |
|
6 |
16,87 |
101,22 |
36 |
|
7 |
16,97 |
118,79 |
49 |
|
8 |
16,85 |
134,80 |
64 |
|
9 |
17,00 |
153,00 |
81 |
|
10 |
17,05 |
170,50 |
100 |
|
11 |
17,18 |
188,98 |
121 |
|
12 |
17,29 |
207,48 |
144 |
|
13 |
17,18 |
223,34 |
169 |
|
14 |
16,99 |
237,86 |
196 |
|
15 |
17,30 |
259,50 |
225 |
|
16 |
17,42 |
278,72 |
256 |
|
17 |
17,10 |
290,70 |
289 |
|
18 |
17,44 |
313,92 |
324 |
|
19 |
17,26 |
327,94 |
361 |
|
20 |
17,12 |
342,40 |
400 |
|
21 |
17,09 |
358,89 |
441 |
|
22 |
17,28 |
380,16 |
484 |
|
23 |
17,37 |
399,51 |
529 |
|
24 |
17,20 |
412,80 |
576 |
|
25 |
17,18 |
429,50 |
625 |
|
26 |
17,01 |
442,26 |
676 |
|
27 |
17,45 |
471,15 |
729 |
|
|
|
|
|

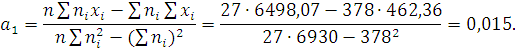
 Таким образом, зависимость изменения
результата измерения от времени может быть выражена функцией :
Таким образом, зависимость изменения
результата измерения от времени может быть выражена функцией :
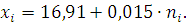
Для того, чтобы определить тесноту связи между рассматриваемыми величинами , необходимо вычислить коэффициент корреляции по формуле:
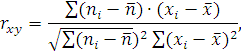
где 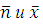 - среднее значение рассматриваемых
велечин.
- среднее значение рассматриваемых
велечин.
Для расчета коэффициента корреляции составляем вспомогательную таблицу 5.
Таблица 5 – исходные данные для расчета коэффициента корреляции
|
|
|
|
|
|
|
|
|
1 |
16,96 |
-13,00 |
-0,16 |
2,08 |
169,00 |
0,0256 |
|
2 |
16,86 |
-12,00 |
-0,26 |
3,12 |
144,00 |
0,0676 |
|
3 |
16,95 |
-11,00 |
-0,17 |
1,87 |
121,00 |
0,0289 |
|
4 |
16,83 |
-10,00 |
-0,29 |
2,90 |
100,00 |
0,0841 |
|
5 |
17,16 |
-9,00 |
0,04 |
-0,36 |
81,00 |
0,0016 |
|
6 |
16,87 |
-8,00 |
-0,25 |
2,00 |
64,00 |
0,0625 |
|
7 |
16,97 |
-7,00 |
-0,15 |
1,05 |
49,00 |
0,0225 |
|
8 |
16,85 |
-6,00 |
-0,27 |
1,62 |
36,00 |
0,0729 |
|
9 |
17,00 |
-5,00 |
-0,12 |
0,60 |
25,00 |
0,0144 |
|
10 |
17,05 |
-4,00 |
-0,07 |
0,28 |
16,00 |
0,0049 |
|
11 |
17,18 |
-3,00 |
0,06 |
-0,18 |
9,00 |
0,0036 |
|
12 |
17,29 |
-2,00 |
0,17 |
-0,34 |
4,00 |
0,0289 |
|
13 |
17,18 |
-1,00 |
0,06 |
-0,06 |
1,00 |
0,0036 |
|
14 |
16,99 |
0,00 |
-0,13 |
0,00 |
0,00 |
0,0169 |
|
15 |
17,30 |
1,00 |
0,18 |
0,18 |
1,00 |
0,0324 |
|
16 |
17,42 |
2,00 |
0,30 |
0,60 |
4,00 |
0,09 |
|
17 |
17,10 |
3,00 |
-0,02 |
-0,06 |
9,00 |
0,0004 |
|
18 |
17,44 |
4,00 |
0,32 |
1,28 |
16,00 |
0,1024 |
|
19 |
17,26 |
5,00 |
0,14 |
0,70 |
25,00 |
0,0196 |
|
20 |
17,12 |
6,00 |
0,00 |
0,00 |
36,00 |
0 |
|
21 |
17,09 |
7,00 |
-0,03 |
-0,21 |
49,00 |
0,0009 |
|
22 |
17,28 |
8,00 |
0,16 |
1,28 |
64,00 |
0,0256 |
|
23 |
17,37 |
9,00 |
0,25 |
2,25 |
81,00 |
0,0625 |
|
24 |
17,20 |
10,00 |
0,08 |
0,80 |
100,00 |
0,0064 |
|
25 |
17,18 |
11,00 |
0,06 |
0,66 |
121,00 |
0,0036 |
|
26 |
17,01 |
12,00 |
-0,11 |
-1,32 |
144,00 |
0,0121 |
|
27 |
17,45 |
13,00 |
0,33 |
4,29 |
169,00 |
0,1089 |
|
|
|
|
|
|
 Среднее значение
Среднее значение  определяются по формулам:
определяются по формулам:

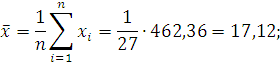
Коэффициент корреляции:
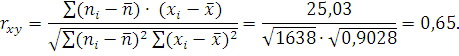
По величине коэффициента корреляции можно считать, что связь между результатом измерений и временем измерений существует сильная связь, т.е. в результатах измерений присутствует систематическая ошибка.
Для исключения систематических погрешностей в результаты измерений вводим поправку , определяемую по формуле:
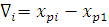
где  – расчетное значение результата
измерений, определенное по аппроксимирующей функции.
– расчетное значение результата
измерений, определенное по аппроксимирующей функции.
Исправленный результат измерений определяется по формуле :

Для вычислений исправленного результата составляем таблицу 6. Расчетные значения результатов измерений вычисляем по определенной выше аппроксимирующей функции
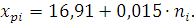
 Таблица 6 – Расчет исправленных
измерений
Таблица 6 – Расчет исправленных
измерений
|
№ п.п. |
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
16,96 |
17,075 |
0 |
16,96 |
|
2 |
16,86 |
17,09 |
0,02 |
16,84 |
|
3 |
16,95 |
17,105 |
0,04 |
16,91 |
|
4 |
16,83 |
17,12 |
0,06 |
16,77 |
|
5 |
17,16 |
17,135 |
0,08 |
17,08 |
|
6 |
16,87 |
17,15 |
0,10 |
16,77 |
|
7 |
16,97 |
17,165 |
0,12 |
16,85 |
|
8 |
16,85 |
17,18 |
0,14 |
16,71 |
|
9 |
17,00 |
17,195 |
0,16 |
16,84 |
|
10 |
17,05 |
17,21 |
0,18 |
16,87 |
|
11 |
17,18 |
17,225 |
0,20 |
16,98 |
|
12 |
17,29 |
17,24 |
0,22 |
17,07 |
|
13 |
17,18 |
17,255 |
0,24 |
16,94 |
|
14 |
16,99 |
17,27 |
0,26 |
16,73 |
|
15 |
17,30 |
17,285 |
0,28 |
17,02 |
|
16 |
17,42 |
17,3 |
0,30 |
17,12 |
|
17 |
17,10 |
17,315 |
0,32 |
16,78 |
|
18 |
17,44 |
17,075 |
0,34 |
17,1 |
|
|
17,26 |
17,09 |
0,36 |
16,9 |
|
20 |
17,12 |
17,105 |
0,38 |
16,74 |
|
21 |
17,09 |
17,12 |
0,40 |
16,69 |
|
22 |
17,28 |
17,135 |
0,42 |
16,86 |
|
23 |
17,37 |
17,15 |
0,44 |
16,93 |
|
24 |
17,20 |
17,165 |
0,46 |
16,74 |
|
25 |
17,18 |
17,18 |
0,48 |
16,7 |
|
26 |
17,01 |
17,195 |
0,50 |
16,51 |
|
27 |
17,45 |
17,21 |
0,52 |
17,45 |
Полученные данные исправленных результатов наносим на график (рис. 2) и используем в дальнейших расчетах.

Рисунок 2- Графический метод исключения систематических погрешностей.
2.3Оценка измеряемой величины.
Для удобства последующих расчетов составляем вариационный ряд исправленных результатов (табл. 7).
Таблица 7- Упорядоченная совокупность результатов наблюдений, мм
|
№ результата |
Результаты наблюдений |
Вариационный ряд |
№ результата |
Результаты наблюдений |
Вариационный ряд |
|
1 |
16,96 |
16,83 |
15 |
17,30 |
17,16 |
|
2 |
16,86 |
16,85 |
16 |
17,42 |
17,18 |
|
3 |
16,95 |
16,86 |
17 |
17,10 |
17,18 |
|
4 |
16,83 |
16,87 |
18 |
17,44 |
17,18 |
|
5 |
17,16 |
16,95 |
19 |
17,26 |
17,2 |
|
6 |
16,87 |
16,96 |
20 |
17,12 |
17,26 |
|
7 |
16,97 |
16,97 |
21 |
17,09 |
17,28 |
|
8 |
16,85 |
16,99 |
22 |
17,28 |
17,29 |
|
9 |
17,00 |
17 |
23 |
17,37 |
17,3 |
|
10 |
17,05 |
17,01 |
24 |
17,20 |
17,37 |
|
11 |
17,18 |
17,05 |
25 |
17,18 |
17,42 |
|
12 |
17,29 |
17,09 |
26 |
17,01 |
17,44 |
|
13 |
17,18 |
17,1 |
27 |
17,45 |
17,45 |
|
14 |
16,99 |
17,12 |

Среднее арифметическое значение вычисляем по формуле:
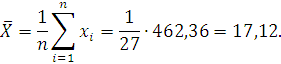
Среднеквадратическое отклонение вычисляем по формуле:
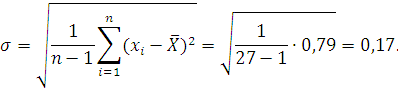
Среднеквадратическое отклонение среднего арифметического значения результата измерения определяется по формуле:
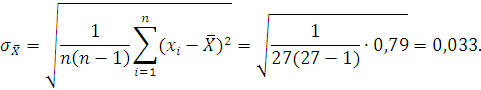
2.4 Обнаружение и исключение промахов из результата измерений.
Вычисляем критерии Граббса G1 и G2 , предполагая, что наибольший xmax или наименьший xmin результат измерений вызван грубыми погрешностями:

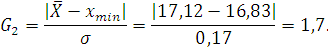
По таблице П1 приложений определяем табличное значение критерия Граббса при уровне значимости q=0,05:GT=2,822.
Так как 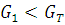 и
и 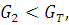 принимаем, что все результаты
измернеий должны быть сохранены в ряду результатов.
принимаем, что все результаты
измернеий должны быть сохранены в ряду результатов.
Критерий Ирвина. Определяем значения критерия Ирвина по формулам:
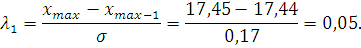

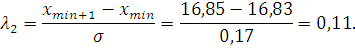
По таблице П2 приложений определяем табличное значение
критерия Ирвина при уровне значимости q=0,05: 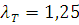 .
.
Так как 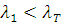 и
и 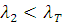 , принимаем, что результаты измерений
не содержат грубые погрешности.
, принимаем, что результаты измерений
не содержат грубые погрешности.
Критерий
Романовского. Определяем значения критерия Романовского для 
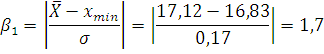
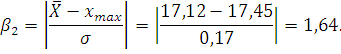
По таблице
П3 приложений определяем табличное значение критерия Романовского при уровне
значимости q=0,05: .
.
Так как 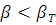 принимаем, что результат
принимаем, что результат 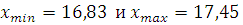 не являются грубыми погрешностями.
не являются грубыми погрешностями.
Критерий
Райта (3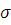 ). Проверяем результаты
). Проверяем результаты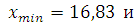
 на возможность грубой погрешности.
на возможность грубой погрешности.

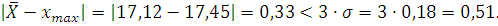
Результаты  и
и 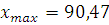 являются достоверными.
являются достоверными.
Критерий Диксона. Рассчитываем коэффициенты Диксона:
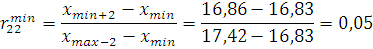

 По таблице П5 приложений определяем
табличное значения критерия Диксона при уровне значимости q=0,05:
По таблице П5 приложений определяем
табличное значения критерия Диксона при уровне значимости q=0,05: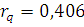 . Так как выполняются условия:
. Так как выполняются условия:
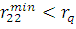 и
и 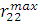 <
<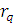 ,
,
считаем, что рассматриваемая совокупность не содержит грубых погрешностей.
2.5 Проверка гипотезы о принадлежности результатов измерений нормальному распределению .
При числе результатов измерений 15≤ n ≤ 50 нормальность распределения проверяют с помощью составного критерия.
Для расчета составного критерия составляем вспомогательную таблицу 8.
Таблица 8- Расчет составного критерия.
|
|
|
|
|
|
16,83 |
-0,29 |
-0,29 |
0,08 |
|
16,85 |
-0,27 |
-0,27 |
0,07 |
|
16,86 |
-0,26 |
-0,26 |
0,06 |
|
16,87 |
-0,25 |
-0,25 |
0,06 |
|
16,95 |
-0,17 |
-0,17 |
0,02 |
|
16,96 |
-0,16 |
-0,16 |
0,02 |
|
16,97 |
-0,15 |
-0,15 |
0,02 |
|
16,99 |
-0,13 |
-0,13 |
0,01 |
|
17 |
-0,12 |
-0,12 |
0,01 |
|
17,01 |
-0,11 |
-0,11 |
0,01 |
|
17,05 |
-0,07 |
-0,07 |
0,00 |
|
17,09 |
-0,03 |
-0,03 |
0,00 |
|
17,1 |
-0,02 |
-0,02 |
0,00 |
|
17,12 |
0 |
0 |
0,00 |
|
17,16 |
0,04 |
0,04 |
0,00 |
|
17,18 |
0,06 |
0,06 |
0,00 |
|
17,18 |
0,06 |
0,06 |
0,00 |
|
17,18 |
0,06 |
0,06 |
0,00 |
|
17,2 |
0,08 |
0,08 |
0,00 |
|
17,26 |
0,14 |
0,14 |
0,01 |
|
17,28 |
0,16 |
0,16 |
0,02 |
|
17,29 |
0,17 |
0,17 |
0,02 |
|
17,3 |
0,18 |
0,18 |
0,03 |
|
17,37 |
0,25 |
0,25 |
0,06 |
|
17,42 |
0,3 |
0,3 |
0,09 |
|
17,44 |
0,32 |
0,32 |
0,10 |
|
17,45 |
0,33 |
0,33 |
0,10 |
|
|
|

Критерий 1. Вычисляем смещенное среднеквадратическое
отклонение 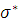 :
:
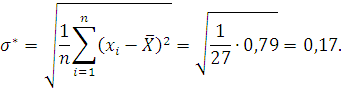
Определяем отношение 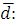

По таблице П6 приложений определяем квантили распределения при уровне значимости q=0,05:
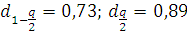
Так как выполняется условие

считаем, что результаты измерений в ряду распределены нормально.
Критерий 2. По таблице П7 приложенной для числа измерений n=25 при q=0,05 находим P=0,97. По таблице П8 приложений для P=0,97 находим zp/2=2,58,
тогда
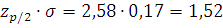
Из таблицы 8 находим ,что наибольшая разность (xi -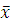 )= 0,31 т.е. m=0.
)= 0,31 т.е. m=0.
Таким образом, проверка по составному критерию показывает, что результаты измерений распределены нормально.
2.6 Доверительные границы случайной погрешности.
По таблице П12 приложений для доверительной вероятности P=0,05 определяем критическое значение коэффициента Стьюдента: tp=2,068
Абсолютная ошибка:

Нижняя доверительная граница:
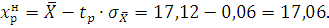
Верхняя доверительная граница:
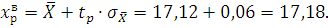
Доверительный интервал:
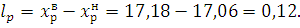
2.7 Форма записи оценки измеряемой величины.
Результат измерений записывается в виде:
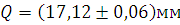 при P=0,95
при P=0,95
что
означает: результат измерений с вероятностью 0,95 находится в интервале от мм до
мм до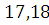 мм.
мм.
 3 Обработка результатов наблюдений
при n> 50
3 Обработка результатов наблюдений
при n> 50
3.1 Результаты прямых многократных измерений представлены в таблице 9.
Таблица 9- Результаты измерений
|
№ п.п |
Результаты измерений |
№ п.п |
Результаты измерений |
|
1 |
105,7 |
27 |
104,0 |
|
2 |
108,7 |
28 |
105,6 |
|
3 |
105,9 |
29 |
103,9 |
|
4 |
105,8 |
30 |
103,9 |
|
5 |
107,2 |
31 |
105,6 |
|
6 |
105,8 |
32 |
105,6 |
|
7 |
105,2 |
33 |
103,7 |
|
8 |
104,8 |
34 |
105,3 |
|
9 |
107,8 |
35 |
104,3 |
|
10 |
106,9 |
36 |
104,3 |
|
11 |
106,0 |
37 |
104,9 |
|
12 |
105,3 |
38 |
105,0 |
|
13 |
104,9 |
39 |
104,9 |
|
14 |
105,7 |
40 |
103,7 |
|
15 |
105,5 |
41 |
106,4 |
|
16 |
105,3 |
42 |
103,6 |
|
17 |
105,0 |
43 |
104,6 |
|
18 |
104,6 |
44 |
104,4 |
|
19 |
106,0 |
45 |
102,6 |
|
20 |
106,1 |
46 |
105,4 |
|
21 |
105,9 |
47 |
104,3 |
|
22 |
106,5 |
48 |
104,0 |
|
23 |
105,3 |
49 |
102,8 |
|
24 |
103,9 |
50 |
104,8 |
|
25 |
104,0 |
51 |
104,3 |
|
26 |
104,1 |
52 |
104,4 |
 0
0
3.2 Исключение систематических погрешностей результатов измерений.
Выбираем аппроксимирующую функцию, имеющую наибольшую коэффициент достоверности - полиномиальную функцию второй степени:
xi= 0,007n2 - 0,423n + 177,0
По величине достоверности аппроксимации R² = 0,675 принимаем, что в результатах измерений присутствует систематическая ошибка.
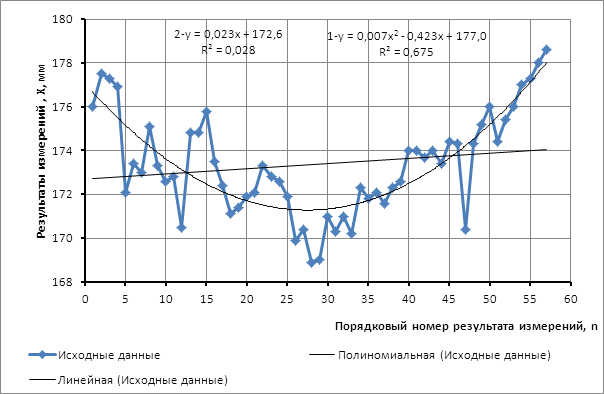
Рис.3. Выбор аппроксимирующей функции
Для исключения систематических погрешностей в результаты измерений вводим поправку, определяемую по формуле:
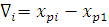
где  – расчетное значение результата
измерений, определенное по аппроксимирующей функции.
– расчетное значение результата
измерений, определенное по аппроксимирующей функции.
Исправленный результат измерений определяется по формуле :

Таблица 10 - Исключение переменной систематической погрешности.
|
Порядковый номер результата,ni |
Исходный результат измерений, |
Расчетное значение результата, |
Поправка |
Исправленный результат, |
|
1 |
2 |
3 |
4 |
5 |
|
1 |
105,7 |
176,58 |
||
|
2 |
108,7 |
176,18 |
||
|
3 |
105,9 |
175,79 |
||
|
4 |
105,8 |
175,42 |
||
|
5 |
107,2 |
175,06 |
||
|
6 |
105,8 |
174,71 |
||
|
7 |
105,2 |
174,38 |
||
|
8 |
104,8 |
174,06 |
||
|
9 |
107,8 |
173,76 |
||
|
10 |
106,9 |
173,47 |
||
|
11 |
106,0 |
173,19 |
||
|
12 |
105,3 |
172,93 |
||
|
13 |
104,9 |
172,68 |
||
|
14 |
105,7 |
172,45 |
||
|
15 |
105,5 |
172,23 |
||
|
16 |
105,3 |
172,02 |
||
|
17 |
105,0 |
171,83 |
||
|
18 |
104,6 |
171,65 |
||
|
19 |
106,0 |
171,49 |
||
|
20 |
106,1 |
171,34 |
||
|
21 |
105,9 |
171,20 |
||
|
22 |
106,5 |
171,08 |
||
|
23 |
105,3 |
170,97 |
||
|
24 |
103,9 |
170,88 |
||
|
25 |
104,0 |
170,8 |
||
|
26 |
104,1 |
170,73 |
||
|
27 |
104,0 |
170,68 |
||
|
28 |
105,6 |
170,64 |
||
|
29 |
103,9 |
170,62 |
||
|
30 |
103,9 |
170,61 |
||
|
31 |
105,6 |
170,61 |
||
|
32 |
105,6 |
170,63 |
||
|
33 |
103,7 |
170,66 |
||
|
34 |
105,3 |
170,71 |
||
|
35 |
104,3 |
170,77 |
||
|
36 |
104,3 |
170,84 |
||
|
37 |
104,9 |
170,93 |
||
|
38 |
105,0 |
171,03 |
||
|
39 |
104,9 |
171,15 |
||
|
40 |
103,7 |
171,28 |
||
|
41 |
106,4 |
171,42 |
||
|
42 |
103,6 |
171,58 |
||
|
43 |
104,6 |
171,75 |
||
|
44 |
104,4 |
171,94 |
||
|
45 |
102,6 |
172,14 |
||
|
46 |
105,4 |
172,35 |
||
|
47 |
104,3 |
172,58 |
||
|
48 |
104,0 |
172,82 |
||
|
49 |
102,8 |
173,08 |
||
|
50 |
104,8 |
173,35 |
||
|
51 |
104,3 |
173,63 |
||
|
52 |
104,4 |
173,93 |
 |
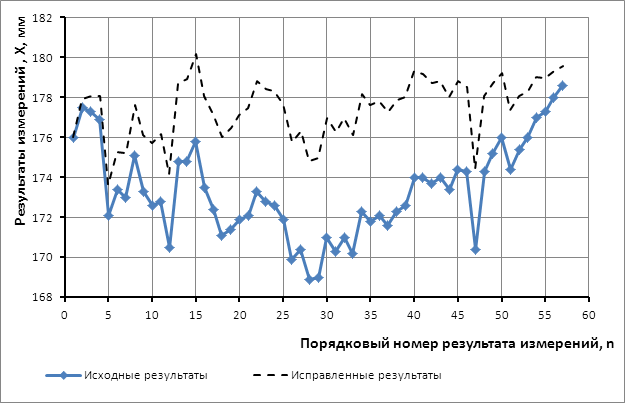

Рис.4. Исправленные результаты
3.3 Оценка измеряемой величины.
Среднее арифметическое значение результатов измерений:
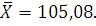
Среднеквадратическое отклонение:
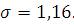
Среднеквадратическое отклонение среднего арифметического значения результатов измерений определяем по формуле:
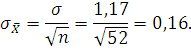
3.4 Обнаружение и исключение промахов из результата измерений.
Таблица 11- Упорядоченная совокупность результатов наблюдений, мм
|
№ результата |
Вариационный ряд |
№
|
Вариационный ряд |
№ результата |
Вариационный ряд |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
173,62 |
20 |
177,14 |
39 |
178,3 |
|
2 |
174,15 |
21 |
177,15 |
40 |
178,34 |
|
3 |
174,4 |
22 |
177,25 |
41 |
178,41 |
|
4 |
174,84 |
23 |
177,35 |
42 |
178,53 |
|
5 |
174,96 |
24 |
177,48 |
43 |
178,7 |
|
6 |
175,2 |
25 |
177,61 |
44 |
178,7 |
|
7 |
175,27 |
26 |
177,62 |
45 |
178,7 |
|
8 |
175,71 |
27 |
177,68 |
46 |
178,8 |
|
9 |
175,75 |
28 |
177,84 |
47 |
178,83 |
|
10 |
176 |
29 |
177,85 |
48 |
178,84 |
|
11 |
176,03 |
30 |
177,9 |
49 |
178,93 |
|
12 |
176,12 |
31 |
178,03 |
50 |
178,97 |
|
13 |
176,12 |
32 |
178,04 |
51 |
179,01 |
|
14 |
176,19 |
33 |
178,05 |
52 |
179,16 |
|
15 |
176,27 |
34 |
178,06 |
53 |
179,23 |
|
16 |
176,3 |
35 |
178,06 |
54 |
179,3 |
|
17 |
176,49 |
36 |
178,06 |
55 |
179,32 |
|
18 |
176,95 |
37 |
178,09 |
56 |
179,55 |
|
19 |
176,97 |
38 |
178,17 |
57 |
180,15 |
Критерий Райта 3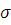 . Проверяем результаты
. Проверяем результаты 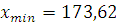 и
и 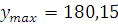 на возможность грубой погрешности.
на возможность грубой погрешности.
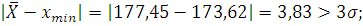
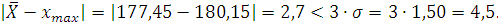
Результаты 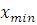 =
=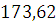 является
не достоверной погрешностью.
является
не достоверной погрешностью.
Критерий Ирвина. Определяем значения критерия Ирвина по формулам:
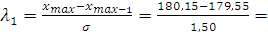 0,4;
0,4;

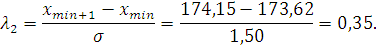
По таблице
П2 приложений определяем табличное значение критерия Ирвина при уровне
значимости q=0,05:  .
.
Так как 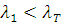 и
и 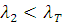 , принимаем, что результаты измерений
не содержат грубых погрешностей.
, принимаем, что результаты измерений
не содержат грубых погрешностей.
Критерий Смирнова. Наблюдаемые значения критерия при наименьшем и наибольшим результатах соответственно:
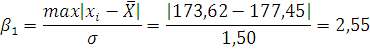

Предельное
значение критерия при уровне значимости q=0,05 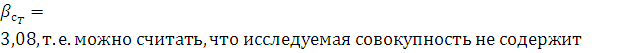 грубых погрешностей.
грубых погрешностей.
3.5 Проверка гипотезы о принадлежности результатов измерений нормальному распределению.
Проверку гипотезы по принадлежности результатов измерений нормальному распределению проведем с использованием критерия Пирсона.
Определяем число интервалов по формуле Стерджесса:
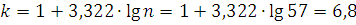
Принимаем k=7.
Ширина интервала определяется по условию:
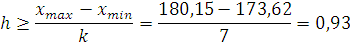
Принимаем h=0,94
Нижнюю границу первого интервала можно найти по выражению:

 Принимаем
Принимаем 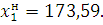
Верхнюю границу первого интервала определяем по формуле:
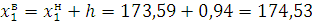
Середина первого определяется по формуле:
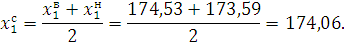
Для остальных интервалов параметры определяем аналогично и результаты сведем в таблицу 12.
Таблица 12- Параметры интервалов.
|
№ интервала |
Нижняя граница |
Верхняя граница |
Средина интервала |
|
1 |
173,59 |
174,53 |
174,06 |
|
2 |
174,53 |
175,47 |
175 |
|
3 |
175,47 |
176,41 |
175,94 |
|
4 |
176,41 |
177,35 |
176,88 |
|
5 |
177,35 |
178,29 |
177,82 |
|
6 |
178,29 |
179,23 |
178,76 |
|
7 |
179,23 |
180,17 |
179,7 |
 Для вычисления критерия Пирсона
составляем вспомогательную таблицу 13.
Для вычисления критерия Пирсона
составляем вспомогательную таблицу 13.
Таблица 13- Вспомогательная таблица для проверки распределения результатов измерений.
|
Номер интервала |
Середина интервала, |
Частота, |
|
|
|
|
|
1 |
174,06 |
3 |
-3,39 |
-2,3 |
0,028 |
1,0 |
|
2 |
175 |
4 |
-2,45 |
-1,6 |
0,110 |
3,9 |
|
3 |
175,94 |
9 |
-1,51 |
1,00 |
0,242 |
8,6 |
|
4 |
176,88 |
7 |
-0,57 |
0,4 |
0,368 |
13,1 |
|
5 |
177,82 |
15 |
0,37 |
0,2 |
0,391 |
13,9 |
|
6 |
178,76 |
15 |
1,31 |
0,9 |
0,266 |
9,5 |
|
7 |
179,7 |
4 |
2,25 |
1,5 |
0,129 |
4,6 |
Значения центрированной нормированной функции Лапласа находим по таблице П9 приложений.
При
расчете критерия Пирсона 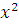 необходимо, чтобы частота в каждом
интервале была не менее 5, при этом допускается объединение соседних
интервалов, в которых
необходимо, чтобы частота в каждом
интервале была не менее 5, при этом допускается объединение соседних
интервалов, в которых 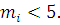 Число укрупненных интервалов должно
быть не менее 4.
Число укрупненных интервалов должно
быть не менее 4.
В нашем случае в первом интервале частота менее 5, т.е. необходимо объединить первые два интервала и шестой седьмым расчет критерия Пирсона выполнить по укрупненным интервалам.
Таблица 14- Расчет критерия Пирсона.
|
Номер интервала |
Опытная частота в укрупненных интервалах, |
Теоретическая частота в укрупненных интервалах, |
|
|
1 |
7 |
4,9 |
0,9 |
|
2 |
|||
|
3 |
9 |
8,6 |
0,02 |
|
4 |
7 |
13,1 |
2,84 |
|
5 |
15 |
13,9 |
0,08 |
|
6 |
19 |
14,1 |
1,7 |
|
7 |
|||
|
|

По таблице
П10 приложенной при числе степеней свободы 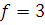 и уровне значимости q=0,1 определяем нижнее и верхнее
табличные значения критерия Пирсона:
и уровне значимости q=0,1 определяем нижнее и верхнее
табличные значения критерия Пирсона:
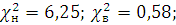
Следовательно, рассматриваемая совокупность результатов измерений подчиняется закону нормального распределения.
Теоретическую вероятность (дифференциальную функцию) определяем как разность интегральной функции для верхней и нижней границы интервала:

При этом в
принимаем 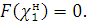
Теоретическая частота для каждого интервала определяется умножением дифференциальной функции на количество результатов измерений:

Таблица 15- Расчет критерия Пирсона .
|
|
|
|
|
|
|
|
|
|
|
1 |
174,53 |
3 |
0,026 |
0,026 |
1,5 |
7 |
5,3 |
0,54 |
|
2 |
175,47 |
4 |
0,093 |
0,067 |
3,8 |
|||
|
3 |
176,41 |
9 |
0,244 |
0,151 |
8,6 |
9 |
8,6 |
0,02 |
|
4 |
177,35 |
7 |
0,473 |
0,229 |
13,0 |
7 |
13 |
2,76 |
|
5 |
178,29 |
15 |
0,712 |
0,239 |
13,6 |
15 |
13,6 |
0,14 |
|
6 |
179,23 |
15 |
0,882 |
0,170 |
9,7 |
19 |
14,4 |
1,46 |
|
7 |
180,17 |
4 |
0,965 |
0,083 |
4,7 |
|||
|
|

Для
проверки гипотезы о нормальности распределения результатов измерений определяем
табличное значение критерия Пирсона с помощью мастера функций. В
рассматриваемом случае 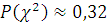 т. е. выполняются условия:
т. е. выполняются условия:

что означает нормальность распределения результатов измерений.
3.6 Доверительные границы случайной погрешности.
В рассматриваемом примере q=0,05 и n-1=56

Абсолютная ошибка:
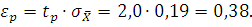
Нижняя доверительная граница:

Верхняя доверительная граница:
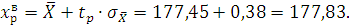
Доверительный интервал:
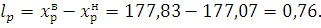
3.7 Форма записи оценки измеряемой величины.
Результат измерений записывается в виде:
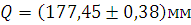 при P=0,95
при P=0,95
что
означает: результат измерений с вероятностью 0,95 находится в интервале от 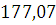 мм до
мм до  мм.
мм.
 Заключение.
Заключение.
При выполнении данной работы освоил методику обработки результатов прямых и многократных измерений.
 Литература.
Литература.
1. ГОСТ 8.376-2011. Государственная система обеспечения единства измерений. Измерения прямые многократные. Методы обработки результа- тов измерений. Общие положения. – М.: Стандартинформ, 2013. – 19 с.
2. Метрология, стандартизация и сертификация: учебник / А.И.Аристов, Л.И.Карпов, В.М.Приходько, Т.М.Раковщик. - М.: Издатель- ский центр «Академия», 2008. – 384 с.
3. Метрология, стандартизация и сертификация : учебное пособие / О.А. Леонов, В.В. Карпузов, Н.Ж. Шкаруба, Н.Е. Кисенков .- М. : КолосС, 2009. - 568 с.
4. Сергеев А.Г. Метрология, стандартизация и сертификация: учебник / А.Г.Сергеев, В.В.Терегеря. – М.: Издательство Юрайт; ИД Юрайт, 2010. – 820 с.
5. Метрология, стандартизация и сертификация: учебник / Ю.И.Борисов, А.С.Сигов, В.И.Нефедов и др; под ред. А.С.Сигова. – М.: ФО- РУМ, 2009. – 336 с.














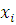
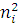

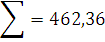
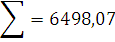
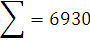
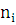

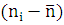
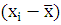
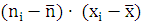
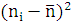
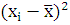
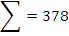

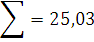
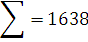
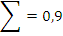

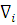
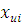
 19
19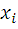
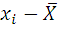

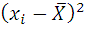
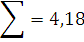
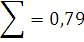
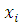
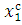
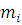
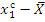
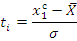

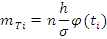
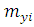

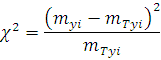
 5,54
5,54

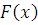
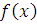
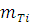

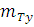
 (zip - application/zip)
(zip - application/zip)











