Нелинейные САУ

Московский Государственный Технический Университет им. Н.Э. Баумана

Курсовая работа по курсу “Нелинейные САУ”

на

тему:

Применение метода частотных круговых диаграмм к исследованию устойчивости систем с логическими алгоритмами управления.

Выполнил: ст-т гр. АК4-81

Смык В.Л.

Реутов 1997 г.

Применение метода частотных круговых диаграмм к исследованию устойчивости систем с логическими алгоритмами управления.

  На ранней стадии развития теории автоматического регулирования требование устойчивости работы системы было первым и обычно единственным и содержание большинства теоретических исследований сводилось к иследованию устойчивости.

  “Термин “устойчивость” настолько выразителен, что он сам за себя говорит”,-отмечают в начале изложения теории устойчивости Ж. Ла Салль и С. Лефшец [1]. Это вполне справедливо, но, несмотря на это, неточности и нелогичности можно встретить как раз не в математических, а в смысловых понятиях и терминах.

  Устойчивостью любого явления в обиходе называю его способность достаточно длительно и с достаточной точностью сохронять те формы своего существования, при утрате которых явление перестает быть самим сабой. Однако не только в обиходе, но и в научной терминалогии устойчивым называют не явление, а систему, в корой оно наблюдается, хотя это не оправдывает логически. Устойчивы ли физические тела - шар или куб? Такой вопрос будет иметь смысл, если речь идет о материале, из которого они сделаны. (Металлический шар

устойчив, шар из дыма нет.) Теорию управления интересует, однако, не эта прочнасная устойчивость. Подразумевается, что система управления как инженерная конструкция заведома устойчива, и в теории изучается устойчивость не самой системы, а ее состояний и функционирования. В одной и той же системе одни состояния или движения могут быть устойчивыми, а другие не устойчивыми. Более того, одно и то же жвижение может быть устойчивым относительно одной переменной и неустойцивым относительно другой - это отмечал еще А.М. Ляпунов [2]. Вращение ротора турбины устойчиво по отношению к угловой скорости и неустойчиво относительно угла поворота вала. Движение ракеты устойчиво относительно траектории и неустойчиво по отношению к неподвижной системе координат. Поэтому нужно оговаривать, устойчивость какого состояния или движения в системе и относительно каких переменных изучается. Так же есть много методов для оценки самой устойчивости. Мы рассмотрим как можно оценить устойчивость системы с логическим алгоритмом управления методом круговых диаграмм.

  Рассмотрим теоретическую часть и посмотрим что из себя представляет круговой критерий. Пусть дана система

                   . 

                   x=Ax+bx,   s=c^x,             (1)

 где x и s - в общем случае векторы (и, следовательно, b и с - прямоугольные матрицы), а матрица А не имеет собственных значений на линейной оси. Предположим , что для некоторого m, £ m £

система (1), дополненая соотношением x=-ms, асимптотически усойчива.

   Для абсолютной экпоненциальной устойчивости системы (1) в классе М() нелинейностей x=j(s,t), удовлетворяющих условию

       £ j(s,t)/s £                    (2)

достаточно, чтобы при всех w, -¥0, т.е. если нелинейные характеристики лежат в 1 и 3 квадрантах, и ее внешностью, если сектор () захватывает два смежных квадранта. Если одна из границ сектора совпадает с осью абсцисс, т.е. если =0 или =0 , то область С будет полуплоскостью, а ее граница - вертикальной прямой, проходящей соответственно через -1/ или -1/. На рисунке 1 показаны границы в плоскости z для различного расположения секторов () в плоскости s, x. Там же изображены кривые W(jw), w>0 для неособого случая, расположенные так, что возможна абсолютная устойчивость. Однако только приемлимого расположения хаоактеристик W(jw) еще недостаточно для суждения об абсолютной устойчивости : кроме этого, нужно еще потребовать, чтобы линейная замкнутоя система была асимптотически устойчивой.

  Круговой критерий обеспечивает также абсолютную устойчивость для системы с любым блоком, вход s и выход x которого удовлетворяют для всех t неравенству

     (s-x)(x-s)³0                            (7)  

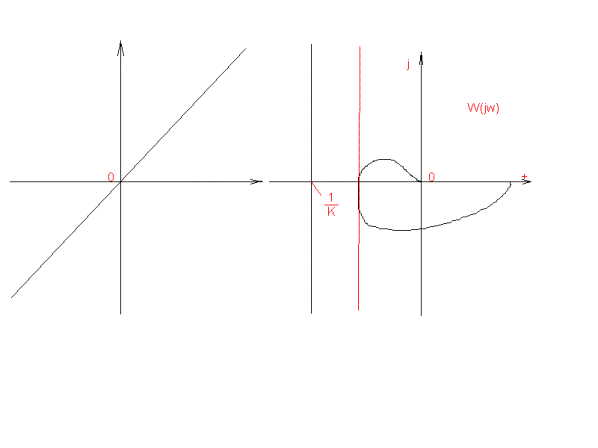
                   Рисунок 1, а.

Рассмотрим систему, приведенную на рис. 2.

           А          Х    Y    У  (P)         Z

              (-)          

                        G(p)      g

                          Рисунок 2.

  Здесь W(p) - оператор линейной части системы, которая может иметь в общем случае следущий вид:

            W(p)=;                

                                               (8)

         W(p)=;

  Алгоритм регулятора имеет вид:

              y=Yx,

              при gx>0          

      Y=                                     (9)

             - при gx0

       где    =

                   - k при g0,

а гадограф mW(jw)+1 при  соответствовал критерию Найквиста.

  Для исследуемой системы условие (3) удобнее записать в виде

(4) и (5).

  На рис. 4 приведенны возможные нелинейные характеристики из класса М() и годографы W(jw), расположенные таким образом, что согласно (4) и (5) возможна абсолютная устойчивость.

           y ^

                 y=g   ()   

                   |x|        y=g (при =0)           

                               >

                                                           0 

            “а”                                         “б”

            “в”                                         “г”

                     Рисунок 4.

 В рассматриваемом случае (10) при

               W(p)=, когда

         W(p)= W(p)G(p), G(p)=p+1,

 годограф W(jw) системы на рис. 5.

                            j                         

                                      W(jw)

                                    w=¥

                   >                                 (14)

 Интересно заметить, что достаточные условия абсолютной устойчивости по Ляпунову

         а > 0 , y(t) > 0

                 и

                 a > c

для рассматриваемого случая совпадают с достаточными условиями абсолютной устойчивости, полученными для кругового критерия (14), если выполняется требование

                 y(t) > 0                       (15)

поскольку, согласно (11) и (13)  a=a=.

    Докажем это, используя условия существования скользящего режима

       -k£y(t)=ck

т.е. подставим сюда вместо коэфициентов а,с, и k их выражения через

, , , тогда получим

       -£y(t)= £             (16)

Согласно рис. 5 и условия (16) получаем:

1) при  = , y(t)=0

2) при  > , y(t)>0

3) при  < , y(t) , то можно сделать вывод, что коректор будет влиять только на высоких частотах, а на низких будет преобладать , что можно наблюдать на графиках 1.1 - 1.4. На графиках 1.5 - 1.8 можно наблюдать минемальные значения , это значит что, при этих значениях будет максимальные значения полки нечувствительности релейного элемента.

   Минемальные значения полки нечуствительности можно наблюдать на графиках 1.9 - 1.12, особенно при минемальном значении  .

                   Приложение N 1.

   Программа для построения годографов на языке программирования

                         СИ ++.

#include

#include

#include

#include

#include

#include

#include

#include

void Godograf(float Tpr, float Ko, float Kos, int Color,

                             int Xc, int Yc, int x, int y, int z, int err);

void Osi(int Xc, int Yc, int kol);

int   xmax, ymax;

float Kos[]={0.1,1.0},

                  Ko[] ={10.0,100.0},

                  Tpr[]={0.01,0.09,0.2,0.5};

void main(void)

{

      float P_w, Q_w, w;

      int  driver, mode, err;

      driver = DETECT;

      initgraph(&driver,&mode,"");

      err = graphresult();

      if (err!=grOk) {cout