Моделирование морских экосистем

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное бюджетное государственное учреждение
Высшего профессионального образования
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГИДРОМЕТЕОРОЛОГИЧЕСКИЙ

УНИВЕРСИТЕТ

Кафедра промышленной океанологии и охраны природных вод

Курсовая работа
 по дисциплине
«Введение в сферу профессиональной деятельности»
на тему
«Моделирование морских экосистем»

Выполнил ст. О - 143
Новиков М.О.

Руководитель к.г.н. доц.
Чанцев В.Ю.

Санкт-Петербург
2016

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ. 3

БИОСФЕРА.. 4

Биогеохимические круговороты элементов. 6

Экологическая система. 10

ЗАКЛЮЧЕНИЕ. 16

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ.. 18

ВВЕДЕНИЕ

Экологическая система представляет собой сложное образование с разнокачественными характеристиками. Окружающая среда изучается как совокупность физико-химических процессов, живые компоненты устроены сложнее, здесь исследуются биологические процессы со своими закономерностями.

В области математического моделирования экологических систем наиболее длинный путь пройден для водных экосистем. Это связано с достаточно определенной структурой водных живых систем, известными направлениями переноса вещества в пространстве, сравнительно слабым влиянием неизвестных случайных факторов. Во всяком случае, этим водные экосистемы отличаются от наземных. Начало математическому моделированию водных экосистем положили математики и биологи в первой трети двадцатого века. Тогда изучали общие экологические модели. Видное место в моделировании водных экосистем занимает В.А.Костицын (Kostitzin, 1937). Он исследовал различные математические модели функционирования популяций и сообществ водных организмов в пресных водоемах. Дальнейшие исследования первой половины двадцатого века привели к большому количеству моделей популяций и сообществ водных организмов, а также созданию методологии моделирования водных экосистем. К 70 - 80-ым годам прошлого века были разработаны тысячи моделей для различных конкретных внутренних водоемов, морей и отдельных районов океанов [4].

БИОСФЕРА

На Земле живые организмы существуют в верхних слоях земной коры, гидросфере и атмосфере. Уже в XVIII в. в трудах Ламарка было сформировано понятие о тонкой оболочке жизни, покрывающей Землю, а 1920-х советский биогеохимик В. И. Вернадский  разработал учение о биосфере [1].

И. Вернадский считал, что биосфера есть особая наружная оболочка земной коры, занятая и преобразованная жизнью. Живые организмы  являются «...трансформаторами, переводящими космические излучения в действенную земную энергию - электрическую, химическую, тепловую...» [1]. Наш основной источник энергии - Солнце. Значит, биосфера является сложной термодинамически открытой системой, получающей энергию извне, часть которой идёт на работу, а часть рассеивается в виде тепла. От Солнца до поверхности Земли доходит только 52% энергии, из которой лишь 1% преобразуется растениями в живое вещество, А остальная энергия уходит на нагревание, испарение и другие физические процессы.

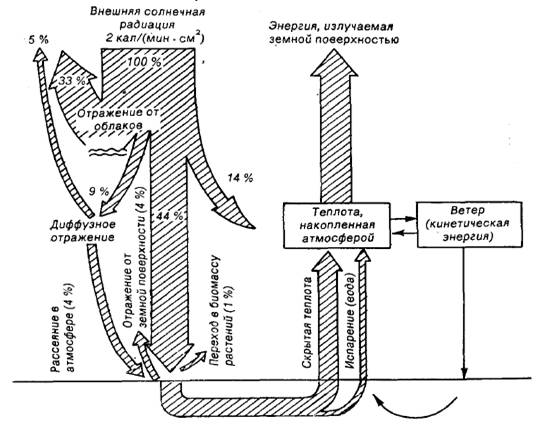
Рис. 1.1 Баланс солнечной энергии на земной поверхности.

Живое вещество содержит энергию, благодаря ей оно становится активным, собирает и распределяет в биосфере полученную в форме излучения энергию и превращает её в работу. Эта работа состоит в переносе и перераспределении химических элементов в биосфере, создании из них новых тел, из-за чего значительная часть атомов земной поверхности находится в непрерывном круговороте. Все почвы, минералы верхних слоёв земной коры и месторождения руд, углей и нефти образовались и продолжают образовываться под действием жизни; Химический состав природных вод в значительной мере сформирован живыми организмами.

Живое вещество биосферы распределяется по земной поверхности и оказывает влияние на окружающую среду, изменяя ее. С течением времени жизнь неизбежно покрывает весь земной шар и только временно может отсутствовать на определённых его участках. Это движение, приводящее к «вездесущности жизни», достигается путем размножения и перемещения организмов.

Пределы биосферы обусловлены границами физических условий существования живых организмов. Согласно современным представлениям, существование жизни ограничивается диапазоном значений температуры —250 - 160 °С и давления 0,001 - 3000 атм. Нижняя граница жизни в гидросфере условно проходит на глубине 10 км, в земной коре — до 2 км; верхняя граница распространения жизни в атмосфере обусловлена слоем озона, который предохраняет живую материю от ультрафиолетового излучения Солнца, и расположена на высоте около 45 км над уровнем моря.

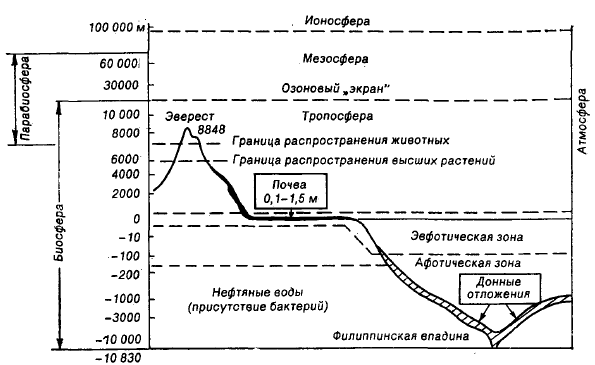
Рис 1.2 Схема строения биосферы.

Биогеохимические круговороты элементов

Несоответствие между наличием и доступностью химических элементов в земной коре, с одной стороны, и потребностями живых организмов, с другой, породило в биосфере проблему дефицита некоторых элементов и привело к ограничению продукции живого вещества. Единственным выходом из этого положения оказалось использование элементов по типу круговоротов, когда элемент, пройдя целый ряд биологических и химических превращений, входит в состав того же самого соединения, в котором он находился в начальный момент. В настоящее время биогенные элементы земной коры охвачены глобальными и локальными круговоротами, причем движущей силой в функционировании круговоротов являются живые организмы.

В формировании и специфике функционирования современных круговоротов элементов важнейшую роль сыграло накопление в атмосфере сильного окислителя — кислорода, который, в свою очередь, явился побочным продуктом жизнедеятельности фотосинтезирующих организмов. Так само живое вещество планеты стало мощной геологической силой, в значительной мере определившей своеобразие состояния земной коры, вод и атмосферы.

1.      Углерод. Движущей силой глобального круговорота углерода является биологический круговорот, протекающий по схеме: биоассимиляция углерода из атмосферы, водной или наземной среды растениями> потребление органических соединений животными > окисление органических веществ до углекислого газа в процессе дыхания и разложения отходов >-возврат углекислого газа (СО2)в атмосферу. Биологический круговорот углерода тесно связан с круговоротом кислорода, выделяемого и потребляемого организмами. Взаимодействие и противоположную направленность биологических составляющих этих круговоротов иллюстрирует Рис1.3.

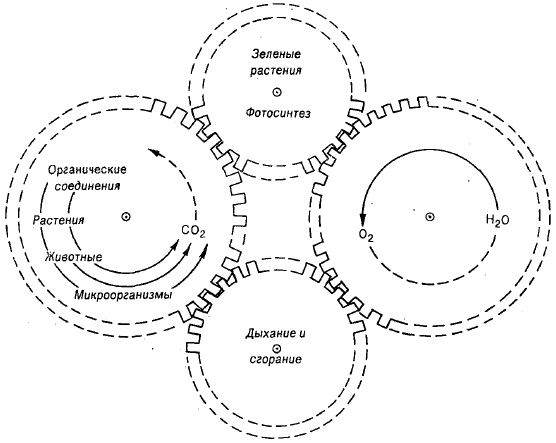
Рис 1.3 Взаимодействие циклов углерода и кислорода в биосфере.

2.       Азот. Азот в круговороте в целом следует за углеродом, вместе с которым участвует в образовании белковых структур, однако в силу химической специфики элементов круговороты углерода и азота имеют некоторые различия. Если углекислый газ из атмосферы могут потреблять все виды фотосинтетиков, то фиксацию атмосферного азота способны производить только некоторые виды бактерий, сине-зелёных водорослей и симбиотические бактерии бобовых. Второе отличие цикла азота от цикла углерода состоит в том, что при естественном разрушении органического вещества образуется не газообразный азот, а раствор нелетучих соединений азота. Вследствие этого, для замыкания круговорота азота до газообразного состояния необходимо участие нескольких специализированных групп микроорганизмов. Органические азотсодержащие вещества с помощью редуцентов микроорганизмов первоначально разлагаются с выделением аммиака. Далее нитрифицирующие бактерии окисляют аммиак до нитритов и нитратов, после чего в анаэробных условиях может происходить денитрификация до газообразного азота, осуществляемая денитрифицирующими бактериями.

3.      Фосфор. К круговоротам основных биогенных элементов, имеющих газовую фазу, примыкают так называемые осадочные круговороты, из которых важнейшим является круговорот фосфора. Минеральный фосфор — редкий элемент в биосфере, в земной коре его содержание не превышает 1 %. Основными источниками неорганического фосфора являются изверженные или осадочные породы. Неорганический фосфор из пород земной коры вовлекается в циркуляцию выщелачиванием и растворением в континентальных водах. В экосистемах суши неорганический фосфор поглощается растениями и переводится в состав живого вещества. Затем органические фосфаты вместе с трупами, отходами и выделениями живых существ возвращаются в почву, подвергаются переработке микроорганизмами и снова включаются в круговорот. В водные экосистемы фосфор приносится текучими водами в виде фосфатов. Если в наземных экосистемах круговорот фосфора происходит в оптимальных условиях с минимумом потерь на выщелачивание, то в водоемах дело обстоит далеко не так. Это связано с седиментацией отмерших организмов, фрагменты которых, не использованные детритофагами, накапливаются на дне водоемов. Вследствие пространственного разделения процесса образования кислорода в верхних слоях воды при фотосинтезе и его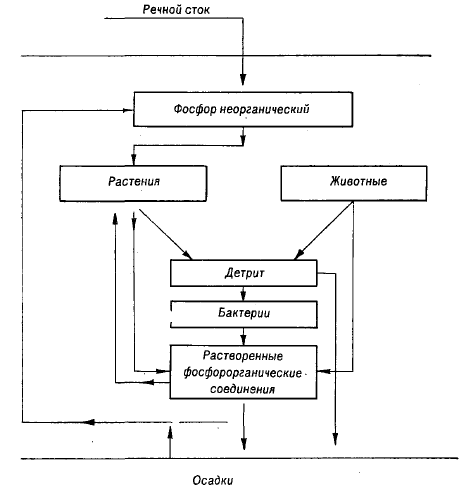

Рис. 1.4 Схема круговорота фосфора в океане.
потребления при деструкции органических веществ вблизи дна, аэробная деструкция вблизи дна несколько замедляется. Минерализованный фосфор в донных отложениях при аэробных условиях образует соединение с трехвалентным железом (FePO4), который еще менее растворим, чем гидроокись железа, и прочно удерживается в осадке. Во многих водоемах возврат фосфора из донных отложений осуществляется в основном только при сезонном перемешивании вод.

Экологическая система

Глобальные круговороты биогенных элементов распадаются в биосфере на множество мелких круговоротов, приуроченных к локальным местообитаниям различных биологических сообществ, образующих как бы части биосферы. Функциональные системы, включающие в себя сообщество живых организмов и среду их обитания, осуществляющие более или менее замкнутый круговорот биогенных элементов, называются экологическими системами.

Очевидно, что необходимость создания направленного потока энергии, с одной стороны, и круговорота веществ, с другой, налагает определенные ограничения на подбор видов, которые могут существовать в экосистеме. В основе любой, даже самой простой экосистемы лежит пищевая (трофическая) цепь. В плане экологического моделирования, различие между пастбищной и другими типами пищевых цепей состоит в том, что потребители детрита и паразиты не оказывают прямого влияния на численность популяций других организмов, отходы которых они потребляют, а между участниками пастбищной цепи осуществляется хищничество, приводящее к изменению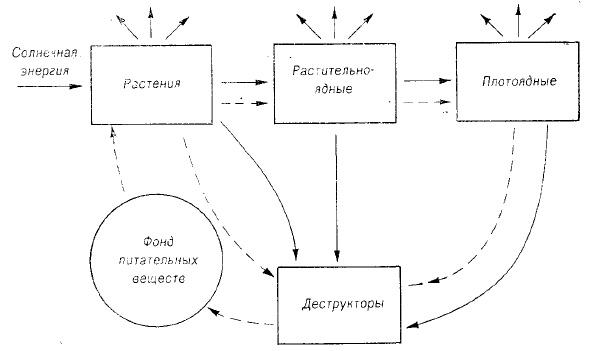

Рис. 1.5 Блоковая модель экосистемы.

численности популяций как выше, так и нижерасположенных трофических уровней. Таким образом, для стабилизации пастбищных цепей экосистем требуется более тонкая регулировка, осуществляемая обычно на основе отрицательных обратных связей [2].

МАТЕМАТИЧЕСКОЕ МОДЕЛИРВАНИЕ

Математическое моделирование - это средство изучения реального объекта, процесса или системы путем их замены математической моделью, более удобной для экспериментального исследования с помощью ЭВМ.

Математическая модель является приближенным представлением реальных объектов, процессов или систем, выраженным в математических терминах и сохраняющим существенные черты оригинала. Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи.

В общем случае математическая модель реального объекта, процесса или системы представляется в виде системы функционалов.

Ф i ( X , Y , Z , t )=0,

где X - вектор входных переменных, X =[ x 1 , x 2 , x 3 , ... , xN ] t ,

Y - вектор выходных переменных, Y =[ y 1, y 2, y 3, ... , yN ] t ,

Z - вектор внешних воздействий, Z =[ z 1, z 2, z 3, ... , zN ] t ,

t - координата времени.

Построение математической модели заключается в определении связей между теми или иными процессами и явлениями, создании математического аппарата, позволяющего выразить количественно и качественно связь между теми или иными процессами и явлениями, между интересующими специалиста физическими величинами, и факторами, влияющими на конечный результат.

Обычно их оказывается настолько много, что ввести в модель всю их совокупность не удается. При построении математической модели перед исследованием возникает задача выявить и исключить из рассмотрения факторы, несущественно влияющие на конечный результат (математическая модель обычно включает значительно меньшее число факторов, чем в реальной действительности). На основе данных эксперимента выдвигаются гипотезы о связи между величинами, выражающими конечный результат, и факторами, введенными в математическую модель. Такая связь зачастую выражается системами дифференциальных уравнений в частных производных (например, в задачах механики твердого тела, жидкости и газа, теории фильтрации, теплопроводности, теории электростатического и электродинамического полей).

Конечной целью этого этапа является формулирование математической задачи, решение которой с необходимой точностью выражает результаты, интересующие специалиста.

Форма и принципы представления математической модели зависит от многих факторов.

По принципам построения математические модели разделяют на :

• аналитические;

• имитационные.

В аналитических моделях процессы функционирования реальных объектов, процессов или систем записываются в виде явных функциональных зависимостей.

Аналитическая модель разделяется на типы в зависимости от математической проблемы:

• уравнения (алгебраические, трансцендентные, дифференциальные, интегральные),

• аппроксимационные задачи (интерполяция, экстраполяция, численное интегрирование и дифференцирование),

• задачи оптимизации,

• стохастические проблемы.

Однако по мере усложнения объекта моделирования построение аналитической модели превращается в трудноразрешимую проблему. Тогда исследователь вынужден использовать имитационное моделирование.

В имитационном моделировании функционирование объектов, процессов или систем описывается набором алгоритмов. Алгоритмы имитируют реальные элементарные явления, составляющие процесс или систему с сохранением их логической структуры и последовательности протекания во времени. Имитационное моделирование позволяет по исходным данным получить сведения о состояниях процесса или системы в определенные моменты времени, однако прогнозирование поведения объектов, процессов или систем здесь затруднительно. Можно сказать, что имитационные модели - это проводимые на ЭВМ вычислительные эксперименты с математическими моделями, имитирующими поведение реальных объектов, процессов или систем.

В зависимости от характера исследуемых реальных процессов и систем математические модели могут быть:

• детерминированные,

• стохастические.

В детерминированных моделях предполагается отсутствие всяких случайных воздействий, элементы модели (переменные, математические связи) достаточно точно установленные, поведение системы можно точно определить. При построении детерминированных моделей чаще всего используются алгебраические уравнения, интегральные уравнения, матричная алгебра.

Стохастическая модель учитывает случайный характер процессов в исследуемых объектах и системах, который описывается методами теории вероятности и математической статистики.

По виду входной информации модели разделяются на :

• непрерывные,

• дискретные.

Если информация и параметры являются непрерывными, а математические связи устойчивы, то модель - непрерывная. И наоборот, если информация и параметры - дискретны, а связи неустойчивы, то и математическая модель - дискретная.

По поведению моделей во времени они разделяются на :

• статические,

• динамические.

Статические модели описывают поведение объекта, процесса или системы в какой-либо момент времени. Динамические модели отражают поведение объекта, процесса или системы во времени.

По степени соответствия между математической моделью и реальным объектом, процессом или системой математические модели разделяют на
• изоморфные (одинаковые по форме),

• гомоморфные (разные по форме).

Модель называется изоморфной, если между нею и реальным объектом, процессом или системой существует полное поэлементное соответствие. Гомоморфной - если существует соответствие лишь между наиболее значительными составными частями объекта и модели [3].

ЗАКЛЮЧЕНИЕ

Математическое моделирование морских экосистем – это способ описания процессов и физико-химических закономерностей в этих самых системах с помощью языка математики для анализа последствий заданных в модели явлений. Задачи модельных исследований связаны с анализом закономерностей функционирования экосистем и сообществ, а также прогнозированием динамики основных параметров системы. Водные экосистемы чаще всего моделируются как динамические системы.

Модельное описание динамики водной экосистемы состоит из следующих блоков:

1) динамика водной массы (течения, другие перемещения);

2) изменение состояния водной среды вследствие физико-химических превращений;

3) динамика живой составляющей экосистемы – биологического сообщества.

В основе моделирования сообщества лежит трофическая структура. Например, может использоваться следующая схема (рис. 2).

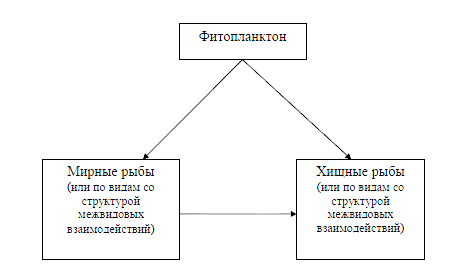
Рис. 2 Схема трофических взаимодействий в биологическом сообществе водных организмов.

Исследование любой природной системы в настоящее время невозможно без учета антропогенного воздействия, которому она в той или иной степени подвергается. Анализ последствий такого воздействия сложен, но важен с точки зрения развития и изменения природной системы. Такой анализ рационально проводить с помощью математических моделей - это дешевле других способов и не требует, как правило, дополнительного вторжения в природную среду [4].

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1.           Вернадский В. И. Биосфера (Изб. тр. по биогеохимии).— М.: Наука, 1967.—С. 3—23.

2.           Алексеев В. В., Крышев И. И., Сазыкина Т. Г. Физическое и математическое моделирование экосистем. – СПб.: Гидрометиздат, 1992.

3.         DMT Software, http://dmtsoft.ru/bn/305/as/oneaticleshablon.

4.         Абакумов А. И. Математическое моделирование водных экосистем: история, проблемы, перспективы. – Владивосток.: Институт автоматики и процессов управления ДВО РАН.