Модели радиоактивного заражения водоемов

МИНИСТЕРСТВО АГРАРНОЙ ПОЛИТИКИ И ПРОДОВОЛЬСТВИЯ УКРАИНЫ

КЕРЧЕНСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

Технологический факультет

Кафедра: Экологии моря

Реферат

По дисциплине: Моделирование и прогнозирование состояния окружающей среды

«Модели радиоактивного заражения водоемов»

Выполнила:

студентка группы ЭМ-3

Герасименко О. А.

Проверила: ассистент

Ошкадер А. В.

Керчь 2012

Радиоактивное заражение — это загрязнение местности и находящихся на ней объектов радиоактивными веществами. Причинрадиоактивного заражения несколько. Радиоактивное заражение происходит главным образом при:

-                    ядерном взрыве в результате выпадения радиоактивных веществ из облака ядерного взрыва и наведённой радиации, обусловленной образованием радиоактивных изотопов в окружающей среде под воздействием мгновенного нейтронного и гамма-излучений ядерного взрыва; поражает людей и животных главным образом в результате внешнего гамма- и (в меньшей степени) бета-облучения, а также в результате внутреннего облучения (в основном альфа-активными нуклидами) при попадании радиоизотопов в организм с воздухом, водой и пищей.

-                    техногенных авариях (утечках из ядерных реакторов, утечках при перевозке и хранении радиоактивных отходов, случайных утерях промышленных и медицинских радиоисточников и т. д.) в результате рассеяния радиоактивных веществ; характер заражения местности зависит от типа аварии.

Основные загрязняющие радиоактивные компоненты:

-                    Йод-131 (¹³¹I) — является бета- и гамма-радиоактивным, период полураспада — около 8 суток. В связи с бета-распадом, ¹³¹I вызывает мутации и гибель клеток, в которые он проник, а также — окружающих тканей на глубину нескольких миллиметров. Концентрируется в основном в щитовидной железе.

-                    Стронций-90 (⁹⁰Sr) — период полураспада — примерно 28,8 лет. В окружающую среду ⁹⁰Sr попадает преимущественно при выбросах с АЭС и ядерных взрывах. Крайне опасен. Откладывается, в основном, в костных тканях (костях).

-                    Цезий-137 (¹³⁷Cs) — период полураспада — 33 года. Один из главных компонентов радиоактивного загрязнения биосферы. Выброс ¹³⁷Cs в окружающую среду происходит в основном в результате аварий на предприятиях атомной энергетики и испытаний ядерного оружия.

-                    Кобальт-60 (⁶⁰Co) — период полураспада примерно равен 5,3 года.

-                    Америций-241 (²⁴¹Am) — период полураспада примерно равен 433 года.

При разработке модели распространения радиоактивного загрязнителя в экосистеме водоема встает очень важный и принципиальный вопрос: каким должен быть уровень моделирования процессов транспорта и накопления радионуклидов в компонентах водоема, т. е. каким образом надо разделить экосистему водоема на подсистемы, как учесть в модели связи между подсистемами, чтобы модель адекватно отображала реальные процессы в водоеме и удовлетворяла поставленным целям моделирования. Очевидно, что построения модели миграции радионуклидов в водоеме на популяционном уровне вполне достаточно, чтобы удовлетворить любым целям моделирования. Популяция — своеобразная единица экологического масштабирования то ответ о передаче радионуклидов от одной популяции к другой и накоплении радионуклидов в каждой популяции позволяет определить не только эффект воздействия радиоактивного загрязнителя на популяцию, но и на человека, контактирующего с данной популяцией. Естественно, что популяции в водоеме взаимодействуют с его абиотическими составляющими, поэтому в модели, построенной на популяционном уровне, должны присутствовать и эти компоненты.

Исходя из концепции модели на популяционном уровне в экосистеме водоема, необходимо определить виды гидробионтов, составляющих гидроценоз водоема, определить структуру трофических взаимодействий между популяциями этих видов, структуру взаимодействия популяций с абиотическими компонентами и внешними составляющими биосферы.

Общий подход к такому построению модели заключается в выделении в гидробиогеоценозе водоема функционально однородных групп гидробионтов, описывающих структуру трофических связей. Это известные группы (рис. 1):

-          автотрофы (продуценты) - хлорофиллоносные организмы растений (фитопланктон, водоросли, высшая водная растительность);

-          гетеротрофы (консументы) - организмы, питающиеся организмами растений или консументами более низкого уровня (хищники);

-          сапрофиты (деструкторы) — организмы (бактерии, грибки), разлагающие останки продуцентов и консументов при употреблении их в пищу.

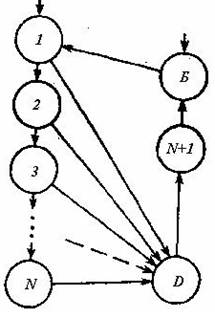
Рис. 1. Схема миграции радионуклидов в звеньях трофической цепи водоема (1 - продуценты; 2 - травоядные; 3 - консументы 1-го порядка; N - консументы i-го порядка; D - деструкторы; Б - биогены; N + 1 - индекс трофического уровня).

Эти группы, взаимодействуя с абиотическими компонентами, другими (сторонними) компонентами биосферы, потребляя энергию извне (солнечная энергия, биогенные элементы, поступающие в водоем из прибрежной зоны), определяют общую структуру экосистемы любого водоема и ее функционирование. Для конкретного водоема необходимо детализировать каждую из групп до уровня популяций. Это задача решаемая. Однако параметризация такой модели, т. е. опреде­ление параметров взаимосвязи популяций, - задача крайне сложная, а при отмеченных выше поступлениях и уровнях содержания радионуклидов в компонентах водоема практически нерешаемая: не уда­ется определить активность радионуклидов в каждой из популяций из-за ее малости. В то же время для решения задач санитарно-гигиенической охраны водоема модель транспорта радионуклидов в нем на популяционном уровне в определенном смысле избыточна: решать задачу санитарно-гигиенической охраны водоема можно, укрупнив структуру модели до уровня, определяющего передачу радионукли­дов из водоема человеку. Естественным образом ре­дуцирование популяционной модели можно сделать, если представить ее подсистемы на уровне гильдий, т. е. совокупности видов, близких в функциональном отношении. Еще проще эта же задача (но, может быть, не в полном объеме) решается на уровне трехкамерной модели, в которой биологическая составляющая из-за сравнительной непродол­жительности своего существования рассматривается как транзитное звено модели.

Структурная схема модели, построенной на уровне гильдий, показана на рис. 2.

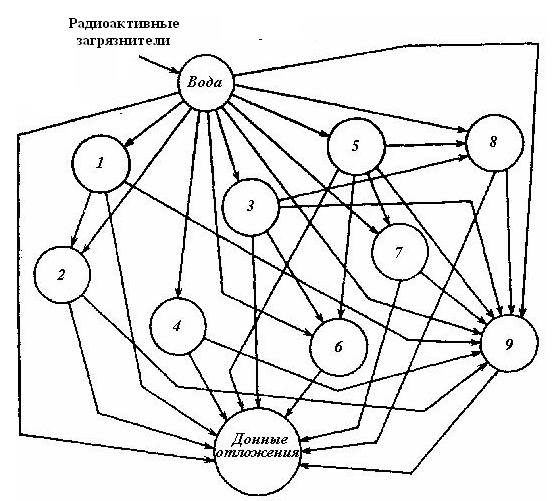
Рис. 2. Структурная схема модели миграции радиоактивного загрязнителя в экосистеме водоема (на гильдиевом уровне): 1 — фитопланктон; 2 — зоопланктон; 3 — микрозообентос; 4 — макрофиты; 5 — моллюски; 6 — ракообразные; 7 — взвеси; 8 — земноводные; 9 — рыбы

Балансовые соотношения для описания динамики накоп­ления радионуклидов в блоках этой модели в общем случае записываются в виде

,

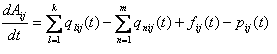где A_ij(t) — накопленная ко времени t активность j-го радионуклида в i-м компоненте экосистемы водоема (в i-м блоке модели); q_lij(t) и q_nij(t) - обменные потоки активности j-го радионуклида между 1-м и i-м и между i-м и n-м компонентами экосистемы (бло­ками модели); f_ij(t) — внешние поступления j-го радионуклида в i-й компонент; р_ij(t) — безвозвратные потери (стоки) j-го радионукли­да из i-го блока (компонента экосистемы); k — число компонентов, "вносящих" j-й радионуклид в i-й компонент; m - число компонен­тов экосистемы, в которые "вносятся" радионуклиды из i-го компонента.

Дополненная начальными условиями система уравнений опишет динамику радионуклидов в каждом из блоков структурной схемы, показанной на рис. 3, и может послужить для прогноза радиационного состояния водоема, его экосистемы при дли­тельном воздействии радионуклидов.

Привлекая далее связи, определяющие радиационное воздействие водоема (его компонентов) на человека, модель позволит оценить дозу этого воздействия. Однако использовать данную модель сегодня для прогноза или описания динамики радиоактивного загряз­нителя в водоеме, к сожалению, нельзя: недостает необходимой ин­формации. Анализ и определение структуры отдельных компонентов указанного выше уравнения, определение числовых значений параметров может являться  одной из основных задач исследований, проводимых на водоеме в рамках радиационного экологического мониторинга.

При наличии экспериментальных данных о поведении радио­нуклидов в водоемах позволяют реа­лизовать модель, удовлетворяющую требованиям санитарно-гигиенического принципа защиты человека от радиационных воздействий, и использовать ее как для оценок радиационных воздействий, так и нормирования радиоактивных по­ступлений в водоем. Для этого общую схему мигра­ции радионуклидов в компонентах водоема (рис. 2) следует редуцировать, но так, чтобы, с одной стороны, сохранить те компоненты водоема, которые участвуют в формировании дозовой нагрузки на человека, а с другой стороны, не оставить те из компо­нентов, конкретная (количественная) роль которых в переносе радионуклидов пока не определена.

С учетом этих условий следует выбрать для модели следующие ком­поненты экосистемы водоема:

-                   вода водоема (компонент экосистемы, в который поступает радиоактивный загрязнитель, он же обеспечивает сток радиоактивного загрязнителя из водоема за счет контакта со сторонними водными системами; компонент, передающий радионуклиды другим компонентам экосистемы водоема и непосредственно участвующий в формировании дозовой нагрузки на человека);

-                   гидробионты (компонент экосистемы, активно участвующий в круговороте веществ, обеспечивающий биологическую дезактивацию воды водоема и непосредственно участвующий в формировании дозовой нагрузки на человека);

-                   донные отложения (место накопления радиоактивного загрязнителя).

Таким образом, упрощение общей схемы модели до трехблочной «вода — гидробионты — донные отложения» является результатом системного подхода к рассматриваемой задаче, основанного на общих закономерностях переноса и накопления радиоактивного загрязнителя в водоеме. Все это основывается на следующих результатах анализа конкретных характеристик, присущих водоемам:

1. Процесс перераспределения поступивших в воду водоема радионуклидов по абиотическим и биотическим компонентам экосистемы и связь их с внешними объектами определяются действующими гид­рологическими и биохимическими факторами.

2.      В любой момент времени активность радионуклидов в биоло­гических компонентах водоема меньше, чем в аби­отических.

3.      Активность радионуклидов в биотических компонентах одно­значно связана с активностью радионуклидов в абиотических компо­нентах, причем абиотический компонент "донные отложения" - глав­ный хранитель радиоактивного загрязнителя в водоеме.

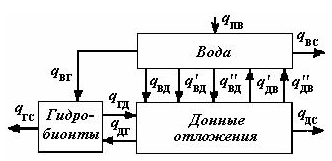
Рис. 3. Структурная схема редуци­рованной модели миграции радиоактив­ного загрязнения в водоеме

Учитывая упрощение общей схемы миграциии загрязнителя в водоеме, приходим к схеме мигра­ции, показанной на рис. 3: В - вода водоема (водный ре­зервуар радионуклидов); Г - гидробионты (биотический резервуар); Д — донные отложения (донный резервуар); q — потоки радиоактив­ного загрязнителя в трехблочной системе В—Г—Д: q_ПВ — внешние по­ступления радиоактивного загрязнителя в воду водоема (источники); q_ВС, q_ГС, q_ДС — необратимые потери загрязнителя (сто­ки) из водного, биотического и донного резервуаров; q_ГВ - потребление загрязнителя гидробионтами из водного резервуара; q_ГД - поступление загрязнителя из биотического резервуара в донный за счет отмирания гидробионтов и их выделений; q_ДГ — потребление загряз­нителя гидробионтами из донного резервуара; q^*_ВД - поступление ра­диоактивного загрязнителя из водного резервуара в донный за счет осаждения минеральных взвесей и при фильтрации; q’_ВД   - то же за счет сорбции растворенной части загрязнителя донными отложения­ми; q’_ДВ   — процесс, обратный предыдущему; q”_ВД - осаждение взму­ченных донных отложений обратно на дно; q”_ДВ — обратный преды­дущему процесс.

Система уравнений, соответствующая принятой схеме модели миг­рации радиоактивного загрязнителя в водоеме, имеет вид (для упрощения записана для одного j-го радионуклида):

,

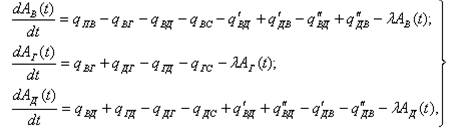где A_В(t), A_Г(t), A_Д(t) - активность радиоактивного загрязнителя (j-го радионуклида) в воде, гидробионтах и донных отложениях со­ответственно; λ — постоянная распада j-го радионуклида.

Для параметризации данной модели и отыскания путей ее решения воспользуемся рядом других характеристик, не упомя­нутых выше. Водоем можно рассматривать как систему с идеальным перемешиванием, так что A_В(t) = c_В(t)M_В, где c_В(t) — удельная активность j-го радионуклида в воде; M_В - масса воды во­доема (или объем). Накопленную ко времени t активность радионуклида j в биотическом резервуаре определим по средней удель­ной активности c_Г(t) в составляющих гидроценоза водоема, каждая из которых имеет удельную активность c_Гi(t) и массу М_Гi(t), так что

,

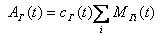причем

.

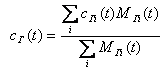Следовательно q_ВГ = aA_В(t)M_Г(t), а q_ВГ =βA_Д(t)M_Г(t), где а и β - коэффициенты пропорциональности. Поток q_ВД  равен

,

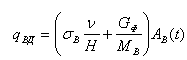где ν — средняя гранулометрическая крупность взвесей; σ — доля А_В(t) на взвесях в воде водоема; G_Ф — расход воды на фильтрацию в дно водоема; H - глубина водоема. Понятно, что q_ГВ = κA_Г(t), где κ — коэффициент, характеризующий скорость поступления j-го радионук­лида из резервуара "гидробионты" на дно водоема: потоки q_ВС, q_ДС и q_ГС (потоки стока из компонентов водоема) можно представить в следующем виде: q_ВС =(G_ст + ξ_впG_исп) c_В(t), q_ДС = G_Фξ_вдc_В(t), q_СГ = χA_Г(t), причем G_ст - расход воды водоема на поверхностный сток; G_исп - расход воды на испарение; ξ_вп, ξ_вд - коэффициенты распределения активности в системах вода-пар и вода-фильтрат; χ — коэффициент, учитывающий унос активности гидробионтов поверхностным стоком из водоема. Принимая эти положения, можем заключить, что представленная систе­ма становится решаемой, поскольку есть возможность определить все ее параметры.

Дальнейшее упрощение рассматриваемой модели можно видеть в выделении достаточно большого временного интервала моделирования, например, 1 год. Тогда М_Г(t) = М_Г, т.е. средней массе гидробионтов в водоеме в течение года (не меняется от года к году), а активность j-го радионуклида из блока «вода» в блок «донные отложе­ния" переносятся блоком «гидробионты» транзитом, поскольку время жизни основной массы гидробионтов меньше года, а процесс аккумуляции ими радиоактивного загрязнителя заканчивается за время от нескольких минут до нескольких суток, для отдельных видов — нескольких недель. При таком временном масштабе моделирования естественно считать, что q’_ВД = q’_ДВ и q”_ВД = q”_ДВ. Поэтому в расчете на год данная система упрощается и принимает вид:

,

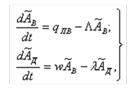где Λ — параметр самоочищения воды водоема от j-го радионуклида - определяет скорость самоочищения воды; w -параметр, определяющий скорость накопления j-го радионуклида в донных отложениях водоема (Λ и w - системные эмпирические характеристики водоема, учитывающие в явной и неявной форме все его особенности и особенности его гидроценоза, т. е. гидрохимический, гидробиологический и гидрологический режимы экосистемы водоема).

В явном виде изменения во времени удельной активности j-го радионуклида в воде водоема c_В(t) и в донных отложениях c_Д(t) определяются соотношениями

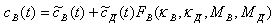
и

,

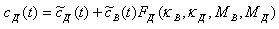в которых 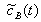 и 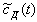 — значения удельной активности j-го радио­нуклида в воде и донных отложениях, накопленной ко времени на­чала наблюдений; F_В и F_Д — функции, определяющие взаимодейст­вие донных отложений с водной массой водоема, они за­висят от значений коэффициента перехода радионуклидов из донных отложений в воду при взмучивании турбулентными пульсациями в водной массе (κ_В), значений коэффициента распределения j-го ради­онуклида в системе взвесь-вода (κ_Д) и масс донных отложений (М_Д) и воды (М_В).

Чтобы воспользоваться последними вышеуказанными соотношениями для определения удельной активности радиоактивного загрязнителя (j-го радио­нуклида) в воде и донных отложениях, установить динамику актив­ности j-го радионуклида, надо знать ряд параметров. Большинство этих параметров извест­но или рассчитывается известными методами, другие следует опреде­лять из временных рядов наблюдений на водоеме. К числу последних относится параметр самоочищения воды водоема, его обы­чно определяют из результатов наблюдений за поведением радиоактив­ного загрязнителя в конкретном водоеме.

Параметр самоочищения воды водоема от радиоактивного загрязнителя (j-го радионуклида) определяют по данным об удельной активности этого радионуклида в воде и донных отложениях с учетом того экспериментального факта, что процесс самоочищения воды про­исходит со скоростью, существенно большей скорости радиоактивно­го распада нуклида. Ниже представлено соотноше­ние для расчета Λ по экспериментальной информации о c_Д(t) и c_В(t):

,

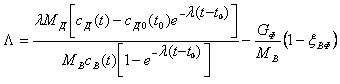где t₀ — время начала измерений c_Д и c_В на водоеме.

Рас­считав по этой формуле и экспериментальным данным значения Λ для водоема, можно получить параметры самоочищения воды водоема относительно всех радионуклидов. Время полуочищения воды водоемов от всех радионуклидов (⁵⁴Mn, ⁶⁰Со, ¹³⁴Cs, ¹³⁷Cs, а также ¹⁴⁴Ce, ¹⁰⁶Ru, ⁹⁰V) чаще всего составляет несколько суток, а это же время для ⁹⁰Sr — год или даже годы. Это есть следствие того факта, что ⁹⁰Sr в воде обычно находится в растворенном виде, слабо аккумулиру­ется гидробионтами и потому не выводится в течение длительного вре­мени в донные отложения. Другие радионуклиды интенсивно аккуму­лируются гидробионтами, взвесями и в сравнительно короткое время выводятся из воды.

Разброс значений Λ и соответственно времени полусамоочищения воды водоема связан впрямую с разбросом экспериментальных данных об удельной активности нуклида в воде и донных отложениях, обусловленном малыми значениями активности, но в то же время реально отражает процессы, происходящие в водоеме.

Список литературы:

1.     Оценка влияния радиационного загрязнения на здоровье человека. -- Новосибирск: АртИнфоДата, 2006

2.     Домбровский Ю.А., Ильичев В.Г., Селютин В.В., Сурков Ф.А. Теоретические и прикладные аспекты моделирования первичной продукции водоемов. Ростов на Дону: Изд-во Ростовского ун-та. 1990. – 176 с