Оглавление
Модели информационного канал с помехами. 2
Двойной симметричный канал. 2
Емкость канал связи. 3
Обнаружение и исправление ошибок при передаче через канал с помехами. 4
Способы борьбы с ошибками. 4
Совершенные коды Хэмминга и Голея. 4
Групповые коды.. 6
Блочные коды.. 6
Квазисовершенные коды БЧХ.. 7
Совершенные и квазисовершенные коды.. 8
Табличное, матричное и полиноминальное кодирование. 8
Матричное кодирование. 9
Полиноминальное кодирование. 9
Максимальные скорости передачи по каналу с помехами. 10
Примеры кодов обнаружения и исправления. 10
Общие свойства помехозащищенного кодирования. 13
Модели информационного канал с помехами
Обработка информации в вычислительных системах невозможна без передачи сообщений между отдельными элементами (оперативной памятью и процессором, процессором и внешними устройствами). Примеры процессов передачи данных приведены в следующей таблице.
|
Передатчик |
Канал |
Приемник |
|
|
Разговор людей |
Голосовой аппарат человека |
Воздушная среда. Акустические колебания |
Слуховой аппарат человека |
|
Телефонный разговор |
Микрофон |
Проводник. Переменный электрический ток |
Динамик |
|
Передача данных в сети Интернет |
Модулятор |
Проводник. Оптоволоконный кабель. Переменный электрический ток. Оптический сигнал |
Демодулятор |
|
Радиотелефон, рация |
Радиопередатчик |
Эфир. Электромагнитные волны |
Радиоприемник |
В перечисленных выше процессах передачи можно усмотреть определенное сходство. Общая схема передачи информации, показана на рис. 1.
В канале сигнал подвергается различным воздействиям, которые мешают процессу передачи. Воздействия могут быть непреднамеренными (вызванными естественными причинами) или специально организованными (созданными) с какой-то целью некоторым противником. Непреднамеренными воздействиями на процесс передачи (помехами) могут являться уличный шум, электрические разряды (в т. ч. молнии), магнитные возмущения (магнитные бури), туманы, взвеси (для оптических линий связи) и т.п.
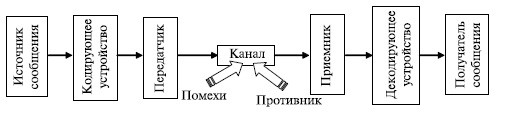
Рис. 1. Общая схема передачи информации
Для изучения механизма воздействия помех на процесс передачи данных и способов защиты от них необходима некоторая модель. Процесс возникновения ошибок описывает модель под названием двоичный симметричный канал (ДСК), схема которой показана на рис. 2 .
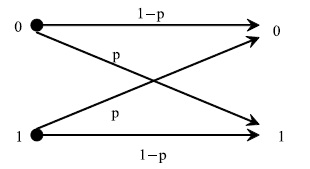
Рис. 2. Схема двоичного симметричного канала
При
передаче сообщения по ДСК в каждом бите
сообщения с вероятностью 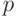 может
произойти ошибка, независимо от наличия ошибок в других битах. Ошибка
заключается в замене знака 0 на 1 или 1 на 0.
может
произойти ошибка, независимо от наличия ошибок в других битах. Ошибка
заключается в замене знака 0 на 1 или 1 на 0.
Некоторые типы ошибок:
·
замена знака 0 на 1 или 1 на 0 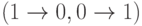 ;
;
·
вставка знака 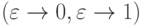 ;
;
·
пропуск знака 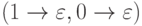 .
.
Чаще других встречается замена знака. Этот тип ошибок исследован наиболее полно.
Емкость канал связи
Используют следующие характеристики канала
·
Эффективно передаваемая полоса частот 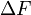 ;
;
·
Динамический диапазон 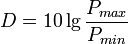 ;
;
· Волновое сопротивление;
· Пропускная способность;
·
Помехозащищённость 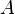 ;
;
·
Объём 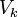 .
.
Помехозащищённость 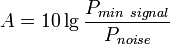 . Где
. Где 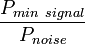 — минимальное отношение сигнал/шум;
— минимальное отношение сигнал/шум;
Объём канала 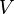 определяется по формуле:
определяется по формуле: 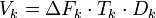 ,
,
где 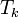 —
время, в течение которого канал занят передаваемым сигналом;
—
время, в течение которого канал занят передаваемым сигналом;
Для передачи сигнала по каналу без искажений объём канала 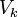 должен
быть больше либо равен объёму сигнала
должен
быть больше либо равен объёму сигнала 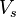 , то есть
, то есть 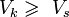 . Простейший случай вписывания объёма
сигнала в объём канала — это достижение выполнения неравенств
. Простейший случай вписывания объёма
сигнала в объём канала — это достижение выполнения неравенств 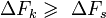 ,
, 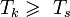 > и
> и 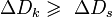 . Тем не менее,
. Тем не менее, 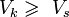 может выполняться и в других случаях, что
даёт возможность добиться требуемых характеристик канала изменением других
параметров. Например, с уменьшением диапазона частот можно увеличить полосу
пропускания.
может выполняться и в других случаях, что
даёт возможность добиться требуемых характеристик канала изменением других
параметров. Например, с уменьшением диапазона частот можно увеличить полосу
пропускания.
Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.
Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях сетевой модели OSI).
В системах связи возможны несколько стратегий борьбы с ошибками:
· обнаружение ошибок в блоках данных и автоматический запрос повторной передачи повреждённых блоков — этот подход применяется, в основном, на канальном и транспортном уровнях;
· обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
· исправление ошибок (англ.forward error correction) применяется на физическом уровне.
На рисунке показано, каким образом реализуются обнаружение и исправление ошибок. Перед записью М-разрядных данных в память производится их обработка, обозначенная на схеме функцией ≪f≫, в результате которой формируется добавочный К-разрядный код. В память заносятся как данные, так и данный вычисленный код, то есть (М + К)-разрядная информация. При чтении информации повторно формируется К-разрядный код, который сравнивается с аналогичным кодом, считанным из ячейки. Сравнение приводит к одному из трех результатов:
1) Нe обнаружено ни одной ошибки. Извлеченные из ячейки данные подаются на выход памяти.
2) Обнаружена ошибка, и она может быть исправлена. Биты данных и добавочного кода подаются на схему коррекции. После исправления ошибки в М-разрядных данных они поступают на выход памяти.
3) Обнаружена ошибка, и она не может быть исправлена. Выдается сообщение о неисправимой ошибке.
Совершенные коды Хэмминга и Голея|
В этом подразделе мы подробнее опишем три типа линейных блоковых кодов, которые часто встречаются на практике и характеризуются своими важными параметрами. Коды Хемминга. Сюда относятся как двоичные, так и недвоичные коды Хемминга. Мы ограничим обсуждение свойствами двоичных кодов Хемминга. Они включают класс кодов со свойствами
где Если необходимо генерировать систематический код Хемминга, то
проверочная матрица Заметим, что любые два столбца матрицы Путём прибавления ко всем кодовым комбинациям
где Код Голея. Двоичный код Голея — один из двух связанных друг с другом исправляющих ошибки линейных кодов: ·
совершенный
двоичный код Голея
— совершенный двоичный код
с параметрами · расширенный двоичный код Голея ,получающийся из совершенного добавлением бита контроля чётности и имеющий параметры [24,12,8]. Код Голея – это двоичный линейный код Таблица 8.1.1. Распределение весов кода Голея
|
Множество всех двоичных слов 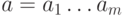 длины
длины 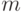 образует абелеву (коммутативную) группу относительно
поразрядного сложения.
образует абелеву (коммутативную) группу относительно
поразрядного сложения.
Пусть 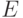 -
кодирующая
-
кодирующая  -матрица,
у которой есть
-матрица,
у которой есть 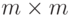 -подматрица
с отличным от нуля определителем, например, единичная. Тогда отображение
-подматрица
с отличным от нуля определителем, например, единичная. Тогда отображение 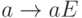 переводит группу всех двоичных слов
длины
переводит группу всех двоичных слов
длины 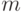 в
группу кодовых слов длины
в
группу кодовых слов длины 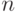 .
.
Предположим, что 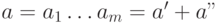 . Тогда для
. Тогда для 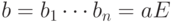 ,
, 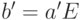 ,
, 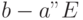 ,
получаем
,
получаем
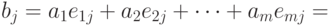

т.е. 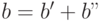 . Следовательно, взаимно-однозначное отображение группы
двоичных слов длины
. Следовательно, взаимно-однозначное отображение группы
двоичных слов длины 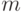 при помощи заданной матрицы
при помощи заданной матрицы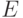 сохраняет свойства групповой операции,
что означает, что кодовые слова образуют группу.
сохраняет свойства групповой операции,
что означает, что кодовые слова образуют группу.
Блочный код называется групповым, если его кодовые слова образуют группу.
Если код является групповым, то наименьшее расстояние между двумя кодовыми словами равно наименьшему весу ненулевого слова.
Это следует из соотношения  .
.
В предыдущем примере наименьший вес ненулевого слова равен 3. Следовательно, этот код способен исправлять однократную ошибку или обнаруживать однократную и двойную.
При использовании группового кода незамеченными остаются те и только те ошибки, которые отвечают строкам ошибок, в точности равным кодовым словам.
Такие строки ошибок переводят одно кодовое слово в другое.
Следовательно, вероятность того, что ошибка останется необнаруженной, равна сумме вероятностей всех строк ошибок, равных кодовым словам.
Блочные кодыПусть кодируемая информация делится на фрагменты длиной k бит, которые преобразуются в кодовыеслова длиной n бит. Тогда соответствующий блоковый код обычно обозначают 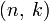 . При этом число
. При этом число 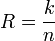 называется скоростью кода.
называется скоростью кода.
Если исходные k бит код оставляет неизменными, и добавляет n − k проверочных, такой код называетсясистематическим, иначе несистематическим.
Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из kинформационных бит сопоставляется n бит кодового слова. Однако, хороший код должен удовлетворять, какминимум, следующим критериям:
· способность исправлять как можно большее число ошибок,
· как можно меньшая избыточность,
· простота кодирования и декодирования.
Нетрудно видеть, что приведённые требования противоречат друг другу. Именно поэтому существуетбольшое количество кодов, каждый из которых пригоден для своего круга задач.
Практически все используемые коды являются линейными. Это связано с тем, что нелинейные кодызначительно сложнее исследовать, и для них трудно обеспечить приемлемую лёгкость кодирования идекодирования.
Линейными называются коды, в которых проверочные символы представляют собой линейные комбинации информационных символов.
Для двоичных кодов в качестве линейной операции используют сложение по модулю 2.
Правила сложения по модулю 2 определяются следующими равенствами:
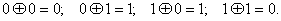
Последовательность нулей и единиц, принадлежащих данному коду, будем называть кодовым вектором.
Свойство линейных кодов: сумма (разность) кодовых векторов линейного кода дает вектор, принадлежащий данному коду.
Линейные коды образуют алгебраическую группу по отношению к операции сложения по модулю 2. В этом смысле они являются групповыми кодами.
Свойство группового кода: минимальное кодовое расстояние между кодовыми векторами группового кода равно минимальному весу ненулевых кодовых векторов.
Вес кодового вектора (кодовой комбинации) равен числу его ненулевых компонентов.
Расстояние между двумя кодовыми векторами равно весу вектора, полученного в результате сложения исходных векторов по модулю 2. Таким образом, для данного группового кода
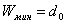 .
.
Групповые коды удобно задавать матрицами,
размерность которых определяется параметрами кода 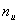 и
и 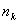 .Число
строк матрицы равно
.Число
строк матрицы равно 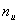 , число столбцов
равно
, число столбцов
равно 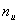 +
+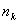 =
=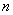 :
:
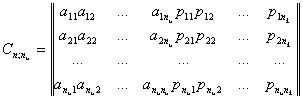
Коды, порождаемые
этими матрицами, известны как 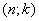 -коды,
где
-коды,
где 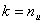 , а
соответствующие им матрицы называют порождающими, производящими,
образующими.
, а
соответствующие им матрицы называют порождающими, производящими,
образующими.
Порождающая матрица
С может быть представлена двумя матрицами И и П (информационной и
проверочной). Число столбцов матрицы П равно 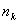 , число
столбцов матрицы И равно
, число
столбцов матрицы И равно 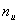 :
:
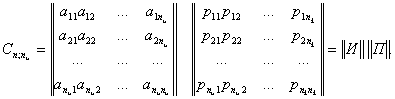
Остался открытым вопрос о методике построения кодов, минимальное расстояние между кодовыми словами которых равно заданному числу. В 1960 году независимо Боуз (Bose), Чоудхури (Chaudhuri) и Хоккенгем (Hocquengem) открыли способ построения полиномиальных кодов, удовлетворяющих таким требованиям. Эти коды получили названия кодов Боуза-Чоудхури-Хоккенгема или БЧХ-кодов (BCH codes). БЧХ-коды могут быть не только двоичными, например, на практике достаточно широко используются недвоичные коды Рида-Соломона (Reed, Solomon), но далее будут рассматриваться только двоичные.
Многочлен 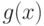 степени
степени 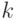 называется примитивным, если
называется примитивным, если 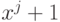 делится
на
делится
на 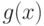 без
остатка для
без
остатка для 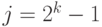 и
не делится ни для какого меньшего значения
и
не делится ни для какого меньшего значения 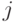 .
.
Например, многочлен 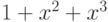 примитивен:
он делит
примитивен:
он делит 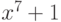 , но
не делит
, но
не делит 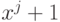 при
при  .
Примитивен такжемногочлен
.
Примитивен такжемногочлен 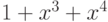 - он делит
- он делит 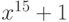 , но не делит
, но не делит 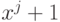 при
при 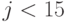 .
.
Кодирующий многочлен 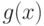 для БЧХ-кода, длина кодовых слов
которого
для БЧХ-кода, длина кодовых слов
которого 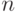 ,
строится так. Находится примитивный многочленминимальной
степени
,
строится так. Находится примитивный многочленминимальной
степени 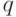 такой,
что
такой,
что 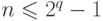 или
или 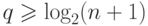 . Пусть
. Пусть  - корень этого многочлена, тогда рассмотрим
кодирующий многочлен
- корень этого многочлена, тогда рассмотрим
кодирующий многочлен 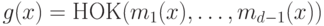 , где
, где 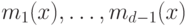 - многочлены минимальной
степени, имеющие корнями соответственно
- многочлены минимальной
степени, имеющие корнями соответственно 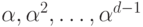 .
.
Построенный кодирующий многочлен производит
код с минимальным расстоянием между кодовыми словами, не меньшим 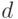 , и
длиной кодовых слов n [1].
, и
длиной кодовых слов n [1].
Пример. Нужно построить БЧХ-код с длиной кодовых слов 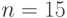 и
минимальным расстоянием между кодовыми словами
и
минимальным расстоянием между кодовыми словами  . Степень примитивного многочлена равна
. Степень примитивного многочлена равна 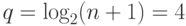 и сам он равен
и сам он равен 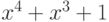 .
Пусть
.
Пусть  -
его корень, тогда
-
его корень, тогда 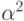 и
и 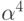 -
также его корни. Минимальным многочленом для
-
также его корни. Минимальным многочленом для 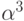 будет
будет 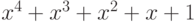 . Следовательно,
. Следовательно,
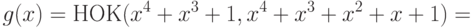
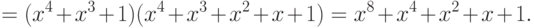
Степень полученного многочлена равна 8, следовательно,
построенный БЧХ-код будет 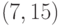 -кодом. Слово 1000100
или
-кодом. Слово 1000100
или 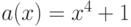 будет закодировано кодовым словом
будет закодировано кодовым словом 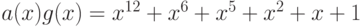 или
111001100000100.
или
111001100000100.
Можно построить1 двоичный БЧХ-код с кодовыми
словами длины 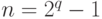 и
нечетным минимальным расстоянием
и
нечетным минимальным расстоянием 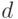 , у которого число контрольных символов не больше
, у которого число контрольных символов не больше 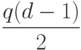 .
.
Первый БЧХ-код, примененный на практике, был 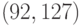 -кодом,
исправляющим ошибки кратности до 5, но наиболее широкое распространение
получил
-кодом,
исправляющим ошибки кратности до 5, но наиболее широкое распространение
получил 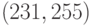 -код,
обнаруживающий ошибки кратности до 6.
-код,
обнаруживающий ошибки кратности до 6.
БЧХ-коды умеренной длины не слишком далеки от совершенных или квазисовершенных кодов. Коды Хэмминга, например, являются БЧХ-кодами, а БЧХ-коды с минимальным весом кодового слова 5 - квазисовершенны. Но с ростом длины кодовых слов качество БЧХ-кодов падает. Код Голея, например, - это не код БЧХ.
код Рида — Соломона.
Пусть 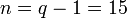 и
и 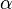 —
примитивный элемент
—
примитивный элемент 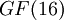 .
Тогда
.
Тогда
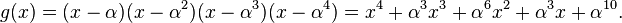
Каждый элемент поля 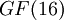 можно сопоставить 4 битам,
поэтому одно кодовое слово эквивалентно 60 = 15 × 4
битам, таким образом набору из 44 бит ставится в соответствие набор из 60 бит.
Можно сказать, что такой код работает с полубайтами
информации.
можно сопоставить 4 битам,
поэтому одно кодовое слово эквивалентно 60 = 15 × 4
битам, таким образом набору из 44 бит ставится в соответствие набор из 60 бит.
Можно сказать, что такой код работает с полубайтами
информации.
Групповой 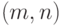 -код,
исправляющий все ошибки веса, не большего
-код,
исправляющий все ошибки веса, не большего 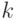 , и никаких других, называется совершенным.
, и никаких других, называется совершенным.
Свойства совершенного кода2:
1.
Для совершенного 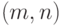 -кода, исправляющего все ошибки веса, не
большего
-кода, исправляющего все ошибки веса, не
большего 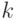 ,
выполняется соотношение
,
выполняется соотношение 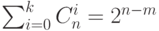 . Верно и обратное утверждение;
. Верно и обратное утверждение;
2.
Совершенный код, исправляющий все ошибки веса, не большего 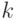 , в
столбцах таблицы декодирования содержит
все слова, отстоящие от кодовых на расстоянии, не большем
, в
столбцах таблицы декодирования содержит
все слова, отстоящие от кодовых на расстоянии, не большем 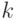 . Верно и
обратное утверждение;
. Верно и
обратное утверждение;
3.
Таблица декодирования совершенного кода,
исправляющего все ошибки в не более чем 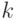 позициях, имеет в качестве лидеров все строки,
содержащие не более
позициях, имеет в качестве лидеров все строки,
содержащие не более 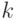 единиц.
Верно и обратное утверждение.
единиц.
Верно и обратное утверждение.
Совершенный код - это лучший код, обеспечивающий максимум минимального расстояния между кодовыми
словами при минимуме длины кодовых слов. Совершенный код легко декодировать:
каждому полученному слову однозначно ставится в соответствие ближайшее кодовое.
Чисел 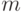 ,
, 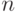 и
и 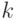
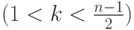 , удовлетворяющих условию совершенности
кода очень мало. Но и при подобранных
, удовлетворяющих условию совершенности
кода очень мало. Но и при подобранных 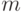 ,
, 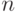 и
и 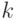 совершенный
код можно построить только в исключительных случаях.
совершенный
код можно построить только в исключительных случаях.
Если 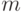 ,
, 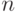 и
и 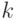 не
удовлетворяют условию совершенности, то лучший групповой код, который им
соответствует называетсяквазисовершенным, если он исправляет все ошибки
кратности, не большей
не
удовлетворяют условию совершенности, то лучший групповой код, который им
соответствует называетсяквазисовершенным, если он исправляет все ошибки
кратности, не большей 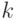 , и
некоторые ошибки кратности
, и
некоторые ошибки кратности  .
Квазисовершенных кодов также очень мало.
.
Квазисовершенных кодов также очень мало.
Табличное кодирование
Схемы табличного кодирования информации не встречаются в живой природе — это изобретение общества. В их основе лежат предварительно созданные таблицы образцов сигналов. Кодируемый сигнал сравнивается с образцами таблицы, из них выбирается ближайший похожий, и записывается не сам сигнал, а его образец.
Поскольку при кодировании элемент информации заменяется элементом данных, теоретически всё равно, какую природу имеет этот элемент — он может быть рисунком, символом, комбинацией знаков. Он также может быть записан и комбинацией цифр. Например, мы можем построить таблицу, в которой каждой букве будет соответствовать её порядковый номер в алфавите. Это пример таблично-цифровой схемы кодирования. Подобные схемы очень удобны, когда речь идёт о кодировании информационных объектов, относящихся не к природе, а к обществу, например для кодирования текстов документов и сообщений.
Важно обратить внимание на то, что хотя при таблично-цифровом кодировании элементы информации и записываются группами цифр, у полученных групп нет числовой природы - - их природа остаётся символьной. Чтобы подчеркнуть, что результатом таблично-цифрового кодирования являются не числа, а группы цифр, этот вид кодирования называют цифровым кодированием.
Матричное кодированиеРанее каждая схема кодирования описывалась
таблицами, задающими кодовое слово длины 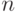 для каждого
исходного слова длины
для каждого
исходного слова длины 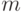 . Для
блоков большой длины этот способ требует большого объема памяти и поэтому
непрактичен. Например, для
. Для
блоков большой длины этот способ требует большого объема памяти и поэтому
непрактичен. Например, для 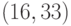 -кода потребуется
-кода потребуется 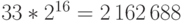 бит.
бит.
Гораздо меньшего объема памяти требует матричное кодирование. Пусть 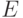 матрица размерности
матрица размерности  , состоящая из элементов
, состоящая из элементов 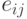 , где
, где 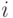 - это номер строки, а
- это номер строки, а 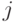 - номер
столбца. Каждый из элементов матрицы
- номер
столбца. Каждый из элементов матрицы 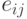 может быть либо 0, либо 1. Кодирование реализуется операцией
может быть либо 0, либо 1. Кодирование реализуется операцией 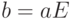 или
или  , где кодовые слова
рассматриваются как векторы, т.е как матрицы-строки размера
, где кодовые слова
рассматриваются как векторы, т.е как матрицы-строки размера  .
.
Пример. Рассмотрим следующую  -матрицу:
-матрицу:
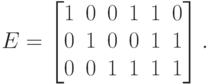
Тогда кодирование задается такими отображениями: 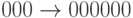 ,
, 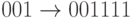 ,
, 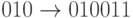 ,
, 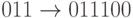 ,
, 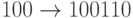 ,
, 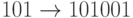 ,
, 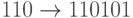 ,
, 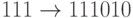 .
.
Рассмотренный пример показывает
преимущества матричного кодирования: достаточно запомнить 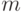 кодовых слов
вместо
кодовых слов
вместо 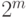 слов. Это
общий факт.
слов. Это
общий факт.
При полиномиальном кодировании каждое сообщение отождествляется с многочленом, а само кодирование состоит в умножении на фиксированный многочлен. Полиномиальные коды - блочные и отличаются от рассмотренных ранее только алгоритмами кодирования и декодирования.
Пусть 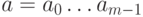 -
двоичное сообщение. Тогда сопоставим ему многочлен
-
двоичное сообщение. Тогда сопоставим ему многочлен  . Все вычисления происходят
в поле классов
вычетов по модулю
2, т. е. от результата любой арифметической операции берется остаток от
его деления на 2.
. Все вычисления происходят
в поле классов
вычетов по модулю
2, т. е. от результата любой арифметической операции берется остаток от
его деления на 2.
Например, последовательности 10011 при  соответствует многочлен
соответствует многочлен 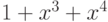 .
.
Зафиксируем некоторый многочлен степени 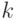 ,
,
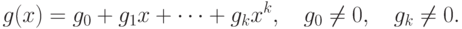
Полиномиальный код с кодирующим многочленом 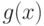 кодирует слово сообщения
кодирует слово сообщения 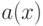 многочленом
многочленом 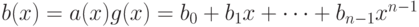 или кодовым словом из коэффициентов этого
многочлена
или кодовым словом из коэффициентов этого
многочлена 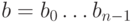 . Условия
. Условия 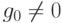 и
и 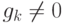 необходимы, потому что в противном случае
необходимы, потому что в противном случае 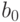 и
и 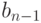 не будут нести никакой информации, т.к. они
всегда будут нулями.
не будут нести никакой информации, т.к. они
всегда будут нулями.
Одной из основных характеристик любой системы передачи информации, кроме перечисленных выше, является ее пропускная способность. Пропускная способность – максимально возможное количество полезной информации, передаваемое в единицу времени:
c = max{Imax} / TC ,
c = [бит/с].
Иногда скорость передачи информации определяют как максимальное количество полезной информации в одно элементарном сигнале:
s = max{Imax} / n,,
s = [бит/элемент].
Рассмотренные характеристики зависят только от канала связи и его характеристик и не зависят от источника.
Примеры кодов обнаружения и исправления.Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.
Для
обнаружения ошибок используют коды обнаружения ошибок, для
исправления — корректирующие коды (коды, исправляющие
ошибки, коды с коррекцией ошибок, помехоустойчивые коды)
Способы борьбы с ошибками
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях сетевой модели OSI).
Коды с обнаружением ошибок
Код с проверкой на четность. Такой код образуется путем добавления к передаваемой комбинации, состоящей из к информационных символов неизбыточного кода, одного контрольного символа (0 или 1), так чтобы общее число единиц в передаваемой комбинации было четным. Таким образом, общее число символов nв передаваемой комбинации:
n=k+1 В первом столбце приведены примеры
|
k |
m |
n = k+m |
|
11011 10101 00010 11011 11111 |
0 1 1 0 1 |
11011 0 11011 1 00010 1 11101 0 11111 1 |
передачи отдельных комбинаций пятиразрядного двоичного кода на все сочетания (k - символы).
Во втором столбце к этим комбинациям приписывается контрольный символ 1, если сумма единиц в кодовой комбинации нечетная, или 0, если сумма единиц четная. В нашем примере длина исходной кодовой комбинацииk=5 позволяет при таком числе разрядов передать N=25=32 кодовые комбинации. И хотя приписывание контрольного символа и увеличивает разрядность кода до n=6, число передаваемых комбинаций остается прежним. Поэтому общее число комбинаций.
N=2n-1
Таким образом, этот код обладает избыточностью, т.к. в нашем примере вместо N=26=64 комбинаций может быть послано только N=26-1=32 комбинаций.
В кодировании избыточности определяется отношением контрольных символов m к информационным k в одном слове:
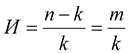 (3-8)
(3-8)
Для пятиразрядного кода с проверкой на четность И=1/5. Очевидно, что чем длиннее кодовая комбинация, тем меньше избыточность и больше экономичность кода. Добавление контрольного символа увеличивает кодовое расстояние в передаваемых комбинациях от d=1 до dmin=2.
На приемной стороне производится так называемая проверка на четность. В принятых комбинациях подсчитывается количество единиц: если оно четное, считается, что искажений не было. Тогда последний контрольный символ отбрасывается и записывается первоначальная комбинация. Очевидно, что четное число искажений такой код обнаружить не может, т.к. число единиц при этом снова будет четным.
В то же время этот код может обнаружить не только одиночные, но и тройные и пятерные ошибки и т.д. ошибки, т.е. любое возможное нечетное число ошибок, т.к. сумма единиц в принятой кодовой комбинации становится нечетной. Однако если велика вероятность появления многократных ошибок, такой код использовать нецелесообразно, т.к. несмотря на то, что можно обнаружить все слова с нечетным количеством ошибок, число кодовых комбинаций с четным числом ошибок окажется велико, и передача будет сопровождаться большими искажениями.
По изложенному принципу строится код с проверкой на нечетность.
Код с постоянным числом единиц и нулей в комбинациях.
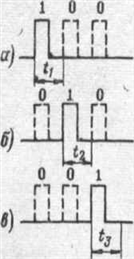
Общее
число кодовых комбинаций в двоичном коде с постоянным весом равно: N=Сln=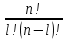 (3-9)
(3-9)
где l - число единиц в слове длиной n.
|
Код c52 |
Код c73 |
|
00011 00101 01010 11000 |
1010100 0101010 1110000 1001001 |
Наиболее употребляемыми являются пятиразрядный код с двумя единицами (N= c52=10) и саморазрядный код с тремя единицами (N= с73=35).
Эти коды более помехоустойчивые, чем код с проверкой на четность, т.к. позволяют обнаруживать большее число искажений.
Правильность принятых кодовых комбинаций в кодах определяется путем подсчета количества единиц, и если, например, в коде с c52 принято на две единицы, а в коде c73 не три единицы, то в передаче произошла ошибка. Очевидно, что код c73 может обнаружить все одиночные ошибки, т.к. в этом случае в комбинации будет либо две единицы, либо четыре. Кроме того, этот код позволяет обнаружить часть многократных ошибок (двойные, тройные и т.п.), за исключением случаев, когда одна из единиц переходит в нуль, а один из нулей в единицу (такое двойное искажение называется смещением). При двойных смещениях (переход двух единиц в нуль и двух нулей в единицу) искажение также не обнаруживается.
Все сказанное правомочно и для кода c52.
Распределительный код. Это также разновидность кода на определенное число сочетаний. В данном случае на сочетание cln.. В любой кодовой комбинации длины n содержится только одна единица. Число кодовых комбинаций распределительного кода равно:
N=cln=n (3-10)
Кодовые комбинации при n=6 можно записать: 000001, 000010, 000100, 001000, 010000, 100000.
Сложение по модулю 2 двух комбинаций показывает, что они отличаются друг от друга на кодовое расстояние d=2.
На рисунке показаны 3 кодовые комбинации: 100, 010, 001 для кода n=3. В системах телемеханики этот код нашел широкое применение из-за простой схемной реализации.
Код с числом единиц, кратным трем. Этот код образуется путем добавления к k информационным символам двух дополнительных контрольных символов (m = 2), имеющих такие значения, чтобы сумма единиц посылаемых в линию кодовых комбинаций была кратной трем. Примеры комбинаций такого кода представлены в таблице:
|
k |
m |
n = k+m |
|
000110 100011 101011 |
10 00 11 |
00011010 10001100 10101111 |
Такой код позволяет обнаружить все одиночные ошибки и любое четное количество ошибок одного типа (например, только переход 0 в 1). Не обнаруживаются двойные ошибки различных типов (т.е. смещения) и ошибки одного типа, кратные 3.
На приеме полученная комбинация проверяется на кратность 3. При наличии такой кратности считается, что ошибок не было, два контрольных знака отбрасываются и записывается исходная комбинация.
Код с удвоением элементов (корреляционный код).
Помехоустойчивость кода может быть повышена путем установления определенных зависимостей между элементами кодовых комбинаций. Примером такого кода является корреляционный код, который строится следующим образом.
Каждый элемент двоичного кода на все сочетания передается двумя символами, причем 1 преобразуется в 10, а 0 в 01. Вместо комбинации 1010011 передается 10 01 10 01 01 10 10.
Таким образом, корреляционный код содержит вдвое больше элементов, чем исходный (И = 1). На примере ошибка обнаруживается в том случае, если в парных элементах будут содержаться одинаковые символы, т.е. 11 или 00 (вместо 10 и 01). При правильном приеме вторые (четные) элементы отбрасываются, и остается первоначальная комбинация.
Код обладает высокой помехоустойчивостью, т.к. ошибка не обнаруживается, лишь когда два рядом стоящих различных символа, соответствующих одному элементу исходной кодовой комбинации, будут искажены так, что 1 перейдет в 0, а 0 в 1.
Инверсный код. В таком коде для увеличения помехоустойчивости к исходной n-разрядной комбинации по определенному правилу добавляется еще n - разрядов. В линию посылается удвоенное число символов. Правило образования кода следующее: если в исходной комбинации четное число единиц, то добавляемая комбинация повторяет исходную, если нечетное, то в добавляемых разрядах все 0 превращаются в 1, а 1 в 0 (т.е. комбинация инвертируется по отношению к исходной). Пример:
|
k |
m |
Инверсный код n = k+m |
|
110001 111101 111111 111100 |
1110001 1111101 0000000 0000011 |
11100011110001 11111011111101 11111110000000 11111000000011 |
Разработка методов помехоустойчивого кодирования, была инициирована основанной теоремой Шеннона для дискретного канала с шумом, указывающей на существование практически безошибочного метода передачи информации по такому каналу со скоростью, не превышающей пропускную способность этого канала. Названный метод передачи информации предполагает использование корректирующего кода, основанного на введении специально организованной избыточности.
Корректирующие коды подразделяются на блочные и непрерывные. В блочныхкодах каждому передаваемому сообщению (кодовому вектору, состоящему из m символов) сопоставляется блок из n символов (n > m). В непрерывных (рекуррентных или цепных) кодахсимволы, не подразделяются на блоки и представляют собой непрерывную последовательность. И блочные и непрерывные коды делятся на разделимые, и неразделимые. У разделимых кодов информационные и проверочные символы имеют определенные позиции, неразделимые же коды таким свойством не обладают.
Разделимые блочные коды подразделяются, на линейные и нелинейные. Линейные коды часто называют групповыми кодами, поскольку кодовые вектора этих кодов состоят из элементов поля, состоящего из двух абелевых групп. Важнейшей в практическом плане разновидностью таких кодов являются двоичные групповые коды, алфавит которых состоит из двух символов: "0" и "1", образующих поле с двумя абелевыми группами: группу по двоичному умножению и группу по операции сложения по модулю 2 (именно таким кодам и посвящена настоящая лабораторная работа). Наиболее лаконичной формой записи данных кодов является матричная форма, которая и используется далее.














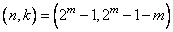 ,
(8.1.16)
,
(8.1.16)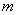 -
некоторое положительное целое число.
Например, если
-
некоторое положительное целое число.
Например, если 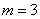 ,
мы имеем код (7, 4). Проверочная матрица
,
мы имеем код (7, 4). Проверочная матрица  кода
Хемминга имеет особое свойство, которое позволяет нам существенно облегчить
описание кода. Напомним, что проверочная матрица
кода
Хемминга имеет особое свойство, которое позволяет нам существенно облегчить
описание кода. Напомним, что проверочная матрица 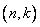 кода
имеет
кода
имеет 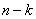 строк
и
строк
и 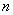 столбцов.
Для двоичного
столбцов.
Для двоичного 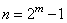 столбцов
состоят из всех возможных двоичных векторов с
столбцов
состоят из всех возможных двоичных векторов с 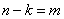 элементами,
исключая вектор со всеми нулевыми элементами. Для
примера, код (7, 4), рассмотренный в примерах 8.1.1 и 8.1.2, является кодом
Хемминга. Его проверочная матрица состоит из семи вектор-столбцов
(001), (010), (011), (100), (101), (110), (111).
элементами,
исключая вектор со всеми нулевыми элементами. Для
примера, код (7, 4), рассмотренный в примерах 8.1.1 и 8.1.2, является кодом
Хемминга. Его проверочная матрица состоит из семи вектор-столбцов
(001), (010), (011), (100), (101), (110), (111).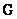 можно
получить из (8.1.11).
можно
получить из (8.1.11).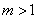 возможно
найти три столбца из
возможно
найти три столбца из 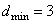 .
.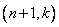 с
с 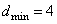 .
С другой стороны,
.
С другой стороны, 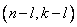 путём
удаления
путём
удаления 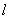 строк порождающей матрицы
строк порождающей матрицы 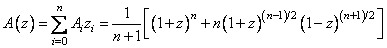 ,
(8.1.17)
,
(8.1.17)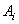 -
число кодовых слов с весом
-
число кодовых слов с весом 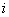 .
.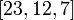 , или
, или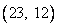 с
с 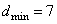 .
Расширенный двоичный линейный код Голея
.
Расширенный двоичный линейный код Голея 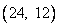 с
с 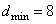 получается
из кода Голея путём добавления ко всем кодовым комбинациям проверочного
символа. Таблица (8.1.1) показывает распределение весов кодовых слов кода
Голея
получается
из кода Голея путём добавления ко всем кодовым комбинациям проверочного
символа. Таблица (8.1.1) показывает распределение весов кодовых слов кода
Голея  (zip - application/zip)
(zip - application/zip)










