Содержание
Вступление
1. Оптимизация решений динамическими методами
2. Динамическая оптимизация в планировании работ
3. Задачи принятия решений в условиях риска
4. Задачи принятия решений в условиях неопределенности
Литература
ВСТУПЛЕНИЕ
Одной из составных частей современной науки управления является набор количественных методов исследования сложных явлений и процессов. В условиях совершенствования систем управления промышленностью и экономикой количественные методы придают процессу управления необходимую научную обоснованность, сводят до минимума элемент субъективности при выборе управленческих решений и позволяют в определенной мере оптимизировать как сам процесс управления, так и комплекс технических средств, обеспечивающих его осуществление.
Принятие решений является основной составляющей управления (основным этапом процессов управления). Поскольку общей наукой об управлении, охватывающей теорию и практику всего комплекса вопросов, связанных с целенаправленным руководством со стороны человека, течением и результатами его деятельности в любой области, связанной с процессами управления, является кибернетика, то естественно теорию принятия решений считают разделом кибернетики.
Процесс теории принятия решений обусловлен быстрым развитием разработок, проектирования, внедрения и использования в различных сферах народного хозяйства автоматизированных систем управления (АСУ). Каждый специалист, в той или иной степени участвующий в управлении сложным объектом, в реальных условиях всегда сталкивается как с элементами математического, программного, информационного и технического обеспечения процесса управления, так и с недостаточностью нужной для управления и принятия решений информации. Использование для управления АСУ требует и будет требовать вес возрастающих объемов информации, так как полнота данных во многом определяет качество машинных решений, вырабатываемых системой.
Принятые решения — понятие, близкое к выбору из множества возможностей. Это понятие базируется не только на количественных характеристиках, но и на факторах, не всегда имеющих количественные меры.
Учет этих факторов необходим также и потому, что в настоящее время четко определилась тенденция применения методов моделирования и оптимизации явлений, позволяющая выполнять формальную сторону подготовки и принятия решения на ЭВМ. Поэтому вопросы: какие составляющие процесса принятия решения должен контролировать человек, принимающий решения, и какие составляющие могут быть выполнены вычислительным комплексом, как осуществить взаимосвязь человека с этим комплексом - стали насущными вопросами теории и практики принятия решений. Без исследования этих вопросов вряд ли могут быть достигнуты какие-либо серьезные успехи в создании и исследовании автоматизированных систем управления.
1. ОПТИМИЗАЦИЯ РЕШЕНИЙ ДИНАМИЧЕСКИМИ МЕТОДАМИ
Задача 1.1
Фирма обеспечивает поставку товаров для продажи с базы А0 в четыре торговые точки А1, А2, А3, А4. Расстояния между всеми пунктами известны и заданы в километрах (Таблица 1).
В целях экономии времени и средств необходимо найти такой маршрут передвижения, при котором, побывав в каждой торговой точке по одному разу, поставщик вернулся бы в исходный пункт А0, проделав минимально возможный суммарный путь.
Таблица 1.1.10 – Исходные данные.
|
А0 |
А1 |
А2 |
А3 |
А4 |
|
|
А0 |
0 | 200 | 150 | 300 | 100 |
|
А1 |
200 | 0 | 120 | 350 | 200 |
|
А2 |
150 | 120 | 0 | 150 | 250 |
|
А3 |
300 | 350 | 150 | 0 | 150 |
|
А4 |
100 | 200 | 250 | 150 | 0 |
Решение
Видно, что матрица симметрична относительно главной диагонали, поэтому достаточно информации одной из ее половин. Расстояния определяются для конкретных путей сообщения не обязательно по прямой. Для определения кратчайшего пути коммивояжера будем рассматривать варианты его передвижения последовательно, пункт за пунктом.
Начинаем с вариантов, состоящих из трех участков. Например, отправляясь из исходного пункта A0 можно добраться в третий пункт А3 шестью способами:

Зная расстояния между пунктами, можно вычислить суммарный путь для каждого из шести вариантов.
Результаты рассмотрения сводим в таблицу 1.
Таблица 1 - Перспективы вариантов движения
| Варианты движения | Расстояние, км. | Перспективно или нет |
|
А0 А2 А3 А1 А0 А3 А2 А1 А0 А2 А4 А1 А0 А4 А2 А1 А0 А3 А4 А1 А0 А4 А3 А1 А0 А1 А3 А2 А0 А3 А1 А2 А0 А1 А4 А2 А0 А4 А1 А2 А0 А3 А4 А2 А0 А4 А3 А2 А0 А1 А2 А3 А0 А2 А1 А3 А0 А1 А4 А3 А0 А2 А4 А3 А0 А4 А1 А3 А0 А4 А2 А3 А0 А1 А2 А4 А0 А2 А1 А4 А0 А1 А3 А4 А0 А3 А1 А4 А0 А2 А3 А4 А0 А3 А2 А4 |
650 570 600 470 650 600 900 770 650 420 700 400 470 620 650 550 650 500 570 470 700 850 450 700 |
Нет Да Нет Да Нет Да Нет Да Нет Да Нет Да Да Нет Нет Да Нет Да Нет Да Да Нет Да Нет |
После заполнения таблицы выделяем только перспективные варианты (их будет всего 12), дополняем их номером непосещенного населенного пункта и повторяем процедуру: определяем перспективность движения уже для четырех участков пути. Для этого к вычисленной длине перспективного пути (см. табл. 1) прибавляем расстояние до непосещенного еще населенного пункта. Результаты вычислений заносим в табл. 2.
Таблица 2 - Перспективы выделенных вариантов движения
| Варианты движения | Расстояние, км. | Перспективно или нет |
|
А0 А3 А2 А1 А4 А0 А4 А2 А1 А3 А0 А4 А3 А1 А2 А0 А3 А1 А2 А4 А0 А4 А1 А2 А3 А0 А4 А3 А2 А1 А0 А1 А2 А3 А4 А0 А2 А4 А3 А1 А0 А4 А2 А3 А1 А0 А2 А1 А4 А3 А0 А1 А3 А4 А2 А0 А2 А3 А4 А1 |
770 820 720 1020 570 520 620 900 850 620 950 650 |
Да Нет Да Нет Нет Да Да Нет Нет Да Нет Да |
Аналогично предыдущему из табл. 2 выбираем четыре перспективных варианта.
Так как нам необходимо возвратиться в исходный пункт, то выделенные перспективные последовательности движения дополняем этим исходным пунктом A0. Вычисляем для них суммарные расстояния и заносим результаты в табл. 3.
Таблица 3 – Суммарные расстояния перспективных вариантов движения
| Варианты движения | Расстояние, км. | Перспективно или нет |
|
А0 А3 А2 А1 А4 А0 А0 А4 А3 А1 А2 А0 А0 А4 А3 А2 А1 А0 А0 А1 А2 А3 А4 А0 А0 А2 А1 А4 А3 А0 А0 А2 А3 А4 А1 А0 |
870 870 720 720 920 850 |
Нет Нет Да Да Нет Нет |
Из таблицы видно, что имеется два оптимальных маршрута следования коммивояжера А0 А4 А3 А2 А1 А0 и А0 А1 А2 А3 А4 А0, имеющие минимальную из всех возможных маршрутов длину, равную 720 км.
2. ДИНАМИЧЕСКАЯ ОПТИМИЗАЦИЯ В ПЛАНИРОВАНИИ РАБОТ
Задача 1.10
В условиях задачи производственного планирования (см. МУ [12]) найти оптимальные строки начала строительства каждого из объектов так, чтобы суммарный срок строительства всех объектов был бы минимальным.
Таблица 1.10.10 – Исходные данные
| Объекты | Виды (стадии) работ | |||
| 1 | 2 | 3 | 4 | |
|
А1 |
1 | 2 | 5 | 2 |
|
А2 |
3 | 2 | 3 | 4 |
|
А3 |
2 | 5 | 2 | 4 |
Решение
Считая, что работа на каждом объекте должна продолжаться непрерывно с момента начала строительства до его окончания, требуется определить сроки начала строительства каждого объекта так, чтобы суммарный срок строительства всех объектов был минимальным.
Последовательность строительства может быть любой:

Покажем, как оценивается суммарное время строительства для одного из вариантов, например А1 А2 А3. Сроки окончания работ на первом объекте будут следующими (см. табл. 1.10.10):
-окончание первой стадии 1 месяц;
-окончание второй стадии 1 + 2 = 3 месяца;
-окончание третьей стадии 3 + 5 = 8 месяцев;
окончание четвертой стадии 8 + 2 = 10 месяцев.
Время t2 начала работ на втором объекте должно удовлетворять следующим неравенствам:
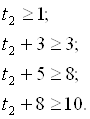
Эти неравенства выражают требования, чтобы каждая из стадий работ на объекте А2 начиналась лишь после окончания работ соответствующих стадий на объекте А1. Одновременно (параллельно) вести один и тот же вид работ у организации нет возможности но условию задачи.
Первое неравенство выражает требование, чтобы первая стадия работ на втором объекте начиналась лишь после окончания первой стадии работ на первом объекте, т.е. через один месяц.
Второе неравенство выражает требование, чтобы вторая стадия работ на втором объекте начиналась лишь после окончания второй стадии работ на первом объекте, т.е. через четыре месяца. При этом надо помнить, что первая стадия работ на втором объекте уже выполнена (t2 +3).
Третье неравенство выражает требование, чтобы третья стадия работ на втором объекте начиналась лишь после окончания третьей стадии работ на первом объекте, т.е. через восемь месяцев (первая и вторая стадии работ на втором объекте уже выполнены, следовательно, t2 +5).
Четвертое неравенство выражает требование, чтобы четвертая стадия работ на втором объекте начиналась лишь после окончания четвертой стадии работ на первом объекте, т.е. через десять месяцев (первая, вторая и третья стадии работ на втором объекте выполнены, следовательно, t2 + 8).
Наименьшее значение t2, удовлетворяющее этим неравенствам, равно 3. Поэтому самый ранний возможный срок начала строительства второго объекта А2 три месяца после начала строительства первого объекта А1. Зная это значение, несложно определить сроки окончания соответствующих стадий работ:
окончание первой стадии 3 + 3 = 6 месяцев;
окончание второй стадии 6 + 2 = 8 месяцев;
окончание третьей стадии 8 + 3 = 11 месяцев;
окончание четвертой стадии 11 + 4 = 15 месяцев.
Зная сроки окончания стадии работ на втором объекте, аналогично определяем срок t3 начала строительства третьего объекта (A3). Для него неравенства будут следующие:
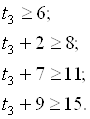
что приводит к минимальному сроку t3 = 6 мес. Следовательно, сроки окончания отдельных стадий строительства третьего объекта будут соответственно:
окончание первой стадии 6 + 2 = 8 месяцев;
окончание второй стадии 8 + 5 = 13 месяцев;
окончание третьей стадии 13 + 2 = 15 месяцев;
окончание четвертой стадии 15 + 4 = 19 месяцев.
Таким образом, для выбранной последовательности строительства объектов А[ А2 А3 общее время строительства (совпадающее со сроком завершения работ на объекте А3) равно 19 мес.
Аналогично определяем сроки и для других оставшихся последовательностей строительства. Результаты заносим в Таблицу.
А1 А3 А2
Стадии А1:
1 – 1 мес.;
2 – 3 мес.;
3 – 8 мес.;
4 – 10 мес..
Неравенства t3:
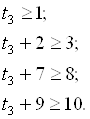
Следовательно, t3 = 1 мес.
Стадии А3:
1 – 3 мес.;
2 – 8 мес.;
3 – 10 мес.;
4 – 14 мес..
Неравенства t2:
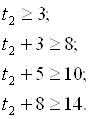
Следовательно, t3 = 6 мес.
Стадии А2:
1 – 9 мес.;
2 – 11 мес.;
3 – 14 мес.;
4 – 18 мес.
Следовательно общее время строительства А1 А3 А2 = 18 мес.
А2 А1 А3
Стадии А2:
1 – 3 мес.;
2 – 5 мес.;
3 – 8 мес.;
4 – 12 мес..
Неравенства t1:
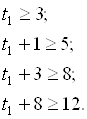
Следовательно, t1 = 5 мес.
Стадии А1:
1 – 6 мес.;
2 – 8 мес.;
3 – 13 мес.;
4 – 15 мес..
Неравенства t3:
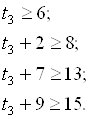














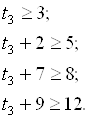
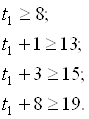
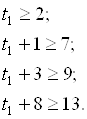
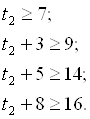
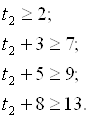
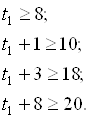
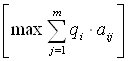 :
: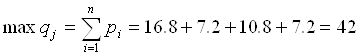
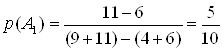
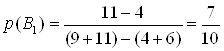
 (zip - application/zip)
(zip - application/zip)










