 Содержание
Содержание
Введение................................................................................
................. 3
Раздел 1. Модели для исследования динамических нагрузок................... 4
Раздел 2. Динамические нагрузки в упругих связях трелевочного трактора
................................................................................
.................................... 21
Раздел 3. Нагрузки при подтаскивании дерева рукоятью..........................
Заключение......................................................................
.......................... 28
Библиографический список................................................................... 29
 Введение
Введение
Определение уровня и характера изменения динамических нагрузок в упругих связях лесосечных машин с помощью тензометрической аппаратуры связано с большой трудоемкостью и зачастую неразрешимыми трудностями, вызванными спецификой труда в лесу. В то же время распространение результатов экспериментальных исследований даже на однотипные лесосечные машины, но с другими параметрами уже не может быть осуществлено в полной мере. Корректные теоретические методы определения динамических нагрузок в упругих связях лесосечных машин свободны от таких недостатков. Поэтому, как уже отмечалось, на данном этапе является актуальным создание основ теории рабочих процессов и методов расчета динамических нагрузок в узлах и элементах конструкций лесосечных машин.
Раздел
1.  Модели для
исследования динамических нагрузок
Модели для
исследования динамических нагрузок
Динамические нагрузки и характер их изменения, как было отмечено выше, могут быть определены в результате составления расчетных схем динамических систем, математического описания их рабочих процессов дифференциальными уравнениями и решения последних. Однако для реальных лесосечных машин полный учет всех факторов приводит к большому числу громоздких уравнений, и найти решение в общем случае не всегда удается. Поэтому во всех случаях целесообразно искать упрощенные и приближенные решения, которые, тем не менее, обладают достаточной для инженерной практики точностью. В связи с этим при выборе расчетной схемы необходимо опираться не только на теоретические обоснования, но и на экспериментальный материал.
Анализ полученных экспериментальных данных и теоретические исследования [1 – 3] позволяют сделать следующее заключение:
при определении динамических колебательных нагрузок лесосечные машины с предметом труда можно рассматривать как линейно-упругие системы;
учитывая, что в процессе естественного эксплуатационного изнашивания в сопряжениях элементов манипулятора и базы возникают люфты и зазоры, а также имеются нелинейности, вызванные различного рода сопротивлениями, лесосечную машину с деревом целесообразно рассматривать в некоторых случаях как нелинейную систему; для определения динамических нагрузок применяют аналоговую вычислительную технику, так как решение нелинейных дифференциальных уравнений аналитическими методами трудоемко, а в некоторых случаях и невозможно;
на осциллограммах экспериментальных исследований наблюдающиеся колебания двух (в отдельных случаях – трех) основных частот соответствуют колебаниям дерева, манипулятора и базы; это обстоятельство дает возможность значительно упростить расчетные схемы динамических систем лесосечных машин, сведя их к трех или двухмассовым.
В соответствии с отмеченным при изучении колебательных динамических нагрузок в упругих связях лесосечных машин можно исходить из расчетной схемы, представленной на рис. 1.1. Расчетная схема может быть упрощена, если учесть, что не все перечисленные элементы оказывают существенное влияние на динамическую нагрузку машины. Так, при работе лесосечной машины влиянием упругих и демпфирующих свойств грунта на ее динамику можно пренебречь. Этот вывод вытекает также из следующих соображений. Приведенная жесткость грунта под опорными частями гусеницы или колесами лесосечных машин составляет соответственно 27000 – 68000 и 10000 – 35000 кН/м. Учет этой жесткости грунта при последовательном соединении ее с жесткостями подвески снижает общую приведенную жесткость базы лишь на 1 – 2%. Поскольку в процессе эксплуатации лесосечные машины шесть – семь месяцев в году работают в зимних условиях, когда жесткость мерзлого грунта больше, то фактическая погрешность определения приведенной жесткости базы практически оказывается еще меньше.
 Следующее упрощение
расчетной схемы возможно за счет пренебрежения влиянием упругих и демпфирующих свойств
кроны пакетируемого с грунта дерева, так как при повале его вследствие удара
вершины о землю происходит разрушение нижней, контактной, части кроны.
Следующее упрощение
расчетной схемы возможно за счет пренебрежения влиянием упругих и демпфирующих свойств
кроны пакетируемого с грунта дерева, так как при повале его вследствие удара
вершины о землю происходит разрушение нижней, контактной, части кроны.
При изучении динамики рабочих процессов лесосечных машин на колесной и гусеничной базах дальнейшее упрощение расчетной схемы возможно на основании работ [18, 38, 41, 46], которые сводятся к следующим положениям:
при изучении низкочастотных колебаний остова трактора влиянием неподрессоренной массы передней части можно пренебречь, так как у колесных тракторов она невелика по сравнению с массой всего трактора;
исследованиями, проведенными в НАТИ, установлено, что демпфирование в подвеске, у колесных тракторов меньше, чем у автомобилей, для которых сопротивлениями в подвеске пренебрегают;
в условиях слабого демпфирования частоты собственных колебаний, вычисленные с учетом сил трения, практически не отличаются от частот свободных колебаний, возникающих при отсутствии неупругих сопротивлений;
при практических расчетах систем подрессоривания гусеничных машин влиянием масс гусениц на момент инерции подрессоренных масс или корпуса машины можно пренебречь;
обобщенные экспериментальные данные качественного характера дают все основания считать системы подрессоривания современных гусеничных машин даже при четко выраженной нелинейности упругих элементов и амортизаторов линейными; в связи с этим при рассмотрении свободных колебаний в переходных режимах лесосечных машин неподрессоренными массами и силами сопротивления рессорной подвески и шин можно также пренебречь.
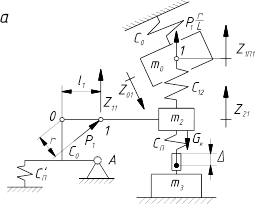
На рис. 1.1 приведены упрощенные расчетные схемы динамических систем.

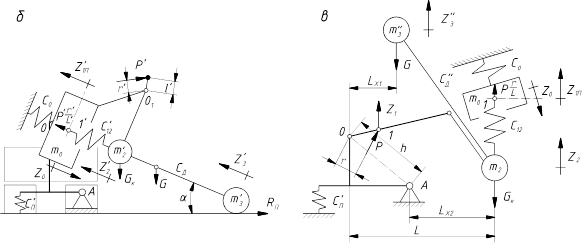
 Рис. 1.1. Исходные расчетные схемы для исследования
нагруженности
Рис. 1.1. Исходные расчетные схемы для исследования
нагруженности
лесосечных машин в режимах подъема (опускания) дерева стрелой (а),
подтаскивания рукоятью (б) и подъема (опускания)
уложенного на рукояти дерева стрелой (в)
Принятые обозначения:
Р, Р" – движущее усилие на штоке гидроцилиндра (гидроцилиндров) подъема стрелы и перемещения рукояти;
r, r/– плечи сил P и Р/ соответственно;
m0 – масса опорно-поворотной конструкции манипулятора и подрессоренной базы, динамически приведенная к оси подвеса рабочего органа;
m2 – масса стрелы, рукояти, захвата (трелевочные тракторы) и стрелы, рукояти, захватно-срезающей головки (валочно-пакетирующие и валочно-трелевочные машины), динамически приведенная к концу рукояти;
m3 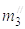 – масса дерева, динамически приведенная в
центр его тяжести;
– масса дерева, динамически приведенная в
центр его тяжести;
 – масса
рукояти, захвата манипулятора (трелевочные тракторы) и рукояти, захватно-срезающей
головки (валочно-пакетирующие и валочно-трелевочные машины), динамически
приведенная к концу рукояти;
– масса
рукояти, захвата манипулятора (трелевочные тракторы) и рукояти, захватно-срезающей
головки (валочно-пакетирующие и валочно-трелевочные машины), динамически
приведенная к концу рукояти;
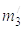 – масса дерева, статически
приведенная к волочащемуся концу дерева;
– масса дерева, статически
приведенная к волочащемуся концу дерева;
m20 – масса стрелы, рукояти, захвата (трелевочные тракторы) и стрелы, рукояти, эахватно-среэающей головки (валочно-пакетирующие и валочно-трелевочные машины), статически приведенная к концу рукояти;
Z0, Z1, Z2, Z3, 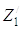 ,
, 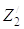 ,
, 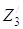 ,
, 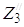 – обобщенные координаты центров приведенных масс m0, m2, m3,
– обобщенные координаты центров приведенных масс m0, m2, m3,  ,
, 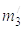 ,
, 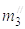 и безмассовых точек 1 и
и безмассовых точек 1 и  ;
;
h – расстояние от точки О до точки А (центра неподвижной системы координат);
l1 – расстояние от точки 1 до точки О (центра подвижной системы координат);
L – вылет манипулятора;
Gк – приведенная сила тяжести металлоконструкции манипулятора;
 с0 – приведенная жесткость опорно-поворотной конструкции
манипулятора;
с0 – приведенная жесткость опорно-поворотной конструкции
манипулятора;
 – приведенная жесткость пружин (рессор) подвески (у
колесных тракторов – жесткость шин);
– приведенная жесткость пружин (рессор) подвески (у
колесных тракторов – жесткость шин);
с12, 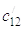 ~ приведенные жесткости стрелы с
рукоятью и рукояти, соответственно;
~ приведенные жесткости стрелы с
рукоятью и рукояти, соответственно;
с3 – приведенная жесткость захватного устройства;
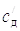 ,
, 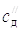 – жесткость (при изгибе) вершинной и
комлевой частей дерева;
– жесткость (при изгибе) вершинной и
комлевой частей дерева;
G – сила тяжести дерева;
l – высота (длина) дерева;
lц – расстояние от точки зажима дерева захватом до центра его тяжести;
hc – расстояние от комля до центра тяжести дерева;
и – длина свеса вершинной или комлевой части дерева;
l/ – расстояние от точки 1 до шарнира О1;
L/ – расстояние от шарнира O1
до центра приведения массы  ;
;
Rп – сила сопротивления перемещению дерева;
Lx1 – расстояние от центра тяжести дерева до центра подвижной системы координат точки О;
Lx2 – расстояние от точки подвеса захватно-срезающего устройства ВПМ или ВТМ до центра неподвижной системы координат точки А;
r0, r01 – радиусы поворота масс m2 и 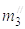 относительно центра неподвижной и подвижной систем
координат соответственно.
относительно центра неподвижной и подвижной систем
координат соответственно.
Как видно из рис. 5.1 расчетные эквивалентные схемы лесосечных машин представлены в виде упругих систем с тремя степенями свободы. При этом приняты некоторые дополнительные допущения [40, 45]:
траектории движения
масс m0, m2, m3,  ,
, 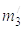 ,
, 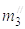 и безмассовых точек 1
и l" в пуско-тормозных режимах прямолинейны;
и безмассовых точек 1
и l" в пуско-тормозных режимах прямолинейны;
величины r, r", L, L" при отрыве дерева от грунта с последующим разгоном и торможением постоянны;
массами подвижных частей гидропривода пренебрегаем ввиду их малости по сравнению с массами стрелы, рукояти и груза;
упругие опоры с одной стороны базы заменяем шарниром.
При принятии допущения о замене задней подвески базы шарниром учитывалось, что в настоящее время в лесной промышленности в основном применяются два серийно выпускаемых трактора – ТДТ-55А и ТТ-4М.
Тракторы ТДТ-55А и ТТ-4М являются базовыми машинами для трелевочных тракторов с манипуляторами, валочно-трелевочных и валочно-пакетирующих машин, а также для целой серии различных погрузчиков.
Как уже отмечалось выше, трелевочный трактор ТДТ-55А
имеет независимую рычажно-балансирную переднюю и заднюю подвески. Каждая
подвеска шарнирно соединена с рамой трактора и подпружинена. Трелевочный
трактор  ТТ-4М также снабжен подвеской
рычажно-балансирного типа, но подпружинены у него только передние каретки, а
задние соединены с рамой шарниром (см. рис. 1.1).
ТТ-4М также снабжен подвеской
рычажно-балансирного типа, но подпружинены у него только передние каретки, а
задние соединены с рамой шарниром (см. рис. 1.1).
Исследованиями [53] установлено, что при замене подпружиненной задней подвески шарниром у лесосечных машин на базе трактора ТДТ-55А (трелевочные с манипуляторами и валочно-трелевочные машины) погрешность определения динамических характеристик составляет не более3-5%.При проектировании же валочно-пакетирующих машин на этой же базе с целью уточнения расчетов может быть использована расчетная схема [53], учитывающая жесткость обеих подвесок.
В то же время опыт создания и эксплуатации валочно-пакетирующих машин ЛП-2 показал, что для придания машине устойчивости в работе необходимы установка аутригеров или блокировка пружин задней подвески, что приводит опять-таки к уже рассмотренным выше расчетным схемам.
Дифференциальные уравнения движения масс систем можно составить в форме уравнений Лагранжа II рода. Для определения деформаций упругих систем, имеющих конечное число степеней свободы (конечное число масс), удобно воспользоваться уравнениями Лагранжа в следующей форме
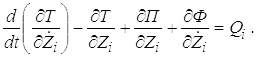 * (1.1)
* (1.1)
Вследствие отсутствия данных о внешних и внутренних демпфирующих сопротивлениях в узлах технологического оборудования лесосечных машин на первом этапе исследований ограничимся учетом диссипативных сил в гидроприводе элементов манипулятора.
Так как все приведенные расчетные схемы лесосечных машин идентичны и описываются уравнениями одного вида, изложим порядок рассуждений при выводе дифференциальных уравнений, описывающих режим подъема (опускания) дерева манипулятором трелевочного трактора (рис. 5.2). Процесс подъема (опускания) дерева стрелой гидроманипулятора можно рассмотреть в три этапа.
На первом этапе (см. рис. 5.2) масса m2 движется под действием постоянной по величине среднепусковой движущей силы P1. Шток гидроцилиндра стрелы воспринимает нагрузку только от массы m20. Масса m3 находится в покое.
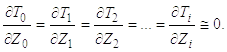
Кинетическая энергия системы

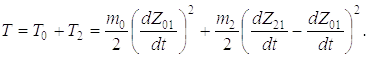 * (1.2)
* (1.2)
Потенциальная ее энергия
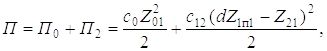 (1.3)
(1.3)
где
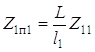 .
.
В выражении (5.2) при рассмотрении движения массы т2 учтены упругие перемещения опорно-поворотной конструкции, так как абсолютная скорость движения массы равна разности скоростей в подвижной системе координат и несущей опорно-поворотной конструкции в неподвижной системе координат.
Дифференцируя Т0 по  и t, Т2 по
и t, Т2 по 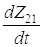 и t,
П0
по Z01, а П2
по Z1п1 и Z21 и, учитывая
внешние силы, получаем систему дифференциальных уравнений
и t,
П0
по Z01, а П2
по Z1п1 и Z21 и, учитывая
внешние силы, получаем систему дифференциальных уравнений
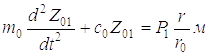 ;
;
(Z1п1 – Z21)с12 = P1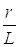 ; (1.4)
; (1.4)
 .*
.*
Здесь m = Lx2 / L.
 |
Рис. 1.2. Эквивалентные расчетные схемы подъема (опускания) дерева
стрелой манипулятора на первом (а), втором (б) и третьем (в) этапах
Для решения системы уравнений (5.4) относительно упругой деформации стрелы-рукояти (Z1п1 – Z21), определяющей нагрузку на конструкцию, нужно знать вид функции движущего или тормозящего усилия f(P), развиваемого гидроприводом машины. Исследованиями [13, 40, 50, 51] установлено, что скорость перемещения поршня в гидроцилиндре может быть определена по формуле
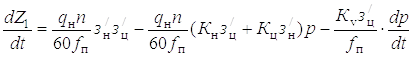 . (1.5)
. (1.5)
где qн – объемная постоянная насоса; n – число оборотов его вала; 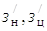 – теоретические объемные КПД насоса с распределителем
и гидроцилиндра; fп – эффективная площадь поршня; Кv, Кн, Кц – коэффициенты пропорциональности; р – давление в гидросистеме
– теоретические объемные КПД насоса с распределителем
и гидроцилиндра; fп – эффективная площадь поршня; Кv, Кн, Кц – коэффициенты пропорциональности; р – давление в гидросистеме
Принимая n = const в период пуска гидропривода, обозначаем
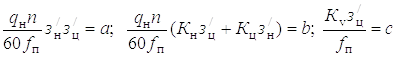 ,
,
 где b, с – коэффициенты, учитывающие удельное изменение
скорости движения поршня вследствие утечек гидрожидкости и упругой ее
деформации.
где b, с – коэффициенты, учитывающие удельное изменение
скорости движения поршня вследствие утечек гидрожидкости и упругой ее
деформации.
Тогда с учетом принятых обозначений можно записать
 . (1.6)
. (1.6)
Выражение (5.6) применим для решения системы уравнений (5.4). Приведя скорость перемещения поршня-штока, жестко связанного с точкой 1, к точке подвеса захвата и заменив усилие в гидроцилиндре подъема стрелы Р произведением давления р на площадь поршня fп, уравнения системы (5.4) и равенство (5.6) на первом этапе запишем в виде
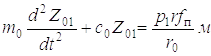 ;
;
(Z1п1
– Z21)с12 =  ; (1.7)
; (1.7)
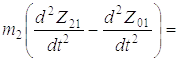 (Z1п1 – Z21)с12 – Gк;
(Z1п1 – Z21)с12 – Gк;
 .
.
Здесь
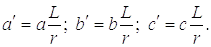
Для упрощения решения системы (5.7), примем допущение, что динамическая деформация опорно-поворотной конструкции мало отличается от ее статической деформации. Это допущение вносит незначительную погрешность в результат исследования [27]. Итак, исходя из допущения
c0Z01 » (Z1п1 – Z21)с12
и дифференцируя дважды по t, находим
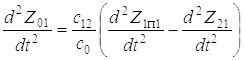 . (1.8)
. (1.8)
Подставляя выражение (5.8) в третье уравнение системы (5.7), получаем

 (Z1п1 – Z21)с12 – Gк. (1.9)
(Z1п1 – Z21)с12 – Gк. (1.9)
Из второго уравнения системы (5.7) представим Z21
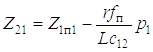 . (1.10)
. (1.10)
Дифференцируя выражение (5.10) по t, имеем
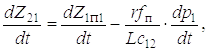
а дифференцируя вторично по t, находим
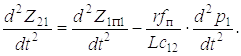
Дифференцируя по t четвертое уравнение системы (5.7), получаем
 (1.11)
(1.11)
Используя допущение
c0Z01 » (Z1п1 – Z21)с12 » 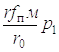 ,
,
запишем p1 в виде

Дифференцируя по t, получаем
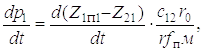 (1.12)
(1.12)
дифференцируя еще раз по t, имеем
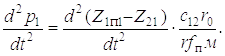 (1.13)
(1.13)
 Значения (5.11) – (5.13) подставляем в выражение для
Значения (5.11) – (5.13) подставляем в выражение для 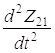
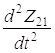 = –
= –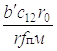 ×
×

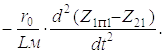 (1.14)
(1.14)
Подставив значение для d2Z2l / dt2 в выражение (5.9), получим дифференциальное уравнение

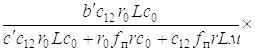

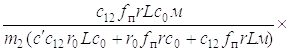
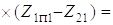
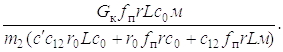 (1.15)
(1.15)
Обозначим
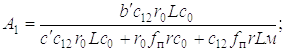

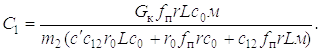
Тогда дифференциальное уравнение (5.15), описывающее движение динамической системы на первом этапе, примет вид
 А1
А1 B1
B1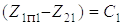 . (1.16)
. (1.16)
 На втором этапе (см. рис. 5.2,б) в упругой связи возникает нагрузка F22, и пока она по величине меньше
статической нагрузки от дерева
На втором этапе (см. рис. 5.2,б) в упругой связи возникает нагрузка F22, и пока она по величине меньше
статической нагрузки от дерева 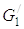 масса m3 находится в состоянии покоя, в движении
находится масса m2. Здесь G¢ = Ghc / (l – u).
масса m3 находится в состоянии покоя, в движении
находится масса m2. Здесь G¢ = Ghc / (l – u).
Составив выражение для кинетической и потенциальной энергии и произведя дифференцирование, как и в первом случае, получим дифференциальные уравнения движения масс системы:
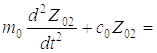


 (1.17)
(1.17)
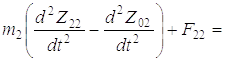
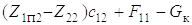 ;
;
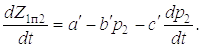
Здесь F01 = c0Z01; F11 = (Z1п1 – Z21)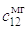 ; F22 = cпZ22; cп – приведенная жесткость захватного
устройства и дерева.
; F22 = cпZ22; cп – приведенная жесткость захватного
устройства и дерева.
Решая систему (5.17) аналогично решению системы (5.7),
получаем дифференциальное уравнение, описывающее движение динамической
системы
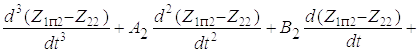
 . (1.18)
. (1.18)
Здесь
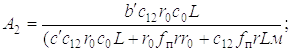

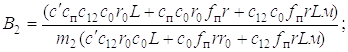
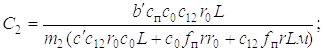

Третий этап характеризуется совместным движением всех масс (см. рис. 1.2, в). На этом этапе пакетируемое дерево оторвано за комель или вершину от грунта по всей длине и поднимается стрелой манипулятора на высоту, необходимую для последующего укладывания его в коник рукоятью. Выполнив названные операции, получим дифференциальные уравнения движения системы на данном этапе
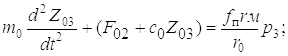
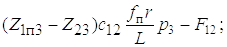
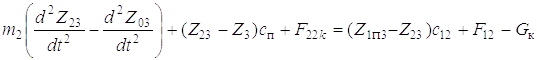 ;
;
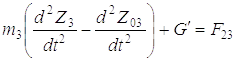 ; (1.19)
; (1.19)

Здесь 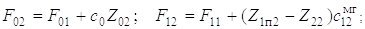

После решения системы (5.19) находим дифференциальное уравнение четвертого порядка, описывающее движение динамической системы:
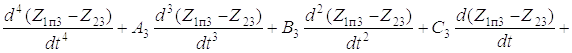
 +
+ 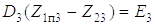 , (5.20)
, (5.20)
где 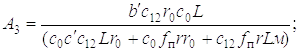
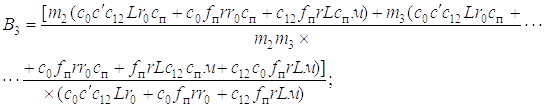
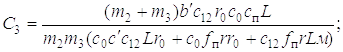

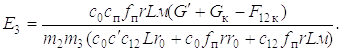
Рассмотрим в качестве примера движение динамической системы на третьем этапе, т.е. решим дифференциальное уравнение (1.20), что позволит расчетным путем определить нагрузку на конструкцию манипулятора и базу, давление в гидроприводе, период, частоту и амплитуду колебаний динамических нагрузок в металлоконструкции и гидроприводе манипулятора. Частное решение этого уравнения
(Z1п3 – Z23) = E3 / D3
представляет собой приведенную статическую деформацию стрелы с рукоятью (ее некоторую часть).
Введя новую переменную
Y1 = (Z1п3 – Z23) – E3 / D3;
получим однородное дифференциальное уравнение
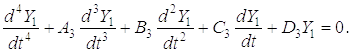 (1.21)
(1.21)
Его характеристическое уравнение будет иметь вид
 x4 + A3x3 + B3x2 + C3x + D3 = 0. (1.22)
x4 + A3x3 + B3x2 + C3x + D3 = 0. (1.22)
Движение рассматриваемой динамической системы происходит с постоянной затратой энергии, расходуемой на преодоление сопротивлений ее движению, и поэтому колебания являются затухающими. В этом можно убедиться, проведя исследование корней характеристического уравнения (5.22) и установив, что вещественная часть всех корней отрицательна.
В случае алгебраических уравнений любой степени n вида
a0xn + a1xn–1 + a2xn–2 +…+ an = 0 (1.23)
с вещественными коэффициентами необходимые и достаточные условия отрицательности вещественных частей всех корней этого уравнения задаются критерием Гурвица [54]. Для того, чтобы все корни уравнения (5.23) при а0 > 1 имели отрицательные вещественные части, необходимо и достаточно, чтобы положительными были следующие определители:


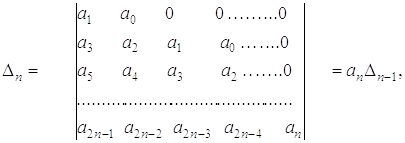
причем ar = 0, если r > п.
В общем виде критерий Гурвица выражается как Di > 0, i = 1,2,...,n.
Для уравнения четвертой степени вида
а0х4 + a1x3 + а2х2 + а3х + а4 = 0,
где a0 = 1, на основании критерия Гурвица должны быть выполнены следующие условия:
1) a1 > 0;
2)

 3)
3) 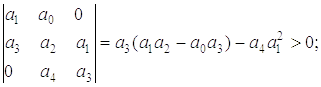
4)
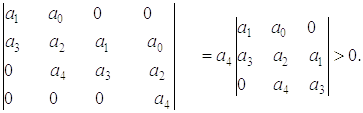
Четвертое условие на основании третьего упрощается: а4 > 0. Так как из третьего условия
следует, что a3(a3a2 – a0a3) > a4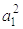 известно, что а4 и (a1a2 – a0a3) > 0, устанавливаем, что а3 > 0. Далее по второму условию получаем,
что a1a2 > а0а3, а так как а0, a1 а3 > 0, то и a2 > 0.
известно, что а4 и (a1a2 – a0a3) > 0, устанавливаем, что а3 > 0. Далее по второму условию получаем,
что a1a2 > а0а3, а так как а0, a1 а3 > 0, то и a2 > 0.
Таким образом критерий Гурвица для уравнения четвертой
степени вида (5.23) формулируется следующим образом: все коэффициенты уравнения
должны быть положительными; a3(a1a2 – a0a3) – a4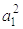 > 0.
> 0.
Исследование коэффициентов уравнения четвертого порядка показало, что они удовлетворяют всем условиям критерия Гурвица. Следовательно, искомое уравнение (5.22) имеет две пары комплексно-сопряженных корней с отрицательными вещественными частями
x1,2 = – a ± ik; x3,4 = –b ± in.
Решение дифференциального уравнения (1.21) имеет вид [54]
Y1 = e–at(C1coskt + C2sinkt) + e–bt(C3cosnt + C4sinnt). (1.24)
Уравнение (5.24) показывает, что в этом случае движение динамической системы можно рассматривать как наложение двух затухающих колебаний.
Для режима торможения стрелы начальные условия могут быть записаны в виде
 (1.25)
(1.25)
где v – приведенная скорость подъема (опускания) дерева, вычисленная по скорости движения штоков гидроцилиндров привода стрелы; tт – время торможения стрелы, определяемое временем переключения золотника распределителя.
 Вычисляя
соответствующие производные и используя начальные условия (5.25), получаем
уравнения для определения произвольных постоянных
Вычисляя
соответствующие производные и используя начальные условия (5.25), получаем
уравнения для определения произвольных постоянных
0 = С1 + С3;
0 = С2k – С1a + C4n – C3b; (1.26)
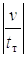 = C1 (a2 – k2) – 2C2ka + C3(b2 – n2) – 2C4nb;
= C1 (a2 – k2) – 2C2ka + C3(b2 – n2) – 2C4nb;
0 = C1 (–a3 + 3k2a) + C2(–k3 + 3ka2) + C3(–b3 + 3n2b) + C4(–n3 + 3nb2).
Отсюда произвольные постоянные определятся выражениями
C1 = D1 / D; C2 = D2 / D; C3 = D3 / D; C4 = D4 / D;
D = nk[(k2 – n2)2 + 2(k2 + n2) (b – a)2 + (b – a)4];
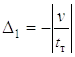 kn[(k2 – n2) – 3(a2 – b2)];
kn[(k2 – n2) – 3(a2 – b2)];
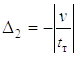 n[3a(k2
+ b2) – a(n2 + a2) – 2b(n2 + b2)];
n[3a(k2
+ b2) – a(n2 + a2) – 2b(n2 + b2)];
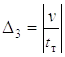 kn[(k2 – n2) – 3(a2 – b2)];
kn[(k2 – n2) – 3(a2 – b2)];
 k[2a(k2
+ a2) – 3b(n2 + a2) + b(k2 + b2)].
k[2a(k2
+ a2) – 3b(n2 + a2) + b(k2 + b2)].
Тогда выражения для определения произвольных постоянных имеют вид
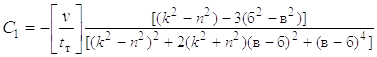 ,
,
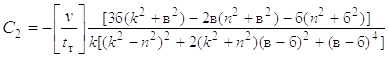 , (1.27)
, (1.27)
 ,
,

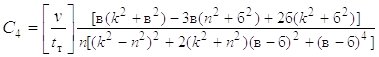 ,
,
где
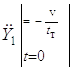 – в режиме
торможения стрелы в конце подъема груза – дерева;
– в режиме
торможения стрелы в конце подъема груза – дерева;
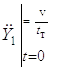 – в режиме
торможения стрелы при опускании груза – дерева.
– в режиме
торможения стрелы при опускании груза – дерева.
Амплитуды колебаний нагрузки выражаются соответственно формулами
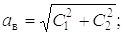
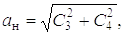 (1.28)
(1.28)
где ав и ан – соответственно амплитуды высокой и низкой частот колебаний.
Очевидно, что при исследовании режима подъем (опускание) груза – дерева стрелой максимальная динамическая нагрузка на конструкцию манипулятора при соотношении частот колебаний 10:1 и более имеет вид
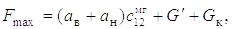 (1.29)
(1.29)
а максимальное давление в гидроцилиндрах стрелы
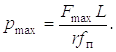 (1.30)
(1.30)
Коэффициент динамичности при этом определяется выражением
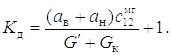 (1.31)
(1.31)
Раздел 2. Динамические нагрузки в упругих связях трелевочного
трактора
Нагрузки при разгоне и торможении дерева стрелой. Как уже отмечалось, наиболее тяжелыми режимами работы трелевочного трактора с манипулятором в процессе набора пачки деревьев являются переходные пуско-тормозные режимы.
Именно в этих случаях на манипулятор воздействуют максимальные пиковые динамические нагрузки.
 Режим разгона у современных лесосечных машин
манипуляторного типа протекает более благоприятно. Это связано прежде всего с
тем, что время разгона в среднем в 1,4-1,7 раза превышает время торможения
элементов манипулятора. Длительность его зависит от параметров дерева, с
увеличением объема которого процесс разгона, затягивается и протекает без
значительных колебаний нагрузки.
Режим разгона у современных лесосечных машин
манипуляторного типа протекает более благоприятно. Это связано прежде всего с
тем, что время разгона в среднем в 1,4-1,7 раза превышает время торможения
элементов манипулятора. Длительность его зависит от параметров дерева, с
увеличением объема которого процесс разгона, затягивается и протекает без
значительных колебаний нагрузки.
При необходимости форсирования работы машины в указанном режиме задача определения динамических нагрузок сводится к решению полученных выше дифференциальных уравнений при заданных начальных условиях. Особо следует остановиться на таких режимах работы трелевочного трактора, как разгон «с веса» и отрыв дерева или пачки от грунта (подъем «с подхватом»), которые также сопровождаются значительными динамическими нагрузками.
Разгон «с веса». В процессе взаимодействия трелевочного трактора с деревом (деревьями) этот режим не является основным, но часто применяется операторами вследствие затруднений при наборе пачки, вызванных завалом соседними деревьями, когда пакетируемое дерево приходится вытаскивать несколькими приемами путем чередования операций подъема и подтаскивания. Общее решение дифференциального уравнения (1.20) в этом случае равно сумме решений однородного уравнения и частного решения
Y = Y1 + Y2
или
Y1 = e–at(C1coskt + C2sinkt) + e–bt(C3cosnt + C4sinnt) +  (2.1)
(2.1)
Начальные условия однородного уравнения запишутся в виде
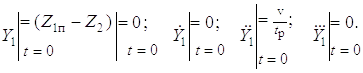 (2.2)
(2.2)
Здесь tp – время разгона стрелы манипулятора.
Произвольные постоянные, амплитуды, колебаний нагрузки и другие динамические характеристики определяются соответственно выражениями (1.27) – (1.31).
Подъем «с подхватом». При работе трелевочного трактора с манипулятором имеет место «равномерный подхват». Он происходит в момент начала подъема дерева, когда захват еще только поворачивается относительно рукояти, а манипулятор уже перемещается с некоторой скоростью. В этом режиме работы (см. рис. 1.2,а) начальные условия могут быть представлены
 (2.3)
(2.3)
 Решение
дифференциального уравнения (5.20) без правой части запишется как
Решение
дифференциального уравнения (5.20) без правой части запишется как
Y1 = e–at(C1coskt + C2sinkt) + e–bt(C3cosnt + C4sinnt).
Произвольные постоянные определятся следующими выражениями:

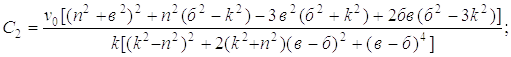
 (2.4)
(2.4)

Динамические характеристики находят по ранее установленным зависимостям (1.27) – (1.31).
Пример определения динамических нагрузок на манипулятор трелевочного трактора.Рассмотрим процесс торможения стрелы трелевочного трактора ТБ-1 в конце подъема дерева за комель. Манипулятор и привод трактора ТБ-1 имеют следующие параметры: L = 5 м; r = 0,35 м; r0 = 3,04 м; l1 = 0,94 м; h = 3 м; fп = 226 см2;
qн = 50 см3/об, 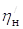 = 0,85;
= 0,85; 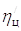 = 0,95; tт = 0,15 с. Частоту вращения коленчатого
вала двигателя принимаем равной 157 с–1
(1500 об/мин), объем пакетируемого дерева – 2,00 м3 (G = 16 кН).
= 0,95; tт = 0,15 с. Частоту вращения коленчатого
вала двигателя принимаем равной 157 с–1
(1500 об/мин), объем пакетируемого дерева – 2,00 м3 (G = 16 кН).
1. Вычисляем параметры, входящие в коэффициенты А3 В3 С3 и D3 дифференциального уравнения (1.20). Полученные данные запишем в следующем виде:
m2, кг.................….246
m.....................…….0,454 – 0,706 a", м/с......................…0,66
с12, кН/м..............…372,30 b", см3/(с×Н).................0,029
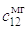 , кН/м.................290,60 v, м/с......................…..0,50
, кН/м.................290,60 v, м/с......................…..0,50
с0, кН/м...............….554,34 m3, кг.....................…...1180
с", см3/Н...............….0,00035 G"+ Gк, кН...................11,48
 2. Подставляя вычисленные значения исходных параметров
в выражения для А3, В3, С3 и D3, получаем А3 = 3,89, В3 = 1032,38, С3 = 813,1,
2. Подставляя вычисленные значения исходных параметров
в выражения для А3, В3, С3 и D3, получаем А3 = 3,89, В3 = 1032,38, С3 = 813,1,
D3 =
31385.
Так как эти коэффициенты удовлетворяют всем условиям критерия Гурвица, то
x1,2 = –a ± ik; x3,4 = –b ± in.
3. Корни уравнения можно определить приближенно по методу Лобачевского–Греффе [17] или используя методику [39]:

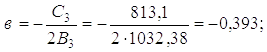
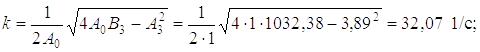
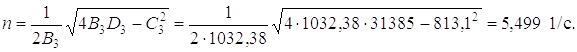
Таким образом, имеем
x1,2 = –1,945 ± 32,07i; x3,4 = –0,393 ± 5,499i.
4. Используя выражения (5.27), находим значения произвольных постоянных: C1 = 0,329, С2 = – 0,063, С3 = – 0,329, С4= 0,275.
5. Определяем упругую деформацию участка стрела – рукоять, ускорение деформации и добавочную динамическую нагрузку на манипулятор трелевочного трактора:
Y1 = (Z1п – Z2) = e–at(C1coskt + C2sinkt) + e–bt(C3cosnt + C4sinnt);
 = e–at{[a(C1k + C2a) –k(C2k – C1a)]sinkt – [a(C2k – C1a) +
= e–at{[a(C1k + C2a) –k(C2k – C1a)]sinkt – [a(C2k – C1a) +
+k(C1k + C2a)]coskt}+ e–bt{[b(C3n + C4b) –n(C4n – C3b)]sinnt – [b(C4n – C3b)+
+ n(C3n + C4b)]cosnt}.
Так как в рассматриваемом случае 32, 07:5, 499 < 10:1, то добавочную нагрузку находим как
 |
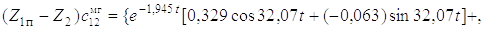
+ 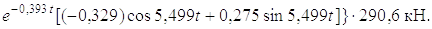
Задавая время t, находим, что максимальная деформация участка стрела – рукоять достигает 0,51 см (рис. 5.3). При этом добавочная нагрузка составит 1,482 кН.
6. Находим коэффициент динамичности
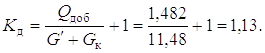
Раздел 3. Нагрузки при подтаскивании дерева рукоятью
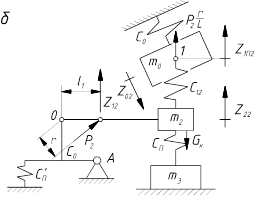
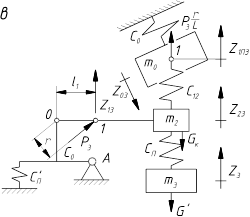
На рис. 1.1, б приведена расчетная схема, соответствующая данному режиму работы.
Кинетическая энергия системы
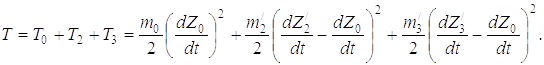
Потенциальная энергия
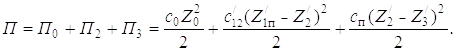
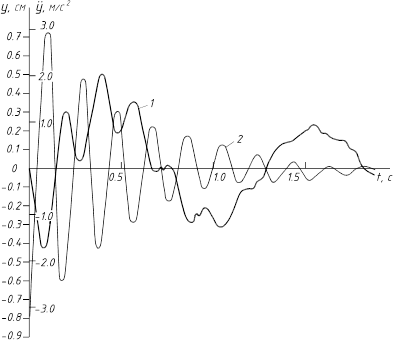
Рис. 3.1. График изменения деформации (1)
и ускорения (2) участка стрела – рукоять
 Дифференцируя T0 по
Дифференцируя T0 по 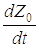 и t, T2 по
и t, T2 по 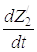 и t, T3 по
и t, T3 по 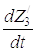 и t, а П соответственно по Z0,
и t, а П соответственно по Z0, 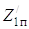 ,
, 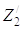 и
и 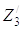 и учитывая внешние силы, получим систему
дифференциальных уравнений
и учитывая внешние силы, получим систему
дифференциальных уравнений
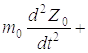 c0Z0 =
c0Z0 = 
(Z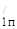 – Z
– Z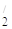 )c
)c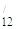 =
= 
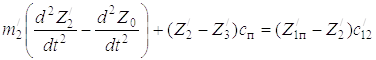 ; (3.1)
; (3.1)
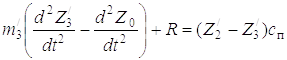 .
.
Здесь
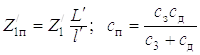 .
.
 Присоединяя уравнение связи
Присоединяя уравнение связи
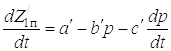
и преобразуя систему (5.36), получим дифференциальное уравнение аналогичное уравнению (5.20), отличающееся лишь коэффициентами
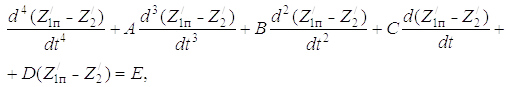 (3.2)
(3.2)
где
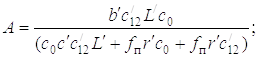
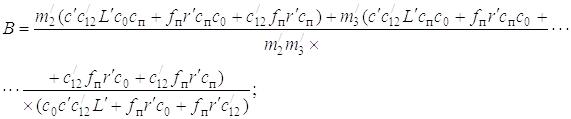
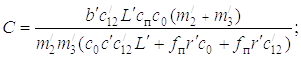
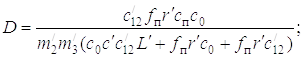
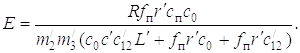
Как видим, и процесс подтаскивания дерева рукоятью может быть описан математически.
В этом режиме работы максимальная динамическая нагрузка в упругой связи
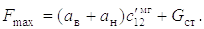
Статическая нагрузка на рукоять определится по формуле
 Gст = (Gк + G)sina + Rп / cosa,
Gст = (Gк + G)sina + Rп / cosa,
где Rп = (1 – n)Gfв; n – коэффициент, учитывающий, какая часть дерева приходится на рабочий орган; fв – коэффициент сопротивления перемещению дерева по грунту.
Максимальное давление в гидроцилиндре рукояти определится выражением
pmax = Fmax L¢ / r¢fп.
Коэффициент динамичности будет равен
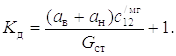
 Заключение
Заключение
Расчеты, выполненные в работе помогли установить, что нагруженность лесосечных машин с манипуляторами во многом зависит от массы и жесткости элементов технологического оборудования и базовых машин. С уменьшением массы и жесткости элементов машин динамические нагрузки снижаются. Поэтому при создании новых лесосечных машин необходимо стремиться к уменьшению их массы и жесткостей всей системы или отдельных ее элементов.
Список литературы
1. Александров В.А. Динамические нагрузки в лесосечных машинах. – Л.: ЛГУ, 1984. 152 с.
2. Александров В.А. Моделирование взаимодействия лесных машин с предметом труда и внешней средой. – Л.: ЛТА, 1987. 80 с.
3. Александров В.А., Демаков В.М. Нагрузки в рубильных установках // Межвуз. сб. научн. трудов / ЛТА. Л., 1989. С. 4-8.
4. Анапольская Л.Е., Гандин Л.С. Методика определения расчетных скоростей ветра для проектирования ветровых нагрузок на строительные сооружения // Метрология и гидрология. 1958. № 10. С. 10-17.
5. Андрианова В.Е. Деятельность человека в системах управления. Л.; ЛГУ, 1974. 133 с.
6. Барановский В.А., Некрасов P.M. Системы машин для лесозаготовок. М.: Лесн. пром-сть, 1977. 248 с.
7. Богачев С.К. Авиационная эргономика. М., 1978. 135 с.
8. Брауде В.И. Вероятностные методы расчета грузоподъемных машин. Л. 1978. 230 с.
9. Брейтер B.C. Статистическое моделирование эксплуатационных параметров деревьев в различных районах страны / Перспективная технология и организация производства: Тр. ЦНИИМЭ. Химки, 1977. С. 38-49.
10. Бурмак П.С. Исследование устойчивости валочно-пакетирующих машин против опрокидывания: Автореф. канд. дисс. Л., 1976. 19 с.
11. Введение в эргономику / Под ред. В.П. Зинченко. М.: «Советское радио», 1974. 349 с
12. Виногоров Г.К. Лесосечные работы. М.: Лесн. пром-сть, 1981. 272 с.
13. Гамынин Н.С. Основы следящего гидравлического привода. М.: Оборонгиз, 1962. 294 с.
 14. Гоберман Л.А.
и др. Теория конструкции и расчет строительных и дорожных машин. М.:
Машиностроение, 1979. 406 с.
14. Гоберман Л.А.
и др. Теория конструкции и расчет строительных и дорожных машин. М.:
Машиностроение, 1979. 406 с.
15. Дебердеев А.А. К вопросу о центре тяжести и моменте инерции дерева // Лесной журнал. 1966. № 6. С. 53-63.
16. Дебердеев А.А. Определение угловой скорости свободно падающего дерева // Лесной журнал. 1967. № 1. С. 42-49.
17. Демидович Б.П. и Марон И.А. Основы вычислительной математики. М.: Наука, 1970. 664 с.
18. Дмитриев А.А., Чобиток В.А., Тельминов А.В. Теория и расчет нелинейных систем подрессоривания гусеничных машин. М.: Машиностроение, 1976. 203 с.
19. Добрынин Ю.А. Исследование вертикальной динамики колесного трактора на трелевке леса в условиях рубок промежуточного лесопользования: Автореф. дисс. Л., 1973. 19 с.
20. Долговых Г.П. Комплексные характеристики лесного фонда лесозаготовительных районов страны // Тр. ЦНИИМЭ. Химки, 1977. С. 30-37.
21. Древесина. Показатель физико-механических свойств. М.: Изд-во стандартов, 1962.
22. Житомирский В.К. Механические колебания и практика их устранения. М.: Машиностроение, 1966. 174 с.
23. Закревский П.Б., Полищук А.П. Определение момента инерции дерева и объемного веса кроны // Тр. ЦНИИМЭ. Химки. № 109. 1970. С. 125-127.
24. Jlinen A. The mechanical theory of trees. Helsinki, 1954.
25. Клепиков Н.Л. Оценка микропрофиля трелевочных волоков и лесовозных дорог в условиях рубок промежуточного пользования // Межвуз. сб. научн. тр. ЛТА. Л., 1987. С. 34-37.
26. Кобринский А.Е., Степаненко Ю.А. Некоторые проблемы теории манипуляторов // Механика машин. М.: Наука, 1967. Вып. 7-8. С. 4-23.
27. Комаров М.С. Динамика грузоподъемных машин. М.: Машгиз, 1962. 267 с.
28. Кричевский Ю.М. Влияние климата на надежность машин и механизмов. Минск: Изд-во «Наука и техника», 1967. 87 с.
29. Ляликов А.П. Человек – электроника – корабль. Л., 1978. 278 с.
30. Леонтьев Н.Л. О влажности и объемном весе древесной кроны // Тр. ЦНИИМЭ. Химки, 1967.№ 84. С. 125-134.
31. Мелик-Гайказов В.И. и др. Гидропривод тяжелых грузоподъемных машин и самоходных агрегатов. М.: Машиностроение, 1968. 263 с.
32. Невзоров Л.А., Зарецкий А.А., Волин Л.М. и др. Башенные краны. М.: Машиностроение, 1979. 292 с.
33. Орлов М.М. Лесная вспомогательная книжка для таксации и технических расчетов. М.-Л.: Сельколхозгиз, 1931. 729 с.
34. Орлов С.Ф. Теория и применение агрегатных машин на лесозаготовках. М.: Гослесбумиздат, 1963. 271 с.
35. Петруша Г.Н. Некоторые вопросы взаимодействия хлыстов с трелевочными механизмами // Тр. ЛТА. 1959. № 83. С. 83-98.
 36. Полищук А.П. Валка
леса. М.: Лесн. пром-сть, 1972. 172 с.
36. Полищук А.П. Валка
леса. М.: Лесн. пром-сть, 1972. 172 с.
37. Полищук А.П. Эксплуатационные показатели деревьев и древостоев лесного фонда СССР / Тр. ЦНИИМЭ. Химки, 1968. 59 с.
38. Попов Д.А., Попов Е.Г., Волошин Ю.А. и др. Системы подрессоривания современных тракторов. М.: Машиностроение, 1974. 172 с.
39. Проектирование системы ручного управления космических кораблей. Под ред. В.А. Климова. М.: Машиностроение, 1978. 141 с.
40. Рахманин Г.А. Исследование динамики погрузочного устройства манипуляторного типа с гидравлическим приводом // Тр. ЦНИИМЭ. Химки. № 91. С. 88-99.
41. Ротенберг Р.В. Подвеска автомобиля. М.: Машиностроение, 1972. 329 с.
42. Рыскин Ю.Е. Исследование вопросов плавности хода лесного колесного тягача: Автореф. канд. дисс. Л., 1974. 21 с.
43. Рыскин Ю.Е. Особенности микропрофиля трелевочных волоков и их статистические характеристики // Тр. ЦНИИМЭ, Химки. № 103. С. 148-157.
44. Старков Г.И. Аэродинамическая характеристика дерева // Тр. ЦНИИМЭ. Химки, 1966. № 71. С. 3-28.
45. Тимошенко С.П. Колебания в инженерном деле. М.: Физматгиз, 1959. 436 с.
46. Толъский В.Е., Корчемный Л.В., Латышев Г.В. и др. Колебаний силового агрегата автомобиля. М.: Машиностроение, 1976. 226 с.
47. Тюрин А.В. и др. Лесная вспомогательная книжка. М.-Л.: Гослесбумиздат, 1956. 532 с.
48. Тюрин А.В. Таксация леса. М.: Гослесбумиздат, 1945. 376 с.
49. Федин В.В. Исследование момента от ветровой нагрузки на деревья применительно к работе лесозаготовительных валочных машин: Автореф. канд. дисс. Л., 1973. 19 с.
50. Хаймович Е.М. Гидроприводы и гидроавтоматика станков. М.: Машгиз, 1959. 555 с.
51. Хохлов В.А. Гидравлические усилители мощности. М.: Изд-во АН СССР, 1963. 104 с.
52. Химмелъблау Д. Прикладное нелинейное программирование / Пер. с англ. М., 1975. 534 с.
53. Чернцов В.А., Александров В.А. К анализу расчетных схем для приведения жесткости подвесок базы лесной машины // Лесной журнал, 1978. № 6. С. 37–41.
54. Яблонский А.А., Норейко С.С. Курс теории колебаний. М.: Высшая школа, 1961. 206 с.
55. Яценко Н.И., Прутчиков O.K. Плавность хода грузовых автомобилей. М.: Машиностроение, 1969. 220 с.
56. Силаев А.А. Спектральная теория подрессоривания транспортных машин. М.: Машиностроение. 1971. 241 с.
 57. Сенников В.В.
Разработка и обоснование основных проектных параметров устройства для рубок
ухода с разделкой деревьев в близком к вертикальному положении. Автореферат
дисс. на соиск. уч. степени канд. техн. наук, В.В. Сенников. С.Пб.: ЛТА, 1992.
17 с.
57. Сенников В.В.
Разработка и обоснование основных проектных параметров устройства для рубок
ухода с разделкой деревьев в близком к вертикальному положении. Автореферат
дисс. на соиск. уч. степени канд. техн. наук, В.В. Сенников. С.Пб.: ЛТА, 1992.
17 с.
58. Шипилин Н.А. Экспериментальное исследование процесса срезания сучьев при силовом резании / Н.А. Шипилин // Вопросы механизированной обрезки сучьев. Химки: Труды ЦНИИМЭ № 79, 1967. С. 60-77.
59. Некрасов Р.М. Исследование процесса срезания сучьев при переменной скорости подачи стволов / Р.М. Некрасов, Ю.В. Плотников // Вопросы механизированной обрезки сучьев. Химки: Труды ЦНИИМЭ. № 79, С. 78–90.
60. Некрасов Р.М. О построении модели расчетного дерева применительно к обрубке сучьев. Химки. Труды ЦНИИМЭ. № 79, 1967. С. 94-119.
61. Кушляев В.Ф. Лесозаготовительные машины манипуляторного типа. М., Лесн. пром-сть, 1981. 248 с.
62. Дитрих В.И. Основы проектирования сучкорезных машин: Автореферат дисс. на соиск. уч. степени д-ра. техн. наук / В.И. Дитрих. – Красноярск, СГТУ, 2001. – 55с.
 63. Александров
В.А., Третьяков В.И. Анализ нагруженности элементов конструкции
лесопосадочных агрегатов при технологических переездах. С.Пб.: Изд-во С.Пб.
ГЛТА 1996. С. 143-151.
63. Александров
В.А., Третьяков В.И. Анализ нагруженности элементов конструкции
лесопосадочных агрегатов при технологических переездах. С.Пб.: Изд-во С.Пб.
ГЛТА 1996. С. 143-151.
64. Максимов Л.П. Повышение технико-экономических показателей валочно-пакетирующих машин за счёт более эффективного использования мощности силовых установок в технологическом цикле: Автореферат дисс. на соиск. уч. степени канд. техн. наук Химки: ЦНИИМЭ, 1985. – 20 с.
65. Александров В.А., Трусовцев Д.С. Нагруженность валочно-пакетирующих машин в режимах стопорения при выравнивании платформы. С.Пб.: Изд-во С.Пб. ГЛТА 2002. С 182-187.
66. Гусев В.А., Александров В.А. Нагруженность силовой установки валочно-пакетирующей машины в режимах стопорения при выравнивании платформы. С.Пб.: Изд-во С.Пб. ГЛТА 2002. С. 66-73.
*При использовании уравнений Лагранжа к решению задачи малых колебаний соответственно [27]
*Здесь и далее последние цифровые индексы буквенных обозначений Z0, Z1п, Z2, P, F0, F1 и F2 соответствуют перемещениям и силам, воспринимаемым массами на соответствующих этапах движения системы.
.














 (zip - application/zip)
(zip - application/zip)











