Многочлены. Преобразование координат

Реферат по дисциплине «Алгебра и геометрия»

на тему:

«Многочлены. Преобразование координат»

Выполнил

студент 1 курса ВятГУ

группа ИВТ-11

Обухов Алексей Игоревич

Номер зачетной книжки: Д10-ФАВТ-2012-75

Киров 2012

I. Многочлены.

Определение.

Многочленом (или полиномом) n-й степени от неизвестного х называется выражение вида: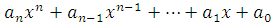

(сумма неотрицательных степеней неизвестного х, взятых с некоторыми коэффициентами, где ).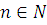

Связанные определения:

·        Многочлен вида 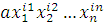  называется одночленом или мономом мультииндекса  

       .

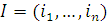·        Степенью многочлена называется максимальная из степеней его одночленов, тождественный нуль не имеет степени.

·        В случае, когда многочлен имеет всего два ненулевых члена, его называют двучленом или биномом.

·        В случае, когда многочлен имеет всего три ненулевых члена, его называют трёхчленом.

·        Коэффициенты многочлена обычно берутся из определённого коммутативного кольца R (чаще всего поля, например, поля вещественных или комплексных чисел).

Действия над многочленами:

1.     Суммой двух многочленов A(x) и B(x)  называется многочлен, у которого коэффициент при каждой степени х равен сумме коэффициентов при той же степени в многочленах A(x) и B(x).

2.     Чтобы перемножить два многочлена A(x) и B(x), нужно каждый член многочлена A(x) умножить на каждый член многочлена  B(x) и полученные результаты сложить.

3.     Пусть A(x) = B(x)•C(x), A(x)  и B(x) - два многочлена, причем степень многочлена A(x) не меньше степени многочлена B(x). Если существует такой многочлен C(x), что выполняется равенство A(x) = B(x)•C(x), то говорят, что многочлен A(x) делится нацело на многочлен B(x). A(x), B(x), C(x) называются соответственно делимое, делитель, частное. Если такого многочлена не существует, то многочлен A(x) не делится на B(x). В этом случае, как и при рассмотрении деления с числами, производится деление с остатком.

Схема Горнера.

Для деления многочлена n-й степени  на многочлен первой степени (x−c)  можно использовать метод сокращенного деления - схему Горнера. При делении многочлена n-й степени на линейный двучлен (x−c)  в остатке может получиться либо многочлен нулевой степени (т.е. отличное от нуля число), либо нуль, а степень частного равна (n−1) . 
Пусть частное многочленов P(x) и (x−c)  имеет вид:

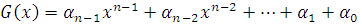
а остаток R(x) равен числу β. Для рассматриваемого случая формула P(x)=Q(x)•G(x)+R(x) принимает вид:

 

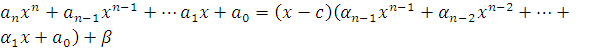
Раскрывая скобки и приводя подобные члены в правой части равенства, на основании определения равенства многочленов получим систему линейных уравнений для нахождения коэффициентов :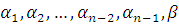

…

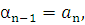
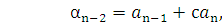
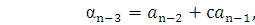
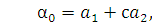
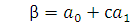
Первое уравнение системы дает значение 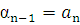. Подставляя это значение  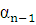во второе уравнение системы, получаем 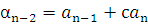. Подставляя полученное значение  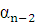в третье уравнение системы, получаем значение  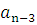и т.д. Последним будет найдено выражение для остатка β:

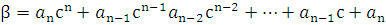
Теорема Безу.

Многочлен  при делении на (x−c)  дает остаток, равный значению этого многочлена при x=c

Основная теорема алгебры.

Всякий многочлен n-й степени с комплексными коэффициентами в множестве комплексных чисел имеет ровно n корней, если каждый кратный корень считать такое число раз, какова его кратность.
Все доказательства этой теоремы (а их найдено весьма много) основаны на использовании свойства непрерывности множества действительных и комплексных чисел, вследствие чего все эти доказательства нельзя считать чисто алгебраическими.
Основная теорема алгебры справедлива и при (n=0), так как многочлен нулевой степени корней не имеет. Основная теорема алгебры неприменима лишь к нулевому многочлену (числу нуль), степень которого не определена.

Теорема Виета

Если 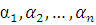  — корни многочлена ,(каждый корень взят соответствующее его кратности число раз), то коэффициенты 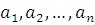 выражаются в виде симметричных многочленов от корней, а именно:

…

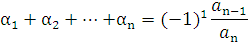
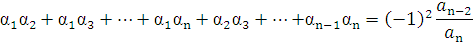
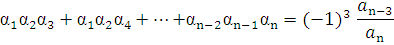
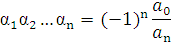
Если старший коэффициент многочлена 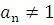, то для применения формулы Виета необходимо предварительно разделить все коэффициенты на  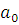(это не влияет на значение корней многочлена). В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему. Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленен.

II. Преобразование координат

1.     Преобразование декартовых координат при параллельном сдвиге осей определяется формулами:

  ,   .

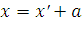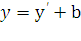Здесь x, y - координаты произвольной точки М плоскости относительно старых осей, ,  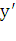- координаты той же точки относительно новых осей, a, b - координаты нового начала  относительно старых осей (говорят также, что a - величина сдвига в направлении оси абсцисс, b - величина сдвига в направлении оси ординат).

2.     Преобразование декартовых прямоугольных координат при повороте осей на угол α (который надо понимать, как в тригонометрии) определяется формулами

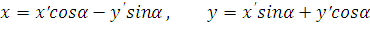
Здесь  x , y  – это координаты произвольной точки М плоскости относительно стар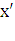ых осей, ,  - координаты той же точки относительно новых осей.

3.     Формулы

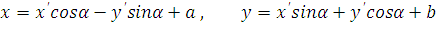
определяют преобразование координат при параллельном сдвиге системы осей на величину а в направлении Ох, на величину b в направлении Оу и последующем повороте осей на угол α. Все указанные формулы соответствуют преобразованию координат при неизменном масштабе.

Литература

·               Прасолов В.В. Многочлены. 3-е изд. исправленное.- М.: МЦНМО, 2003г.

·               Шувалова Э. З., Агафонов Б. Г., Богатырёв Г. И.  Повторим математику. Издательство  «Высшая школа» 1968г.

·               Александров П.С. Курс аналитической геометрии и линейной алгебры. Москва «Наука» 1979г.

·               Материал лекций.