Методы оптимизации функций одной переменной

Автономное образование учреждение высшего профессионального образования   

           Курская академия государственной и муниципальной службы.

 Кафедра «Информационной и техносферной безопасности и правовой защиты

                                                      информации».

Реферат по дисциплине «Методы оптимальных  

                      решений» на тему:

«Методы оптимизации функций одной переменной».

                                                                                         Выполнила студентка

                                                                                
                        2 курса гр. «экономика – 411»

                                                                                                        Сайкова А. А.

                                                                                
                        Проверил преподаватель

                                                                                
                        Погосян С. Л.

                                                           2012

Содержание.

1.     Дифференцируемая функция……………………………………... 3

2.     Непрерывность дифференцируемой функции…………………... 4

            Примеры непрерывности дифференцируемой функции…………... 6

3.     Экстремум максимум и минимум функции……………………... 8

4.     Метод Лагранжа………………………………………………….. 11

5.     Исследование функции одной переменной……………………... 16

            Примеры функции одной переменной……………………………… 18

6. Список используемой литературы……………………………….. 20

Дифференцируемая функция.

Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция — это функция, дифференцируемая в каждой точке данного множества.

Дифференцируемость является одним из фундаментальных понятий в математике и имеет значительное число приложений как в самой математике, так и в других естественных науках.

Приращение дифференцируемой в данной точке функции можно представить как линейную функцию приращения аргумента с точностью до величин более высокого порядка малости. Это означает, что для достаточно малых окрестностей данной точки функцию можно заменить линейной (скорость изменения функции можно считать неизменной). Линейная часть приращения функции называется ее дифференциалом (в данной точке).

Необходимым, но не достаточным условием дифференцируемости является непрерывность функции. В случае функции от одной вещественной переменной дифференцируемость равносильна существованию производной.

В случае функции нескольких вещественных переменных необходимым (но не достаточным) условием дифференцируемости является существование частных производных по всем переменным.

Для дифференцируемости функции нескольких переменных в точке достаточно, чтобы частные производные существовали в некоторой окрестности рассматриваемой точки и были непрерывны в данной точке.

В случае функции комплексной переменной дифференцируемость в точке часто называется моногенностью и существенно отличается от понятия дифференцируемости в вещественном случае. Ключевую роль в этом играет так называемое условие Коши — Римана. Функция, моногенная в окрестности точки, называется голоморфной в этой точке.

В функциональном анализе существует обобщение понятия дифференцирования на случай отображений бесконечномерных пространств — производные Гато и Фреше.

Непрерывность дифференцируемой функции.

Функция y=f(x) называется дифференцируемой в некоторой точке x0, если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна.

Таким образом,из дифференцируемости функции следует ее непрерывность.

Доказательство. Если 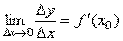, то 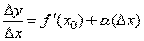, где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда

Δy=f "(x0) Δx+αΔx=> Δy→0 при Δx→0, т.е f(x) – f(x0)→0 при x→x0, а это и означает, что функция f(x) непрерывна в точке x0. Что и требовалось доказать.

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

Рассмотрим на рисунке точки а, b, c.

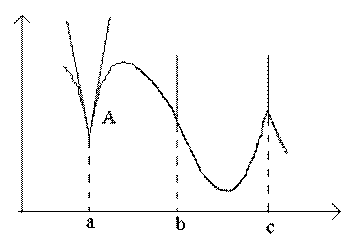
В точке a при Δx→0 отношение 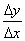 не имеет предела (т.к. односторонние пределы различны при Δx→0–0 и Δx→0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к1 и к2. Такой тип точек называют угловыми точками.

В точке b при Δx→0 отношение 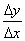 является знакопостоянной бесконечно большой величиной  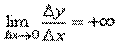. Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – "точка перегиба" c вертикальной касательной.

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиеся вертикальные касательные. Тип – "точка возврата" с вертикальной касательной – частный случай угловой точки.

Примеры непрерывности дифференцируемой функции.

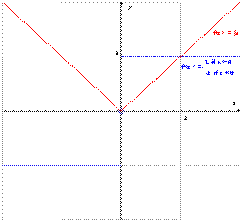
1. Рассмотрим функцию y=|x|.

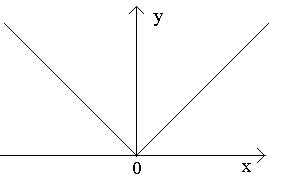
Эта функция непрерывна в точке x = 0, т.к.

.

Покажем, что она не имеет производной в этой точке.

f(0+Δx) = f(Δx) = |Δx|. Следовательно, Δy = f(Δx) – f(0) = |Δx|

Но тогда при Δx< 0 (т.е. при Δx стремящемся к 0 слева)

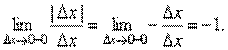
А при Δx > 0,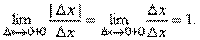

Так как, 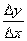 при Δx→ 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x| в точке x= 0 не существует. Геометрически это значит, что в точке x= 0 данная "кривая" не имеет определенной касательной (в этой точке их две).

2. Функция 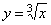 определена и непрерывна на всей числовой прямой.

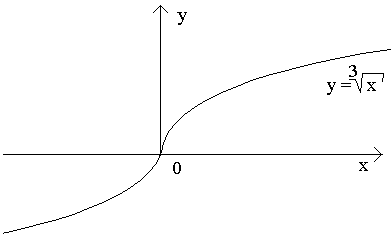
Выясним, имеет ли эта функция производную при x= 0.

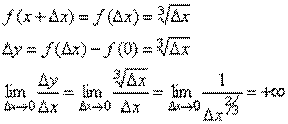
Следовательно, рассматриваемая функция не дифференцируема в точке x= 0. Касательная к кривой в этой точке образует с осью абсцисс угол p/2, т.е. совпадает с осью Oy.

Экстремум максимум и минимум функции.

По знаку производной можно судить о направлении изменения функции: если производная положительна, функция растет, если производная отрицательна, функция убывает. Если производная равна нулю, то функция не растет и не убывает. В случае нелинейной функции это означает, что в точке, где производная равна нулю, функция имеет минимум или максимум (математики часто говорят "экстремум" вместо "минимум или максимум"). (Рис.11.)

    

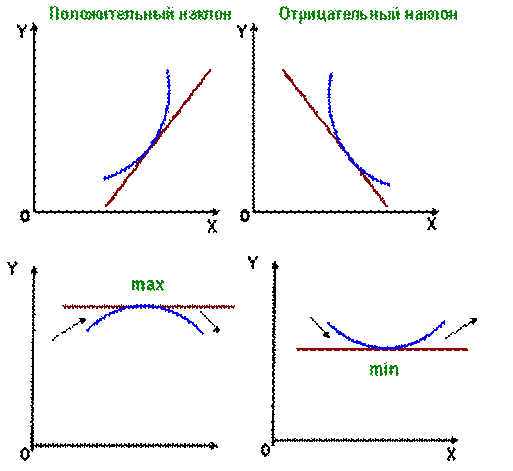
Точка x0 называется точкой минимума функции f, если для всех x из некоторой окрестности x0 выполняется неравенство f(x) ≥ f(x0.

 Это наглядно показано на рисунке 1:

Точка x0 называется точкой максимума функции f, если для всех x из некоторой окрестности x0 выполняется неравенство f(x) ≤ f(x0.

 Это наглядно показано на рисунке 2:

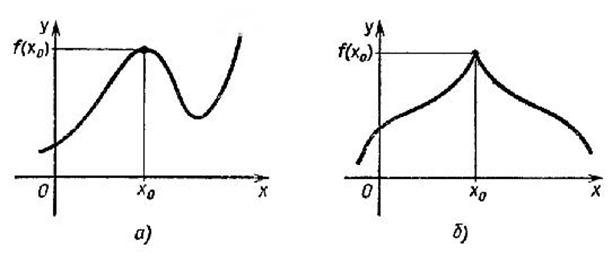
По определению значение функции f в точке x0 является наибольшим среди значений функции в окрестности этой точки, поэтому график функции в окрестности x0 имеет обычно либо вид гладкого холма, либо вид острого пика (рис. 1 а) и б) соответственно).

 В окрестности точки минимума графики изображаются в виде закругленной или острой впадины (рис. 2 а) и б) соответственно).

 Другие примеры поведения графиков функций в точках максимума и минимума приведены на рисунке ниже:

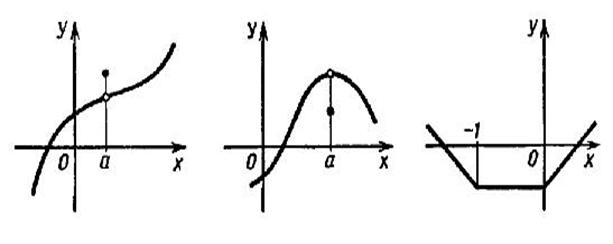
Слева направо: a - точка максимума; a - точка минимума; каждая точка из промежутка [-1; 0] является как точкой максимума, так и точкой минимума.

Для точек минимума и максимума функции есть общее определение - точки экстремума. Значение функции в этих точках соответственно назывется максимумом или минимумом этой функции. Общее название - экстремум функции. Точки максимума обычно обозначают xmax, а точки минимума - xmin.

Метод Лагранжа.

Метод множителей, метод решения задач на условный экстремум; Лагранжа метод множителей заключается в сведении этих задач к задачам на безусловный экстремум вспомогательной функции — т. е. функции Лагранжа.

Для задачи об экстремуме функции f (х1, x2,..., xn) при условиях (уравнениях связи) ji(x1, x2, ..., xn) = 0, i = 1, 2,..., m, функция Лагранжа имеет вид

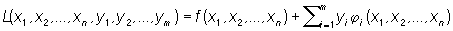
Множители y1, y2, ..., ym называются множителями Лагранжа.

Если величины x1, x2, ..., xn, y1, y2, ..., ym суть решения уравнений, определяющих стационарные точки функции Лагранжа, а именно, для дифференцируемых функций являются решениями системы уравнений

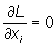, i = 1, …, n; 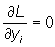, i = 1, …,m,

то при достаточно общих предположениях x1, x2, ..., xn доставляют экстремум функции f. Функция Лагранжа L применяется также при исследовании задач вариационного исчисления и математического программирования. Впервые Лагранжа метод множителей был предложен в 1797 Ж. Лагранжем в связи с задачами дифференциального исчисления.

Пример 1. Рассмотрим функцию:

F(X) = 3•x12+2•x22-3•x1+1

и условия-ограничения: x12 + x22 = 4

Перепишем ограничение задачи в неявном виде:

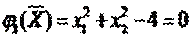
Составим вспомогательную функцию Лагранжа:

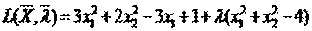
Необходимым условием экстремума функции Лагранжа является равенство

нулю ее частных производных по переменным хi и неопределенному

множителю λ.

Составим систему:

∂L/∂x1 = 2•x1•(λ+3)-3 = 0

∂L/∂x2 = 2•(λ+2)•x2 = 0

∂F/∂λ = x12+x22-4 = 0

Выражаем из первого уравнения x1:

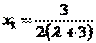
Из второго уравнения получаем x2 = 0.

Подставляем в третье уравнение:

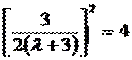    или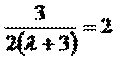     

Перепишем в виде: λ+3 =3/4 откуда λ=-9/4.

Подставляя λ в выражение для x1, получаем:

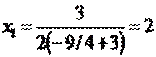
Стационарная точка (2;0). Значение функции в стационарной точке:

F(2;0) = 7.

Пример 2. Найдем точку экстремума функции:

F(X) = 2x12+x1x2+x22+2x1-4x2

Перепишем ограничение задачи в неявном виде:

φ1 = x1+x2-2 = 0

Составим вспомогательную функцию Лагранжа:

L = 2x12+x1x2+x22+2x1-4x2 + λ(x1+x2-2)

Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным хi и неопределенному множителю λ.

Составим систему:

∂L/∂x1 = 4x1+λ+x2+2 = 0

∂L/∂x2 = x1+λ+2x2-4 = 0

∂F/∂λ = x1+x2-2 = 0

Решаем данную систему с помощью формул Крамера.

Запишем систему в виде:

 

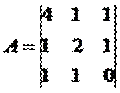
BT = (-2,4,2)

Главный определитель:

∆ = 4 • (2 • 0-1 • 1)-1 • (1 • 0-1 • 1)+1 • (1 • 1-2 • 1) = -4 = -4

Заменим 1-ый столбец матрицы А на вектор результата В.

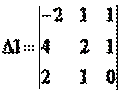
Найдем определитель полученной матрицы.

∆1 = -2 • (2 • 0-1 • 1)-4 • (1 • 0-1 • 1)+2 • (1 • 1-2 • 1) = 4

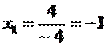
Заменим 2-ый столбец матрицы А на вектор результата В.

Найдем определитель полученной матрицы.

∆2 = 4 • (4 • 0-2 • 1)-1 • (-2 • 0-2 • 1)+1 • (-2 • 1-4 • 1) = -12

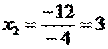
Заменим 3-ый столбец матрицы А на вектор результата В.

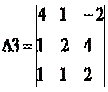
Найдем определитель полученной матрицы.

∆3 = 4 • (2 • 2-1 • 4)-1 • (1 • 2-1 • (-2))+1 • (1 • 4-2 • (-2)) = 4

Стационарная точка: F(-1; 3).

Исследование функции одной переменной.

Функция 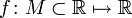 одной переменной является дифференцируемой в точке  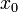своей области определения 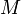, если существует такая константа 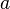, что для любой точки  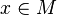 верно.

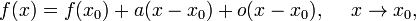
при этом число 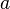 неизбежно равно производной

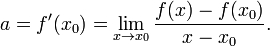
Функция одной переменной является дифференцируемой в точке 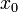 тогда и только тогда, она имеет производную в этой точке.

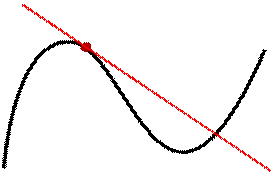
График функции 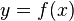   представляет собой кривую на плоскости 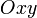, а график линейной функции 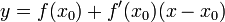, доставляет касательную прямую к этой кривой, проведённую в точке .

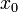Например, функция 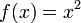 определена и дифференцируема в любой вещественной точке, поскольку её можно представить в виде .

При этом её производная есть 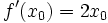, а уравнение касательной прямой, проведённой в точке 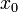,  имеет вид: .

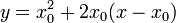Элементарные функции могут быть непрерывны в некоторой точке, но не быть в ней дифференцируемы.

Например, функция 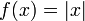 является непрерывной на всей вещественной оси, но её производная испытывает скачок при переходе через точку , в котором эта функция не является дифференцируемой. В этой точке нельзя провести и касательную к графику функции. Функция 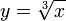 тоже непрерывна на всей вещественной оси и её график имеет касательные во всех точках, однако касательная, проведённая в точке , является вертикальной прямой и поэтому производная функции

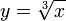 бесконечно велика в точке , а сама функция не дифференцируема в этой точке.

Примеры функции одной переменной.

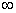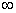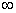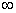Пример 1. у = х3. Эта функция задана на бесконечной прямой - < x < . Множество значений этой функции тоже бесконечная числовая прямая - < у < . Функция называется кубической параболой (рис. 3.1).

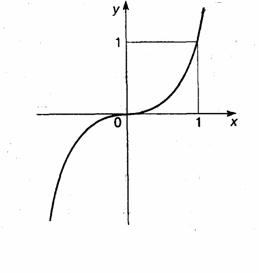рис. 3.1

Пример 2. у = 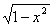. Функция задана на отрезке [—1, 1], множество ее значений — отрезок [0, 1]. Это половина окружности, лежащая в верхней полуплоскости (рис. 3.2).

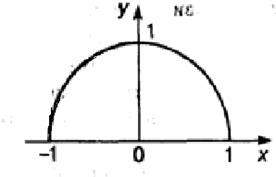
                                                            рис. 3.2

+1, если x > 0;

Пример 3. у = sign x = 0, если х = 0;

-1, если х < 0.

Термин sign происходит от латинского signum — знак. Функция задана на всем бесконечном промежутке ( - 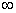,  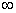) , а область ее значений состоит из трех чисел: —1, 0, 1 (рис. 3.3).

  рис. 3.3

Стрелки означают, что полупрямые не достигают точек ни оси ординат, так как при х = 0 значение функции определено по другому соответствию.

Список используемой литературы.

1.     Кудрявцев Л. Д., Математический анализ, т. 2, М., 1970.

2.     http://fislas.ru/lin_prog/veroatnoct5.htm

3.     Стефан Банах. Дифференциальное и интегральное исчисление. 1966 год. 437 стр.

4.     Ильин В.А., Садовничий В.А., Сендов Бл. Х. Математический анализ. Начальный курс. 2-е изд, перераб. 1985 год. 660 стр.

5.     И.А. Марон. Дифференциальное и интегральное исчисление в примерах и задачах (Функции одной переменной). 1970 год.