Метод градиентного спуска для решения систем нелинейных уравнений

МИНИСТЕРСТВО образованиЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

"Донской государственный технический университет"

ДГТУ

Кафедра "Программное обеспечение вычислительной техники и

автоматизированных систем"

Утверждаю

Зав. каф. «ПОВТ и АС»

Нейдорф Р. А.

«____»____________20    __ г.

Пояснительная записка

к курсовой работе по дисциплине

                      "Методы и системы компьютерной математики"

На тему: «Метод градиентного спуска для решения систем нелинейных уравнений»

       Студент          Кислица Артем Вячеславович

       Направление   231000.62 «Программная инженерия»

Руководитель работы                          Медведева Т.А.

            

Ростов–на–Дону

2014 г.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ........................................................................
........................... 4

1 ПОСТАНОВКА ЗАДАЧИ......................................................................... 5

2 ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.............................................................. 6

3 АЛГОРИТМИЧЕСКОЕ КОНСТРУИРОВАНИЕ..................................... 8

3.1 Формальное описание метода градиентного спуска....................... 8

4 ПРОГРАММНОЕ КОНСТРУИРОВАНИЕ............................................. 10

5 тЕСТИРОВАНИЕ ПРОГРАММЫ.......................................................... 12

6 ЗАКЛЮЧЕНИЕ......................................................................
.................. 19

7 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ................................ 20

ПРИЛОЖЕНИЕ а...............................................................................
........ 22

ВВЕДЕНИЕ

    При решении различных задач, встает вопрос о решении систем нелинейных уравнений. Системы нелинейных уравнений делятся на два вида, а  именно, алгебраические и трансцендентные. Без применения численных методов решить можно только малое количество нелинейных систем, лишь частные простые случаи.

В данной курсовой работе реализуется решение нелинейной системы уравнений методом градиентного спуска. Не смотря на то, что сам метод градиентного спуска является методом минимизации функции, существует возможность применения данного метода для систем нелинейных уравнений. Это является весьма полезно и способствует решению многих сложных практических задач.

1 ПОСТАНОВКА ЗАДАЧИ

    Целью данной работы является реализаций метода градиентного спуска для решения систем двух нелинейных уравнений.

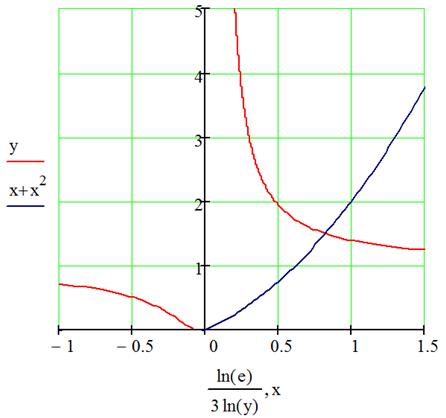
    При решении поставленной задачи необходимо сравнить полученные данные с данными, полученными стандартными способами решения, чтобы убедиться в правильности реализации метода. Для подбора начального приближения необходимо построить графики функций. Также необходимо вычислить абсолютную и относительную погрешности.

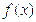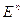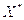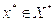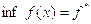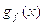2. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ. Пусть – выпуклая функция, определенная на евклидовом пространстве ,   – множество минимумов (оно может быть и пустым),  – точка минимума; ;  – субградиент функции 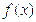 в точке  .

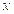Субградиент 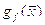 функции  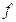в точке  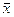есть вектор  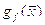такой, что

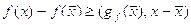 для всех .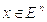

Из определения субградиента следует, что если 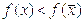, то

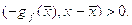                                                     (1)

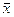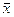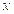Геометрически формула (1) означает, что антисубградиент в точке  образует острый угол с произвольным направлением, проведенным из  в сторону точки  с меньшим значением 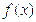. Отсюда, если  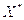непусто, 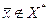, то при движении из 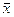 в направлении 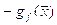 с достаточно малым шагом расстояние до 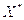 убывает. Этот простой факт лежит в основе субградиентного метода или метода обобщенного градиентного спуска (ОГС), впервые предложенного в [1] в связи с решением сетевой транспортной задачи.

Методом обобщенного градиентного спуска (ОГС) называется процедура построения минимизирующей последовательности 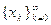, где 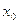 – начальное приближение, а 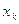 строятся по следующей рекуррентной формуле:

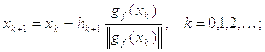                                             (2)

здесь 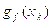  – произвольный субградиент функции 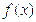 в точке 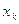,  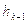– шаговый множитель. Если 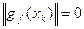, то 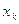 – есть точкой минимума функции 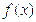 и процесс останавливается.

Для использования данного метода в системах уравнений (линейных и нелинейных)  требуется свести систему уравнений к одной функции. Представим данные преобразования в общем виде.

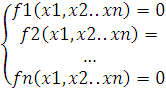
Тогда получаем функцию следующего вида

.

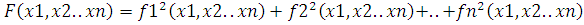Очевидно, что функция 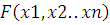 примет значение ноль тогда и только тогда, когда каждое слагаемое примет значение ноль. Также очевидно, что такое значение функции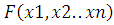 будет являться ее минимумом, а также решением системы уравнений.

Следовательно, можно применить методы минимизации для решения систем уравнений, предварительно преобразовав их, как показано выше.

3 АЛГОРИТМИЧЕСКОЕ КОНСТРУИРОВАНИЕ 3.1 Формальное описание метода градиентного спуска.

Ниже представлен в общем виде алгоритм метода градиентного спуска.

Входные данные x0,y0 – приближеннее значения, e – точность. F(x) – функций, к которой применяется алгоритм.

1.  Вычисление f0(x0,y0)

2.  Отыскание антиградиента 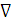Gx

3.  Отыскание антиградиента 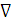Gy

4.  Задание начального шага h

5.  Пока не достигнута точность e выполнять цикл

5. 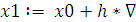 Gx

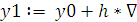6.  Gy

7. 

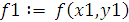
8.  Если 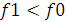 то

9.  

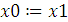
10.

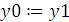
11.

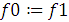
12. Вычисление погрешности

13. Иначе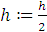

14. Вывод данных(х, у).

Как уже было сказано выше, данный метод является методом минимизации функции, и для того, чтобы было возможно данным методом решать системы нелинейных уравнений, над системой проводятся следующие манипуляции.

1.  Берутся квадраты функции системы

2.  Создается новая функция из суммы квадратов функций системы нелинейных уравнений.

3.  Полагается, что полученная функция может быть равна нулю тогда только тогда, когда квадрат каждой функции равен нулю, а следовательно минимизация такой функции даст решение нелинейной системы.

4 ПРОГРАММНОЕ КОНСТРУИРОВАНИЕ.

    Реализация метода градиентного спуска осуществлялась в среде MathCAD, так как данная среда удобна для проверки и тестирования, сравнения полученного результата с результатами полученными стандартными методами. Метод градиентного спуска представлен в виде программного модуля grad_sp исходный код которого представлен ниже.

    В программный модуль grad_sp в качестве входных параметров передаются следующие значения:

·     f – целевая функция;

·     x0, y0 – начальные приближения аргументов функции;

·     eps – точность;

где ,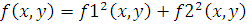

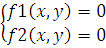
Для удобства сравнения продуктивности данного метода с иными, метод в качестве выходного параметра имеет матрицу А, где

Первый столбец – достигнутая точность.

Второй столбец – значение переменной .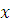

Третий столбец – значение переменной.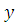

Четвертый столбец – значение .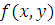

Данные в таблицу заносятся на каждой итерации, что позволяет наглядно и адекватно оценить результат работы метода

5 ТЕСТИРОВАНИЕ ПРОГРАММЫ.

    Работоспособность разработанного модуля была проверена на примерах трех систем нелинейных уравнений.

1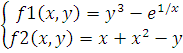

2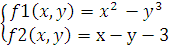

3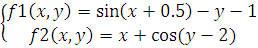

 Для каждой системы уравнений имеются график, сводные таблицы результатов работы модуля и данные – полученные при решении стандартными средствами MathCAD. Также, каждая система была решена методом Ньютона(программный модуль представлен в приложении А), что позволяет сравнить работоспособность и увидеть преимущества и недостатки метода градиентного спуска. 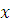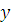Выходным параметром, также является таблица, в которой: первый столбец – номер итерации; второй – значение ; третий – значение ; четвертый – достигнутая точность.

Тестовый пример №1.

Рисунок 1 – таблица результатов работы модуля.

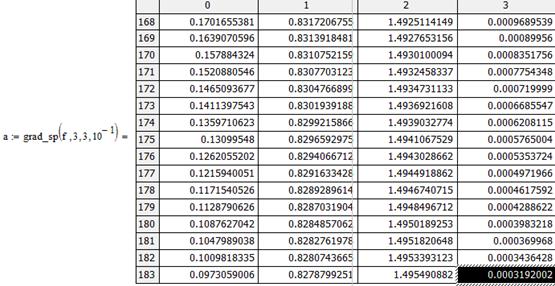
Далее представлено решение этой же системы методом ньютона

Рисунок 2 – результат работы метода Ньютона.

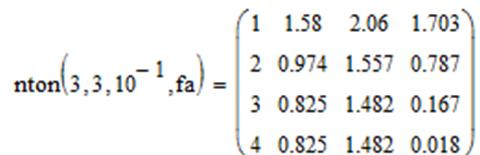
Ниже представлены данные погрешности и данные решения стандартными средствами MathCAD, а также график системы.

Рисунок 3 – данные погрешностей и решения стандартными средствами MathCad

 

Рисунок 4 – график системы нелинейных уравнений.

 

Тестовый пример №2.

	Рисунок 5 – таблица результатов работы модуля.

 

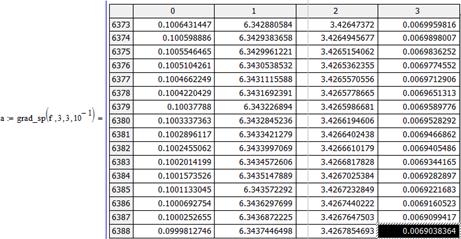
Далее представлено решение этой же системы методом ньютона

Рисунок 6 – результат работы метода Ньютона.

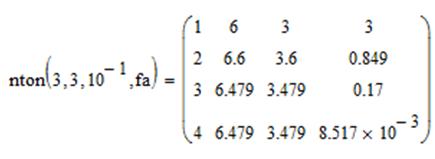
Ниже представлены данные погрешности и данные решения стандартными средствами MathCad, а также график системы.

Рисунок 7 – данные погрешностей и решения стандартными средствами MathCad

 

Рисунок 8 – график системы нелинейных уравнений.

 

Тестовый пример №3.

	Рисунок 9 – таблица результатов работы модуля.

 

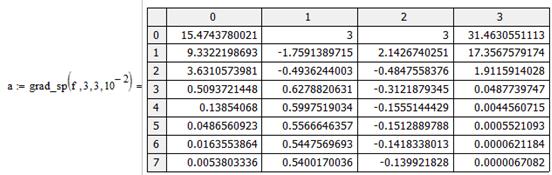
Далее представлено решение этой же системы методом Ньютона.

Рисунок 10 – результат работы метода Ньютона.

 

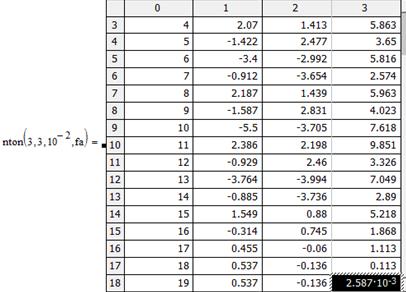
Ниже представлены данные погрешности и данные решения стандартными средствами MathCAD, а также график системы.

Рисунок 11 – данные погрешностей и решения стандартными средствами MathCad

 

Рисунок 12 – график системы нелинейных уравнений.

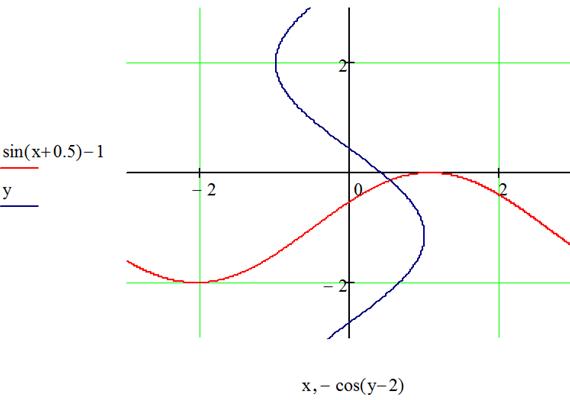
Таким образом, из представленных выше данных видно, что метод градиентного спуска получается очень трудоемким, требуется большое количество итераций для достижения необходимой точности. Если сравнивать данный метод с методом Ньютона, то видно, что метод Ньютона намного эффективнее. Можно с уверенностью сказать, что метод градиентного спуска для решения системы нелинейных уравнений работает и выдает точные данные с погрешностью установленной пользователем, что прекрасно видно из данных представленных выше.

5 ЗАКЛЮЧЕНИЕ

    В ходе проделанной работы был реализован метод градиентного спуска для решения систем нелинейных уравнений. Разработанный метод был проверен на работоспособность. После получения конечных результатов была проведена их проверка путем сравнения с достоверными данными полученными стандартными средствами, а также с данными, полученными решением системы методом Ньютона. Было установлено, что метод градиентного спуска в частных случаях превосходит метод Ньютона, как в примере 3. Но в целом, метод является весьма трудоемким, и требует достаточно большого количества итераций, на порядки превосходящего количество итераций в других методах.

6. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.

·     Блатов И.А., Старожилова О.В.  «КОНСПЕКТ ЛЕКЦИЙ ПО УЧЕБНОЙ ДИСЦИПЛИНЕ Вычислительная математика», Самара, 2010.

·     Поршнев С. В., Беленкова И. В. «Численные методы на базе MathCad». Феникс, 2005.

·     Электронная энциклопедия «Википедия». Url:-[ http://ru.wikipedia.org/wiki/Метод градиентного спуска.

Приложение А.

Программный модуль реализации метода Ньютона.

Входные данные:

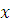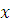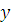 - начальное приближение переменной ;

 - начальное приближение переменной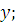

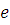 - точность;

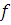 - вектор функций.

Выходные данные:

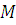 - матрица данных, где

·        первый столбец – номер итерации;

·         второй столбец – значение ;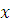

·        третий столбец – значение ;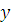

·        четвертый столбец – достигнутая точность.