Курсовая Работа 

 

 

по дисциплине «Теории электрической связи»

Тема: Квазиоптимальная по критерию минимума вероятности

ошибки система связи

Принял: Старший преподаватель А.Т. Омаров «__»___________2016 Выполнила:

                                    АСТАНА 2016

Содержание

Введение 1 Задание к курсовой работе 1.1 Структурная схема системы связи 1.2 Преобразование аналогового сигнала в цифровой 1.3 Кодирование кодом с проверкой на четность 1.4 Характеристики источника двоичных сообщений 1.5 Структурная схема цифрового модулятора 1.6 Структурная схема цифрового демодулятора 1.7 Определение h 1.8 Вероятность ошибочного приема кодовой комбинации PОШ.К.К. 1.9 Пропускная способность канала связи Заключение Список литературы

3 4 6 10 13 15 17 19 21 22 23 24 25

Введение

Современные системы связи представляют собой сложные комплексы, состоящие из различных функционально зависимых элементов. В общем случае эффективность любой технической системы определяется количеством и качеством выдаваемой продукции. В системах связи таким продуктом является передаваемая информация, количество которой определяется средней скоростью передачи бит/с, а качество - величиной ошибки. Важнейшим показателем эффективности систем связи является информационная эффективность, определяющая степень использования системой пропускной способности канала, а также энергетическая и частотная эффективности, характеризующие использование канала по мощности и по частоте. Зависимость между этими показателями носит обменный характер (увеличение одного показателя связано с уменьшением другого и наоборот) и зависит от способов модуляции и кодирования.

Задача оптимизации систем передачи информации сводится к нахождению наилучшего варианта системы при заданных условиях и ограничениях, при котором потребителю в единицу времени доставляется максимальное количество информации при заданной верности передачи. Для повышения эффективности систем используются сокращение избыточности источника, помехоустойчивое кодирование и др.

В курсовой работе рассматривается построение квазиоптимальной по критерию минимума вероятности ошибки системы связи при заданных виде модуляции и способе приема и сравнение ее параметров с потенциально возможными (предел Шеннона).

1 ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ

Разработать квазиоптимальную по критерию минимума вероятности ошибки систему связи, рассчитать ее основные параметры и указать пути совершенствования разработанной системы связи.

Необходимо:

1.1 Сделать сравнительный анализ потенциальной помехоустойчивости и области применения заданного вида дискретной (цифровой) модуляции в сравнении с другими видами модуляции. Пояснить, в каналах какого типа являются оптимальными по критерию минимума вероятности ошибки заданный вид модуляции и способ приема.

Составить структурную схему системы связи для заданного вида модуляции и способа приема (таблица 1).

1.2 Предполагая, что передаваемый информационный сигнал является низкочастотным аналоговым сигналом, описать преобразования, которым он подвергается в АЦП при переходе к первичному цифровому сигналу ИКМ.

Рассчитать частоту дискретизации F_д и интервал дискретизации Т_д цифрового ИКМ сигнала, если ширина спектра аналогового сигнала - 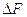 (таблица 2).

Составить кодовые комбинации заданных от счетов и нарисовать временную диаграмму цифрового ИКМ сигнала. Число уровней квантования – M (таблица 2), квантование равномерное, шаг квантования - 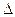 (таблица 3), код – двоичный симметричный.

1.3 Пояснить процесс помехоустойчивого кодирования кодом проверки на четность и закодировать полученные выше кодовые комбинации этим кодом.

Нарисовать структурную схему кодера и временную диаграмму цифрового сигнала с учетом применения этого кода.

Рассчитать тактовую частоту F_maкm и тактовый интервал Т_такт (длительность единичного элемента кодовой комбинации) цифрового ИКМ сигнала, закодированного кодом проверки на четность.

1.4 Определить параметры источника сообщений (методические указания к данному пункту) при вероятности появления в цифровом ИКМ сигнале элемента (символа) «1», равном p(1)=0,001+0,kn, где k, n - предпоследняя и последняя цифры номера варианта.

Найти количество информации в кодовых комбинациях от счетов I_к.к.1 и I_к.к.2.

Рассчитать скорости модуляции В и передачи информации R для N-канальной (таблица 3) цифровой системы передачи.

1.5 Составить структурную схему дискретного (цифрового) модулятора системы связи и записать алгоритм его работы.

Нарисовать временные диаграммы цифрового информационного сигнала на входе модулятора и модулированною сигнала на выходе модулятора, а также временные диаграммы сигнала в характерных точках схемы модулятора.

Рассчитать ширину спектра модулированного сигнала и нарисовать его спектральную диаграмму.

1.6 Составить структурную схему демодулятора (приемника) системы связи, для заданного способа приема (таблица 1) и записать алгоритм его работы.

Нарисовать временные диаграммы модулированного сигнала на входе демодулятора и демодулированного информационного сигнала на выходе демодулятора, а также временные диаграммы сигнала в характерных точках схемы демодулятора.

1.7 Определить величину параметра h² на входе демодулятора, при которой достигается заданная вероятность ошибки р_ош (таблица 4), если единственной помехой, воздействующей на сигнал, считать аддитивный белый гауссовский шум со спектральной плотностью мощности W₀ (таблица 4).

Рассчитать амплитуду модулированного сигнала, при которой достигается полученное значение h².

1.8 Найти вероятности ошибочного приема кодовой комбинации Р_oш.к.к без учета и с учетом помехоустойчивого кодирования кодом проверки на четность.

1.9 Определить пропускную способность канала заданной системы связи.

Рассчитать потенциально возможную пропускную способность канала при увеличении полосы частот канала 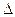F_K до бесконечности (предел Шеннона).

1.10 Сделать заключение по результатам работы:

§  сравнить вероятности ошибочного приема кодовых комбинаций (пункт 3.8) и сделать заключение об эффективности помехоустойчивого кодирования кодом проверки на четность;

§  сравнить пропускную способность канала с производительностью источника сообщений и сделать заключение о возможности повышения пропускной способности канала, способах ее повышения;

§  сравнить заданную вероятность ошибки с вероятностью ошибки, которая может быть получена в соответствии с теоремой кодирования Шеннона и сделать заключение о возможности повышения верности передачи, способах ее повышения;

§  сравнить пропускную способность системы связи с потенциальной ее возможностью (пределом Шеннона) и сделать заключение об эффективности использования пропускной способности канала для заданного вида модуляции и способа приема.

Исходные данные:

Номер варианта - 23

Вид модуляции – ЦАМ

Способ приема – неоптимальный

Ширина спектра аналогового сигнала - ∆F = 3,4кГц

Число уровней квантования – M= 256

Шаг квантования - 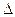 = 1,6 мВ

N = 6

Вероятность ошибки - Р_ош = 2∙10^-6

Спектральная плотность мощности шума - W₀=2∙10^-6 В²/Гц.

1.1  Структурная схема системы связи

Под потенциальной помехоустойчивостью понимают предельно достижимую помехоустойчивость при заданных сигналах и видах помех. Ее нельзя превысить никакими способами обработки сигналов при существующей помехе в заданной системе связи.

Приемник, обеспечивающий максимальную (потенциальную) помехоустойчивость приема, называют оптимальным.

Помехоустойчивость приема дискретных сигналов оценивается вероятностью ошибки при приеме заданных сигналов. Она зависит от вида модуляции и от способа приема. Для передачи дискретных сигналов используют дискретную амплитудную (ДАМ), частотную (ДЧМ), фазовую (ДФМ), относительную фазовую (ДОФМ) модуляции. Наибольшую потенциальную помехоустойчивость (минимально возможную вероятность ошибки) дает система с ДФМ, затем идут системы с ДОФМ, ДЧМ, ДАМ.

На рисунке 1 приведены векторные диаграммы сигналов дискретной модуляции.

ДФМ	ДЧМ	ДАМ
S0(t)    U          U    S1(t)                 0           ∆S = 2U	S0(t)       U          ∆S =         0     U       S1(t)	S0(t)    U       S1(t)   0             ∆S = U

Рисунок 1- Векторные диаграммы сигналов дискретной модуляции.

ДФМ сигналы S₁(t) и S₀(t), служащие для передачи по каналу символов «1» и «0» кодовых комбинаций двоичного кода, из которых состоит дискретное сообщение, являются противоположными, т.е. S₁(t) = - S₀(t). Разность между этими сигналами (расстояние между концами векторов сигналов) ∆S = 2U, где U - амплитуда сигналов. ДЧМ сигналы S₁(t) и S₀(t)- ортогональные сигналы. Для них ∆S = 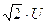. Для ДАМ сигналов - ∆S = U.

Таким образом, наиболее отличаются друг от друга сигналы S₁(t) и S₀(t) при ДФМ, что улучшает их распознаваемость, т.е. уменьшает вероятность ошибочного приема. Наименее отличаются друг от друга сигналы S₁(t) и S₀(t) при ДАМ, что обуславливает наименьшую помехоустойчивость этого вида модуляции. Использование ДФМ дает энергетический выигрыш по сравнению с ДЧМ в 2 раза (на З дБм), а по сравнению с ДАМ- в 4 раза (на 6 дБм). ДОФМ использует преимущества ДФМ. Она менее помехоустойчива чем ДФМ и более помехоустойчива, чем ДАМ. По сравнению с ДЧМ ДОФМ более помехоустойчива при малых помехах и менее помехоустойчива при сильных помехах.

ДОФМ используется при необходимости обеспечить высокую помехоустойчивость в каналах с невысоким уровнем помех, где ДЧМ и ДАМ дают меньшую помехоустойчивость. Чаще ДОФМ используется в проводных каналах при высокой скорости передачи и в радиоканалах с невысоким уровнем помех.

Существуют два способа приема:

- когерентный, где при демодуляции используется информация о фазе принимаемого сигнала и требуется согласованность по фазе (когерентность) между принимаемым и опорным сигналами; решение о принимаемом сигнале выносится по мгновенным значениям напряжения сигнала;

- некогерентный, где сведения о фазе сигнала не используются, а решение о принимаемом сигнале выносится по значениям его огибающей.

Эти способы приема могут использоваться для любых видов модуляции. Когерентные методы приема требуют значительного усложнения схем приемника для оценки фазы принимаемого сигнала, поэтому здесь целесообразно использовать ДФМ, дающую наибольшую помехоустойчивость, а некогерентный прием лучше совмещать с ДАМ и ДЧМ, что дает преимущество в простоте схем приемников и в менее жестких требованиях к стабильности частоты сигнала.

В каналах различного типа есть ограничения на вид модуляции и способ приема. В каналах с быстрыми флуктуациями фазы и частоты неэффективно использовать ДФМ и ДЧМ, так как это приводит к значительному усложнению схемы приемника, что не окупается достигнутым при этом увеличением помехоустойчивости. Систему с ДФМ нельзя использовать при некогерентном приеме, т.к. при ДФМ информация заложена в фазу сигналов, а при неизвестной фазе сигналов они неразличимы друг от друга.

В каналах с неопределенной фазой сигнала на приеме приходится  отказываться от применения когерентного метода приема даже в тех случаях, когда с помощью сложных устройств можно оценить начальную фазу принимаемого сигнала. При этом используют алгоритм приема построенный в предположении, что начальная фаза принимаемого сигнала неизвестна - т.е. некогерентный способ приема.

Однако, в каналах с медленными флуктуациями фазы, путем ее оценки, можно достаточно надежно предсказать ее на интервале анализа. При этом, можно реализовать оптимальный когерентный прием, так как фаза изменяется достаточно медленно и разности фаз между соседними единичными элементами практически сохраняются. Здесь вполне возможен когерентный прием с применением ДОФМ. То же и с ДЧМ в каналах с медленными флуктуациями частоты.

Оптимальный когерентный прием ОФМ сигналов является оптимальным для каналов с медленным флуктуациями фазы при требовании высокой помехоустойчивости приема.

Структурная схема системы связи приведена на рисунке 2.

ИС - источник непрерывных сообщений b.

Сообщ/сигн.- преобразователь непрерывных сообщений b в аналоговый первичный сигнал U_a(t).

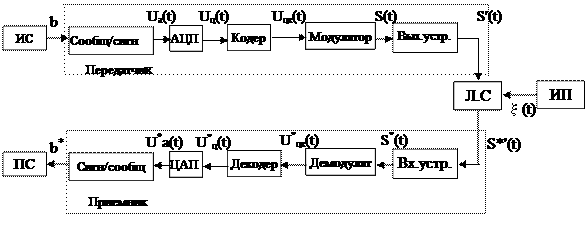Рисунок 2- Структурная схема системы связи

АЦП - аналого-цифровой преобразователь, преобразующий аналоговый первичный сигнал U_a(t) в цифровой сигнал U_ц(t).

Кодер - для кодирования кодовых комбинаций простого кода цифрового сигнала помехоустойчивым кодом с проверкой на четность.

Модулятор - для преобразования первичного цифрового сигнала U_цк(t) во вторичный высокочастотный сигнал S(t), соответствующий параметрам линии связи. Это дискретный относительный фазовый модулятор, в котором информация, переносимая

первичным цифровым сигналом, вкладывается в разность фаз сигналов на соседних единичных интервалах, путем изменения ее по закону первичного информационного (модулирующего) цифрового сигнала.

Вых. устр. - выходное устройство, включающее в большинстве случаев усилитель, полосовой фильтр, ограничивающий спектр сигнала для уменьшения помех взаимного влияния в различных каналах, согласующее устройство передатчика с линией связи.

Л.С. - линия связи - физическая среда для передачи сигнала.

ИП- источник помех x(t), вызывающих отклонение принятых сигналов от переданных (включая искажение сигнала). S^*¢(t) = S¢(t) +x(t).

Вх.устр. - входное устройство, производящее фильтрацию входного сигнала для уменьшения уровня помех на входе демодулятора, усиление сигнала и согласование приемника с линией связи.

Демодулят. – демодулятор, служащий для обратного преобразования вторичного ВЧ сигнала S^*(t) в первичный цифровой НЧ сигнал U^*_цк(t), несущий информацию. Это дискретный относительный фазовый демодулятор, в котором информационный цифровой сигнал выделяется из изменения разности фаз сигналов на соседних единичных интервалах.

Декодер - декодирует кодовые комбинации помехоустойчивого кода, обнаруживая в ней ошибки. Код с проверкой на четность обнаруживает все ошибки нечетной кратности.

ЦАП - цифро-аналоговый преобразователь, преобразует цифровой сигнал U^*_ц(t) в первичный аналоговый сигнал U^*_a(t).

Сигн/сообщ. - преобразователь аналогового первичного сигнала U^*_a(t) в непрерывное сообщение b^*.

ПС - получатель непрерывных сообщений.

1.2  Преобразование аналогового сигнала в цифровой

Для преобразования аналогового сигнала в цифровой ИКМ сигнал, в АЦП осуществляются последовательно три операции. Структурная схема АЦП приведена на рисунке 3.

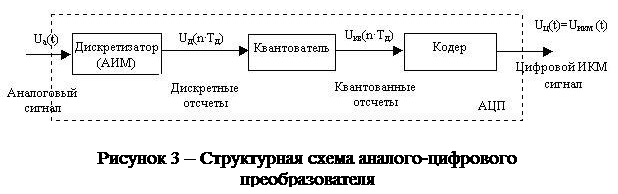
Описание преобразований аналогового сигнала в цифровой в АЦП нужно проиллюстрировать конкретным примером для двух заданных отсчетов сигнала со значениями, равными номеру варианта с положительным знаком и половине номера варианта с отрицательным знаком в условных единицах.

Определим значения дискретных отсчетов сигнала:

F_д≥2∙F_ж; (Т_д£),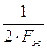                                                                                 

где первый дополнительный элемент служит для кодирования знака номера уровня (полярности кодируемого отсчета), обычно 0-для отрицательных и 1-для положительных значений.

Определим квантованные (разрешенные) значения отсчетов, следующие от нуля в положительную и отрицательную сторону через шаг квантования.

Составим нумерацию всех уровней квантования, начиная от нулевого в положительную и отрицательную стороны.

Заданные отсчеты квантуем, то есть их значения приравниваем к ближайшим квантованным (разрешенным) значениям.

Составляем кодовые комбинации, соответствующие номерам уровней для k=11.

На месте разрядов, которые участвовали в сумме, ставится элемент «1», а на месте разрядов, не участвовавших в сумме – элемент «0». Первый (знаковый) элемент для отрицательного числа – «0». Для положительного – «1».

k≥1+log₂М,                                                                                                    
             

Решения:

F_в=3,4 кГц, F_д>2∙F_в=2∙3,4=6,8 кГц. F_д=6,8 кГц.

Т_д=1/F_д=1/(6,8∙10³)=142∙10^-6 с=142 мкс.

М=256; k≥1+log₂ М=1+log₂256=9 элемент.

Квантование шага D=1,6 мВ.

АЦП- Во входе Диапазон смыслов аналогтық сигнала:

[-D∙(М-1)¸D∙(М-1)]=-408¸408 мВ.

АЦП -  Технические параметры НА 1- таблице.

Составляем таблицу:

1-    Таблица 1.

UKB, у.е.	0	±1,6	...	±9,6	±11,2
NУР.	0	±1	...	±6	±7
Кодовая комб-я	100000000	100000001 000000001	...	100000110 000000110	100000111   000000111
Uкв, мВ	±20,8	±22,4	…	±406,4	±408
N	±13	±14	…	±254	±255
Кодовая комб-я	100001101 000001101	100001110 000001110	…	111111110 011111110	111111111 011111111

Дискретность смыслов учет: U_д1=N_{вариант}= 23 мВ.

                                                          U_д2=- U_д1/2=-23/2=-11,5 мВ.

Совпадания в учета номера квантование уровней:

                                                           N₁=U_д1/D=23/1,6=14,4. N₁=14.

                                                           N₂=U_д2/D=-11,5/1,6=-7,2. N₂=-7.

Квантование смысл:                       U_кв1=N₁·D=14·1,6=22,4мВ.

                                                            U_кв2=N₂·D=-7·1,6=-11,2 мВ.

   Кодовые комбинации учет: Q₁(0,1)= 100001110

                              Q₂(0,1)= 000000111

Квантование ошибок: h=U_д-U_кв. h₁=23-22,4=0,6 мВ;

                                                                     h₂=-11,5-(-11,2)=0,3 мВ.

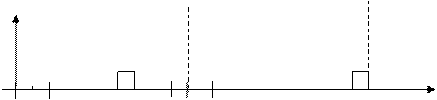                       u_ц(t)     1- кодовая                 2- кодовая

                                 комбинация                     комбинация

                  1  0  0  0  1 0  1  0  0  1 0   0  0  0  0  1 0 1  0  1                 

                                                          

                                                                                                                t, мкс                             

                 0                                   142                             284                        

Рисунок 4 – Временная диаграмма цифрового ИКМ сигнала на выходе АЦП

1.3  Кодирование кодом с проверкой на честность

При кодировании помехоустойчивым (корректирующим) кодом с проверкой на четность, который позволяет обнаружить все ошибки нечетной кратности, к информационной кодовой комбинации длиной k элементов добавляется один проверочный элемент - r, доводящий число единиц в полной кодовой комбинации до четного числа. Проверочный элемент ставится в конце кодовой комбинации после информационных элементов. Длина кодовой комбинации кода с проверкой на четность равна:

                                                           

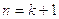
где k - длина кодовой комбинации простого кода.

Проверочный элемент определяется суммой по модулю два всех информационных элементов кодовой комбинации простого кода:

                                               

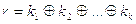
где Å - сумма по модулю два;

k₁, k₂, … k_к - элементы кодовой комбинации простого кода.

Параметры кода: (k, k+1). k=9 эл.; r=1 эл.; n=9+1=10 эл.,

Для простого кода, параметры кода с проверкой на четность: (12,11).

Для кодовой комбинации Q₁(0,1) = 100001110,

r=1Å0Å0Å0Å0Å1Å1Å1Å0=0

Полная кодовая комбинация кода с проверкой на четность:

 F₁(0,1)= 1000011100.

Для кодовой комбинации Q₂(0,1) =000000111,

r=0Å0Å0Å0Å0Å0Å1Å1Å1=1

Полная кодовая комбинация кода с проверкой на четность: F₂(0,1)=0000001111.

Структурная схема кодера кода с проверкой на четность показана на рисунке 5.

                           k₁  k₂     k₃    k₄     k₅    k₆    k₇  k₈  k₉   k₁₀   

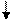
                                                                                                             RG1

1

2

3

4

5

6

7

8

9

10

Å

                                                                                
                

                                                                                
               

 

                                                                                                                            

                                                                                
      

 

1

2

3

4

5

6

7

8

9

10

11

                                k₁   k₂    k₃    k₄     k₅   k₆    k₇   k₈   k₉   k₁₀         r    RG2

Рисунок 5 – Структурная схема кодера кода с проверкой на четность (11,10)

Временная диаграмма цифрового сигнала с учетом кодирования кодом с проверкой на четность приведена на рисунке 6.

     U_цк(t)           1- Кодовая комб-я               2- Кодовая комб-я

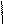
     1  0  0  0  1  0  1  0  0   1  0  0  0  0  0   0  1  0  1  0  1  1       

                         

                                                                                                      t, мкс

  0                                              142                                                 284    

Рисунок 6 - Временная диаграмма цифрового сигнала на выходе кодера кода с проверкой на четность (12,10)

1.4 Характеристики источника двоичных сообщений

Под производительностью источника понимают среднее количество информации, выдаваемое источником в единицу времени (за 1 сек.) - Н".

Н" =Н_эл/Т_такт, или Н" = Н_эл∙F_такт, бит/с.                   

где Н_эл – энтропия единичного элемента (среднее количество информации содержащееся в одном элементе), бит/эл; Т_такт.- – длительность единичного элемента (тактовый интервал), с.

Единичный элемент кодовой комбинации передается за тактовый интервал.

Для источника независимых двоичных сообщений:

Н_эл  = - [р(1)×log₂ р(1) + р(0)×log₂ р(0)], бит/эл,                 

где р(1) и р(0) - вероятности появления символов «1» и «0».

Так как появление символов «1» и «0» составляют полную группу событий, то:

                          р(1)+р(0) = 1, отсюда р(0) = 1-р(1)

F_такт=F_д∙n и Т_такт=1/F_такт, и Т_такт=Т_д/n и F_такт=1/Т_такт.          

Решения:

F_д=7 кГц; n=10 эл.

F_такт=F_д∙n=7∙10³∙10=70∙10³ Гц=70кГц;

Т_такт=1/F_такт=1/(70∙10³)=14∙10^-6 с=14 мкс.

 

1.5 СТРУКТУРНАЯ СХЕМА ЦИФРОВОГО МОДУЛЯТОРА

 

Рисунок 7- Структурная схема цифрового амплитудного модулятора.

Г_н - генератор несущего сигнала S_н(t) = U× cosw_нt;

´ - перемножитель сигналов.

Алгоритм работы цифрового амплитудного модулятора приведен в таблице 2.

     Таблица 2

Символ	Первичный информационный сигнал Uцк(t) на входе модулятора	Вторичный модулированный сигнал S(t) на выходе модулятора
0	U0(t) = 0	S0(t) = 0
1	U1(t) = Uимп	S1(t) = Sн(t) = U× coswнt

Временные диаграммы сигналов в различных точках схемы модулятора показаны на рисунке 8.

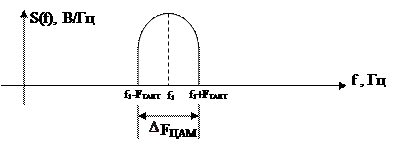
Спектральная диаграмма ЦАМ сигнала приведена на рисунке 9.

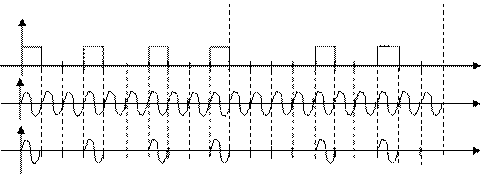                                                    1-я  кодовая                                   2-я  кодовая

                                                     комбинация                                  комбинация

             U_цк(t)    1   0   0    1   0   0    1   0   0   1   0    0   0   0   1   0    0   1    0   0

    1)              

                     0                                                                                         
                        t, мкс

    2)

                   0                                                                                                                    t, мкс

    3)     S(t)                                                                                                                          t, мкс

                     0                                                                                                                

                                                                         125                                             250    

Рисунок 8- Временные диаграммы сигналов в различных точках схемы модулятора

 

                         0 

Рисунок 9- Спектральная диаграмма ЦАМ сигнала.

Ширина спектра ЦАМ сигнала зависит от ширины спектра прямоугольного видеоимпульса (модулирующего сигнала), определяемого длительностью видеоимпульса Т_такт. Ширина спектра амплитудно-модулированного сигнала определяется по упрощенной формуле: 

DF_ЦАМ = 2/Т_такт., Гц,  или  DF_ЦАМ = 2×F_такт. , Гц.

DF_ЦАМ = 2×70×10³=140кГц.

 

1.6 Структурная схема цифрового демодулятора

СТРУКТУРНАЯ СХЕМА ЦИФРОВОГО ДЕМОДУЛЯТОРА

Структурная схема цифрового демодулятора при неоптимальном приеме ЦАМ сигналов приведена на рисунке 10.

 

Рисунок 10- Структурная схема неоптимального приемника ЦАМ сигналов.

Z(t)=S*(t)=S(t)+x(t) - принятый сигнал, представляющий собой смесь переданного сиг-нала S(t) и помехи x(t);

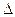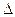ПФ- полосовой фильтр с эффективной полосой пропускания F_Э=F_ЦАМ;

АД- амплитудный детектор (детектор огибающей), выделяет огибающую принятого сигнала;

ФНЧ- фильтр нижних частот, совместно с АД выделяет огибающую сигнала;

РУ- решающее устройство, в котором, напряжение U с выхода ФНЧ в определенные моменты времени (в середине единичного элемента) сравнивается с пороговым напряжением- U_пор и, в зависимости от результата сравнения, формируются первичные сигналы U*_цк(t): U*₁(t),  либо U*₀(t).

Алгоритм работы демодулятора приведен в таблице 3.

Таблица 3.

Принимаемый сигнал S*(t) на входе демодулятора	Первичный информационный сигнал U*цк(t) на выходе демодулятора
S*1(t)= S*н(t)=U×coswнt+x(t)	U*1(t)=Uимп - символ «1»
S*0(t)=0+x(t)	U*0(t)=0 - символ «0»

Временные диаграммы сигналов в разных точках схемы демодулятора показаны на рисунке 11.

                 S^*(t)

    1) 

                     0                                                                                 
                            t, мкс

    2)

                       0                                                                                                          t, мкс

    3)

 0                                                                              
                           t, мкс

                                 1   0   0   1  0   0   1   0   0  1   0   0  0   0    1   0   0   1   0   0

    4)     U^*цк(t)

                                                                                        
                                              t, мкс

                        0                                             125                                           250 

                                  1-я кодовая комбинация         2-я кодовая комбинация                            

Рисунок 11- Временные диаграммы сигналов в различных точках схемы демодулятора.

1.7 Определение h параметр.

ОПРЕДЕЛЕНИЕ АМПЛИТУДЫ СИГНАЛА

 

Вероятность ошибки при неоптимальном приеме сигналов с ЦАМ в канале с "белым" Гауссовским шумом в теории потенциальной помехоустойчивости не определена точной формулой.

Вероятность ошибки в неоптимальном фильтровом демодуляторе ЦАМ сигналов больше, чем при некогерентном оптимальном приеме. Это ухудшение помехоустойчивости вызывается двумя основными факторами:

-          уменьшением отношения сигнал/помеха по сравнению с согласованными фильтрами (корреляторами);

-          межсимвольными помехами, вызываемыми переходными процессами в фильтрах (остаточными колебаниями, возникающими в результате воздействия предыдущих элементов сигнала).

Переход от оптимального к неоптимальному приему эквивалентен энергетическому проигрышу в d=F_Э×T_с =В раз, где В- база сигнала; F_Э- эффективная полоса пропускания фильтра на входе приемника; T_с – длительность сигнала.

Так как полоса частот канала равна ширине спектра сигнала на выходе модулятора, то 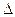F_Э=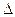F_ЦАМ=2×F_такт. Т_с=Т_такт=1/F_такт. d=2, то есть для получения одинаковой вероятности ошибки в схеме с полосовым фильтром, требуется в 2 раза большая мощность сигнала, чем в оптимальном некогерентном приемнике (энергетические потери на 3 дБ). Вероятность ошибки при оптимальном некогерентном приеме ЦАМ сигналов рассчитывается по формуле:  

р_ош=0,5∙exp(- h²/4)

где  h²=E/Wo; E- энергия сигнала S₁(t), В²∙с;  Wo- спектральная плотность мощности помехи В²∙с.

Тогда для неоптимального приема сигналов с ЦАМ: р_ош=0,5∙exp(- h²/8)

Отсюда h²= - 4∙ln(2∙р_ош);

h²= - 4∙ln(2∙2∙10^-6)

Мощность гармонического несущего сигнала Р_с=U ²_m/2, В², где U_m-амплитуда сигнала, B

Энергия сигнала E=P_c∙T_такт=P_c/F_такт, В²∙с;  E=h²∙Wo, В²∙с.

Тогда после подстановки и преобразования получим:

U=Ö2∙h²∙Wo/T_такт, В или U=Ö2∙h²∙Wo∙F_такт, В

U==Ö2∙50∙2∙10 ^-6 ∙70∙10^-3   =3,74В

  1.8 Вероятность ошибочного приема кодовой комбинации Р_{ош к к.}

Помехоустойчивый код с проверкой на четность позволяет обнаруживать все ошибки нечетной кратности. Кодовая комбинация, содержащая ошибки, будет декодирована неверно, если в ней будет четное число ошибочных элементов. Так как Р_ош << 1, то можно учитывать только вероятность ошибочного приема двух элементов кодовой комбинации. Тогда вероятность неверного декодирования n-элементной кодовой комбинации равна:

Р_ош.к.к.=1-P(0,k)=1-(1-p_ош.)^k,    

    

 Р_{ош.к к}=P(2,n)+P(4,n)+…=C²_n∙p²_ош∙(1-p_ош)^n-2+C⁴_n∙p⁴_ош∙(1- p_ош)^n-4+…,    

                                              

С²_n - число сочетаний из n элементов по 2 элемента (показывает число возможных вариантов двукратной ошибки в n элементной кодовой комбинации кода);

n - длина кодовой комбинации помехоустойчивого кода.      

C^t_n=n!/[t!(n-t)!].

Р_{ош к к.}≈P(2,n)=C²_n∙p²_ош∙(1-p_ош)^n-2≈C²_n∙p²_ош                                                     

Р_ош=2∙10^-6; n=10 эл. Р_ош.к.к.≈C²₁₀∙(2∙10^-6)²=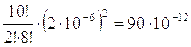

1.9 Пропускная способность канала связи

Для канала с постоянными параметрами, с единственной помехой в виде белого Гауссовского шума со спектральной плотностью мощности W₀, полоса частот которого равна ширине спектра сигнала: DF_к = DF_с, пропускная способность (максимально возможная скорость передачи информации по каналу при заданных характеристиках сигналов и помех) рассчитывается по формуле Шеннона для непрерывного Гауссовского канала без памяти:

С=DF_ар×log₂ (1+Р_с/Р_ш),        бит/с                                

где DF_к - полоса частот канала, равная ширине  спектра модулированного сигнала; DF_к=DF_мод. 

Р_с/ Р_ш - отношение сигнал/шум (мощностей сигнала и шума) на входе детектора.

Р_с=Р_тас=Е/Т_такт=Е×F_такт  және Е=h²×W₀                                                         

Р_ш=W₀×DF_ар=W₀×DF_ДЧМ және DF_ДЧМ =2×F_такт                                               

Тогда: Р_с/Р_ш=h²×W₀·F_такт/(W₀·2·F_такт)=h²/2                                                  

С=DF_ДЧМ×log₂ (1+h²/2)                                                                                

DF_ДЧМ=280 кГц=280∙10³ Гц; h²=50.

С=280×10³×log₂(1+50/2)=1,316×10⁶ бит/с=1,316 Мбит/с.

При увеличении полосы частот канала DF_к до бесконечности, пропускная способность канала стремится к пределу, называемому потенциально возможной пропускной способностью канала (теорема Шеннона):

С_¥=lim C =(Р_с/W₀)×log₂ е =1,443×(Р_с/W₀)                                

    DF_к→∞

Так как, Р_с=h²×W₀×F_такт   то:                                                                                             

С_¥=1,443×(h²×F_такт)                                                                             

h²=50; F_такт=70 кГц=70∙10³ Гц.

С_¥ =1,443×(50×70×10³)=5×10⁶ бит/с=5 Мбит/с.

Заключение

Потенциальная возможность пропускной способности канала по теореме Шеннона в 7,08 раз превышает пропускную способность реального канала нашей системы связи. Эффективность использования пропускной способности канала при оптимальном когерентном приеме высокопомехоустойчивых ДЧМ сигналов довольно высока, однако, еще имеется возможность ее увеличения путем использования более помехоустойчивых кодов и сокращения избыточности источника сообщений.

 

СПИСОК ЛИТЕРАТУРЫ

1. Теория электрической связи. Задание и методические указания на курсовую работу.- Алматы: АИЭС, 1998.- 11 с.

2. Панфилов И.П., Дырда В.Е. Теория электрической связи.– М.: Радио и связь, 1991

3. Емельянов Г.А., Шварцман В.О. Передача дискретной информации. - М.: Радио и связь, 1982

4. Передача дискретных сообщений / В.П. Шувалов и др. Под ред. В.П. Шувалова - М.: Радио и связь, 1990

5. Теория электрической связи. /А.Г. Зюко и др. Под ред. Д.Д. Кловского. - М.: Радио и связь, 1998

6. Пенин П.И., Филиппов Л.И. Радиотехнические системы передачи информации. - М.: Радио и связь, 1984.

7. ФС РК 10352-1910-У-е-001-2002 – Фирменный стандарт. Работы учебные. Общие требования к построению, изложению, оформлению и содержанию. – Алматы: АИЭС, 2002. – 34 с.