Краткое доказательство гипотезы Билля

Краткое доказательство гипотезы Билля

Гипотеза Билля формулируется следующим образом: неопределенное уравнение:

А^x +В^y= С^z                                                /1/

не имеет решения в целых положительных числах А, В, С, x, y и z при условии, что x, y и z больше 2.

Суть гипотезы Билля не изменится, если уравнение /1/ запишем следующим образом:

А^x = С^z - В^y                                                         /2/

Уравнение /2/ рассматриваем как параметрическое уравнение с параметром A и переменными B и С.

Уравнение /2/ запишем в следующем виде:

А^x = (С^0,5z)² – (В^0,5y)²                                 /3/

Обозначим:

В^0,5y =V                                                              /4/

С^0,5z =U                                                                         /5/

Отсюда:

В^y =V²                                                                         /6/

С^z =U²                                                                          /7/

В =                                                                         /8/

С =                                                                         /9/

Тогда из уравнений /2/, /6/ и /7/ следует:

А^x = С^z – В^y =U²-V²                                  /10/

Уравнение /10/ в соответствии с известной зависимостью для разности квадратов двух чисел запишем в виде:

А^x = (U-V)∙(U+V)                                      /11/

Для доказательства гипотезы Билля используем метод замены переменных. Обозначим:

U-V=X                                                      /12/

Из уравнения /12/ имеем:

U=V+X                                                     /13/

Из уравнений /11/, /12/ и /13/ имеем:

А^x = X· (V+X+V)=X (2V+X)=2VХ+X²             /14/

Из уравнения /14/ имеем:

А^x – X²=2VХ                                                               /15/

Отсюда:

V=                                    /16/

Из уравнений /13/ и /16/ имеем:

U= 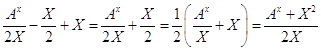 /17/

Из уравнений /8/, /9/, /16/ и /17/ имеем:

B =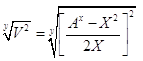                       /18/

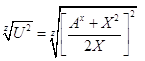C = /19/

Алгебраическое выражение  включает в себе возведение чисел в степень, вычитание одного числа из другого и деление их разности на число.

Алгебраическое выражение  включает в себе возведение чисел в степень, их сложение и деление суммы этих чисел на число.

Из анализа этих алгебраических выражений следует, что с помощью указанных математических действий нельзя получить числа, равные  и  соответственно, т.е.:

; /20/

, /21/

где: S и R – должны быть целыми числами.

Поэтому в соответствии с уравнениями /18/, /19/, /20/ и /21/:

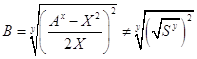 – дробное число;

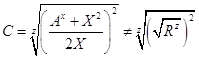 – дробное число.

Таким образом, числа В и С – дробные числа.

Следовательно, гипотеза Билля не имеет решения в целых положительных числах.