Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Самарский государственный аэрокосмический
университет имени академика С.П. Королёва
(национальный исследовательский университет)»

Кафедра теоретической механики

РЕФЕРАТ
Космические тросовые системы

Выполнил: студент группы 1405
Беляева Екатерина Александровна
Проверил: Асланов Владимир Степанович

Самара 2012

ОГЛАВНЕНИЕ

ВВЕДЕНИЕ. 3

Постановка задачи. 3

ПОДБОРКА ЛИТЕРАТУРЫ.. 5

ПРИМЕРЫ РЕШЕНИЯ ПОДОБНЫХ ЗАДАЧ. 6

Уравнения движения орбитальной тросовой системы с учетом колебаний космического аппарата. 6

Кинетическая энергия системы.. 7

Потенциальная энергия системы.. 8

Уравнения движения. 9

ПЛАН РАБОТЫ.. 10

ЗАКЛЮЧЕНИЕ. 11

ВВЕДЕНИЕ

Постановка задачи

Для доставки груза с орбиты на поверхность планет традиционно используются спускаемые аппараты и капсулы, переводимые на орбиту спуска с помощью реактивных двигателей. В последние десятилетия активно ведутся работы по созданию альтернативной схемы доставки груза с использованием космических тросовых систем, состоящих из космического аппарата (КА), троса и спускаемой (возвращаемой) капсулы с полезной нагрузкой (груз). Главным достоинством этой схемы является снижение стоимости осуществления маневра за счёт отказа от использования реактивного топлива.

Суть транспортной операции доставки груза с орбиты с помощью тросовой системы качественно можно описать следующим образом. С находящегося на орбите КА на гибком тросе в вертикальном направлении с некоторой скоростью выпускается груз. Под действием кориолисовой силы он отклоняется от местной вертикали в сторону направления движения КА. По мере увеличения длины троса высота груза над поверхностью Земли будет уменьшаться, а гравитационное ускорение, действующее на груз, будет увеличиваться по сравнению с аналогичным ускорением, действующим на КА. За счёт этого груз совершит возвратное движение. Находясь в окрестности местной вертикали КА, груз будет иметь скорость меньшую, чем скорость КА. Другими словами, за счёт возвратного движения груз получит отрицательное приращение к орбитальной скорости, эквивалентное тормозному импульсу. Если на этом этапе разорвать трос, то груз по определенной траектории совершит спуск в атмосферу.

В научной работе будет рассматриваться подобная космическая тросовая система, предназначенная для доставки грузов с орбиты. Будет построена математическая модель, исследована динамика ее движения, записаны уравнения движения космического аппарата и груза, а также уравнения движения груза в связанной системе координат. Будут представлены приближенно-аналитические решения и результаты численного моделирования.

ПОДБОРКА ЛИТЕРАТУРЫ

1.     Белецкий В.В., Иванов М.Б., Отставнов Е.И. Модельная задача о космическом лифте // Космические исследования - 2005 - №.2 - С.157-160. 

2.     Белецкий В.В., Левин Е.М. Динамика космических тросовых систем. М.: Наука, 1990 – 329 с.

3.     Белецкий В.В., Новикова Е.Т. Об относительном движении связки двух тел на орбите // Космич. исслед. 1969.  Вып. 3. С. 372–384.

4.     Алпатов А.П., Драновский В.И., Закржевский А.Е., Пироженко А.В., Хорошилов В.С. Космические тросовые системы. Обзор проблемы // Космічна наука і технологія. — 1997. — № 5/6. — С. 21–29

5.     Осипов В.Г., Шошунов Н.Л. Космические тросовые системы: история и перспективы // Земля и Вселенная – 1998. - №4. – С. 19-29

6.     Иванов В., Купреев С., Либерзон М. Космические тросовые системы. Некоторые аспекты практического пользования. М.: Сип Риа, 2005 – 100 с.

7.     Асланов В.С., Ледков А.С., Стратилатов Н.Р., Пространственное движение космической тросовой системы, предназначенной для доставки груза на Землю // Полет. – 2007. –  №2. – С.28-33.

ПРИМЕРЫ РЕШЕНИЯ ПОДОБНЫХ ЗАДАЧ

Уравнения движения орбитальной тросовой системы с учетом колебаний космического аппарата

В предлагаемой работе считается, что КА представляет собой твёрдое тело, совершающее движение центра масс и вокруг центра масс под действием гравитационной силы, гравитационного момента и момента от силы натяжения троса. Физическую модель будем определять следующим образом. КА задан как твёрдое тело с главными осями инерции; центр масс КА и точка выпуска в процессе развёртывания троса или точка крепления, когда трос уже выпущен, не совпадает с центром масс КА. Длина троса изменяется, масса троса пропорциональна длине. Концевой модуль – материальная точка. Математическая модель будет составлена с помощью корректного и весьма эффективного метода – уравнения Лагранжа второго рода. Следует учесть, что сила натяжения троса,  как правило, представляется управлением и является непотенциальной.

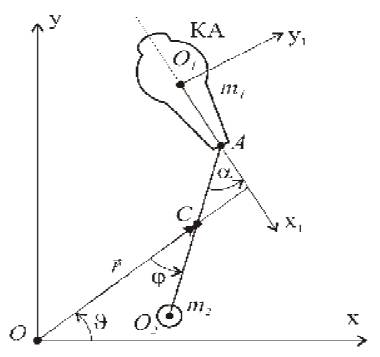
Рисунок 1 – Космический аппарат с тросовой системой

Рассматривается механическая система, включающая в себя космический аппарат (КА), весомый трос и концевой груз, представленные на рисунке 1. КА представляется как твёрдое тело, совершающее движение центра масс и вокруг центра масс под действием гравитационного момента и момента от силы натяжения троса. С помощью уравнения Лагранжа второго рода получена математическая модель плоского движения представленной механической системы.

Кинетическая энергия системы

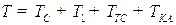,                                                                  (1.1)

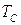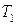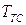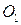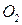где  - кинетическая энергия центра масс системы,  - кинетическая энергия, связанная с удлинением троса,  - кинетическая энергия вращения весомого троса и двух материальных точек  и  массой, соответственно,  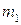и 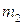относительно центра масс системы С,  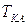- кинетическая энергия относительного вращения аппарата.

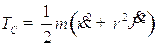,                                                                       (1.2)

где 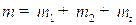 - полная масса системы: 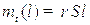- масса троса (  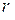- плотность троса, S - площадь поперечного сечения троса),  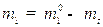- текущая масса КА,  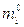- начальная масса КА.

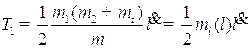         ,                                                     (1.3)

где 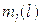- редуцированная масса троса.

         ,                                                                               
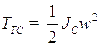   (1.4)

где 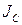 - момент инерции тросовой системы, а  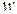- абсолютная угловая скорость, которая для выбранных обобщенных координат (Рисунок 1) выражается .

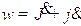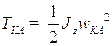         ,                                                                                (1.5)

где 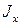,,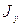 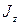- главные моменты инерции КА в связанной системе координат, а .

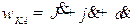         Подставляя (1.2 – 1.5) в (1.1), получим:

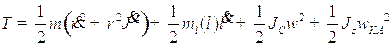.                        (1.6)

Потенциальная энергия системы

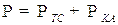         ,                                                                               (1.7)

где 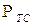 - потенциальная энергия тросовой системы,  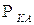- потенциальная энергия для твёрдого тела (КА) в центральном поле.

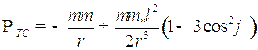,                                                   (1.8)

где 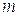 - гравитационный параметр, а  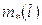- редуцированная масса тросовой системы.

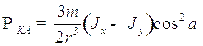         .                                                              (1.9)

         Подставляя (1.8 – 1.9) в (1.7), получаем:

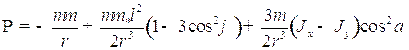         .                     (1.10)

Уравнения движения

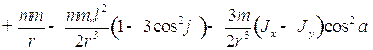.                                     (1.11)

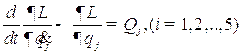         ,                                                      (1.12)

где 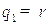, , 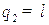, , 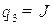, 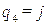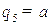а 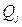 - обобщенные силы.

         Уравнениям Лагранжа второго рода отвечают четыре дифференциальных уравнения движения второго порядка:

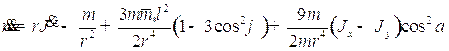         ,             (1.13)

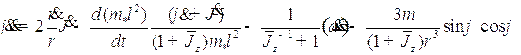         , (1.14)

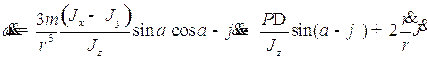         ,                   (1.15)

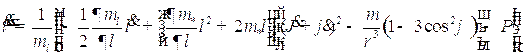         ,(1.16)

и один первый интеграл:

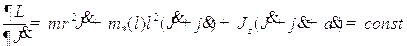         .                     (1.17)

ПЛАН РАБОТЫ

1.     Исследовать проблемы и перспективы такой области космической техники как космическая тросовая система.

2.     Рассмотреть подобные задачи с их решениями.

3.     Построить плоскую модель космической тросовой системы: записать уравнения движения космического аппарата, уравнения движения груза, уравнения движения груза в связанной системе координат.

4.     Исследовать движение космического аппарата относительно центра масс под действием силы натяжения троса. Найти приближенно-аналитические решения, привести результаты численного моделирования.

5.     Рассмотреть нештатные ситуации, исследовать возможность их появления, рассмотреть случай заклинивания троса.

ЗАКЛЮЧЕНИЕ

Результатами работы будут полученные уравнения движения космической тросовой системы, будут построены графики этого движения при различных начальных условиях, приведены таблицы найденных значений, и на их основе будут сформулированы полезные выводы для продолжения работы над проблемой космических тросовых систем.

Полученные в результате этой научной работы математические модели и приближенные аналитические решения позволят провести исследование движения системы, состоящей из спутника, троса и спускаемого аппарата, с момента отделения спускаемого аппарата до его посадки. Они могут быть полезны при разработке новых транспортных систем для доставки груза на Землю.