Кинематические и динамические характеристики. Определение.

Содержание;

Вращательное движение;

Определение.

   Кинематические характеристики

   Динамические характеристики

Момент инерции;

   Определение.

   Осевой момент инерции.

   Теорема Гюйгенса-Штейнера.

   Центробежный момент инерции

   Геометрический момент инерции.

   Тензор и эллипсоид инерции

Используемая литература

 

 

Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.

При выборе некоторых осей вращения, можно получить сложное вращательное движение — сферическое движение, когда точки тела движутся посферам.

Кинематические характеристики

Вращение твердого тела, как целого характеризуется углом 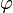, измеряющегося в угловых градусах или радианах, угловой скоростью  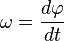(измеряется в рад/с) иугловым ускорением  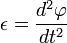(единица измерения - рад/с²).

При равномерном вращении (T оборотов в секунду),

 Частота вращения — число оборотов тела в единицу времени.

,

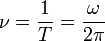Период вращения — время одного полного оборота. Период вращения T и его частота 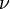 связаны соотношением .

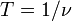Линейная скорость точки, находящейся на расстоянии R от оси вращения

,

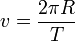Угловая скорость вращения тела

 .

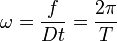Динамические характеристики

Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные изуравнений Гамильтона или Лагранжа. Кинетическую энергии вращения можно записать в виде 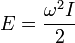. В этой формуле момент инерции играет роль массы, а угловая скорость роль обычной скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы .

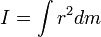Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

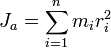где: m_i — масса i-й точки, r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.

Кинетическая энергия вращательного движения

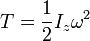
где I_z — момент инерции тела относительно оси вращения. 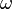 — угловая скорость

Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.

Осевой момент инерции

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

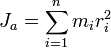где:

·                    m_i — масса i-й точки,

·                    r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, какмасса тела является мерой его инертности в поступательном движении.

,

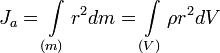где:

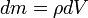·                     — масса малого элемента объёма тела ,

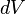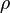·                     — плотность,

·                     — расстояние от элемента 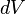 до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

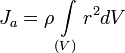
Теорема Гюйгенса-Штейнера

Основная статья: Теорема Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_cотносительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

,

где 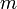 — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

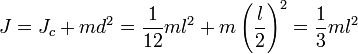
Центробежный момент инерции

Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:

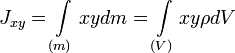
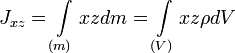
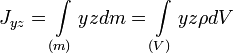
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.

Ось OX называется главной осью инерции тела, если центробежные моменты инерции J_xy и J_xz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.

Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — егоглавными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.

Центральный момент инерции

Центральный момент инерции 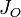 (или момент инерции относительно точки O) — это величина

,

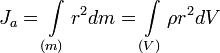где:

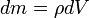·                     — масса малого элемента объёма тела ,

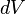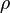·                     — плотность,

·                     — расстояние от элемента 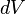 до точки O.

Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .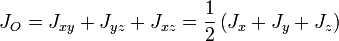

Геометрический момент инерции

Геометрический момент инерции — геометрическая характеристика сечения вида

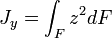
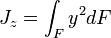
где 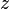 — расстояние от центральной оси  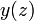до любой элементарной площадки  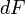относительно нейтральной оси.

Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции,прогиба балки, подбора сечения балок, колонн и др.

Единица измерения СИ — м⁴. В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см⁴.

Из него выражается момент сопротивления сечения:

.

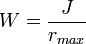Тензор и эллипсоид инерции

Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором 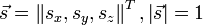, можно представить в виде квадратичной (билинейной) формы:

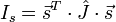 (1),

где 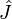 — тензор инерции. Матрица тензора инерции симметрична, имеет размеры  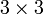и состоит из компонент центробежных моментов:

 , 
.

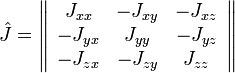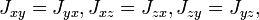
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :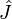
 ,
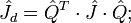
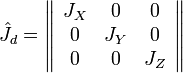где 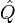 — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины  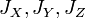— главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:

,

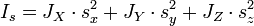откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на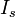 

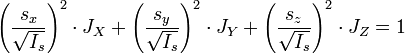
и произведя замены:

,

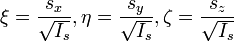получаем канонический вид уравнения эллипсоида в координатах :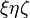

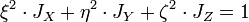
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:

Используемая литература

Б. Яворский А. Детлаф, Физика, М.: Дрофа, 1998.

Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)

Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.

Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997.

Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.

Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. 

Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. 

Беляев Н. М., Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.