Министерство образования и науки Российской Федерации
ФГАОУ ВПО «Северо-Восточный федеральный университет им. М.К. Аммосова»
Технологический институт
Кафедра «Многоканальные телекоммуникационные системы»
Курсовая работа
По дисциплине: Электромагнитные поля и волны
Тема: Исследование распространения электромагнитных волн в реальных средах
Выполнил:
студент 2 курса группы
ИТСС-14(А) ТИ СВФУ
(специальность: «Инфокоммуникационные технологии и системы связи»)
Чулуунхуу A.
Проверил:
Доцент,Кандидат физико-математических наук
Бороев Р. Н.
Якутск
2016г.
Оглавление
Задание: 3
Исходные данные. 3
Введение. 4
Теоретические сведения. 5
Волновой процесс. 5
Плоская электромагнитная волна. 5
Заключение. 19
Список литературы.. 19
Задание: Исследование влияния параметров реальных сред на процесс распространения электромагнитных волн в волноводе.
Для
прямоугольного волновода сечением ab мм, заполненного различными средами (см.
таблицу 2), рассчитать для заданных в таблице 1 вариантов частоты f :
коэффициент затухания α, фазовую постоянную β, модуль характеристического
сопротивления , длину волны λ и фазовую скорость в прямоугольном
волноводе, заполненного средой. Определить эквивалентную проводимость среды 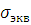 .
В качестве исследуемых сред используются немагнитные среды. Относительная
магнитная проницаемость μ для немагнитных сред всегда равна единице μ
=1,
.
В качестве исследуемых сред используются немагнитные среды. Относительная
магнитная проницаемость μ для немагнитных сред всегда равна единице μ
=1, 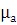 =
=
 .
.
Исходные данные
Вариант 25
|
Частота ГГц |
8,55 |
|
Среда |
|
|
μ |
|
Текстолит |
3,0 |
7,8.10-2 |
1 |
|
Дерево |
1,7 |
2,65.10-2 |
1 |
|
Оргстекло |
2,5 |
1,2.10-2 |
1 |
Введение
Электромагнитные волны — электромагнитные колебания, распространяющиеся в пространстве с конечной скоростью, зависящей от свойств среды. Электромагнитной волной называют распространяющееся электромагнитное поле.
Существование электромагнитных волн было предсказано М.
Фарадеем еще в 1832 году. Дж. Максвелл 1865 году в результате анализа предложенной им
системы, описывающей электромагнитное поле, теоретически показал, что
электромагнитное поле в вакууме может существовать и в отсутствие источников —
зарядов и токов. Поле без источников имеет вид волн, распространяющихся с
конечной скоростью, которая в вакууме равна скорости света: с = 299792458±1,2 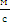 . Совпадение
скорости распространения электромагнитных волн в вакууме с измеренной ранее
скоростью света позволило Максвеллу сделать вывод о том, что свет представляет
собой электромагнитные волны. Подобное заключение в дальнейшем легло в основу
электромагнитной теории света.
. Совпадение
скорости распространения электромагнитных волн в вакууме с измеренной ранее
скоростью света позволило Максвеллу сделать вывод о том, что свет представляет
собой электромагнитные волны. Подобное заключение в дальнейшем легло в основу
электромагнитной теории света.
В 1888 году теория электромагнитных волн получила экспериментальное подтверждение в опытах Г. Герца. Используя источник высокого напряжения и вибраторы, Герцу удалось выполнить тонкие эксперименты по определению скорости распространения электромагнитной волны и ее длины. Экспериментально подтвердилось, что скорость распространения электромагнитной волны равна скорости света, что доказывало электромагнитную природу света.
В электродинамике электромагнитное поле описывается четырьмя http://www.physics.ru/courses/op25part2/content/chapter2/section/paragraph6/theory.html#.VxnPGtR97IU
уравнениями Максвелла, благодаря которым существует возможность единым
образом подойти к описанию радиоволн, света, рентгеновских лучей и гамма-излучения. Оказалось, что они представляют собой не излучения различной природы, а электромагнитные волны с различной длиной волны.
Электромагнитное поле — это вид материи, связанный с изменением и непрерывным взаимным превращением магнитного и электрического полей и характеризующийся способностью распространяться в вакууме со скоростью, близкой к
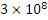 м/сек,
способностью силового воздействия на заряженные частицы, токи и на определенным
образом ориентированную поверхность вещества. Электромагнитное поле в одних
случаях характеризуется непрерывным распределением в пространстве, а в других
случаях обнаруживает дискретность своей структуры.
м/сек,
способностью силового воздействия на заряженные частицы, токи и на определенным
образом ориентированную поверхность вещества. Электромагнитное поле в одних
случаях характеризуется непрерывным распределением в пространстве, а в других
случаях обнаруживает дискретность своей структуры.
Теория электромагнитного поля представляет собой учение об электрических и магнитных явлениях, о теоретических положениях и законах, которым подчиняются эти явления, и о вытекающих из них методах расчета.
http://www.b-i-o-n.ru/theory/elektromagnitnye-volny/
Теоретические сведения
Волновой процесс – это возмущение некоторой величины в пространстве, перемещающееся с конечной скоростью и переносящее энергию без переноса вещества.
Математически волновой процесс описывается однородным уравнением Гельмгольца:
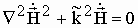 ,
(1)
,
(1)
где 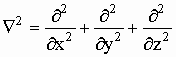 -
оператор Лапласа,
-
оператор Лапласа,
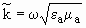 - волновое
число или постоянная распространения,
- волновое
число или постоянная распространения,
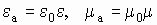 -
абсолютные диэлектрическая и магнитная проницаемости,
-
абсолютные диэлектрическая и магнитная проницаемости,
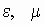 - относительные
диэлектрическая и магнитная проницаемости.
- относительные
диэлектрическая и магнитная проницаемости.
Плоская
электромагнитная волна – это волновой процесс, у которого электрическая и
магнитная составляющие поля во всех точках плоскости, перпендикулярной
направлению распространения волны, имеют одинаковые значения. Если принять в
качестве направления распространения плоской электромагнитной волны ось z в
декартовой системе координат, то, согласно определению, поле плоской
электромагнитной волны не зависит от поперечных координат x и y.,
следовательно, 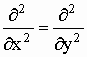 и
уравнение (1) принимает следующий вид:
и
уравнение (1) принимает следующий вид:
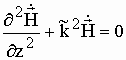 .
.
Решение данного дифференциального уравнения 2-го порядка имеет вид:
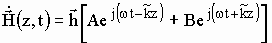 , (2)
, (2)
где 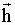 –
единичный вектор.
–
единичный вектор.
Общее решение представляет собой два волновых процесса, распространяющихся на встречу друг друга, вдоль отрицательного и положительного направления оси z (волна падающая и отраженная). Поскольку в рассматриваемой задаче рассматривается один источник, то учитываем только волну с амплитудой А
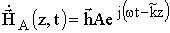 . (3)
. (3)
Выделим из комплексного выражения действительную часть:
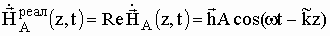 .
.
Идеальная среда
Идеальной средой принято называть среду в которой отсутствуют потери энергии при распространении электромагнитной волны. Общая запись плоской электромагнитной волны в идеальной среде:
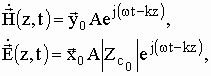 (4)
(4)
где k – вещественное волновое число.
Вектор напряженности
магнитного поля перпендикулярен вектору напряженности электрического поля.
Электрическое и магнитное поля колеблются в пространстве синхронно и синфазно.
Коэффициент пропорциональности, определяемый как 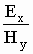 ,
называется характеристическим (волновым) сопротивлением данной среды
,
называется характеристическим (волновым) сопротивлением данной среды 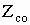 :
:
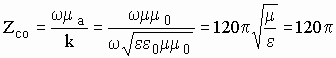 . (5)
. (5)
Из (5) видно, что 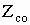 полностью
определяется лишь параметрами самой среды.
полностью
определяется лишь параметрами самой среды.
Перейдем от комплексных значений в (4) к мгновенным, в результате получим:
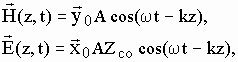 (6)
(6)
где 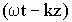 -
фаза колебаний.
-
фаза колебаний.
Длина волны 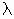 - это
расстояние, которое проходит фазовый фронт за один период колебаний высокой
частоты. Отсюда фазовая скорость плоской электромагнитной волны в идеальной
среде равна:
- это
расстояние, которое проходит фазовый фронт за один период колебаний высокой
частоты. Отсюда фазовая скорость плоской электромагнитной волны в идеальной
среде равна:
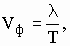
 ,
,
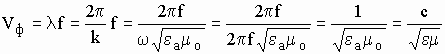 , (7)
, (7)
где: 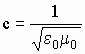 -
скорость света.
-
скорость света.
Плоская электромагнитная волна в реальной среде.
При распространении электромагнитных волн в реальных средах происходит частичное рассеивание их энергии, которое обусловлено потерями в среде. Различают два вида потерь в среде:
Поляризационные (диэлектрические) потери. Механизм их
появления можно пояснить следующим образом. При отсутствии внешнего
электрического поля каждый атом вещества, из которого состоит среда, упрощенно
представляет собой положительно заряженное ядро с отрицательными электронами,
вращающимися по круговой орбите. Центры положительного и отрицательного зарядов
совпадают и суммарный заряд атома равен нулю. Под влиянием внешнего
электрического поля орбита электрона (электронов) вытягивается, стремясь к
эллиптической. В этом случае центры положительного и заряда перестают совпадать
друг с другом и атом начинает вести себя подобно электрическому диполю. Диполи
отдельных атомов всего вещества ориентируются определенным образом относительно
приложенного внешнего поля. Этот процесс принято называть электронной
поляризацией. В переменном электрическом поле ориентация диполей меняется с
частотой 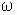 ,
возникающие при этом “трения” при смещении отдельных диполей вещества и
обуславливают поляризационные (диэлектрические) потери. Их учет производится
путем введения комплексной абсолютной диэлектрической проницаемости:
,
возникающие при этом “трения” при смещении отдельных диполей вещества и
обуславливают поляризационные (диэлектрические) потери. Их учет производится
путем введения комплексной абсолютной диэлектрической проницаемости:
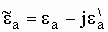 ,
,
где 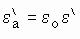 .
.
Потери, обусловленные проводимостью вещества. Они
возникают вследствие столкновения свободных носителей заряда (электронов) с
атомами кристаллической решетки. Поскольку упорядоченное движение электронов
создает электрический ток, называемый током проводимости, то принято говорить,
что данный вид потерь обусловлен протеканием в среде токов проводимости. Эти
потери в среде пропорциональны отношению удельной электрической проводимости 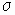 к
частоте поля
к
частоте поля 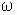
.
При фиксированной частоте эти два вида потерь с макроскопической точки зрения неразличимы: как те так и другие потери приводят к преобразованию электромагнитной энергии в другие виды энергий. Вследствие этого комплексная диэлектрическая проницаемость среды с учетом обеих видов потерь запишется как:
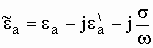 .
.
Можно формально ввести понятие эквивалентной проводимости
среды, соответствующую поляризационным потерям как:  .
.
Отсюда: 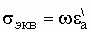 .
.
Тогда окончательно получаем:
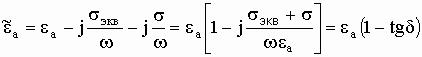 . (8)
. (8)
Отношение 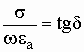 -
носит название тангенса угла потерь.
-
носит название тангенса угла потерь.
Отношение 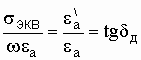 -
носит название тангенса угла диэлектрических потерь.
-
носит название тангенса угла диэлектрических потерь.
Разделение сред на диэлектрические и проводящие с физической точки зрения связанно с наличием свободных носителей заряда. В то же время можно сказать, что разделение сред на диэлектрики и проводники достаточно условно, поскольку одна и та же среда может вести себя по-разному на различных частотах (например, морская вода на НЧ является проводником, а на СВЧ – диэлектриком).
В данной лабораторной работе исследуются диэлектрические
среды, для которых справедливо неравенство 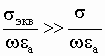 ,
поэтому:
,
поэтому:
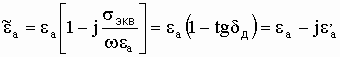 . (9)
. (9)
Вследствие этого, волновое число также является комплексной величиной:
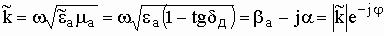 .
(10)
.
(10)
Вещественную часть волнового числа β называют фазовой постоянной, а мнимую часть α - коэффициентом затухания. Значения β и α можно найти непосредственно из (10):
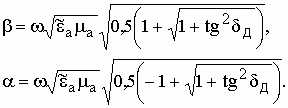 (11)
(11)
Таким образом, с учетом выражений (4) и (10) уравнение плоской электромагнитной волны в реальной безграничной среде запишется как:
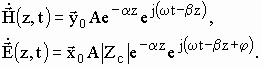
Перейдем к мгновенным значениям 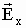 и
и 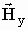 , в
результате получим:
, в
результате получим:
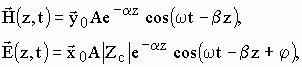 (12)
(12)
где 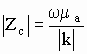 -
модуль характеристического сопротивления реальной среды,
-
модуль характеристического сопротивления реальной среды,
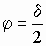 -
сдвиг по фазе.
-
сдвиг по фазе.
Сравнивая уравнения (6) и (12), можно выявить следующие различая между плоской электромагнитной волной в идеальной и реальной среде:
а) Векторы Е и Н сдвинуты по фазе на угол, равный j ;
б) Множитель 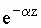 указывает
на экспоненциальное ослабление поля в направлении распространения волны, что
связанно с преобразованием части электромагнитной энергии в другие виды
энергий. Отсюда очевиден физический смысл коэффициента затухания: a
характеризует уменьшение амплитуды волны на единицу длины.
указывает
на экспоненциальное ослабление поля в направлении распространения волны, что
связанно с преобразованием части электромагнитной энергии в другие виды
энергий. Отсюда очевиден физический смысл коэффициента затухания: a
характеризует уменьшение амплитуды волны на единицу длины.
в) Роль волнового числа (постоянной распространения) электромагнитной волны в постоянной среде играет вещественная часть b комплексного волнового числа. Постоянная распространения b характеризует изменение фазы волны на единицу длины. По аналогии с идеальной средой, для реальной среды длина волны и фазовая скорость будут определяться как:
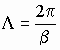 ,
, 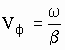 .
(13)
.
(13)
В заключении изобразим мгновенную картину плоской электромагнитной волны, распространяющейся в идеальной среде (рис. 2 а) и в реальной среде (рис. 2б).
Графики волны в идеальной и реальной среде.
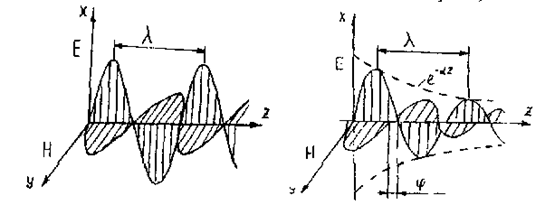
а)
б)
Рисунок 2 – Эскиз взаимного расположения электрических и магнитных полей в пространстве, а) в идеальных средах б) в реальных средах
Плоская электромагнитная волна в направляющей системе.
Для исследования поведения плоских электромагнитных волн в реальной среде в данной лабораторной работе используется направляющая система, позволяющая сосредоточить электромагнитную энергию в определенном пространстве и передать ее в заданном направлении. Примером направляющей системы может, в частности, служить полая металлическая труба прямоугольного сечения, носящая название прямоугольный волновод. Электромагнитное поле в прямоугольном волноводе можно рассматривать как результат сложения плоских электромагнитных волн, рассмотренных ранее, многократно отраженных под углом g от граничных поверхностей, образующих волновод (см. рис. 3).
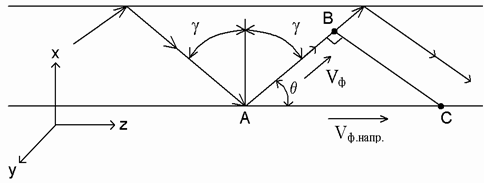
Рисунок 3 – Электромагнитное поле в прямоугольном волноводе
Плоская электромагнитная волна, двигаясь от точки А до точки
В, за время 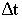 пройдет
расстояние АВ равное
пройдет
расстояние АВ равное 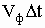 . За
это же время волна вдоль стенки волновода пройдет расстояние
. За
это же время волна вдоль стенки волновода пройдет расстояние 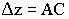 и
равное
и
равное 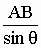 .
Таким образом:
.
Таким образом: 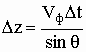 ,
фазовая скорость электромагнитной волны в направляющей системе:
,
фазовая скорость электромагнитной волны в направляющей системе:
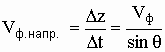 .
.
Так как 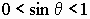 , то
отличительной особенностью направляющих систем является то, что фазовая
скорость распространения электромагнитной волны в них больше чем фазовая
скорость волны в неограниченной среде. В частности, для прямоугольного
волновода:
, то
отличительной особенностью направляющих систем является то, что фазовая
скорость распространения электромагнитной волны в них больше чем фазовая
скорость волны в неограниченной среде. В частности, для прямоугольного
волновода:
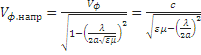 , (14)
, (14)
где: 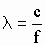 -
длина волны в свободном пространстве;
-
длина волны в свободном пространстве;
а – размер широкой стенки прямоугольного волновода.
Исходя из (13) и (14) нетрудно определить основные параметры электромагнитной волны в прямоугольном волноводе, заполнено реальной средой:
Постоянная распространения волны в прямоугольном волноводе b :
, 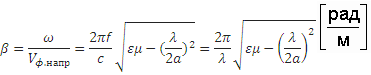
. (15)
Длина волны в прямоугольном волноводе 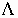 :
:
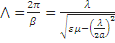 ,
, 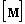 .
(16)
.
(16)
Модуль характеристического сопротивления прямоугольного волновода:
 . (17)
. (17)
Коэффициент затухания a в прямоугольном волноводе:
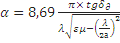 ,
, 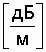 .
(18)
.
(18)
На практике, чтобы определить затухание волны 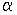 в
прямоугольном волноводе при прохождении пути L, берут отношение амплитуд на
концах этого участка:
в
прямоугольном волноводе при прохождении пути L, берут отношение амплитуд на
концах этого участка:
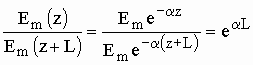 .
.
Затухание в децибелах определяют, как двадцать десятичных логарифмов от этого отношения:
 .
.
Отсюда:
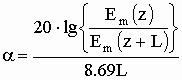 ,
, 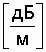 .
(19)
.
(19)
Расчетная часть
Расчет коэффициента затухания в прямоугольном волноводе
Для расчета коэффициента затухания, воспользуемся формулой:

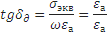
Для текстолита:
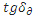 =
=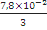 =0,026
=0,026
Для дерева:
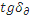 =
=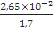 =0,0155
=0,0155
Для Оргстекла:
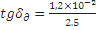 =0.0048
=0.0048
длину волны в свободном пространстве на заданной частоте для расчета коэффициента затухания определил так:
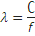
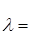
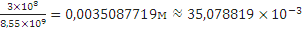
Для текстолита:
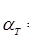
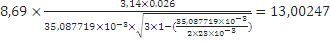
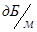
Для дерева:
 =
=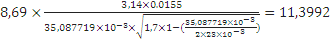
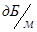
Для оргстекла:
 =
=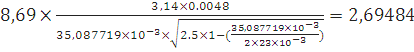
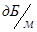
Расчет фазовой постоянной в прямоугольном волноводе
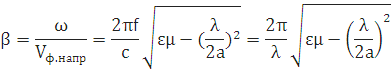
Для текстолита:

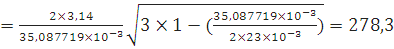

Для дерева:

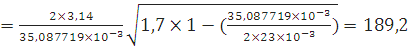

Для оргстекла:

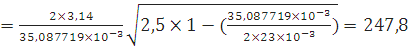

Расчет длины волны в прямоугольном волноводе
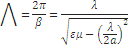
Для текстолита:

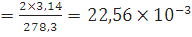
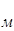
Для дерева:

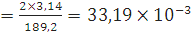
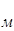
Для оргстекла:

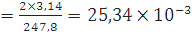
Расчет фазовой скорости в прямоугольном волноводе
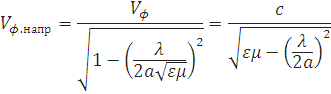
Фазовая
скорость 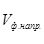 в прямоугольном волноводе
определяется
в прямоугольном волноводе
определяется
, 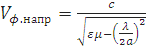
Для текстолита:
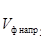


Для дерева:
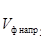
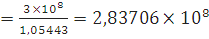

Для оргстекла:
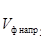
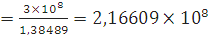

Расчет модуля характеристического сопротивления в среде с относительной диэлектрической проницаемостью e
Для тексолита:
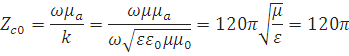
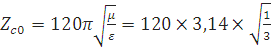 =217,55
=217,55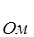
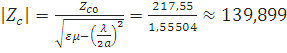
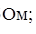
Для дерева:
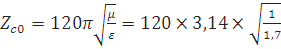 =288,99
=288,99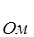
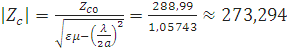
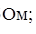
Для оргстекла:
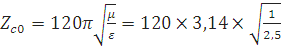 =238,28
=238,28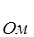
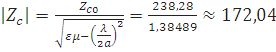
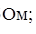
Расчет эквивалентной проводимости среды
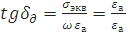 т.е
т.е
 /
/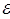
тогда 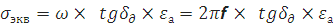
Для текстөлита:
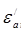

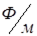
Для дерева:
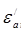
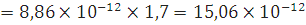
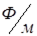
Для оргстекла:
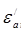
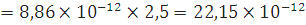
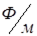
Эквивалентная проводимость среды тогда будет равна
Для текстолита:
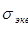
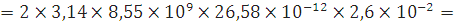
 См/м
См/м
Для дерева:
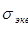

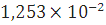 См/м
См/м
Для оргстекла:
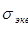

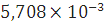 См/м
См/м
Заключение
Выявили,
что параметры волны (α, β, Λ,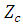 ,)
распространяющейся в среде с потерями, практически мало отличаются от
параметров волны в идеальной среде (среде без потерь), с теми же значениями
,)
распространяющейся в среде с потерями, практически мало отличаются от
параметров волны в идеальной среде (среде без потерь), с теми же значениями  и
и
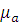 ,
но зависят от частоты, а в идеальной среде не зависят.
,
но зависят от частоты, а в идеальной среде не зависят. 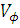 также
зависит от частоты.
также
зависит от частоты.
Список литературы
1. Учебно-методическое пособие <<Физика волновы процессов>> ав. Г.Е Корчагин , А.А. Журавлев, Ю.М. Стенин , Казань 2014г.
2. Гольдштейн А.Д., Зернов Н.В. Электромагнитные поля и волны. – М.: Советское радио, 1971.
3. Брунов В.Н., Гольдберг Л.Н., Кляцкин Н.Г., Цейтлин Л.А. Теория электромагнитного поля. – М.: Госэнергоиздат, 1962.
4. Семенов Н.А. Техническая электродинамика. – М.: Связь, 1973.
5. Лекции по курсу «Электромагнитные поля и волны».














 (zip - application/zip)
(zip - application/zip)










