Министерство образования и науки РФ
Государственное образовательное учреждение
Высшего профессионального образования
Московской области
Международный Университет природы
общества и человека "Дубна"
Филиал "Котельники"
Кафедра естественных и гуманитарных наук.
Курсова робота
"Исследование прочности на разрыв полосок ситца"
по дисциплине:
"Теория вероятностей и математическая статистика"
Выполнила студентка
Второго курса 262 ЭТ группы
Проверила:
___________
2006 г.
Содержание
Распределение случайной величины на основе опытных данных
Построение эмпирической функции распределения
Статистические оценки параметров распределения
Нормальный закон распределения случайной величины
Проверка гипотезы о нормальном распределении изучаемой величины
Введение
Математическая статистика - наука которая занимается разработкой методов отбора, группировки и обработки опытных данных с целью изучения закономерностей массовых случайных явлений.
Математическая статистика опирается на методы и понятия теории вероятностей и, в свою очередь, служит основой для обработки анализа статистических результатов в конкретных областях человеческой деятельности.
Задачи математической статистики:
нахождение функции распределения по опытным данным.
из теоретических соображений функция распределения оказывается в общем виде известна, но неизвестны её параметры. Неизвестные параметры определяются по опытным данным.
Статистическая проверка гипотез:
в общем виде известна функция распределения, определяют её неизвестные параметры и выясняют, как согласуются экспериментальные данные с общим видом функции распределения.
Цель курсовой работы
Целью курсовой работы является закрепление теоретических знаний и приобретения навыков обработки статистической информации.
Постановка задачи
В данной курсовой работе были поставлены следующие задачи для обработки статистических данных:
построение полигона частот и относительных частот
построение гистограммы частот и относительных частот
построение эмпирической функции распределения.
нахождение выборочной средней, выборочной дисперсии и
нахождение среднего выборочного квадратичного отклонения.
5) проверка гипотезы о нормальном распределении изучаемой случайной величины.
Исходные данные
Вариант 14. Прочность на разрыв полосок ситца (в дан):
32313432312932343331313432313532
34333130303232343131353234333231
34323129323433313134323135323433
31303432312932343331303232313632
34333130323331283234333130323330
35323433323031333033323433313032
33303132343331303233303132333331
30323330313233303433313032333031
3233
Распределение случайной величины на основе опытных данных
Для обработки опытных данных воспользуемся составлением статистического ряда. В первой строке записываются номера наблюдений, а во второй строке результаты наблюдений.
Если результаты наблюдений расположить в возрастающем порядке, то получим вариационный ряд.
Результат измерения называется - варианта.
Число появления каждой варианты называется частотой.
Отношение частоты к объему выборки называется относительной частотой.
xi - варианта (значение, полученное в процессе измерения)
ni - частота (сколько раз появилась каждая варианта)
Р*i - отношение частоты объёму выборки
|
xi |
28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
|
ni |
1 | 3 | 18 | 29 | 32 | 24 | 18 | 4 | 1 |
|
ni
|
1
|
3
|
18
|
29
|
32
|
24
|
18
|
4
|
1
|
Существует вместо статистического ряда так называемая статистическая совокупность, для этого все наблюдаемые значения признака разбиваются на группы равной длины.
|
xi<x≤xi+1 |
(27; 29] | (29; 31] | (31; 33] | (33; 35] | (35; 37] |
|
ni |
4 | 47 | 56 | 22 | 1 |
|
Pi* |
4/130 | 47/130 | 56/130 | 22/130 | 1/130 |
Размах колебания: хmin=28
хmax=36
R= 36-28=8
Статистическое распределение можно изобразить графически:
Либо в виде полигона частот, полигона относительных частот и в виде гистограммы частот, гистограммы относительных частот.
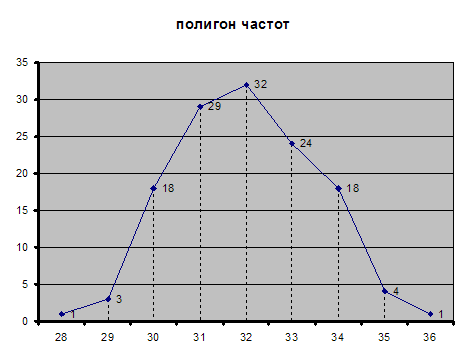
Полигоном частот называется ломаная линия, соединяющая точки с абcциcсой (Ох) - варианта и ординатой (Оу) - частота.
Cтроим полигон частот.
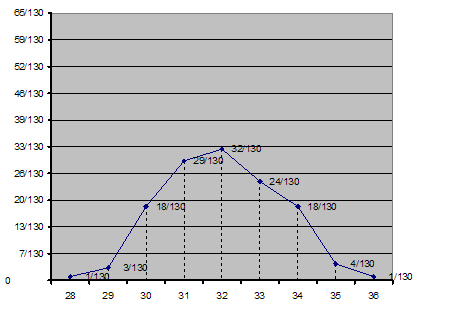
Полигоном относительных частот называется ломаная линия, соединяющая точки с абсциссой (Ох) - варианта и ординатой (Оу) - относительная частота.
Строим полигон относительных частот.
Полигон относительных частот
Гистограммой частот называется фигура, состоящая из прямоугольников с равными основаниями (длина интервала) и площадью численно равной частоте.
Для построения гистограммы воспользуемся таблицей:
|
xi |
(27; 29] | (29; 31] | (31; 33] | (33; 35] | (35; 37] |
|
ni |
4 | 47 | 56 | 22 | 1 |
|
Δx |
4/2 | 47/2 | 56/2 | 22/2 | ½ |
|
|
Δx=2 | ||||||||
| hi | |||||||||
| 56⁄ 2 | |||||||||
| 47⁄ 2 | |||||||||
| 22⁄ 2 | |||||||||
| 4/2 | |||||||||
| 1/2 | |||||||||
| 27 | 29 | 31 | 33 | 35 | 37 | ||||
| xi |
Гистограммой относительных частот называется фигура, состоящая из прямоугольников с равными основаниями (длина интервала) и площадью численно равной относительной частоте.
Для построения гистограммы воспользуемся таблицей:
|
xi |
(27; 29] | (29; 31] | (31; 33] | (33; 35] | (35; 37] |
|
Р*i |
4/130 | 47/130 | 56/130 | 22/130 | 1/130 |
|
Δx |
4/260 | 47/260 | 56/260 | 22/260 | 1/260 |
Δx=2
|
|
|||||||||
| h*i | |||||||||
| 56∕ 260 | |||||||||
| 47⁄ 260 | |||||||||
| 22⁄ 260 | |||||||||
| 4∕ 260 | |||||||||
| 1 ∕ 260 | |||||||||
| 0 | 27 | 29 | 31 | 33 | 35 | 37 | |||
| xi | |||||||||
Построение эмпирической функции распределения
Статистическая функция распределения (эмпирическая) - это частота события, состоящего в том, что случайная величина Х в процессе изменения примет значение меньше некоторого фиксированного х
F*(х) = Р* = P* (X Статистическая функция распределения (эмпирическая) является
разрывной функцией, точки разрыва совпадают с наблюдаемыми значениями случайной
величины, а скачок в каждой точке разрыва равен частоте появления наблюдаемого
значения в данной серии наблюдения. Сумма скачков всегда равна 1. 9 Σ
Pi* = 1 i=1 1) ∞ < х ≤
28 F* (x) =P* (X<28) =0 2) 28 F* (x) =P* (X<29) =P*
(X=28) =1/130 3) 29 F* (x) =P* (X=28) + P*
(X=29) =1/130+3/130=4/130 4) 30 F* (x) =P* (X<31) =
P* (X=28) + P* (X=29) P* (X=30) +1/130+3/130+18/130=22/130 5) 31 F* (x) =P* (X<32) =
P* (X=28) + +P* (X=29) +P* (X=30) +P*
(X=31) =1/130+3/130+18/130+29/130=51/130 6) 32 F* (x) =P* (X<33) =
P* (X=28) +P* (X=29) +P* (X=30) +P*
(X=31) P* (X=32) =1/130+3/130+18/130+29/130+32/130=83/130 7) 33 F* (x) =P* (X<34) =
P* (X=28) +P* (X=29) +P* (X=30) +P*
(X=31) + +P* (X=32) +P* (X=33) =1/130+3/130+18/130+29/130+32/130+24/130=107/130 8) 34 F* (x) =P* (X<35) =
P* (X=28) +P* (X=29) +P* (X=30) +P*
(X=31) + +P* (X=32) +P* (X=33)
P* (X=34) = =1/130+3/130+18/130+29/130+32/130+24/130+18/130=125/130 9) 35 F* (x) =P* (X<36) =
P* (X=28) +P* (X=29) +P* (X=30) +P*
(X=31) + +P* (X=32) +P* (X=33)
P* (X=34) + P* (X=35) =1/130+3/130+18/130+29/130+32/130+24/130+18/130+4/130=129/130 10) x>36 F* (x) =1 1/130, -∞<х≤29 4/130, 29<х≤30 22/130, 30<х≤31 F*(x) 51/130, 31<х≤32 83/130, 32<х≤33 107/130, 33<х≤34 125/130, 34<х≤35 129/130, 35<х≤36 1, х>36 Статистическая функция распределения является разрывной
функцией и её графиком является ступенчатая линия. Построим систему координат: на оси Ох=хi на оси Оу=F* (x)
F* Одной из задач статистики является оценка параметров
распределения случайной величины Х по данным выборки. Оценка параметра зависит от наблюдаемых значений и от числа
наблюдений. Для того чтобы полученную оценку можно было бы использовать на
практике она должна удовлетворять следующим условиям: 1) оценка должна быть не смещённой оценкой параметра, т.е. математическое
ожидание должно быть равно оцениваемому параметру. Если это условие не
выполняется, то оценку называют смещённой оценкой оцениваемого параметра; 2) оценка должна быть состоятельной оценкой оцениваемого
параметра; 3) Оценка должна быть эффективной оценкой оцениваемого
параметра; Из всех различных оценок выбираем ту которая имеет
наименьшую дисперсию она и называется эффективной если её дисперсия является
минимальной из всех получившихся дисперсий. Таким образом, чтобы полученная опытным путем оценка оцениваемого
параметра была пригодной она должна быть несмещённой состоятельной и
эффективной. Пусть изучается дискретная генеральная совокупность объема N количественного признака Х. Генеральной средней совокупностью называют среднее
Пусть для изучения генеральной совокупности относительно
некоторого количественного признака Х произведена выборка объема n.
Если же значение признака х1, х2,…. хk имеет соответственно частоты
xi ni 28×1+29×3+30×18+31×29+32×32+33×24+34×18+35×4+36×1 130 130 Выборочной дисперсией называется среднее
арифметическое квадратов отклонений наблюдаемых значений от выборочной средней.
Вычисляется выборочная дисперсия по формуле:
![]() 0, -∞<х≤28
0, -∞<х≤28

1
129/130
125/130
107/130
83/130
51/130
22/130
4/130
1/130
0
xi
28
29
30
31
32
33
34
35
36
Статистические оценки параметров распределения
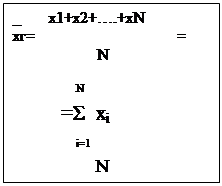
арифметическое наблюдаемых значений.
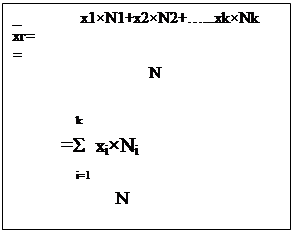
![]() Если же значение признака х1, х2,…….
хк имеют соответственно частоты N1,N2……. Nk, то
средняя генеральная вычисляется по формуле:
Если же значение признака х1, х2,…….
хк имеют соответственно частоты N1,N2……. Nk, то
средняя генеральная вычисляется по формуле:
![]()

Выборочной средней называют среднее арифметическое наблюдаемых значений
в данной выборке.
![]()
![]()
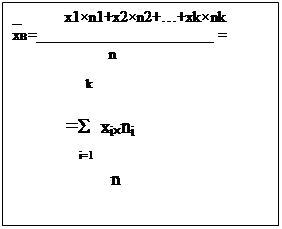
n1,n2,…. nk, то выборочная средняя определяется по формуле:
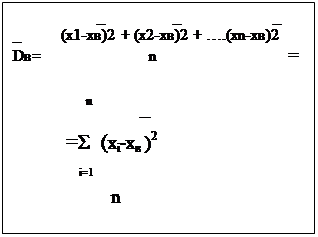
28
29
30
32
32
33
34
35
36
1
3
18
29
32
24
18
4
1
![]() хв =
хв = ![]() = 4158 = 31,98
= 4158 = 31,98
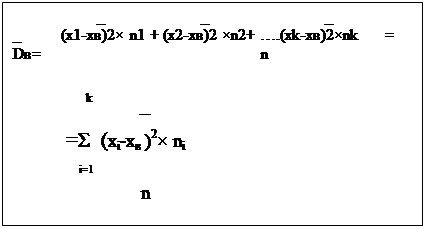
![]() Если же значение признака х1, х2….
x k имеет соответственно частоты n1,n2…. nk, то выборочная дисперсия вычисляется по формуле:
Если же значение признака х1, х2….
x k имеет соответственно частоты n1,n2…. nk, то выборочная дисперсия вычисляется по формуле:
![]()
(28-31,98) 2×1+ (29-31,98) 2×3+ (30-31,98) 2×18+ (31-31,98) 2×29+
Dв= + (32-31,98) 2×32+ (33-31,98) 2×24+ (34-31,98) 2×18+ (35-31,98) 2×
×4+ (36-31,98) 2×1 =
![]() 130
130
![]() = 291,972 = 2,24
= 291,972 = 2,24
130
Среднее выборочное квадратичное отклонение - это величина численно равная квадратному корню из выборочной дисперсии.
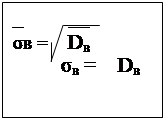 |
__
σв = √ 2,24 = 1,5
Нормальный закон распределения случайной величины
![]()
Говорят, что случайная величина распределена по нормальному закону если плотность распределения этой случайной величины выражается формулой:
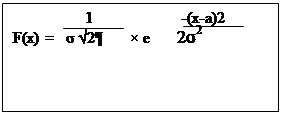 |
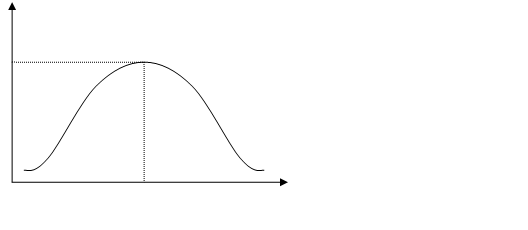
Проверка гипотезы о нормальном распределении изучаемой величины
Гипотезу Н0 выдвигаем в качестве основной - пусть наш исследуемый признак х распределён по нормальному закону. Параллельно гипотезе Н0 выдвигаем альтернативную гипотезу о том, что исследуемый признак распределен не по нормальному закону.
Проверка гипотезы о предполагаемом законе распределения производится с помощью специально подобранной величины называемой критерием согласия.
Для исследования воспользуемся критерием χ2 Пирсона.
Вычисляем χ2 для наблюдаемых значений. Для вычислений составляем таблицу и воспользуемся следующими формулами:

_
хв =31,98
_
Dв=2,24
_
σв=1,5
Таблица отдельный файл
k (ni-ni*)2
![]() χ2 набл.=Σ
χ2 набл.=Σ
i=1 ni
χ2 набл=13,8725515
Далее находим χ2 с помощью таблицы критических точек распределения по заданному уровню значимости £=0,05 и числу степеней свободы.
К=S-3
5-3=2
χ2крит. =6,0
χ2 набл=13,8725515 > χ2крит=6,0
Гипотеза не принимается.
Вывод
В данной работе был изучен статистический материал по исследованию прочности на разрыв полосок ситца, статистически были обработаны и получены соответствующие результаты.
Цель курсовой работы реализована через решение поставленных задач.
Наглядно представление о поведении случайной величины показано через полигон частот и полигон относительных частот, гистограммы частот и гистограммы относительных частот.
Была составлена и построена эмпирическая функция распределения и построен график этой функции на основе наблюдаемых значений.
0ценили параметры распределения:
выборочную среднюю
выборочную дисперсию
выборочное среднее квадратичное отклонение.
После обработки имеющихся статистических данных было выдвинуто предположение о нормальном распределении случайной величины. При проверке этой гипотезы оказалось, что случайная величина нераспределена по нормальному закону.
Литература
1. Гнеденко Б.В. Курс теории вероятностей: Учебник. - М.: Наука, 1988.
2. Боровков А.А. Теория вероятностей: Учеб. пособие.; М.: Наука, 1986.
3. Бочаров П.П., Печинкин А.В. Теория вероятностей: Учеб. пособие. - М.: Изд-во ун-та Дружбы народов, 1994.
4. Бочаров П.П., Печинкин А.В. Математическая статистика: Учеб. пособие. - М.: Изд-во ун-та Дружбы народов, 1994.
5. Б.М. Рудык, В.И. Ермаков, Р.К. Гринцевевичюс, Г.И. Бобрик, В.И. Матвеев, И.М. Гладких, Р.В. Сигитов, В.Г. Шершнев. Общий курс высшей математики для экономистов: Учебник / Под ред. В.И. Ермакова. - М.: ИНФАРМА-М, 2005. - 656с. - (Высшее образование).























 (zip - application/zip)
(zip - application/zip)










