Информатиканы

ОҢТҮСТІК ҚАЗАҚСТАН МЕМЛЕКЕТТІК

ПЕДАГОГИКАЛЫҚ ИНСТИТУТЫ

ФИЗИКА-МАТЕМЕТИКА ФАКУЛЬТЕТІ

ИНФОРМАТИКА КАФЕДРАСЫ

КУРСТЫҚ ЖҰМЫС

Информатиканың логикалық негіздері

           Пәні: Мәліметтер қоры және ақпаратты жүйелеу

Мамандығы: 5В011110- Информатика

Орындаған: Тухтамуратов С.

 

Қабылдаған: Әмірбекұлы А.

Комиссия мүшелері: Лесбаев А.У

ШЫМКЕНТ

2015ж

МАЗМҰНЫ

    Глоссарий.......................................................................
........................................3

КІРІСПЕ.........................................................................
........................................5

     1.ИНФОРМАТИКАНЫҢ ЛОГИКАЛЫҚ НЕГІЗДЕРІ.................................6

1.1  Логикалық қосу ................................................................................
...........9

1.2  Логикалық азайту..........................................................................
.............10

1.3 Логикалық көбейту.....................................................................
.................11

2. Информатиканы логикалық негіздерінің объектіге бағытталған түсінігі ................................................................................
..............................15

     2.1 Аты.............................................................................
.....................................15

     2.2 Өрісі......................................................................
...........................................17

     2.3 Қасиеті....................................................................
........................................19

     2.4 Әдісі......................................................................
...........................................21

ҚОРЫТЫНДЫ..................................................................
.................................3

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ..............................................3

Глоссарий

Мультимедиялық технологиялар -әртүрлі типті мәліметтерді дайындау, өңдеу, біріктіру, ұсыну әрекеттерін ақпараттық және бағдарламалық жабдықтарды пайдалану арқылы жүзеге асыратын құралдар, әдістер мен тәсілдер жиынтығы.

Java бағдарламасы - Sun Microsystems компаниясының технологиясы Internet базасына негізделген платформалық өңдеу бағдарламаларына қолданады.

javascript- Java бағдарламасына еш қандай қатысы жоқ. Бұл бағдардама клиенттік тарапынан берілген негізгі тілдердің бірі.

Қашықтан білім беру - жаңа ақпараттық технологияларды пайдалана отырып, істеп жүрген жұмысынан немесе оқудан қол үзбей білімді жетілдіру ісін жүзеге асыру деген мағананы білдіреді.

Гипермәтін– қосымша элементтерді басқару мақсатында ішіне арнаулы код, яғни екпінді элемент (anchor) орналасқан мәтін;

Internet –миллиондаған компьютерлерді бір алып желіге біріктіретін, ақпаратқа шексіз қол жеткізу және түрлі амалдармен қатынас жасау мүмкіндігін ұсынатын дүниежүзіндегі ең үлкен және ең танымал желі.Атрибуттар немесе сипаттамалар – тәг атауынан және бір-бірінен бос орын арқылы бөлініп жазылатын қосымша түйінді сөздерден тұрады.

Айнымалы конфигурациялар -Frontpage компоненттерінің тағы бір түрі қойылатын деп аталатын компоненттер (Substitution Component) бетке айнымалы конфигурацияның құрамын қосуға арналған.

Анықтауыш (definition) – туралаудың арнайы түрі, терминдер мен олардың түсіндірмелерінен тұратын тізімді беру үшін қолданылады.

Web-сервер – бұл Web–сайттар, мәліметтер қоры, сценарийлер және т.б. қажетті мәліметтер орналасатын компьютер

Серверлерді администрациялау -Сервер администраторы Frontpage (Frontpage Server Administrator) – Frontpage-пен бірге қолданылатын серверлік кеңейткіштерді орнату және алу операцияларын орындайтын бағдарлама болып табылады.

Мәлiметтер қоры– бiр- бiрiмен байланысқан мәлiметтердi, объектiлердi және МҚБЖ баптау (белгiлi бiр қалыпқа келтiру) параметрлерiн сақтайтын файлдар. Әдетте МҚБЖ кез-келген бiр мәселенi шешу жолында құрылады.

Мәлiметтер қорын басқару жүйелерi (МҚБЖ)– мәлiметтер қорымен жұмыс iстеуге арналған, оны басқару мен тҥрлендiрудi жҥзеге асыратын программалар тобы. Ағылшынша оларды DBMS(database manaqement system) деп атайды.

Кесте– мәлiметтер қорымен жұмыс iстеуге арналған негiзгi объект, мәлiметтер қоймасы.

Жазба– кестенiң бiр қатары, яғни жолы. Ол МҚБЖ мәлiметтерiн сақтайтын негiзгi блок болып болып табылады.

Өрiс– кестедегi бағана немесе тiк жол. ACCESS – те өрiс мәлiметтерiн сипаттайтын оның бiрсыпыра қасиеттерi болады.

Сұраныc– жұмыс iстеушi адамның керектi мәлiметтердi бiр немесе бiрнеше кестеден белгiлеген шарттарға байланысты таңдап алу тәсiлi. Таңдап алуға сұраныс беру арқылы есептелетiн өрiстерден немесе басқа кестеден алынған өрiстерден тұратын виртуалды сұранымдар құруға болады.

Форма– мәлiметтердi экранға бейнелеу жолы немесе оларды басқару мҥмкiндiктерi.

Басылым– мәлiметтердi баспаға шығарып, қағазда бейнелеу тәсiлi.

Түйiндi өрiс– кестедегi жазбаларды таңдап алу мақсатында мәндерi қолданылатын негiзгi iс.

Кiлт немесе түйiн– кесте жазбаларын анықтайтын немесе кестелер арасындағы байланысты ұйымдастыратын бiр немесе бiрнеше тҥйiндi өрiстер.

Санауыш– кестедегi жазбалардың реттiк нөмiрлерi орналасатын өрiс.

Индекс– индекстелетiн өрiс мәнi арқылы кесте жазбаларын автоматты тҥрде сұрыптау тәсілі.

Жазбаны белгілеу аймағы– кесте жолын белгілеуге мҥмкіндік беретін, оның сол жақ шетіндегі тіктөрбұрышты аймақ.

КІРІСПЕ

         Логикалық жалғаулықтар математикада күрделі айтылымдарды сипаттайтын логикалық операциялар болып табылады. Логикалық айтылымдармен жұмыс істеу үшін оларға ат қояды.
Әрбір логикалық жалғаулық логикалық айтылымдармен орындалатын операция ретінде қарастырылады және олардың өз аты мен белгіленуі болады. Математикалық логикада ЖӘНЕ, НЕМЕС, ЕМЕС логикалық операциялары ақиқаттық мәндер кестесімен анықталады.
Ақиқаттық кестесі – бұл логикалық операцияның кестелік түрде ұсынылуы, онда кірістік операндалардың ақиқаттық мәндерінің барлық мүмкін терулері осы терулердің әрқайсысына арналған опеарцияның шығыстық нәтижесінің ақиқаттық мәнімен бірге аталған.
Логикалық көбейту.ЖӘНЕ жалғаулығының көмегімен қарапайым екі А мен В айтылымдарының бір құрамдасқа бірігуі логикалық көбейту немесе конъюнкция, ал операцияның нәтижесі – логикалық көбейтінді деп аталады.
Логикалық қосу. НЕМЕСЕ логикалық операциясы белгісімен белгіленеді. НЕМЕСЕ логикалық операциясының ақиқаттық . Логикалық терістеу. ЕМЕС операциясы айтылымның үстіне сызықша салумен белгіленеді. ЕМЕС (терістеу) операциясының ақиқаттық кестесі.
Бұл операцияның ақиқаттық кестесінен, егер бастапқы А айтылымы жалған болса, онда А емес, теріске шығаруы иә мәніне ие болады. Және, кеісінше, егер бастапқы А айтылымы ақиқат болса, А емес, жоқ мәніне ие болады. Логикалық жалғаушылар математикалық логикада күрделі пайымдауларды сипаттайтын логикалық операциялар болып табылады. Математикалық логикада ЖӘНЕ, НЕМЕСЕ, ЕМЕС логикалық операциялары ақиқаттық мәндер кестесімен анықталады. ЖӘНЕ жалғаулығының көмегімен бір құрамдасқа екі қарапайым А және В пайымдауларының бірігуі логикалық көбейту немесе конъюнкция деп аталады, ал операцияның нәтижесі - логикалық көбейтінді. Мұндағы А және В - иә немесе жоқ мәнін қабылдай алатын екі пайым. Мысалы, деректері қарапайым айтылымдар болсын: А - "Астана - Қазақстанн астанасы", В - "Астанада 300 мыңнан астам адам тұрады". Онда осы айтылғандардың логикалық көбейтіндісі, немесе конъюнкциясы, күраіу пайымдау болады: Астана - Қазақстанның астанасы және Астанада 300 мыңі астам адам тұрады пайымдауларьшың ақиқат мәніне байланысты иә немесе жоқ мә қабылдайды. А мен В пайымдауы иә мәнін қабылдағанда "А мен В" кұрам пайымдауы да иә мәнін қабылдайтьшын кестеден көреміз. Пікірдің екеуі де ақиқат болғанда, А және В конъюнкциясы ақиқат; А немесе В пікірлерінің біреуі немесе екеуі де жалған болғанда, А және В конъюнкциясы жалған болатындығын көреміз.

1.ИНФОРМАТИКАНЫҢ ЛОГИКАЛЫҚ НЕГІЗДЕРІ

         Автоматикалық қондырғылар мен есептеу техникасы үшін логикалық амалдарды орындауға арналған қарапайым логикалық амалдардың қаншалықты маңызды екендігі бәрімізге белгілі. Бірақ сол элементтердің ішкі құрылымдарын жан-жақты түсіндіру , оларды өз бетінше қолмен жинау және іс жүзінде қолдану мәселелеріне дұрыс көңіл бөлінбейді. Қазіргі кезде логикалық элементтер тіркеуіштер (регистр), оперативті жады, процессор туралы ұғымдар, компьютердің оқу процесіне мейлінше енуіне байланысты әрбір шәкірттің алдынан үздіксіз туындауда.

        Әлбетте, логикалық амалдарды орындауға арналған элементтер тек логикалық шамалармен жұмыс істейді. Логикалық шамаларға шартты келісім бойынша кез келген процесті жатқызуға болады. Автоматикалық қондырғы – құрылымдар үшін , сыртқы бір әсердің болмау әсері, тізбектің ажырауы мен тұйықталуы , тізбекте электр ағысының жүру-жүрмеуі және т.б. құбылыстар – шартты түрде қабылданған логикалық процестер болып табылады. Бұл процестердің біреуі – тәуелсіз, екіншілері – тәуелді құбылыстар. Тәуелсіз құбылыстар мен шамалар аргумент деп , ал тәуелді шамалар функция деп аталады . Мысалы : тізбектің тұйықталуы мен сол тізбекте электр ағысының өтуі немесе ағыстың өтуі мен шамның жануы сондай құбылыстар.

       Математикалық символдарды қолдана отырып, аргументті – Х, функцияны – У арқылы белгілеу қабылданған, яғни У = f (Х).

       Есептеу техникасымен автоматикалық құрылымдар екілік есептеу жүйесінің негізі болатын 0 мен 1-ден тұратын сандармен жұмыс істейді. Осы шараларға жаңағы айтылған процестердің барлығын шартты келісім бойынша жатқыза беруге болады. Басқаша айтқанда, бір құбылыс – жалған, оның шартты мәні – «0». Оған қарсы екінші құбылыс – шыңдық (ақиқат), оның шартты мәні – «1».

     Сол секілді, жоғары деңгейдегі электрлік шаманы (потенциалды) – логикалық – «1», төменгі деңгейдегі потенциалды – логикалық – «0» деп бағалауға болады. Логикалық элементтер осы екілік есептеу жүйесінің аргументтері мен логикалық амалдарды орындау үшін қолданылады. Соған байланысты логикалық функцияда аргументтің мәні сияқты «0» мен «1» деп өзгеше шамаға ие болмайды.

     Өңделетін информация екілік санау жүйесінде берілетін электронды қондырғы логикалық элемент деп аталады. «Логика» термині электроникаға 0 мен 1 мәндерін қабылдайтын логика алгебрасынан келді.

     Екілік санау жүйесіндегі айнымалылар және оның функцияларын, логикалық айнымалылар және логикалық функциялар, ал осы функцияларды өңдейтін қондырғы логикалық немесе сандық қондырғы деп аталады.

    Іс жүзінде - кодтаудың барынша көп таралған тәсілдерінің бірінде - микросхемалар +5 В –ке дейінгі кернеу өндіретін қоректендіру көзі қосылады, 0-ден 0,5 В-ке дейінгі потенциалдық 0-ге, 2,5-тен 5 В-ке дейінгі потенциал 1-ге сәйкес келеді.

     Цифрлық есептеу техникасының тарихына тоқтала кетейік. Программаланатын автоматты есептеу машинасын жасаудың алғашқы идеясын 160 жыл бұрын ағылшын оқымыстысы Чарльз Беббидж ұсынды. Беббидж машинасының «элементтік базасы» ретінде бірнеше тісі бар «цифрлық» дөңгелектер алынған.

     Ағылшын философы және математигі Джорж Буль 1854 жылы қазіргі ЭВМ-дердің түп қазығының теориясы болып табылатын логика алгебрасын жасап шығарды. Бұл алгебраның негізіне тек екі мән қабылдайтын, мәселен: «иә» - «жоқ», «0» - «1»; «қосылған» - «қосылмаған» , т.б. кез келген айнымалы жатады. Буль алгебрасымен электрондық элементтердің екілік сипатының арасындағы терең де принципті байланысты атақты американ математигі Джон фон Нейман жасады. Нейман «ЕМЕС», «ЖӘНЕ», «НЕМЕСЕ» схемаларының көмегімен ЭВМ-нің негізгі жүйелерін жасауға болатынын дәлелдеді. Машинаның жұмысын математикалық түрде дәл мен дәл сипаттау және қасиеттері осындай сипаттау негізінде алдын-ала белгіленген машинаның жақсартылған түрін құру конструкторларды әр уақытта ынталандырған болатын. Бұл сияқты формальдау сипаттау кезінде әдетте бір қатар математикалық пәндер пайдаланылады. ЭЕМ жасаушыларының машина жұмысын талдауда және оның тораптарын құрастыруда Буль алгебрасы баға жетпес көмек көрсетті.

     Буль алгебрасының бастапқы ұғымы – пікір. Пікір деп тек қана ақиқаттық тұрғыдан бағаланатын кез келген тұжырым түсіндіріледі. Пікірдің әділетті, мазмұнды, дөрекі, жақсы деген сияқты сапалық сипаттамалары қарастырылмайды. Буль алгебрасы тұрғысынан қарағанда пікірдің ақиқат немесе жалған болуы мүмкін.

      Мысалы: Х = « Саты ауылы Райымбек ауданының құрамына кіреді».

                        У = « Шелек өзені Жалаңаш ауылы арқылы өтеді» деген пікірдің біріншісі - ақиқат, екіншісі - жалған. Бұған қоса, пікірлер, шын мәнінде, оның ақиқат жағдайында 1 мәнін, ал пікір жалған болғанда 0 мәнін қабылдайтын Буль алгебрасының айнымалылары болып келеді.  Мұндай айнымалыларды логикалық айнымалылар (немесе Буль айнымалылары) деп атайды. Демек, келтірілген мысалдағы екі пікірді былай да жазуға болады: Х = 1; У = 0.

      Пікірлер қарапайым және күрделі болуы мүмкін. Пікірдің мәні қандай да болсын басқа бір пікірлердің мәндеріне тәуелсіз болса, ол қарапайым пікір деп аталады. Ақиқаттық мәні басқа пікірлердің мәндері арқылы анықталатын пікір күрделі пікір болып саналады. Кез келген күрделі пікір кейбір екілік аргументтердің, яғни қарапайым пікірлердің логикалық функциясы болып табылады. Қарапайым логикалық пікірлерді қарастырайық.

      Олардың көмегімен қарапайым пікірлерден күрделі пікір құрастыруға болатын сияқты ЭЕМ-нің тораптары мен блоктары құрылады. Элементар пікір деп басқа пікірлерге жіктеуге келмейтін пікірді айтамыз. Егер пікірді басқа пікірлерге жіктеуге болатын болса, онда оны құрама пікір деп атайды. Мысалы, пікір: С: « 5 > 2» - элементар, ал пікір D: « 5 > 2» және « 5 – тақ сан» -құрама болады, өйткені ол екі пікірден: бірі «5 > 2» , ал екіншісі « 5 – тақ сан» деген пікірлерден құралады.

     Құрама пікірлер әр түрлі жалғаулықтар және сөз тіркестері арқылы элементар пікірлерден құралады. Мысалы: қарастырылған D пікірі «және» жалғаулығы арқылы элементар пікірлерден құралған. Ал мына «берілген төртбұрыш - ромб немесе квадрат» деген пікір «берілген төртбұрыш - ромб» деген және «берілген төртбұрыш - квадрат» деген екі пікірден «немесе» деген жалғаулық арқылы құралып тұр.

    Құрама пікірді «егер . . ., онда ...», «сонда және тек сонда» деген сөздерді пайдаланып та алуға болады.

     Мысалы: « Егер үшбұрыш тең қабырғалы болса, онда ол тең бүйірлі», «төртбұрыштың диагональдары қиылысу нүктесінде қақ бөлінетін болса, сонда және тек сонда ғана ол төртбұрыш параллелограмм болады».

     Грамматикада «және», «немесе», «егер ..., онда ...», «сонда және тек сонда» және осыларға ұқсас айтылуларды байлам, жалғаулық деп атайды. Логикада оларды сөйлемдер арасындағы байламдар деп атайды, өйткені мұндай жалғаулықтар екі пікірді бір құрама пікірге біріктіреді.

    Сөйлем арасында қолданылатын тағы бір « ... дұрыс емес» дейтін тіркесті қарастырайық. Ондай тіркес қандай да пікірді теріске (жоққа) шығару мақсатында қолданылады. «Біз жазда саяхатқа барамыз дегеніміз дұрыс емес» деген сөйлем «Біз жазда саяхатқа барамыз» деген сөйлемді теріске шығарады. Сөйлем арасында « ... дұрыс емес» тіркесін қоссақ, онда біз жаңа сөйлем аламыз. Сонымен « ... дұрыс емес» тіркесі қандай да бір екі сөйлемді бір сөйлемге байланыстырмағанымен оны логикада байлам деп санайды.

    Сонымен «және», «немесе», « ... дұрыс емес», «егер ..., онда ...», « сонда және тек сонда», т.б. байламдар арқылы кез келген элементар пікірлерден әр түрлі пікірлер алынады, әрі олардың мағыналық характеристикасы қаралмайды.

    Мысалы: «Жер Айдан үлкен және киттер суда өмір сүреді», «Бүгін мен театрға барамын» немесе « Жайық өзені Арал теңізіне құяды» және т.с.с. пікірлердің айтылуы мүмкін. Пікірлер теориясында құрама пікірлерге кіретін элементар пікірлердің шын немесе жалған екендігіне байланысты құрама пікірдің өзінің шын немесе жалған екендігі зерттеледі.

Берілгендер қорының жазбасын ЭЕМ жадында қарастырудың тағы бір әдәсі - әрбір жазбаның аргументтерінің бірі келесі жазбаны көрсететін рекурсивті құрылымды қолдану болып табылады. Мұндай құрылымды пайдалану басқа көрсеткіштің өңдеу әрекеттерінің барлығын өзі орындайды.

Келесі жазбаның жоқ екендігін көрсететін соңғы жазба көрсеткіші үшін қосымша аргумент негізінде «еnd» енгізіледі.

Жұмысшы (аты, бөлім, қызметі, айлық келесі жазбаны көрсеткіш) сызықты рекурсивті құрылымын қарастырайық. Мұнда құрылымының қосымша аргументі берілгендер қорының келесі жазбасын нұсқайды, өзі осы жазба құрылымда жазылған. Яғни, жазба құрылымы өзін-өзі арқылы анықтайды.

. Екінші ереже рекурсивті құрылымның жоғарғы дәрежесін елемейді және берілгендер қорының қалған бөлігінің информациялық элементтің бүтінділігін алады.

  1.1   Логикалық қосу

Логикалық қосу (дизъюнкция): Екі немесе оданда кӛп пікірлерді «немесе» жалғаулығы кӛмегімен біріктіру амалы логикалық қосу немесе дизъюнкция деп аталады. Дизъюнкция латынның discnctio ажыратамын деген сӛзінен шыққан. - табиғи тілде «немесе» жалғаулығына сәйкес келеді; - пікірлер алгебрасында v белгісімен белгіленеді; Дизъюнкция – ол әрбір қарапайым екі пікірге, пікірлердің екеуі де жалған болғанда ғана жалған мән қабылдайтын, пікірлердің ең болмағанда біреуі ақиқат болғанда ақиқат мән қабылдайтын күрделі пікірді сәйкес қоятын логикалық амал. Жиындар алгебрасында дизъюнкцияға жиындардың бірігу амалы, яғни АvВ жиындарын қосу нәтижесінде алынған жиынға не А, не В жиындарының бірінде жататын элементтерден тұратын жиын сәйкес келеді. Логикалық қосу функцияның ақиқаттық кестесі мен графикалық бейнеленуі Ақиқаттық кестесі А В АvВ 0 0 0 0 1 1 1 0 1 1 1 1 Логикалық қосу амалының кӛмегімен құрылған бұл пікірде тек бірінші пікір жалған, себебі соңғы үш құрмалас пікірлердің әрқайсысында ең болмағанда бір қарапайым пікір ақиқат. Логикалық теріске шығару (инверсия) «Емес» жалғаулығының кӛмегімен пікірді теріске шығару амалы логикалық теріске шығару немесе инверсия д. а. - табиғи тілде «дұрыс емес», «теріске шығару» сӛздеріне және «емес» жалғаулығына сәйкес келеді; - пікірлер алгебрасында А белгісімен белгіленеді; Инверсия – ол әрбір қарапайым пікірлерге, негізгі пікірдің жалған екенін қорытындылайтын күрделі пікірді сәйкес қояты логикалық амал. Жиындар алгебрасында логикалық теріске шығару амалына әмбебп жиынға дейін толықтауыш амалы сәйкес келеді, яғни А жиынын теріске шығару нәтижесінде оған А жиынынажатпайтын элементтерден құралғанА жиынға сәйкес келеді. Біріктіруші мағынада қолданылатын НЕМЕСЕ жалғаулығының көмегімен қарапайым Ажәне В айтылымдарының бір құрамдасқа бірігуі логикалық қосу немесе дизъюнкция(латынша disjuncnctio – бөлу), ал операцияның нәтижесі – логикалыққосынды депаталады. НЕМЕСЕ логикалық операциясы белгісімен (кейде + белгісімен белгіленеді). А немесе В пікірлерінің ең болмағанда біреуі ақиқат болғанда, А немесе В дизъюнкциясы ақиқат. А және В пікірлерінің екеуі де жалған болғанда, А және В дизъюнкциясы жалған. Осындай операцияларға логикалық қосу — """дизъюнкция""" (“немесе”), көбейту — """конъюнкция""" (“және”), терістеу — """инвертирлеу""" (“емес”) жатады. Қарапайым Логикалық элементтердің шартты белгілері суретте көрсетілген. Ақпараттық сигналдар ретінде электр кернеуі немесе тогының дискреттік мәндері (деңгейлері) қолданылады. Мысалы:

·                    0 — төмен деңгейге, 1 — жоғары деңгейге сәйкес келеді.

Логикалық элементтер функционалдық белгіленуі, ақпарат беру әдісі, сұлбатех. шешімі және пайдаланылатын электрондық құралдары бойынша ажыратылады. Күрделі Логикалық элементтер қарапайым операциялар орындайтын элементтерді біріктіру арқылы жасалады. Мысалы:

·                    “немесе” — “емес”, “және — емес”, “немесе — және — емес”, т.б.

Құрылымдық түрде Логикалық элементтер жекеленген (дискретті) құраушылардан немесе интегралдық сұлба шала өткізгіш,[  (ИС) түрінде гибридті, үлдірлі орындалуы мүмкін. Қазіргі дербес компьютерлерде жоғары дәрежелі интеграциясы бар ИС-дағы Логикалық элементтер жүйелері қолданылады. Логикалық элементтер компьютерлердің, цифрлық автоматтардың элементтік негізін қалайды.](пленкалы), т.б.

         1.2 Логикалық азайту

Азайту — негізгі төрт арифметикалық амалдардыӊ бірі, қосу амалына кері амал сандардыӊ айырымын анықтайды, «−» таӊбасымен белгіленеді. Екі қосылғыштың берілген қосындысы мен осы қосылғыштың біреуі бойынша екінші қосылғышты анықтауға арналған. Берілген қосынды азайғыш, берілген қосылғыш азайтқыш, ал амал нәтижесі айырым деп аталады.

Берілген a санның (яғни азайғышты) b санға (яғни азайтқышқа) азайту нәтижесінде x саны (яғни екі санныӊ айырымы) пайда болады. Азайту амалы орындалған өрнек былайша жазылады:

x = a — b,

a — азайғыш,

b — азайтқыш,

x — екі санныӊ айырымы.

Азайту амалының нәтижесі: x — екі санныӊ айырымы деп аталады. Азайту амалына барлық сан аймағында (облысында) шектеу жоқ, бір мәнді орындалады.

Азайту амалын теріс сандары бар қосу амалыныӊ бір түрі деп есептесек болады. Мысалы,

5-2=3 амалды

5 және -2 қосындысы десек болады, яғни

5-2 өренгі 5+(-2) өрнегіне тепетеӊ .

Қосу амалын «—» ("минус") таңбасымен белгілеуді 1489 жылы чех математигі Ян Видман ұсынған.

1.3 Логикалық көбейту

Логикалық көбейту: Екі немесе одан да кӛп пікірлердің «және»жалғаулығы кӛмегімен біріктіру амалы логикалық көбейту немесе конъюнкция деп аталады. Конъюнкция латынның conjunction байланыстырамын деген сӛзінен шыққан. Табиғи тілде - «және» жалғаулығына сәйкес келеді. Пікірлер алгебрасында - ^ белгісімен белгіленеді. Конъюнкция –ол әрбір қарапайым екі пікірге, пікірлердің екеуі де ақиқат болғанда ғана ақиқат мін қабылдайтын күрделі пікірді сәйкес қоятын логикалық амал. Логикалық көбейту функцияның ақиқаттық кестесі мен графикалық бейнеленуі Ақиқаттық кестесі А В А^В 0 0 0 0 1 0 1 0 0 1 1 1 Логикалық кӛбейту амалымен құрылған бұл пікірде тек тӛртінші пікір ақиқат, себебі алғашқы үш құрама пікірдің әрқайсысында ең болмағанда бір қарапайым пікір жалған. Логикалық көбейту операциясы, логикалық "және",конъюнкция (Операция логическое умножение, логическое ( конъюнкция; logical multiplication, logical “and”, conjunction) — 1) егер екі операнд та «ақиқат мәнін қабылдайтын болса, онда нәтижесі “ақиқат”)(, ал қалған жагдайлардың барлығында жалған болатын екі орынды логикалық операция. Программалау тілдерінде AND, & және т.б. символдармен белгіленеді. Логикалық өрнектерді жазуға пайдаланылады; 2) тек екі аргументінің де мәні ақиқат болған кезде ғана мәні “ақиқат”( болатын екі айнымалының буль функциясы. Логикалық көбейту операциясына барабар.

Логикалық теріске шығару функциясының ақиқаттық кестесі Ақиқаттық кестесі Пікір: Бүгін информатикадан ашық сабақ болды Терістеу: Бүгін информатикадан ашық сабақ болғ ан жоқ Пікір: Бүгін информатикадан ашық сабақ болды Терістеу: Бүгін информатикадан ашық сабақ болғ ан жоқ Пікір: Бүгін информатикадан ашық сабақ болды Терістеу: Бүгін информатикадан ашық сабақ болғ ан жоқ Пікір: Терістеу: Теріске шығару функциясының мынандай қасиеттері бар: 1. Кез келген А аргументінің екі рет теріске шығарылуы сол аргументтің ӛзіне тең, А=A=A. 2. Қандай да бір логикалық теңдік бар болса, оның екі жағын да теріске шығару бұл теңдікті бұзбайды: яғни A1=A2 A1=A2. Құрама пікірлерді элементар пікірлерден «... егер..., онда...» сӛздер арқылы болатыны белгілі. Мысалы, «Егер мен билет сатып алсам, онда театрға барамын. Егер құрама пікірлерді құрайтын элементар пікірлерді А және В арқылы белгілесек, онда олардың барлығы да « егер А, онда В» түріндегі бірдей формада болады. «Егер А, онда В» түріндегі пікір, А, В пікірлерінің импликациясы латынша байланыстырамын деген сӛз деп аталады.

     Логика ұғымы объективті дүниенің, шындықтың даму заңдылықтарын бейнелеу мағынасында да қолданылады. Кең мағынада логика ойлаудың ғана емес, болмыстың да байланыстарын көрсетеді, бұл жағынан ол онтологиямен сабақтас. Ойлау мен таным қатар жүретіндіктен логика таным теориясымен (гносеологиямен) байланысады. логика философияның негізгі бөлігі болып табылады, өйткені философия “оймен басталып, оймен жалғасады, сондықтан оны кейде “ойлау туралы ойлау” деп анықтайды.

Логика тарихы философия тарихымен тығыз байланысты. логиканың алғашқы тарихи нұсқасын б.з.б. 4 ғасырда ежелгі грек философы Аристотель жасаған. Олдедуктивтік ой қорытулар теориясын (яғни силлогистиканы) қалыптастырып, логика қателердің алғашқы жіктелімін жасап берді және логикалық дәлелдеу туралы ілімнің негізін қалады. Дәстүр бойынша Аристотельдің логикасы — аподейктика — анық, ақиқат білім туралы ілім, ол Аристотельдің “Аналитикасында” баяндалған.

Аристотель дедуктивтік-силлогистік ілімді дамытса, Эпикур мен оның ізбасарлары индуктивтік логиканың бастауын ашып, индуктивтік жалпылаудың бірқатар ережелерін тұжырымдаған. Аристотельдің логикалық идеяларының сақталуына, олардың мән-маңызының ашылуы мен тарихи жалғасын табуына ортағасырлық ислам философтары әл-Кинди, әл-Фараби, ибн Сина, ибн Рушдтың сіңірген еңбегі зор. Аристотельдің дәлелденбейтін пікір, индукция туралы ілімін әл-Фараби жүйелі түрде дамытты. Ол предикат түрінде “өмір сүретін” құбылыстың бары жайында мүлде жаңа мәселе қойып, шартты силлогизм теориясын егжей-тегжейлі талдады, сөйтіп, логикадағы диалектикалық мәселелерді түсінуге елеулі үлес қосты.

Неміс философы Кант Аристотельге қарсы философияның зерттейтін формаларының деректік мәні жоқ, олар әншейінгі бос форма болып табылады, сондықтан, олардың мазмұн мен ақиқатқа қатысы жоқ деген пікір айтты. Кант пікірі бойынша, жалпы логика ғылымның формасын ғана емес, оның мазмұны мен генезисін де зерттейді. Жалпы логиканың ең жоғарғы принципі — қайшылық принципі (немесе қайшылыққа жол бермеу принципі), ал трансцендентальді логиканікі — әр түрлі пікірді біріктіріп, қисындастыру синтезі. Гегель “рухтың” тарихы, яғни мәдениет тарихы логикада синтезделуге тиіс, логика бұрынғы философияның, ең алдымен, онтологияның орнын басады, сонда болмыс пен ойлаудың тепе-теңдігі пікірдің дамуын, оның өз бетімен дамуының ішкі ырғағына сәйкес имманентті, диалекттка түрде болатынын дәлелдейді.

17 ғасырда Бэкон тәжірибеге сүйенген ғылымның басты құралы ретінде индуктивтік әдісті негіздеп, индуктивтік логиканың негізін саралап, силлогист. ілімді сынға алды. Декарт керісінше дедуктивтік әдіс пен дедуктивтік логиканы жоғары бағалап, ақиқатты дәлелдеудің басты жолы деп есептеді. Формальді логиканың әрі қарай дамуына аса зор үлес қосқан философтардың бірі — Лейбниц. Ол Аристотель категорияларын талдау арқылы ең қарапайым бастапқы ұғымдар мен пікірлерді іріктеп алып, адам ойының әліпбиін” құрастыру идеясын ұсынды, математика логиканың негізін қалады. Дж.С. Милльдің индуктивті ой қорыту теориясы ықтималдық теориясы мен логика алгебрасының қалыптасуына байланысты 19 — 20 ғ-ларда логиканың зерттеу саласына айналды. Бұл кезеңде индуктивтік логикамен дедуктивтік-математика логика дамыды. Дж.Буль, О де Морган және неміс математиктері Э.Шредер,П.С. Порец, т.б. математика әдістерді логикаға қолданудың нәтижесінде осы заманғы логика алгебрасы қалыптасты.

логикалық сөйлемдерді геометрия фигуралар арқылы түсіндіру әдісі И.Г. Ламберг және Б.Больцано еңбектерінде кездеседі. Сөйтіп, логикалық мәселелерді шешуде математика әдістерді қолдану кеңінен таралды. Қазақстанда математика логиканың дамуына академия А.Д. Тайманов зор үлес қосты. Ол логиканың ойлау формаларын (ұғым, пікір, ой-қорытынды) зерттеп, олардың мәнін, түрлерін, арақатынастарын, олармен операциялар жасаудың тәртібін ашып, оларға тән ережелер мен түпкілікті ойлау заңдарын саралады. Формальді логиканың (қазіргі логика) символик. (немесе математика логика) саласы дәстүрлі логиканың тарихи сабақтасы болып саналады. Мұнда дәстүрлі логиканың қойған мәселелерін шешу үшін символдар тілі, математика әдістер, логикалық есептеулер қолданылады. Бұлайша қарастыру ойлаудың жаңа заңдылықтарын ашуға, ойлау процесін автоматтандыруға, сөйтіп, осыған негізделген жаңа техника мен технологияны жасауға жағдай жасайды. Қазіргі кезде логика, негізінен, үш бөлімнен (пайымдаулар теориясы, математика және логикалық методология) тұратын, жан-жақты тармақталған ғылымға айналды. Тұтас алғанда, мұндағы зерттеулер тіл мен ойдың арақатынасының қай қырынан келетіне байланысты логикалық семиотика мен логикалық семантика тұрғысынан жүргізіледі. логикалық семиотикада тіл байламдары таңбалық объектілер ретінде қарастырылса, логикалық семантикада тіл мен логикалық теориялар олардың мазмұны жағынан зерделенеді.

Қазіргі логикада түсініктеме (интерпретация) ұғымы маңызды рөл атқарады, өйткені бұл ұғым арқылы логикалық заң және логикалық жалғасу ұғымдары анықталады. Кейінгі кездері логикалық зерттеулерде жаңа математика аппарат — категориялар теориясының тілі кеңінен қолданылуда. логикалық теориялар оларда зерделенетін логикалық лебіздердің сипатына, түптеп келгенде заттар қатынастарының түріне орай классик. және бейклассиктер болып бөлінеді. Қазіргі логиканың маңызды бір бөлігі — металогикада Логикалық теориялардың қасиеттері (қайшылықсыздығы, толықтығы, түпкілікті дедуктивтік принциптерінің тәуелсіздігі, т.б.) зерттеледі, яғни оны Логиканың өз түзілістері турасындағы өзіндік рефлексиясы деп атауға болады.

логикалық методолдар да қазіргі логиканың бір бөлігін құрайды. Оны жалпы (яғни, ғылым білімнің барлық салаларында қолданылатын танымдық амалдарды зерттейтін) және жекелеген ғылымдардың методологиясы (дедуктивтік ғылымдардың методологиясы, эмпирик. ғылымдардың методологиясы, әлеуметтік және гуманитарлық білімнің методологиясы) деп бөледі. логикалық-методолдар ізденістерде, әсіресе дедуктивтік ғылымдар методологиясы саласындағы жетістіктерді атауға болады (логиканың дедуктивтік теория ретінде құрылуы, математиканы негіздеу, білімді аксиоматизациялау және формальдандыру әдістерінің қолдау табуы, т.б.).

Қазіргі кезде эмпирик. ғылымдар методологиясының логикалық проблематикасы да (мысалы, гипотеза түзу және тексеру процесі, білімнің эмпирик. және теория деңгейлерінің арақатынасы, эмпирик. теориялардың Л-лық құрылымы, т.б.) белсенді зерттеліп келеді.

1.    Информатиканы логикалық негіздерінің объектіге бағытталған түсінігі

                                                     2.1 Аты

        Информатиканың  логикалық  негізі–адамның ойлауын формальдандыру, информатикалық технологияны интеллектендіру. Интелектуальды іс-әрекеттерді орындауға арналған ыңғайлы программа құру үшін математикалық логика заңдары мен принциптеріне негізделіп дайындалған . Компьютердің логикалық элементі – элементар (қарапайым) логикалық функцияны жүзеге асыратын электрондық логикалық схеманың бір бөлігі.

Компьютердің логикалық элементтері дегеніміз – ЖӘНЕ, НЕМЕСЕ, ЕМЕС электрондық схемалары және триггер.

Триггер дегеніміз – бұл компьютердің регистрлерінде екілік кодтың бір разрядын жадыда сенімді сақтау үшін кеңінен қолданылатын электрондық схема.

Бұл схемалардың көмегімен компьютер құрылғыларының жұмысын сипаттайтын кез келген  логикалық функцияны жүзеге асыруға болады. Әдетте, вентильдердің екіден сегізге дейін кірісі және бір немесе екі шығысы болады.

Вентильдердегі «1» және «0»  болатын екі логикалық жағдайды көрсету үшін оларға кірістік және шығыстық сигналдарында кернеудің белгіленген екі деңгейінің бірі сәйкес болады. Әдетте, жоғары деңгей – «ақиқат» (1) мәніне, ал төмен деңгей – «жалған» мәніне (0) сәйкес болады.

Әрбір логикалық элементтің өзінің логикалық функциясын көрсететін шартты белгісі болады.

Логикалық элементтердің жұмысын ақиқат кестелердің көмегімен сипаттайды.

у

х

х ˄ у

&

ЖӘНЕ схемасының  ақиқаттық кестесі                            ЖӘНЕ схемасы 

х	у	х˄у
0	0	0
0	1	0
1	0	0
1	1	1

НЕМЕСЕ схемасының  ақиқаттық кестесі                            НЕМЕСЕ схемасы 

х

у

х ˅ у

1

х	у	х˅у
0	0	0
0	1	1
1	0	1
1	1	1

ЕМЕС схемасының  ақиқаттық кестесі                           ЕМЕС схемасы 

х
1	0
0	1

х

Логикалық айнымалы мен кесте арасындағы байланысты көрейік:

х	у	z
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

Логикалық айнымалы саны-3 Жол саны – 23=8

х	у
0	0
0	1
1	0
1	1

Логикалық айнымалы саны-2 Жол саны – 22=4

1.2   Өрісі

  ЭЕМ қатысуымен шешілетін есептердің ішінде, әдетте логикалық деп аталатын есептер де аз емес. Логика- бұл адам ойлауының түрлері мен заңдары туралы, оның ішінде дәлелдеуге болатын пікірлердің заңдылықтары туралы ғылым.

  Ғылыми пән ретінде логиканың формальды, математикалық ықтималдықты логика  және т.б. түрлері қалыптасқан.

Формальды логика сөйлеу тілімен білдіретін біздің кәдімгі мазмұнды пікірімізді талдаумен байланысты.

 Ықтималдық логика – кездейсоқ параметрлермен  жасалатын сынақтың бірнеше серияларын қолдануға негізделген.

 Математикалық логика формальды логиканың бөлігі болып табылады және оның дәлме дәл анықталған обьектілері мен пікірлері бар, олардың ақиқаттығын немесе жалғандығын бір мәнді шешуге болатын ойларды ғана зерттейді.

 Математикалық логиканың саласы пікірлер алгебрасы ретінде (оның басқаша  логика алгебрасы деп атайды, ол алғаш рет 19 ғасырдың ортасында ағылшын математигі Джордж Бульдің еңбектерінде пайда болды. Бұл - дәстүрлі логикалық есептерді алгебралық әдістермен шешуге талаптанудың нәтижесі), информатикада жақсы меңгерілген.

        Логика алгебрасының математикалық аппараты компьютердің аппараттық құралдарының жұмысын сипаттауға өте қолайлы, өйткені компьютердегі екілік санау жүйесі болып табылады, өздерін білесіңдер, онда екі цифр:  0 мен 1 қолданылады, ал логикалық айнымалылардың мәндері де 2:   0 және 1.

Пікір дегеніміз – жалған немесе ақиқат болуы мүмкін қандай да бір пайымдау. Мысалы, 

«Қара –ақ», «2*2=4» деген ақиқат, ал «тау тегіс », «2*2=5» деген –жалған пікірлер.

Егер пікір айтылған ой обьектілерінің кез келгені үшін рас болса, онда жалпы пікір тепе тең ақиқат деп аталады. Мысалы, «иттің төрт аяғы бар» пікірі кез келген ит үшін рас.

Күрделі жағдайларда сұрақтардың жауабы ЖӘНЕ, НЕМЕСЕ, ЕМЕС логикалық жалғаулықтарын пайдаланып, құрамды пікірелер арқылы беріледі.

Логикалық жалғаулықтардың көмегімен  басқа пікірлерден құрастырылған пікірлерді құрамды деп атайды. Құрамды емес пікірлерді қарапайым немесе элементар деп атайды.

Құрамды пікірдегі ЖӘНЕ жалғаулығы әрқашан құраушы пікірлердің бәрін ақиқат деп ұйғарады.

Барлық компьютерлік бағдарламада және математикалық пайымдауда немесе жалғаулығы тек біріктіруші ролде түсініледі. Мысалы:  х=0 немесе у=0 пайымдауындағы немесе жалғаулығы не у=0 не х=0,  у=0 және  х=0 дегенді білдіреді.

ЕМЕС жалғаулығы теріске шығаруды тұжырымдау үшін қолданылады.

2.3 Қасиеті

         Автоматикалық қондырғылар мен есептеу техникасы үшін логикалық амалдарды орындауға арналған қарапайым логикалық амалдардың қаншалықты маңызды екендігі бәрімізге белгілі. Бірақ сол элементтердің ішкі құрылымдарын жан-жақты түсіндіру , оларды өз бетінше қолмен жинау және іс жүзінде қолдану мәселелеріне дұрыс көңіл бөлінбейді. Қазіргі кезде логикалық элементтер тіркеуіштер (регистр), оперативті жады, процессор туралы ұғымдар, компьютердің оқу процесіне мейлінше енуіне байланысты әрбір шәкірттің алдынан үздіксіз туындауда.

        Әлбетте, логикалық амалдарды орындауға арналған элементтер тек логикалық шамалармен жұмыс істейді. Логикалық шамаларға шартты келісім бойынша кез келген процесті жатқызуға болады. Автоматикалық қондырғы – құрылымдар үшін , сыртқы бір әсердің болмау әсері, тізбектің ажырауы мен тұйықталуы , тізбекте электр ағысының жүру-жүрмеуі және т.б. құбылыстар – шартты түрде қабылданған логикалық процестер болып табылады. Бұл процестердің біреуі – тәуелсіз, екіншілері – тәуелді құбылыстар. Тәуелсіз құбылыстар мен шамалар аргумент деп , ал тәуелді шамалар функция деп аталады . Мысалы : тізбектің тұйықталуы мен сол тізбекте электр ағысының өтуі немесе ағыстың өтуі мен шамның жануы сондай құбылыстар.

       Математикалық символдарды қолдана отырып, аргументті – Х, функцияны – У арқылы белгілеу қабылданған, яғни У = f (Х).

       Есептеу техникасымен автоматикалық құрылымдар екілік есептеу жүйесінің негізі болатын 0 мен 1-ден тұратын сандармен жұмыс істейді. Осы шараларға жаңағы айтылған процестердің барлығын шартты келісім бойынша жатқыза беруге болады. Басқаша айтқанда, бір құбылыс – жалған, оның шартты мәні – «0». Оған қарсы екінші құбылыс – шыңдық (ақиқат), оның шартты мәні – «1».

     Сол секілді, жоғары деңгейдегі электрлік шаманы (потенциалды) – логикалық – «1», төменгі деңгейдегі потенциалды – логикалық – «0» деп бағалауға болады. Логикалық элементтер осы екілік есептеу жүйесінің аргументтері мен логикалық амалдарды орындау үшін қолданылады. Соған байланысты логикалық функцияда аргументтің мәні сияқты «0» мен «1» деп өзгеше шамаға ие болмайды.

     Өңделетін информация екілік санау жүйесінде берілетін электронды қондырғы логикалық элемент деп аталады. «Логика» термині электроникаға 0 мен 1 мәндерін қабылдайтын логика алгебрасынан келді.

     Екілік санау жүйесіндегі айнымалылар және оның функцияларын, логикалық айнымалылар және логикалық функциялар, ал осы функцияларды өңдейтін қондырғы логикалық немесе сандық қондырғы деп аталады.

    Іс жүзінде - кодтаудың барынша көп таралған тәсілдерінің бірінде - микросхемалар +5 В –ке дейінгі кернеу өндіретін қоректендіру көзі қосылады, 0-ден 0,5 В-ке дейінгі потенциалдық 0-ге, 2,5-тен 5 В-ке дейінгі потенциал 1-ге сәйкес келеді.

     Цифрлық есептеу техникасының тарихына тоқтала кетейік. Программаланатын автоматты есептеу машинасын жасаудың алғашқы идеясын 160 жыл бұрын ағылшын оқымыстысы Чарльз Беббидж ұсынды. Беббидж машинасының «элементтік базасы» ретінде бірнеше тісі бар «цифрлық» дөңгелектер алынған.

     Ағылшын философы және математигі Джорж Буль 1854 жылы қазіргі ЭВМ-дердің түп қазығының теориясы болып табылатын логика алгебрасын жасап шығарды. Бұл алгебраның негізіне тек екі мән қабылдайтын, мәселен: «иә» - «жоқ», «0» - «1»; «қосылған» - «қосылмаған» , т.б. кез келген айнымалы жатады. Буль алгебрасымен электрондық элементтердің екілік сипатының арасындағы терең де принципті байланысты атақты американ математигі Джон фон Нейман жасады. Нейман «ЕМЕС», «ЖӘНЕ», «НЕМЕСЕ» схемаларының көмегімен ЭВМ-нің негізгі жүйелерін жасауға болатынын дәлелдеді. Машинаның жұмысын математикалық түрде дәл мен дәл сипаттау және қасиеттері осындай сипаттау негізінде алдын-ала белгіленген машинаның жақсартылған түрін құру конструкторларды әр уақытта ынталандырған болатын. Бұл сияқты формальдау сипаттау кезінде әдетте бір қатар математикалық пәндер пайдаланылады. ЭЕМ жасаушыларының машина жұмысын талдауда және оның тораптарын құрастыруда Буль алгебрасы баға жетпес көмек көрсетті.

     Буль алгебрасының бастапқы ұғымы – пікір. Пікір деп тек қана ақиқаттық тұрғыдан бағаланатын кез келген тұжырым түсіндіріледі. Пікірдің әділетті, мазмұнды, дөрекі, жақсы деген сияқты сапалық сипаттамалары қарастырылмайды. Буль алгебрасы тұрғысынан қарағанда пікірдің ақиқат немесе жалған болуы мүмкін.

      Мысалы: Х = « Саты ауылы Райымбек ауданының құрамына кіреді».

                        У = « Шелек өзені Жалаңаш ауылы арқылы өтеді» деген пікірдің біріншісі - ақиқат, екіншісі - жалған. Бұған қоса, пікірлер, шын мәнінде, оның ақиқат жағдайында 1 мәнін, ал пікір жалған болғанда 0 мәнін қабылдайтын Буль алгебрасының айнымалылары болып келеді.  Мұндай айнымалыларды логикалық айнымалылар (немесе Буль айнымалылары) деп атайды. Демек, келтірілген мысалдағы екі пікірді былай да жазуға болады: Х = 1; У = 0.

      Пікірлер қарапайым және күрделі болуы мүмкін. Пікірдің мәні қандай да болсын басқа бір пікірлердің мәндеріне тәуелсіз болса, ол қарапайым пікір деп аталады. Ақиқаттық мәні басқа пікірлердің мәндері арқылы анықталатын пікір күрделі пікір болып саналады. Кез келген күрделі пікір кейбір екілік аргументтердің, яғни қарапайым пікірлердің логикалық функциясы болып табылады. Қарапайым логикалық пікірлерді қарастырайық.

      Олардың көмегімен қарапайым пікірлерден күрделі пікір құрастыруға болатын сияқты ЭЕМ-нің тораптары мен блоктары құрылады. Элементар пікір деп басқа пікірлерге жіктеуге келмейтін пікірді айтамыз. Егер пікірді басқа пікірлерге жіктеуге болатын болса, онда оны құрама пікір деп атайды. Мысалы, пікір: С: « 5 > 2» - элементар, ал пікір D: « 5 > 2» және « 5 – тақ сан» -құрама болады, өйткені ол екі пікірден: бірі «5 > 2» , ал екіншісі « 5 – тақ сан» деген пікірлерден құралады.

     Құрама пікірлер әр түрлі жалғаулықтар және сөз тіркестері арқылы элементар пікірлерден құралады. Мысалы: қарастырылған D пікірі «және» жалғаулығы арқылы элементар пікірлерден құралған. Ал мына «берілген төртбұрыш - ромб немесе квадрат» деген пікір «берілген төртбұрыш - ромб» деген және «берілген төртбұрыш - квадрат» деген екі пікірден «немесе» деген жалғаулық арқылы құралып тұр.

    Құрама пікірді «егер . . ., онда ...», «сонда және тек сонда» деген сөздерді пайдаланып та алуға болады.

     Мысалы: « Егер үшбұрыш тең қабырғалы болса, онда ол тең бүйірлі», «төртбұрыштың диагональдары қиылысу нүктесінде қақ бөлінетін болса, сонда және тек сонда ғана ол төртбұрыш параллелограмм болады».

     Грамматикада «және», «немесе», «егер ..., онда ...», «сонда және тек сонда» және осыларға ұқсас айтылуларды байлам, жалғаулық деп атайды. Логикада оларды сөйлемдер арасындағы байламдар деп атайды, өйткені мұндай жалғаулықтар екі пікірді бір құрама пікірге біріктіреді.

    Сөйлем арасында қолданылатын тағы бір « ... дұрыс емес» дейтін тіркесті қарастырайық. Ондай тіркес қандай да пікірді теріске (жоққа) шығару мақсатында қолданылады. «Біз жазда саяхатқа барамыз дегеніміз дұрыс емес» деген сөйлем «Біз жазда саяхатқа барамыз» деген сөйлемді теріске шығарады. Сөйлем арасында « ... дұрыс емес» тіркесін қоссақ, онда біз жаңа сөйлем аламыз. Сонымен « ... дұрыс емес» тіркесі қандай да бір екі сөйлемді бір сөйлемге байланыстырмағанымен оны логикада байлам деп санайды.

2.4 Әдісі

Логикалық әдіс — белгілі бір логикалық жүйеге келтірілген жаңа білімге жету тәсілдерінің жиынтығы. Философия мен басқа да ғылымдар тарихында әр түрлі Логикалық әдістер дамыған. Мысалы, Аристотельдің дедуктивтік-силлогистиктік әдісі, индуктивтік-логикалық әдіс, аксиоматиктік әдіс, гипотетиктік-дедуктивтік әдіс, диалектикалық-логикалық әдіс, т.б. ұыл. зерттеуде Логикалық әдіс туралы мәселе күрделі объектілерді теорияда талдау кезінде туындайды. Мұндай объектілерді теория жүзінде қайта жаңғырту үшін диалектикалық-логикалық әдіс қолданылады. Ол үшін оны неден бастау керектігін, яғни бастама мәселесін қарастыру қажет. Бастама ретінде зерттеліп отырған жүйенің ең қарапайым қатынасы, “торлы көзі” алынады. Мұны талдау кезінде оның қайшылықтары ашылып, оларды шешу жолдары сараланады.Диалектиканың категориялары мен принциптері осындай талдаудың жалпы қаңқасын анықтап береді. Диалектикалық-логикалық талдаудың бұл жолын абстрактіліктен нақтылыққа өту әдісі деп атайды.

Логикалыққа, ең алдымен, белгілі қасиеттеріне байланысты нақты тәртіппен орналастыру қажет нысандарды анықтауды талап ететін мәтіндік есептер жатады. Онымен қоса тапсырма шарттарының кейбірі әртүрлі ақиқаттық бағамен алға шығады. Логикалық есептер класына құю және өлшеу есептеріде жатады.

Логикалық есептерді шешудің әдістері жеткілікті. Оның әрқайсысының өзіндік қолдану аясы бар.

Келесі әдістерді қарастырамыз:

1.           Ойлау әдісі

2.           Ақиқат кестелер ідісі

3.           Гафтар әдісі

Ойлау әдісі

Бұл әдіспен ең қарапайым логикалық есептер шешіледі. Оның идеясы ойлау арқылы тапсырмалардың барлық шартын ретімен қолданып, тапсырма жауабы болатын қорытындыға келеміз.

Мысал қарастырайық.

Садық, Нұрғали және Абылай қытай, жапон, араб тілдерін үйреніп жатыр. Әрқайсысы қандай тілді меңгереді деген сұраққа біреуі былай жауап береді: «Садық қытай тілін үйреніп жатыр, Нұрғали қытай тілін үйреніп жатқан жоқ, Абылай араб тілін үйреніп жатқан жоқ». Соңында бұл жауаптың біреуі ғана дұрыс, қалған екеуі жалған болып шықты. Қайсысы қандай тіл үйреніп жатыр?

Шешуі:

Нұрғали қытай тілін, Абылай жапон тілін, Садық араб тілін оқып жатыр.

Ақиқат кестелер әдісі

Бұл мәтіндік логикалық есептерді шешу үшін қолданылатын негізгі әдіс. Кестелер есептің шартын немесе жауабын көрнекті түрде ұсынып қана қоймай, есепті шешу кезінде айтарлықтай дәрежеде дұрыс логикалық қорытынды жасауға көмектеседі. 

      Бұлардан күрделірек пікірлерді Буль функцияларының шарты негізгі жиынтығы арқылы құруды мына мысалмен көрсетуге болады: « Кітап қызықты болса және бос уақытым болса немесе өзіме қажетті сұраққа жауап іздесем және оны осы кітаптан табамын деп үміттенсем ғана кітап оқимын». Менің кітап оқу шартымды анықтайтын күрделі функция мынандай логикалық өрнекпен жазылады:

                              Ф( Х1, Х2, Х3, Х4) = ( Х1 & Х2) Ú (Х3 & Х4)              (3)

    Мұндағы, Х1 – «кітап қызық болса»;   Х2 – «бос уақытым болса»;  Х3 – «сұраққа жауап іздесем»;  Х4 – «жауап табам деп үміттенсем»

    Логикалық ЖӘНЕ, НЕМЕСЕ, ЕМЕС функцияларының арасындағы қызғылықты байланыстарды Морган теоремаларымен былайша сипаттайды:

                         Х1 & Х2 = Х1 & Х2;       (4)

                         Х1 Ú Х2 = Х1 & Х2;        (5)

     Эйлер – Венн диаграммаларын қарастырып та бұл формулаларды оңай алуға болады. Екі шеңбердің қиылысындағы(6-б,в суреттер) штрихталған аймақ Х1 &Х2 конъюнкциясына сәйкес келетіндіктен, жазықтықтың штрихталмаған бөлігі Х1&Х2 өрнегін анықтайды. Алайда штрихталмаған аймаққа Х1 және Х2 аймақтарының біреуі енетінін ескеріп, оны басқаша, яғни Х1 ÚХ2 өрнегімен де сипаттауға болады.

    Штрихталмаған аймақтың екі өрнегін теңестіріп, Х1&Х2 = Х1Ú Х2(6-формула) теңдігін аламыз.

   Буль алгебрасының ең маңызды теоремалары келесі таблицада келтірілген:

     1а  0 = 1                                                             1б  1 = 0

     2а  ХÚ 0 = Х                                                      2б  Х&1 = Х

     3а   ХÚ1 = 1                                                       3б  Х &0 = 0

     4а   Х Ú Х = X                                                   4б  Х&Х = X

     5а   Х ÚХ = 1                                                     5б  Х &Х = 0

     6а  (Х)Ú Х

     7а  Х1ÚХ2 = Х2ÚХ1                                         7б  Х1&Х2 = Х2&Х1

     8а  Х1ÚХ1&Х2 = Х1                                        8б  Х1&(Х1ÚХ2) = Х1

     9а  Х1ÚХ1&Х2 = Х1ÚХ2                                 9б  Х1&(Х1ÚХ2) = Х1&Х2

   10а  (Х1ÚХ2)ÚХ3 = Х1Ú (Х2ÚХ3)=                10б  Х1&(X2&X3) = (X1&X2)&X3 =

                                  = X1ÚX2ÚX3                                                       = X1&X2&X3

    11a  X1ÚX2&X3 = (X1ÚX2)&(X1ÚX3)          11б  X1&(X2ÚX3) = X1&X2ÚX1&X3

     Келтірілген байланыстар Буль өрнектерін түрлендіру ережелерін береді. Олардың көмегімен эквивалент өрнектер алуға болады. Жаңа өрнектер қарапайым болып шығуы мүмкін. Ол, атап айтқанда, жабдықтардың үнемделуіне және ЭЕМ-нің функционалдық (қызметтік) тораптарының әрекет тездігін көтеруге жеткізеді.

     Логикалық элементтердегі информацияны өңдейтін күрделі схемалар, логикалық ЖӘНЕ (И), НЕМЕСЕ (ИЛИ) және ЕМЕС(НЕ) элементтерінен жинастырылады. Логикалық элементтер белгілі тәртіппен жалғанған диод, транзистор, резистор мен конденсаторлардан тұрады. Техникада арнаулы интегралды технологиямен жасалған жартылай ткізгішті логикалық элементтер кеңінен қолданылады.

      Логика алгебрасында 0 және 1 сандары айтылатын ой-пікірлердің, тұжырымдардың шындығын және жалғандығын сипаттау үшін қолданылады. Информациялық хабарды жеткізуді қамтамасыз ететін физикалық шаманың өзгерісін сигнал деп атайды. Қабылдағышты ток немесе кернеу өзгерісі ретінде көрсететін электр сигналы ЭЕМ-де информация тасымалдаушы болып табылады. Информация көзінің міндеті осы өзгерісті туғызу. Егер электр сигналы уақыт бойынша үзіліссіз болса, оны аналогты сигнал деп атайды(7 – сурет)

          U

 

                                     уақыт                                              t

                                     7 - сурет

 

     Бұл сигнал информацияны кернеу немесе токтың үзіліссіз өзгерісі түрінде тасымалдайды. Керісінше, үзілісті болыпкелетін сигнал дискретті немесе цифрлы сигнал деп аталады.

     Цифрлы сигналдар екі дискретті аймақта мән қабылдайды, сондықтан олар екі түрлі күй : « қосылған- ажыратылған», « ақиқат – жалған», « 0 – 1» анық сипатталған процестер туралы информацияны жеткізуге жақсы бейімделген. Жартылай өткізгіштік технологияның бастапқы жемісі – жартылай өткізгішті диодтар болды. Олардың негізгі қасиеті – электр тогын тек бір ғана бағытта өткізуі – кейбір логикалық функцияларды жүзеге асыру үшін пайдаланылды. Одан кейін диодтардың ауыстырып қосқыш қасиетін информацияның еске сақтау құрылғыларын дайындау мүмкіндігімен толықтырған приборлар – транзисторлар шықты. Транзисторлар мен диодтардың көмегімен жартылай өткізгіштік технология ЭЕМ-нен радиолампыларды ығыстырып, машиналардың әрекет тездігін едәуір арттырды, онымен қатар аппаратураның көлемі мен салмағын азайтты.

     60-жылдары интегралдық схемалар (ИС) жасалды. Олар резисторлар, конденсаторлар, диодтар, транзисторлар, элемент аралық байланыстар, электр көзінің тізбегі құрамына кіретін әдеттегі радиоэлектрондық схемалардың алуан түрлі құрылымдарын ықшам түрде қайта жасап шыығарады. Интегралдық схема – белгілі бір функцияларды орындауға арналған толық электрондық құрылғы.

      Логикалық функцияларды іске асыруға арналған интегралдық схемаларды ЕМЕС теріске шығару логикалық функциясын іске асыратын инвентордан бастаймыз: инвентордың жұмысы осы функцияның ақи қаттық таблицасымен толық сипатталады.  9 – а суретте  инвентор схема түрінде көрсетілген.

 

                                                                                   

                                                кіріс                    шығыс   

                                                           9 – а сурет

     Оның мұндай шартты кескінделуі есептеу машиналарының схемаларында пайдаланылады.  9-б суретте  инвентордың уақыттық диаграммасы – инвентор арқылы өткен сигналдың уақытқа тәуелділігінің графигі берілген.

                      U_кір

 

                                           Y

 

                                                                                
                                           t                       

                        U_шығ             

 

                                                                 уақыт                                                t          

                                                     

                                                            9 – б сурет

    Инвентордың кірісіне кернеу мөлшері логикалық функция аргументінің мәніне сәйкес цифрлы сигнал беріледі. Мысалы: Х = 1 үшін бұл кернеу +5 В, ал Х = 0 үшін 0 В болады.

                                              Лог. 1

                                                              +5 в

                            Лог. 0

                                                                            

                                                                                
      0 в

                                        9 – в сурет

      Қарапайым ИС-ның стандартты корпусына (19х7,2х3,2мм) алты инвентор орналастырылады. Бұдан басқа логикалық көбейту функциясын іске асыруға арналған конъюнктор және логикалық қосу функциясын іске асыратын дизъюнктор ИС базалық элементтері болып табылады.10-а суретте конъюнктордың схемалы көрсетілуі,10-б суретте оның уақыттық диаграммасымен көрсетілген.

                                                                         X₁

                                                                                
                       &           Y

Шығыс

                                                                          X₂

		кірістер

 

                                                                                
              10 – а сурет

        U_кір     

 

                                Х₁  

 

                                                                                
                                          t

          U_кір      

                           Х₂

 

                                                                                                                 
        t

 

        U_шығ   

 

                              y

 

                                                                                
                                           t

                                                  10 - б  сурет

Контакт тұйықталғанда Х = 1, контакт ажыратылғанда Х = 0, егер тізбекте ток болса У = 1, ал тізбекте ток болмаса У = 0.

     ЖӘНЕ функциясын іске асыратын интегралдық схеманы  үйлесу схемасы деп атайды.

     НЕМЕСЕ функциясын іске асыратын ИС-ны құрастыру схемасы деп атайды: егер кірістердің ең болмағанда біріне логикалық бірлік сигналы келсе, онда шығыста логикалық бірлік деңгейге сәйкес келетін сигнал пайда болады.

    11 а,б - суреттерде сәйкесінше дизъюнктордың схемалық белгіленуі, оның уақыттық диаграммасы келтірілген.

 

                                                 Х₁

                                                                                           У

                                                  Х₂          

 

                                                              11 – а сурет

 

       U_шығ          

 

                                                                         

                                                                                
                                     t

 

            U_кір

 

                                                                                
                                     t                                                                               
                                      

 

            U_шығ

 

                                                                                
                                     t                                                                               
                                       

                                                    11 – б сурет

    Инвентор мен үйлесу схемасын біріктіру нәтижесінде ЖӘНЕ – ЕМЕС функциясын іске асыратын схема алуға болады ( 12-а сурет),

                X₁                                                                                            
                                    X₁     

                                          Y                 Y                       Y                                                                      Y

                              &                    +                   1                     =                    &                    1  

                X₂                                                                                      X₂

 

                                                                 12 – а сурет

 « ЖӘНЕ – ЕМЕС» ИС-нің белгіленуі 12-б суретте келтірілген.

                                                    Х₁

                                                                           &         У

                                                    Х₂

 

 ЖӘНЕ – ЕМЕС  схемасы ҮИС-ны (Үлкен Интегралдық Схемалар)  жасап шығаратын «тетіктердің» бірі.  Бұл схеманың әмбебаптығы (жан-жақтылығы) одан инвенторды оңай алуға (13-а сурет),

 

                             X        &          Y                     X          1            Y

                                                                 =      

                                                                   

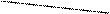
және де

                            Х1 & Х2 = Х1 Ú Х2                          (4)

    Морган теоремасын пайдаланып, НЕМЕСЕ функциясын өрнектеуге болатындығында ( 13-б сурет).

 

          X₁            &

 

                                                    &                         X₁        1      

                                                                     =                                   Y          

                                                                                X₂

 

        X₂

 

                        &

      Сонымен , қорытындылай келгенде осындай логикалық шағын элементтер негізінде қазіргі замандағы есептеу техникасының интегралды микросхемалары дайындалады. Бұл мақалада Буль алгебрасы мен электрондық логикалық элементтердің арасындағы терең де принципті байланыс ашып көрсетілді. «ЖӘНЕ», «ЕМЕС», «НЕМЕСЕ» логикалық схемаларының көмегімен ЭЕМ-нің негізгі ИС-ларын қарастыруға болады.

ЖӘНЕ жалғаулығының көмегімен қарапайым екі А мен В айтылымдарының бір құрамдасқа бірігуі логикалық көбейту немесе конъюнкция (латынша соіушісііо -біріктіру), ал операцияның нәтижесі - логикалық көбейтінді деп аталады.

ЖӘНЕ операциясы «.» нүктемен белгіленеді (& белгісімен де белгіленуі мүмкін).

Біріктіруші мағынада қолданылатын НЕМЕСЕ жалғаулығының көмегімен қарапайым А және В айтылымдарының бір құрамдасқа бірігуі логикалық қосу немесе дизъюнкция(латышда disjuncnctio - бөлу), ал операцияның нәтижесі – логикалық қосынды деп аталады. НЕМЕСЕ логикалық операциясы белгісімен (кейде + белгісімен белгіленеді).

Қарапайым А айтылымына ЕМЕС шылауын қосу логикалық терістеу операциясы деп аталады, операцияны орындау нәтижесінде ЕМЕС операциясы айтылымның үстіне сызықша салумен белгіленеді. Құрылымдық схемалардағы конъюнкция операциясы «&» белгісімен белгіленеді («амперсэнд» деп оқылады), бұл and деген ағылшын сөзінің қысқартылып жазылуы.

ҚОРЫТЫНДЫ

       Логикалық зандар барлық адамзаттын, ойлау мәдениетінің нәтижесінде қалыптасты. Терт формалды-логикалық заңның авторлары (Аристотель мен Лейбниц) оларды тек дәстүрлі формалды логикада бөлінетін негізгі заң ретівде анақтады және негіздеді.  Жеткілікті негіздеу заңы кез келген ақиқатты қорытындының басқа ақиқатты қорытындылармен жеткілікті түрде негізделуін талап етеді.Үшіншінің жоққа шыгарылу заңы былай дейді: бір-біріне қарама-қайшы түжырымдамалардың біреуі — ақиқат, екіншісі — жалған. Үшінші жол жоқ. Бүл заңның формуласы мынандай: a v -i a. Қарама-қайшыльщ емес заңы келесідей айтуға болатын заң: бір зат туралы екі түрлі карама-қайшы түжырымдамада бір мезгілде, бір мәнде бірдей акиқат болуы мүмкін емес. Символ түрінде бүл заңның формуласын былайша беруге болады: -і(ал->а). Үқсастық заңы бойынша кез келген түжырымдама немесе пайымдау процесінде өзіне-езі үқсас болып қалуы керек. Басқаша айтқанда, талдау барысывда кейбір түсініктердің немесе терминдердің мәндерін ерікті түрде өзгертуге болмайды. Жаңа заман логикасында үқсастық заңы былайша беріледі: кез келген тұжырымдама өзін-өзі білдіреді. Әр түжырымдама өзінің ақиқаттығының қажетгілігі және жеткілікті шарты болып табылады. Үқсастық заңының формуласы былай: а=а, (А=А) немесе а->а.

.

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ

1.     О. Камардинов «Жасанды интеллект. Сараптаушы жүйелер. Пролог». Шымкент, 2003.

2.     И. Братко «Программирование на языке Пролог для искусственного интеллекта». Москва, 1990.

3.     Клоксин, Меллиш «Програмирование на языке Пролог». Москва, 1987.

4.     Дж. Стобо «Язык программирования Пролог». Москва, 1993.

5.     Ин Ц., Соломон Д. «Использование Турбо-Пролога». Москва, 1993.

6.     Хоггер «Введение в логическое программирование». Москва, 1988.

7.     Фёдоров А. «Особенности программирования на Borland Pascal». Киев, 1994.

8.     Л. Стерлинг, Э. Шапиро «Искусство программирования на языке Пролог». Москва, 1990г.

9.     Кларк К., Маккей Ф. «Введение в логическое программирование на микро-Прологе».  Москва, 1987.

10.                  И. Братко «Алгоритмы искусственного интеллекта на языке Пролог».    Москва, 2004.

11.                   Доорс Дж., Рейблейн А.Р., Вадера С. «Пролог — язык программирования будущего». Москва, 1990.