МИНИСТЕРСТВО ОБРАЗОВАНИЯ и науки РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Интеллектуальный анализ данных – Data Mining Forecasting: прогностическое моделирование, методы прогнозирования, Time-Series Data Mining.
ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ, НЕЧЕТКАЯ ЛОГИКА.
Выполнил студент 4 курса
ФКТиПМ КубГУ
Степанов Роман
Краснодар 2013
СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 3
1 Подготовка данных для анализа. 5
2 Процесс анализа данных. 8
3 Деревья прогнозирования. 10
4 Метод ближайшего соседа. 14
5 Time-Series Data Mining. 18
6 Генетические алгоритмы.. 22
7 Нечеткая логика. 27
ЗАКЛЮЧЕНИЕ. 32
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ.. 33
ВВЕДЕНИЕ
Современные крупные компании, как правило, используют сложные интегрированные информационные системы, которые проникают во все аспекты бизнеса и порождают постоянно растущий объем данных. Этот процесс многие специалисты называют Big Data. Однако для получения конкурентных преимуществ компаниям стало необходимо не только извлекать и хранить информацию, но анализировать ее, выявлять скрытые закономерности, прогнозировать. Возникла необходимость в объединении информации из разрозненных источников, применении хорошо известных методов анализа и разработке новых, а также в использовании специальных структур данных для представления информации в компьютере.
В 1992 году в журнале «Artificial Intelligence» (Искусственный интеллект) Уильям Фроули дал следующее определение Data Mining:
Data Mining – нетривиальное извлечение скрытой, заранее неизвестной и потенциально полезной информации из массива данных. Термин Data Mining обозначает не столько конкретную технологию, сколько сам процесс поиска, тенденций, взаимосвязей и закономерностей с помощью различных математических и статистических алгоритмов. Также он тесно связан с чисто техническими аспектами: организацией данных, обеспечением требуемого уровня быстродействия и т.д.
Популяризация данного направления породила несколько соседствующих технологий: OLAP, СХД, инструменты Business Intelligence. На данный момент в совокупности данные технологии очень востребованы, как и специалисты данных направлений востребованы на рынке труда.
Идея построения компьютерных систем, адаптивных к внешней среде и накапливающих «жизненный опыт» привлекла ученых из различных областей: инженерия, математика, физика, когнитивная психология.
Приведенными выше высказываниями объясняется актуальность выбранной темы.
Целью работы является изучение основных концепций Data Mining. Для достижения поставленной цели предполагается решение следующих задач:
1. Раскрыть понятие хранилищ данных
2. Обозначить этапы анализа данных
3. Описать методы Data Mining
В отечественной литературе тема использования методов Data Mining в информационных системах остается слабо проработанной. Связано это с тем, что область является еще относительно молодой, и, к сожалению, технологии в ней создают не российские, а американские компании (Oracle, IBM, HP). В западных странах предмет Data Mining и смежные являются частью университетской программы.
1 Подготовка данных для анализа
Как правило, информационная система компании в очень упрощенном виде представляет собой несколько взаимодействующих реляционных баз данных и приложений, реализующих интерфейс пользователя. В таких базах данных хранится оперативная информация, и их называют Online Transaction Processing (OLTP). Как правило, для анализа данных такая структура хранения не годится по причине низкого быстродействия при выполнении сложных «аналитических» запросов. Это происходит по двум причинам:
1. Базы данных находятся на разных физических носителях, и соединение таблиц из разных баз получается очень дорогостоящим (по времени) процессом.
2. Для анализа часто требуются агрегированные показатели (за месяц, год, и т.д.). Как уже было сказано, в обычные реляционные базы записывают оперативную информацию. Например, в базу данных записываются операции продажи, а для анализа продаж нам нужны суммарные данные за полгода. На выполнение такого запроса уйдет много времени.
Поэтому для хранения данных для анализа проектировщики строят хранилища данных (Data Warehouses).
Согласно Уильяму Иммону (одному из основателей концепции Data Warehousing), хранилище данных – интегрированная предметно-ориентированная неизменная во времени коллекция данных, с помощью которой осуществляется поддержка принятия решений.
Данные в большинстве OLTP-систем архивируются сразу после того, как они становятся неактивными. Например, заказ может стать неактивным после того, как он выполнен; банковский счет может стать неактивным после того, как он был закрыт. Главная причина для архивирования неактивных данных — это производительность OLTP-системы (зачем хранить данные, если к ним не обращаются). Большие объемы таких данных могут заметно ухудшить производительность выполнения запросов в предположении, что обрабатываются только активные данные. Для обработки таких данных в СУБД предлагаются различные процедуры разбиения базовых таблиц на секции. С другой стороны, поскольку хранилища предназначены, в частности, быть архивом для OLTP-данных, данные в них хранятся в течение очень длительного периода.
Перечислим некоторые различия между традиционными базами данных и хранилищами:
1. Избыточность данных.
Реляционная теория гласит о необходимости нормализации данных с целью устранения избыточности и аномалий. Хранилища же допускают дублирование данных, поскольку хранят данные из самых разных источников. Также они чаще всего денормализованы, т.к. содержат заранее вычисленные агрегаты.
2. Структура.
Одним из популярных способов представления моделей классических баз данных является модель «Сущность-связь» (Entity-Relationship, ER). Для хранилища характерна схема «звезда» (Star Schema).
Общая схема хранилищ данных изображена на рисунке 1.
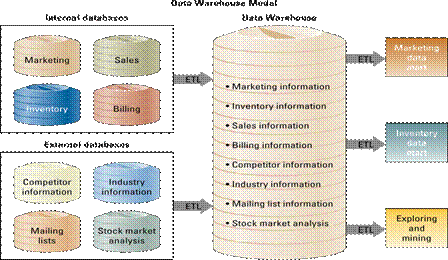
Рисунок 1 – Схема хранилищ данных
Данные из оперативных источников попадают в хранилище, откуда потом распределяются по витринам данных (data mart). Витрина данных представляет собой часть хранилища, отвечающую за определенную область деятельности компании (например, маркетинг).
Замечание: стрелками изображен процесс ETL (Extract, Transform, Load) – «извлечение, преобразование, загрузка».
2 Процесс анализа данных
После построения хранилища данных следует перейти непосредственно к анализу информации. Но прежде необходимо озвучить классы задач, которые позволяют решить алгоритмы, объединенные под общим понятием Data Mining:
1. Исследование данных: в этом случае мы изучаем данные без какой-либо определенной цели. Результатом этого процесса может быть графическое представление исследуемого объекта с помощью графиков, кубов данных. С ростом числа показателей составление графического представления начинает вызывать трудности.
2. Описание данных: примером может служить составление математической модели, разделение данных на группы (кластерный анализ и сегментирование). Сегментирование может с успехом использоваться для разделения клиентов на потребительские группы, кластерный анализ еще в 1971 году использовался для определения таксономии психиатрических заболеваний.
3. Прогностическое моделирование: цель состоит в построении модели, которая позволит предсказать будущие значения для исследуемой переменной. Прогностическое моделирование включает широкий набор методов статистики и машинного обучения. Прекрасным примером успешного применения является разработка системы SKICAT в 1996 году. Она использовала метод деревьев классификации и регрессии. Удалось провести обучение с целью классификации звезд и созвездий, которые подавались на вход в виде вектора признаков, состоящего из 40 компонент.
4. Извлечение шаблонов и правил: примером служит выявление высокой вероятности появления различных событий (можно использовать даже в спортивной статистике), или обнаружение мошенничеств.
5. Поиск по шаблону: цель по существующему шаблону найти похожие. Такие задачи решаются при поиске релевантных документов, сравнении лиц на фотографиях.
Исходя из решаемых задач, описанных выше, можно сделать вывод, что основу Data Mining составляют методы классификации, моделирования и прогнозирования, основанные на применении деревьев решений, искусственных нейронных сетей, генетических алгоритмов, эволюционного программирования, ассоциативной памяти, нечёткой логики. К методам Data Mining иногда относят статистические методы (корреляционный и регрессионный анализ, факторный анализ, дисперсионный анализ, анализ временных рядов). Такие методы, однако, предполагают некоторые априорные представления об анализируемых данных, что несколько расходится с целями Data Mining (обнаружение ранее неизвестных нетривиальных знаний).
Процесс анализа включает в себя 3 стадии:
1. Постановка целей анализа
2. Выявление закономерностей
3. Прогностическое моделирование – использует результаты второй стадии.
4. Анализ исключений
Прогностическая модель – научно обоснованное суждение о возможных состояниях объекта в будущем. Прогностическую модель получают на этапе прогностического моделирования путем обучения прогностического метода на данных, которые мы исследуем.
Рассмотрим методы, которые могут использоваться для выявления закономерностей и дальнейшего прогнозирования состояния исследуемого объекта.
3 Деревья прогнозирования
Деревья прогнозирования (также известны как «деревья решений», деревья принятия решений», decision trees) – семейство алгоритмов, основанных на создании иерархической структуры, которая базируется на ответе "Да" или "Нет" на набор вопросов. Такие алгоритмы позволяют предсказать значение какого-либо параметра для заданного случая.
Основные виды задач, решаемые с помощью деревьев прогнозирования:
- Описание данных: деревья решений позволяют хранить информацию о данных в компактной форме.
- Классификация: деревья решений отлично справляются с задачами классификации, т.е. отнесения объектов к одному из заранее известных классов. Целевая переменная должна иметь дискретные значения.
- Регрессия: Если целевая переменная имеет непрерывные значения, деревья решений позволяют установить зависимость целевой переменной от независимых (входных) переменных. Например, к этому классу относятся задачи численного прогнозирования (предсказания значений целевой переменной).
Простой алгоритм построения дерева решений.
1. Выбрать признак, по которому будет строиться дерево.
Для того, чтобы выбрать признак разбиения, пользуются индексом Джини (Gini):
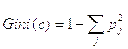
Здесь c – текущий узел дерева, p(j) - вероятность класса j в узле дерева. Также для выбора признака можно использовать эвристический подход (т.е. перебрать все признаки).
2. Разбить объекты согласно выбранному признаку на классы и распределить их по узлам нового яруса дерева.
3. При необходимости выбрать другой признак разбиения и повторить действие 2.
4. При выполнении критерия остановки вернуть ответ. Обычно в качестве критерия остановки используют 2 метода:
- Установить заранее максимальную глубину дерева
- Разбиение должно быть нетривиальным (получившиеся в результате разбиения подмножества должны содержать не менее заданного количества элементов)
Описанная процедура лежит в основе многих современных алгоритмов построения деревьев решений, этот метод известен еще под названием «Разделяй и властвуй». Очевидно, что при использовании данной методики, построение дерева решений будет происходить сверху вниз.
Замечание: метод «Разделяй и властвуй» предполагает разбиение задачи на элементарные подзадачи, их решение и объединение полученных решений.
Поскольку все объекты были заранее отнесены к известным нам классам, такой процесс построения дерева решений называется обучением с учителем (supervised learning). Процесс обучения также называют индукцией деревьев (tree induction). Действие алгоритмов построения деревьев решений базируется на применении методов регрессионного и корреляционного анализа. Один из самых популярных алгоритмов этого семейства - CART (Classification and Regression Trees), основанный на разделении данных в ветви дерева на две дочерние ветви.
Преимущества деревьев решений:
1. Извлечение правил на естественном языке;
2. Интуитивно понятная классификационная модель;
3. Высокая точность прогноза
Недостатки:
1. Применяемый для обучения деревьев решений алгоритм рекурсивного секционирования по своему характеру является жадным. Этот алгоритм показывает относительно высокую производительность, но обычно не позволяет достичь оптимальных результатов.
Замечание: жадный алгоритм на каждом шаге делает локально наилучший выбор в надежде, что итоговое решение будет оптимальным. Преимуществами же такого алгоритма являются простота его реализации и время исполнения.
2. Очень часто алгоритмы построения деревьев решений дают сложные деревья, которые имеют много узлов и ветвей. Такие деревья очень трудно воспринимать. К тому же дерево, имеющее много узлов, разбивает обучающее множество на все большее количество подмножеств, состоящих из все меньшего количества объектов.
Ценность правила, справедливого для 2-3 объектов, крайне низка, и в целях анализа данных такое правило практически непригодно. Гораздо предпочтительнее иметь дерево, состоящее из малого количества узлов, которым бы соответствовало большое количество объектов из обучающей выборки. И тут возникает вопрос: а не построить ли все возможные варианты деревьев, соответствующие обучающему множеству, и из них выбрать дерево с наименьшей глубиной? Эта задача является NP-полной, что было показано Л. Хайфилем и Р. Ривестом.
Замечание: задачи, относящиеся к классу NP-полных, не имеют эффективных алгоритмов решения.
Для решения вышеописанной проблемы часто применяется так называемое отсечение ветвей.
Пусть под точностью (распознавания) дерева решений понимается отношение правильно классифицированных объектов при обучении к общему количеству объектов из обучающего множества, а под ошибкой – количество неправильно классифицированных. Предположим, что нам известен способ оценки ошибки дерева, ветвей и листьев. Тогда, возможно использовать следующее простое правило:
- построить дерево
- отсечь или заменить поддеревом те ветви, которые не приведут к возрастанию ошибки
В отличие от процесса построения, отсечение ветвей происходит снизу вверх, двигаясь с листьев дерева, отмечая узлы как листья, либо заменяя их поддеревом. Хотя отсечение не является панацеей, но в большинстве практических задач дает хорошие результаты.
Обычно алгоритмы этого семейства применяются для решения задач, позволяющих разделить все исходные данные на несколько дискретных групп.
Пример построения дерева решений в программе STATISTICA приведен в приложении А.
4 Метод ближайшего соседа
Известен также как метод k ближайших соседей (k-Nearest Neighbour, далее – KNN).
В простейшем случае этот метод требует:
1. Целое число k
2. Множество объектов (training set), на которых будет проводиться обучение
3. Метрика, с помощью которой можно определить, что объекты «похожи»
Объекты, которые находятся близко друг другу, склонны иметь близкие значения предсказываемых величин — это главная идея метода ближайших соседей. Если вы знаете предсказываемое значение для одного из элементов, вы можете предсказать его и для ближайших соседей.
Аксиома соседства:
Пусть (X, d) будет метрическим пространством и пусть S∈X будет конечным множеством, элементы которого классифицируются через функцию f:S→{1,2,..m}. Мы говорим, что S удовлетворяет аксиоме соседства, если для каждой точки x∈S есть y ближайшая к x, тогда f(x)=f(y). То есть y разделяет тот же класс, что и x, если y ближайший сосед x.
Функция 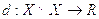 называется метрикой, если она удовлетворяет следующим условиям:
называется метрикой, если она удовлетворяет следующим условиям:
Пусть 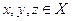 . Тогда:
. Тогда:
1. Неотрицательность: 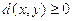 и
и 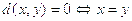
2. Симметричность: 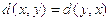
3. Удовлетворяет неравенству треугольника: 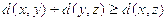
Некоторые распространенные метрики:
1. Евклидово расстояние:
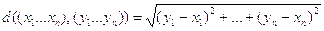
2. Метрика Чебышева:
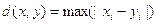
Подставив произвольные значения в формулы данных метрик, можно убедиться, что все 3 условия выполняются.
На рисунке 2 имеется 3 класса, требуется классифицировать элемент x. В качестве метрики используется Евклидово расстояние, число k выбрано равным пяти. Из 5 ближайших соседей элемента x 4 принадлежат множеству  , 1 элемент принадлежит множеству
, 1 элемент принадлежит множеству  , множеству
, множеству  не принадлежит ни одного элемента. Поэтому мы относим элемент x к множеству
не принадлежит ни одного элемента. Поэтому мы относим элемент x к множеству  .
.
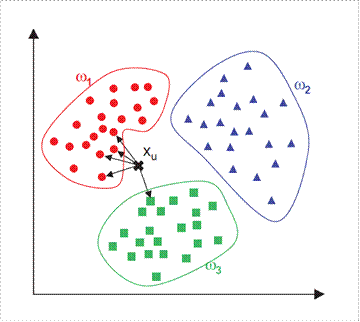
Рисунок 2
Алгоритм k-ближайших соседей имеет широкое применение:
1. Обнаружение мошенничества. Новые случаи мошенничества могут быть похожи на те, которые происходили когда-то в прошлом. Алгоритм KNN может распознать их для дальнейшего рассмотрения.
2. Предсказание отклика клиентов. Можно определить отклик новых клиентов по данным из прошлого.
3. Медицина. Алгоритм может классифицировать пациентов по разным показателям, основываясь на данных прошедших периодов.
4. Прочие задачи, требующие классификации.
В заключение следует отметить достоинства и недостатки алгоритма KNN.
Достоинства:
1. Алгоритм устойчив к аномальным выбросам, так как вероятность попадания такой записи в число k-ближайших соседей мала. Если же это произошло, то влияние на голосование (при k>2), скорее всего, будет незначительным, и, следовательно, малым будет и влияние на итог классификации. Пример изображен на рисунке 3: увеличение числа k позволяет избежать аномальных выбросов.
2. Программная реализация алгоритма относительно проста.
3. Результат работы алгоритма легко поддаётся интерпретации. Экспертам в различных областях вполне понятна логика работы алгоритма, основанная на нахождении схожих объектов.
4. Возможность модификации алгоритма, путём использования наиболее подходящих функций сочетания и метрик позволяет подстроить алгоритм под конкретную задачу.
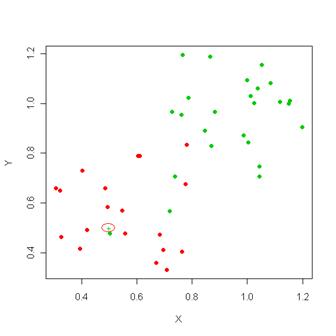
Рисунок 3 – При увеличении k удалось правильно классифицировать новый элемент (он оказался красным)
Недостатки:
1. Набор данных, используемый для алгоритма, должен быть репрезентативным.
2. Модель нельзя "отделить" от данных: для классификации нового примера нужно использовать все примеры. Эта особенность сильно ограничивает использование алгоритма, поскольку возникает необходимость полного перебора обучающей выборки при распознавании, следствие этого – вычислительная трудоемкость.
3. Существует сложность выбора меры "близости" (метрики). От этой меры главным образом зависит объем множества записей, которые нужно хранить в памяти для достижения удовлетворительной классификации или прогноза. Также существует высокая зависимость результатов классификации от выбранной метрики.
С помощью данного метода решаются задачи классификации и регрессии.
5 Time-Series Data Mining
Time-Series переводится как «временной ряд». Временной ряд – последовательно измеренные через некоторые (зачастую равные) промежутки времени данные.
Основные цели анализа временных рядов:
1. определить природу ряда
2. предсказать будущие значения ряда
Большинство регулярных составляющих временных рядов принадлежит к двум классам: они являются либо трендом, либо сезонной составляющей. Тренд представляет собой общую систематическую линейную или нелинейную компоненту, которая может изменяться во времени. Сезонная составляющая - это периодически повторяющаяся компонента. Оба эти вида регулярных компонент часто присутствуют в ряде одновременно.
Можно выделить 3 основных модели временных рядов:
1. Авторегрессионные модели
2. Интегральные модели
3. Модели скользящего среднего
Авторегрессионная модель описывается уравнением:
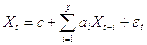
где 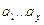 — параметры модели (коэффициенты авторегрессии), c -постоянная (часто для упрощения предполагается равной нулю), а
— параметры модели (коэффициенты авторегрессии), c -постоянная (часто для упрощения предполагается равной нулю), а 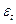 — белый шум.
— белый шум.
Для p=1, с=0 принимает вид:
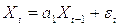
Time-Series Database («БД временного ряда») – база данных, хранящая данные временного ряда. В отличие от обычной базы, порядок записей в БД временного ряда имеет значение.
Имеется 2 подхода к хранению временных рядов в РБД:
1. Хранить как большие двоичные объекты (BLOB), и соответственно для них иметь только 2 операции – вставить BLOB в базу и извлечь BLOB из базы.
2. Хранить информацию о времени в дополнительном поле базы. И значению времени в этом поле будут соответствовать значения других параметров. Однако такой подход является неэффективным.
В качестве примера рассмотрим ведение торгов ценными бумагами. Спроектируем простую базу данных для этих целей:
| Дата сделки | Время сделки | Код бумаги | Цена |
| ... | ... | ... | ... |
| 03.07.2012 | 13:45:00 | 1236 | 12.0000 |
| 03.07.2012 | 13:45:02 | 1240 | 34.0300 |
| 03.07.2000 | 13:45:03 | 1236 | 12.0100 |
| 03.07.2000 | 13:45:07 | 1450 | 56.1300 |
| ... | ... | ... | ... |
Для анализа временного ряда используются данные, относящиеся только к одной ценной бумаге. Из таблицы будут извлекаться записи, относящиеся к одной ценной бумаге по порядку возрастания или убывания отметок времени. Длина строки невелика - несколько десятков байт, поэтому в одной странице данных СУБД может помещаться порядка сотни записей. В большинстве приложений количество временных рядов для одного объекта составляет порядка ста. Т.е. для каждого временного ряда записи распределены примерно по одной на каждую страницу дискового пространства. Чтобы выбрать записи, относящиеся к одному временному ряду, необходимо обратиться практически к каждой странице данных. Часто на практике размер таблицы превосходит размер буферов СУБД. В такой ситуации практически каждое обращение к элементу временного ряда потребует чтения с диска. Из курса баз данных известна, что операция чтения с диска является самой дорогостоящей по времени.
Для хранения данных произвольной структуры в последнее время используются так называемые NoSQL СУБД.
Одной из важных проблем в настоящее время является извлечение схожих временных последовательностей из базы данных (similarity retrieval of time sequences). Классический алгоритм «грубой силы» дает ожидаемое время исполнения O(nm), где n – количество записей в базе, m – длина последовательности. Очевидно, что такой запрос будет выполняться неприемлемо долгое время.
Формально данная задача звучит следующим образом:
Пусть d – расстояние между последовательностями, 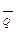 – заданная последовательность.
– заданная последовательность.
Найти множество последовательностей R, удовлетворяющих условию:
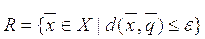 ,
,
где 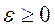
Если |R|=k, то задача сводится к поиску k ближайших соседей временной последовательности.
Одним из популярных методов решения данной задачи является кусочно-постоянная аппроксимация (Piecewise Constant Approximation), предложенная Кьоу (Keogh) и Паццани (Pazzani) в 2000 году. Идея заключается в том, что непрерывный сигнал можно аппроксимировать с помощью постоянной, равной среднему значению на этом интервале:

Поэтому следует разбить последовательность на k равных частей и взять среднее значение каждой такой части в качестве координаты для вектора размерности k. Результат аппроксимации указан на рисунке 4. После такой трансформации вычислять схожие последовательности можно аналогично методу KNN.
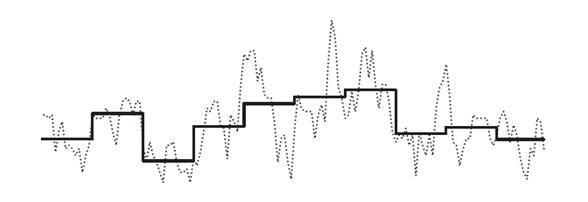
Рисунок 4 - Piecewise Constant Approximation
6 Генетические алгоритмы
Предложенные сравнительно недавно — в 1975 году в Мичиганском университете — Джоном Холландом генетические алгоритмы (далее – ГА) основаны на принципах естественного отбора Ч. Дарвина.
Теория эволюции Дарвина утверждает, что развитие любой биологической особи заключается в целенаправленном изменении себя таким образом, чтобы лучше приспособиться к условиям окружающей среды. Приобретение животными защитной окраски, развитие у человека сложной и разветвленной нервной системы и многое другое – все это результат работы многолетнего процесса эволюции. Говоря языком математики, эволюция природы – это процесс оптимизации живых организмов.
Главная трудность с возможностью построения вычислительных систем, основанных на принципах естественного отбора и применением этих систем в прикладных задачах, состоит в том, что природные системы достаточно хаотичны, а все наши действия, фактически, носят четкую направленность. Мы используем компьютер как инструмент для решения определенных задач, которые мы сами и формулируем, и мы акцентируем внимание на максимально быстром выполнении при минимальных затратах. Природные системы не имеют никаких таких целей или ограничений, во всяком случае нам они не очевидны. Выживание в природе не направлено к некоторой фиксированной цели, вместо этого эволюция совершает шаг вперед в любом доступном ее направлении.
Возможно это большое обобщение, но я полагаю, что усилия, направленные на моделирование эволюции по аналогии с природными системами, к настоящему времени можно разбить на две большие категории:
1) системы, которые смоделированы на биологических принципах. Они успешно использовались для задач типа функциональной оптимизации и могут легко быть описаны на небиологическом языке
2) системы, которые являются биологически более реалистичными, но которые не оказались особенно полезными в прикладном смысле. Они больше похожи на биологические системы и менее направлены. Они обладают сложным и интересным поведением, и, видимо, вскоре получат практическое применение.
ГА работают с популяцией, где каждая особь представляет возможное решение данной проблемы. Каждая особь оценивается мерой ее приспособленности согласно тому, насколько «хорошо» соответствующее ей решение задачи. Наиболее приспособленные особи получают возможность воспроизводить потомство с помощью перекрестного скрещивания с другими особями популяции. Это приводит к появлению новых особей, которые сочетают в себе некоторые характеристики, наследуемые ими от родителей. Наименее приспособленные особи с меньшей вероятностью смогут воспроизвести потомков, так что те свойства, которыми они обладали, будут постепенно исчезать из популяции в процессе эволюции.
Рассмотрим классический генетический алгоритм.
1. Инициализация. Каждая особь популяции является кандидатом на решение задачи. Формирование исходной популяции, как правило, происходит с использованием случайного закона. Особи популяции могут состоять как из одной, так и из нескольких хромосом. Каждая хромосома особи в свою очередь состоит из генов, причем количество генов в хромосоме определяется количеством параметров решаемой задачи (аргументов целевой функции).
Кодирование генов происходить с помощью кодов Грея. Основной недостаток двоичного кодирования заключается в том, что соседние числа отличаются в значениях нескольких битов, так например числа 7 и 8 в битовом представлении различаются в 4-х позициях, что затрудняет функционирование генетического алгоритма и увеличивает время, необходимое для его сходимости. Кодирование по коду Грея решает эту проблему.
2. Оценивание приспособленности хромосом в популяции состоит в расчете функции приспособленности для каждой хромосомы этой популяции. Чем больше значение этой функции, тем выше «качество» хромосомы. Предполагается, что функция приспособленности всегда принимает неотрицательные значения и для решения оптимизационной задачи требуется максимизировать эту функцию.
3. Селекция хромосом. Оператор селекции (reproduction, selection) осуществляет отбор хромосом в соответствии со значениями их функции приспособленности. Одним из популярных методов селекции является метод рулетки. Он отбирает особей с помощью n "запусков" рулетки. Колесо рулетки содержит по одному сектору для каждого члена популяции. Размер i-ого сектора пропорционален соответствующей величине Psel(i) вычисляемой по формуле:
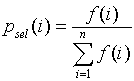
При таком отборе члены популяции с более высокой приспособленностью с большей вероятностью будут чаще выбираться, чем особи с низкой приспособленностью.
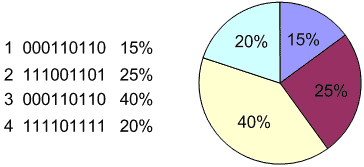
Рисунок 5 - Оператор селекции типа колеса рулетки
При таком отборе члены популяции с более высокой приспособленностью с большей вероятностью будут чаще выбираться, чем особи с низкой приспособленностью.
4. На первом этапе скрещивания выбираются пары хромосом из родительской популяции, отобранной в результате селекции. Определяется (обычно случайным образом) точка скрещивания. Потомки определяются как конкатенации частей первого и второго родителя. Затем с вероятностью 0,5 определяется одна из результирующих хромосом в качестве потомка.
Оператор мутации предназначен для того, чтобы поддерживать разнообразие особей с популяции. При использовании данного оператора каждый бит в хромосоме с определенной вероятностью инвертируется.
5. Формирование новой популяции. Хромосомы, полученные в результате применения генетических операторов к хромосомам временной родительской популяции, включаются в состав новой популяции. Она становится текущей популяцией для данной итерации генетического алгоритма. На каждой очередной итерации рассчитываются значения функции приспособленности для всех хромосом этой популяции, после чего проверяется условие остановки алгоритма и либо фиксируется результат в виде хромосомы с наибольшим значением функции приспособленности, либо осуществляется переход к следующему шагу генетического алгоритма, т.е. к селекции.
Преимущества ГА:
1. Простота реализации
2. Подходят для решения крупномасштабных проблем оптимизации
3. Могут быть использованы для решения широкого класса задач
4. Не требуют никакой информации о поведении целевой функции (например, дифференцируемости и непрерывности)
Недостатки:
1. Трудно найти точный глобальный оптимум (напоминают жадные алгоритмы)
2. Неэффективно применять в случае оптимизации функции, требующей большого времени на вычисление
3. ГА трудно применить для изолированных функций. Изолированность
(«поиск иголки в стоге сена») — проблема для любого метода оптимизации, поскольку функция не предоставляет никакой информации, подсказывающей, в какой области искать максимум. Пример изолированной функции изображен на рисунке 6.
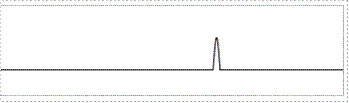
Рисунок 6 – Изолированная функция
7 Нечеткая логика
Основы теории нечетких множеств.
Пусть U — так называемое универсальное множество, из элементов которого образованы все остальные множества, рассматриваемые в данном классе задач (например, множество всех целых чисел, множество всех гладких функций и т.д.). Характеристическая функция множества 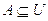 – это функция
– это функция 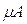 , значения которой указывают, является ли
, значения которой указывают, является ли 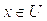 элементом множества A:
элементом множества A:
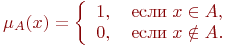
В теории нечетких множеств характеристическая функция называется функцией принадлежности, а ее значение 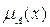 — степенью принадлежности элемента x нечеткому множеству A. Эта функция принимает любые значения на отрезке от 0 до 1. Например, высказывание «x зерен не образует кучи» истинно только в некоторой степени
— степенью принадлежности элемента x нечеткому множеству A. Эта функция принимает любые значения на отрезке от 0 до 1. Например, высказывание «x зерен не образует кучи» истинно только в некоторой степени 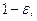 где
где 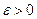 .
.
Нечетким множеством A называется совокупность пар
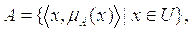
где 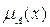 — функция принадлежности, т.е.
— функция принадлежности, т.е. 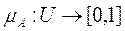 .
.
Пример. Пусть U - множество действительных чисел. Нечеткое множество A, обозначающее множество чисел, близких к 10, можно задать функцией принадлежности, изображенной на рисунке 7:
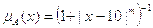 ,
,
где 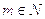
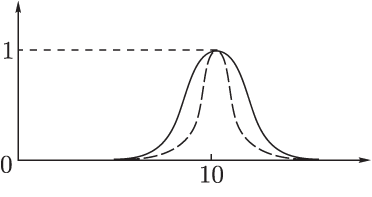
Рисунок 7 - Функция принадлежности нечеткого множества A
Степень принадлежности – это не вероятность, т.к. неизвестна функция распределения, нет повторяемости экспериментов. Значения функции принадлежности могут быть взяты только из априорных знаний, интуиции, опыта, опроса экспертов.
Для нечетких множеств, как и для обычных, определены основные логические операции. В теории нечетких множеств разработан общий подход к выполнению операторов пересечения, объединения и дополнения. Приведенные ниже на рисунках 8-10 реализации операций – наиболее распространенные.
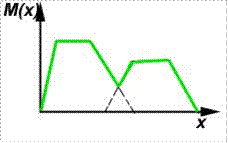
Рисунок 8 – Объединение
Рисунок 9 – Пересечение
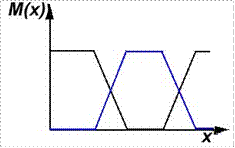
Рисунок 10 – Дополнение
Любая нечеткая переменная характеризуется тройкой 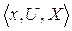 , где x — название переменной, U — универсальное множество, X — нечеткое подмножество множества U.
, где x — название переменной, U — универсальное множество, X — нечеткое подмножество множества U.
Значениями лингвистической переменной являются не числа, а слова естественного языка, называемые термами. Рассмотрим такое нечеткое понятие как "Цена акции". Это и есть название лингвистической переменной. Сформируем для нее базовое терм-множество, которое будет состоять из трех нечетких переменных: "Низкая", "Умеренная", "Высокая" и зададим область рассуждений в виде X=[100;200] (единиц). Теперь необходимо построить функции принадлежности для каждого лингвистического терма.
Существует свыше десятка типовых форм кривых для задания функций принадлежности. Наибольшее распространение получили: треугольная, трапецеидальная и гауссова функции принадлежности. Они изображены на рисунках рядом с соответствующими формулами.
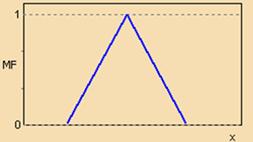
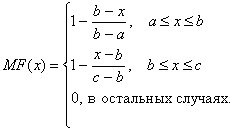
Рисунок 11 – Треугольная функция принадлежности
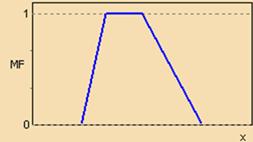
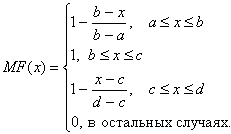
Рисунок 12 – Трапецеидальная функция принадлежности
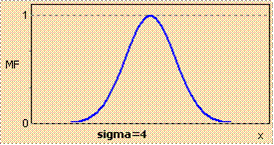
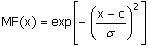
Рисунок 13 – Гауссова функция принадлежности
Таким образом, для терм-множества лингвистической переменной "Цена акции" функции принадлежности имеют вид, указанный на рисунке.
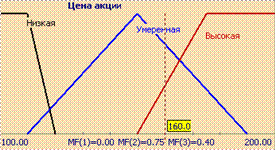
Рисунок 14 – Функции принадлежности для терм-множества лингвистической переменной "Цена акции"
Модель нечеткого вывода.
Схематично модель нечеткого вывода имеет вид, представленный на рисунке 15:
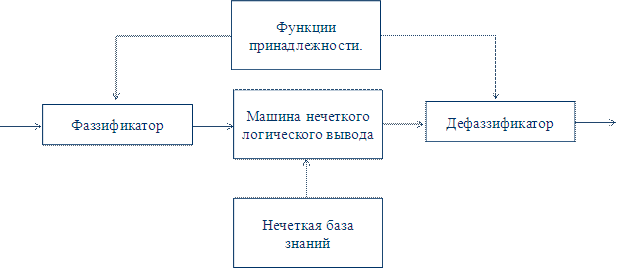
Рисунок 15 – Модель нечеткого вывода
Одним из наиболее распространенных способов логического вывода в нечетких системах является механизма Мамдани. Рассмотрим его подробнее.
1. Процедура фазификации: определяются степени истинности, т.е. значения функций принадлежности для левых частей каждого правила (предпосылок). Для базы правил с m правилами обозначим степени истинности как Aik(xk), i=1..m, k=1..n.
2. Нечеткий вывод. Сначала определяются уровни "отсечения" для левой части каждого из правил:
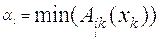
3. Далее находятся "усеченные" функции принадлежности:
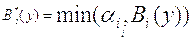
4. Композиция, или объединение полученных усеченных функций, для чего используется максимальная композиция нечетких множеств:

где MF(y) – функция принадлежности итогового нечеткого множества.
5. Дефазификация, или приведение к четкости. Существует несколько методов дефазификации. Например, метод среднего центра:
 .
.
Рассмотрим следующую постановку задачи:
Пусть Y – результирующая характеристика, 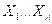 – входные факторы. С помощью датчика проведены измерения n параметров m объектов. Каждый объект измеряли k раз. Таким образом, имеем обучающую выборку данных, представленную матрицей M , которая имеет n+1 столбцов и m*k строк:
– входные факторы. С помощью датчика проведены измерения n параметров m объектов. Каждый объект измеряли k раз. Таким образом, имеем обучающую выборку данных, представленную матрицей M , которая имеет n+1 столбцов и m*k строк:
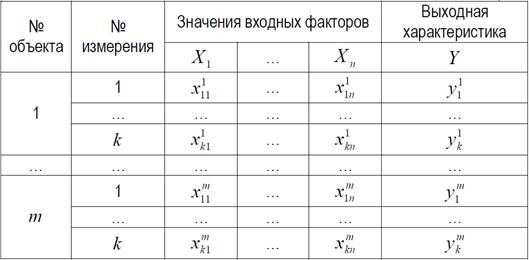
Необходимо по результатам измерений восстановить значения Y для всех новых объектов.
Рассмотрим, каким образом может быть решена данная задача при помощи аппарата нечеткой логики:
Пусть 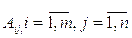 – лингвистическая переменная (далее – ЛП), которая строится на множестве значений фактора
– лингвистическая переменная (далее – ЛП), которая строится на множестве значений фактора 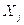 объекта i , то есть на множестве значений
объекта i , то есть на множестве значений 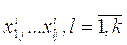 , которое является универсальным множеством данной ЛП.
, которое является универсальным множеством данной ЛП.
Пусть 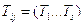 - терм-множество ЛП
- терм-множество ЛП 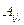 , каждому элементу которого соответствуют функции принадлежности (далее – ФП)
, каждому элементу которого соответствуют функции принадлежности (далее – ФП) 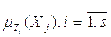 .
.
В качестве функций принадлежности для элементов терм-множества будем использовать следующие:
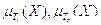 – линейные
– линейные
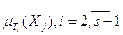 – имеют треугольный вид.
– имеют треугольный вид.
ФП изображены на рисунке 16:
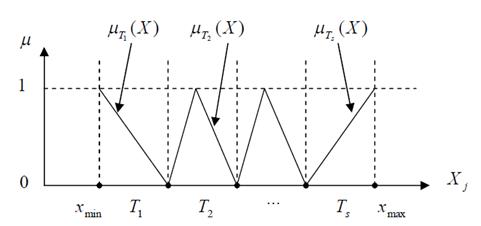
Рисунок 16 – ФП для элементов терм-множества
Формируем нечеткую базу знаний. Пусть модель прогнозирования выходной характеристики задается набором правил 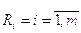 :
:
Если 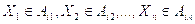 , то
, то 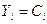 ,
,
где 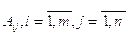 - ЛП,
- ЛП, 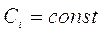
В соответствии с механизмом нечеткого вывода Сугэно получаем следующий алгоритм прогнозирования выхода Y при заданном входном объекте 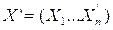 :
:
1. Рассчитать степени выполнения посылки i -го правила для входного вектора X’:
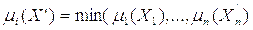 ,
, 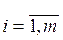
2. В результате выполнения шага 1 получаем нечеткое множество, которое соответствует входному вектору X’:
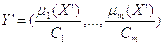
3. Выполнить дефазификацию  можно одним из следующих способов:
можно одним из следующих способов:
3.1. Найти взвешенное среднее:
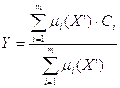
3.2. Найти взвешенную сумму:
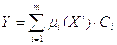
В состав среды MatLab входит пакет прикладных программ Fuzzy Logic Toolbox. Он позволяет создавать системы нечеткого логического вывода и нечеткой классификации в рамках среды MatLab, с возможностью их интегрирования в Simulink.
Областью внедрения алгоритмов нечеткой логики являются всевозможные экспертные системы, в том числе:
- нелинейный контроль над процессами (производство);
- самообучающиеся системы (или классификаторы), исследование рисковых и критических ситуаций;
- распознавание образов;
- финансовый анализ (рынки ценных бумаг);
Достоинства:
1. Нечеткая логика предлагает совершенно иной уровень мышления, благодаря которому творческий процесс моделирования происходит на высоком уровне абстракции, при котором постулируется лишь минимальный набор закономерностей.
2. Позволяет моделировать поведение сложных систем
Недостатки:
1. Отсутствие стандартной методики конструирования нечетких систем, интерпретация полученного результата субъективна.
2. Применение нечеткого подхода по сравнению с вероятностным не приводит к повышению точности вычислений.
ЗАКЛЮЧЕНИЕ
Data Mining – прикладная область, но, как мы убедились, обладающая обширной теоретической базой. Для успешной реализации методов на практике требуются знания в области математической статистики, теории нейронных сетей, алгоритмов и структур данных, теории множеств и т.д. Важно понимать сильные и слабые места различных алгоритмов, уметь адаптировать их под конкретную задачу.
В результате выполнения работы были изучения ключевые концепции Data Mining. По возможности были затронуты смежные темы. В дальнейшем для успешного продолжения изучения данной области следует, прежде всего, обратить внимание на технические аспекты, плохо освещенные в отечественной литературе. Ведь методы анализа далеко не новы, а способы их реализации с помощью современных компьютерных технологий постоянно совершенствуются.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. http://www.aiportal.ru/ - портал искусственного интеллекта
4. http://www.codenet.ru – Портал для программистов
2. http://algolist.manual.ru/ – Библиотека алгоритмов и структур данных
3. http://www.basegroup.ru/ – Официальный сайт компании «Basegroup»
5. http://www.neuroproject.ru/ – Официальный сайт компании «Нейропроект»
6. http://www.pwc.ru/ - PWC Россия
7. Чубукова И.А. Data Mining – материалы с сайта http://www.intuit.ru
7. Штовба С.Д. Введение в теорию нечетких множеств и нечеткую логику – материалы с сайта http://matlab.exponenta.ru
9. Giudici P. Applied Data Mining – John Wiley & Sons Ltd, 2003
10. Hand D., Mannila H., Smyth P. Principles of Data Mining - The MIT Press, 2001
11. Last M., Kandel A., Bunke H. Data Mining in Time Series Databases – World Scientific Publishing Co, 2004
Приложение А
Пример построения дерева решений в программе STATISTICA.
Требуется оценить, какие клиенты банка потенциально являются более надежными (кредитоспособными). Имеются следующие данные по существующим клиентам:
| Клиент | Возраст | Семейное положение | Надежность |
| 1 | 36 | 1 | 1 |
| 2 | 32 | 0 | 0 |
| 3 | 38 | 1 | 1 |
| 4 | 40 | 0 | 0 |
| 5 | 44 | 1 | 1 |
| 6 | 56 | 1 | 1 |
| 7 | 58 | 0 | 0 |
| 8 | 30 | 0 | 1 |
| 9 | 28 | 1 | 0 |
| 10 | 26 | 1 | 0 |
Семейное положение:
1 – женат/замужем
0 – не женат/не замужем
Надежность:
1 – надежный
2 – ненадежный
Импортируем данные в STATISTICA:
Выбираем пункт Data Mining – General Classification/Regression Tree Models. В открывшемся окне задаем параметры построения:
В окне Variables задаем зависимую переменную (надежность) и атрибуты (возраст и семейное положение):
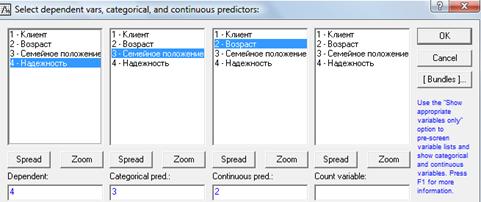
Нажимаем ОК, и в появившемся окне на вкладке Summary нажимаем Tree Graph. Получившееся дерево появится на экране (изображено на рисунке ниже). Сначала разбиение идет по атрибуту «Возраст», затем по атрибуту «Семейное положение». Доля надежных и ненадежных клиентов изображена с помощью гистограмм.
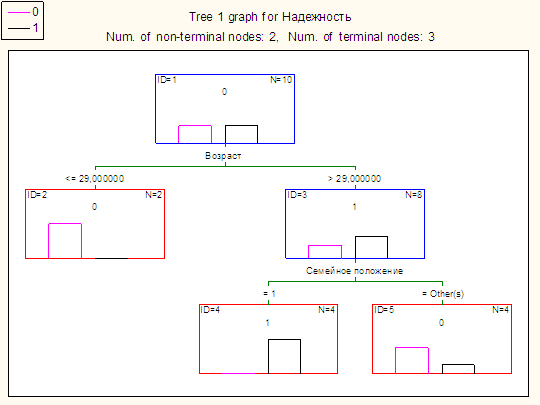
Приложение Б
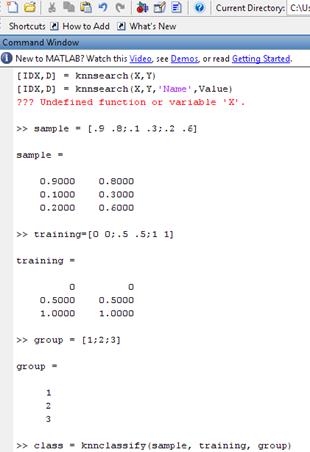
Пример использования алгоритма k-ближайших соседей в среде MATLAB.
Sample – матрица, чьи строки должны классифицироваться на группы. Group пронумеровывает эти группы. Функция knnclassify() распределяет строки матрицы Sample по группам, основываясь на распределении по группам строк матрицы Training. Пример указан на следующем рисунке:
Следующий пример классифицирует строки матрицы Sample на 2 группы и возвращает график:
sample = unifrnd(-5, 5, 100, 2);
% Classify the sample using the nearest neighbor classification
c = knnclassify(sample, training, group);
gscatter(sample(:,1),sample(:,2),c,"mc"); hold on;
legend("Training group 1","Training group 2", ...
"Data in group 1","Data in group 2");
hold off;
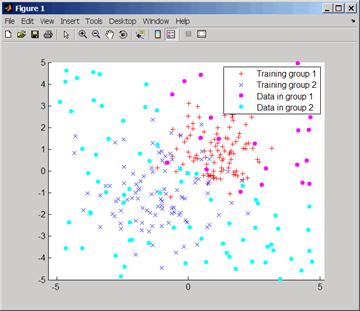
График решения задачи соседства
Приложение В
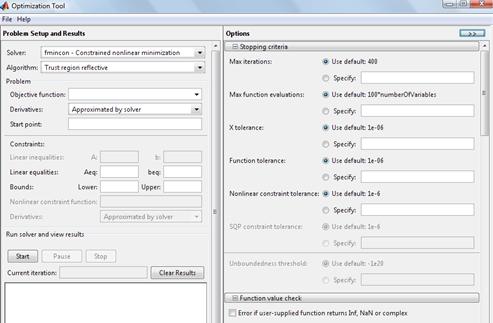
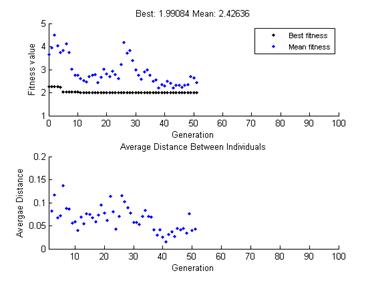
Пример использования генетического алгоритма в среде MATLAB.
В терминале MATLAB необходимо запустить команду optimtool("ga"). После этого в появившемся окне выбрать нужные параметры генетического алгоритма (тип алгоритма, вид функции принадлежности, ограничения инициализации начальной популяции и т.д.):
После прохождения итераций с применением генетических операторов график популяций меняет вид:














 (zip - application/zip)
(zip - application/zip)










