Федеральное агентство по образованию Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
Южно-Уральский государственный университет
Факультет «Энергетический»
Кафедра «Электропривод и автоматизация промышленных установок»
Синтез контура регулирования тока якоря двигателя постоянного тока
независимого возбуждения
Пояснительная записка к курсовой работе
по дисциплине «Теория нелинейных и импульсных систем регулирования»
Проверил, (преподаватель)
_________ /Н.А. Горожанкин /
«__» _______ 2016г.
Автор работы
студент группы Э-376
_________ /Е. . Максимов/
«__» _______ 2016г.
Курсовая работа защищена
с оценкой
_________
«__» ______ 2016г.
Аннотация
Е._. Максимов. Синтез контура регулирования тока якоря двигателя постоянного тока независимого возбуждения. – Челябинск: ЮУрГУ, Э-376, 27 с., 22 ил., 6 табл, библиогр. список – 3 наим., 1 прил.
Цель курсовой работы – выбор параметров регуляторов в контуре регулирования тока ДПТНВ, а также изучить влияние противо ЭДС двигателя на переходные процессы.
Для П и И регуляторов определены граничные значения коэффициента усиления и постоянной времени. Для ПИ регулятора определены из условий устойчивости область допустимых значений K и T. Также определены значения параметров различных видов регуляторов и сравнения их эффективности по полученным переходным процессам в программе MATLAB.
С помощью блока ограничения осуществлен разгон двигателя с заданным ускорением. Построены статические характеристики контура регулирования тока с пропорциональным и пропорционально-интегральным регуляторами.
Оглавление
Введение. 4
1 Исходные данные. 5
2 Расчёт параметров цепи якоря.. 7
3 Линеаризация статической характеристики преобразователя.. 8
4 Расчёт граничных параметров регуляторов тока.. 9
4.1 Передаточная функция схемы контура регулирования тока якоря (для П регулятора тока): 9
4.2 Передаточная функция схемы контура регулирования тока якоря (для И регулятора тока): 10
4.3 Передаточная функция схемы контура регулирования тока якоря (для ПИ регулятора тока): 11
5 Определение параметров регуляторов, обеспечивающих заданный показатель качества (по варианту – перерегулирование 5…10% при отработке задающего воздействия) 13
5.1 Параметры П регулятора. 13
5.1.1 С учётом противо ЭДС двигателя. 14
5.2 Параметры И регулятора. 15
5.2.1 С учётом противо ЭДС двигателя. 17
5.3 Параметры ПИ регулятора. 18
5.3.1 С учётом противо ЭДС двигателя. 20
6 Разгон двигателя с заданным ускорением.. 24
7 Статические характеристики контура регулирования тока с П и ПИ регуляторами.. 26
Библиографический список.. 27
Введение
Контур регулирования тока как самостоятельная подчинённая система регулирования очень часто используется в электроприводе и в источника вторичного электропитания. Основная его задача – ограничение тока на допустимом уровне для защиты силовых элементов от перегрузки по току и полное использование их по току в переходных режимах для повышения быстродействия системы.
В данной курсовой работе мы подберём параметры регуляторов тока и оценим показатели качества переходных процессов с разными контурами регулирования.
1 Исходные данные
Таблица 1
Исходные данные
|
№ варианта |
Тип двигателя |
|
|
|
|
|
|
|
|
|
|
Желаемый показатель качества переходного процесса |
|
7 |
Д32 |
9,5 |
0,425 |
220 |
0,28 |
57 |
800 |
2 |
0,5 |
0,02 |
0,006 |
Перерегулирование 5…10% при отработке задающего воздействия |
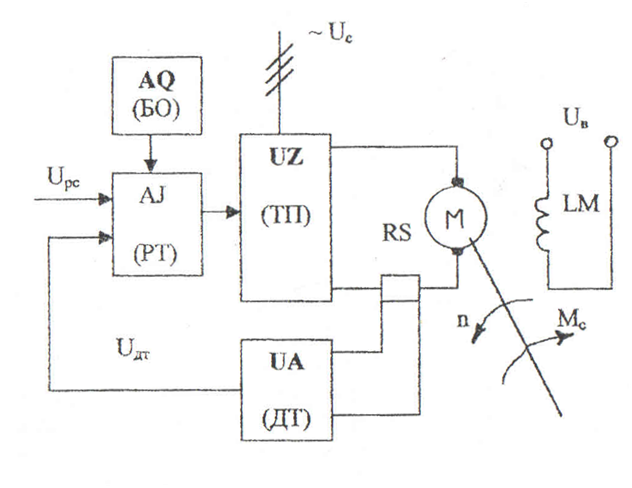
Рисунок 1. Функциональная схема контура регулирования тока якоря
Где UZ – тиристорный преобразователь, AQ – блок ограничения, AJ – регулятор тока, UA – датчик тока, RS – шунт, LM – обмотка возбуждения.
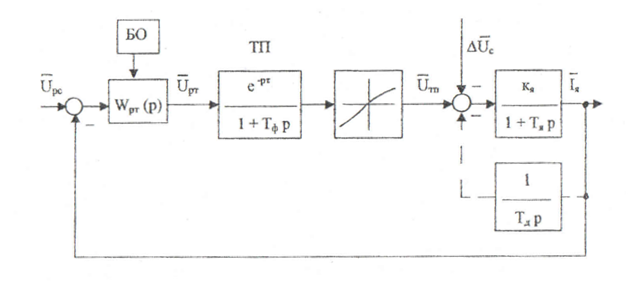
Рисунок 2. Структурная схема контура регулирования тока якоря
2 Расчёт параметров цепи якоря
Суммарная индуктивность якорной цепи:
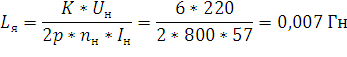
Электромагнитная постоянная времени якорной цепи:
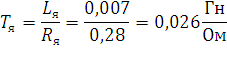
Кратность тока короткого замыкания:
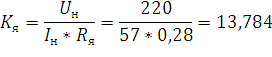
Номинальный момент двигателя:
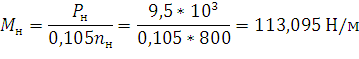
Скорость холостого хода двигателя:
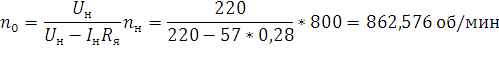
Механическая постоянная времени:
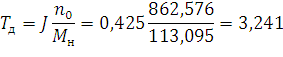
Так как 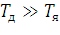 отбрасываем
обратную связь якорной цепи.
отбрасываем
обратную связь якорной цепи.
3 Линеаризация статической характеристики преобразователя
Таблица 2
Статическая характеристика преобразователя
|
|
0 |
0,05 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
1,1 |
1,2 |
|
|
0 |
0,02 |
0,035 |
0,085 |
0,17 |
0,28 |
0,42 |
0,55 |
0,69 |
0,8 |
0,89 |
0,94 |
0,98 |
1 |
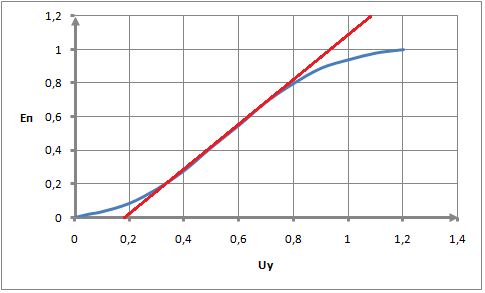
Рисунок 3. Линеаризация статической характеристики преобразователя
Линеаризуем, т.е. приведём к виду 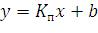
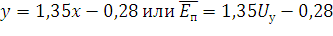
Также заменяем 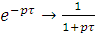 , так как
выполняется
, так как
выполняется 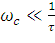 , где
, где 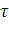 –
постоянная времени запаздывания.
–
постоянная времени запаздывания.
4 Расчёт граничных параметров регуляторов тока
Произведя подстановку рассчитанных звеньев получим следующую структурную схему контура регулирования тока якоря

4.1 Передаточная функция схемы контура регулирования тока якоря (для П регулятора тока):
Для П регулятора делаем замену 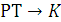
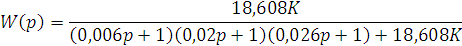
Для П регулятора определим граничное значение коэффициента усиления K, для этого воспользуемся критерием устойчивости Гурвица:
Характеристический полином замкнутой системы:
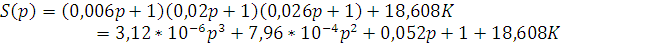
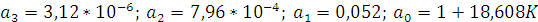
Так как система имеет третий порядок, то она будет находиться на границе устойчивости при следующем условии:
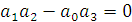
Откуда 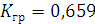
Проверяем:

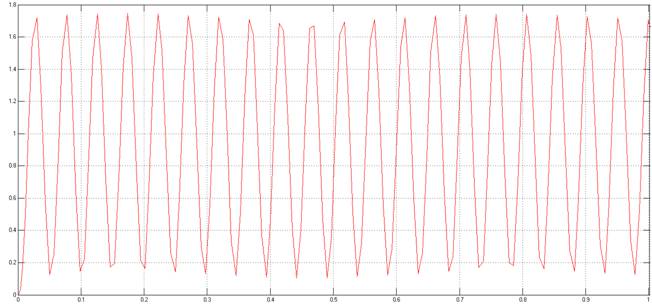
Рисунок 4. Переходный процесс с граничным K
4.2 Передаточная функция схемы контура регулирования тока якоря (для И регулятора тока):
Для И регулятора делаем замену 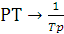
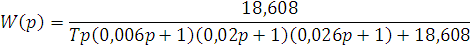
Для И регулятора определим граничное значение постоянной времени T, для этого воспользуемся критерием устойчивости Гурвица:
Характеристический полином замкнутой системы:
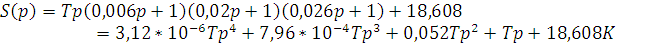
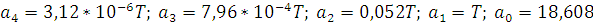
Так как система имеет четвертый порядок, то она будет находиться на границе устойчивости при следующем условии:
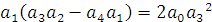
Откуда 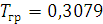
Проверяем:

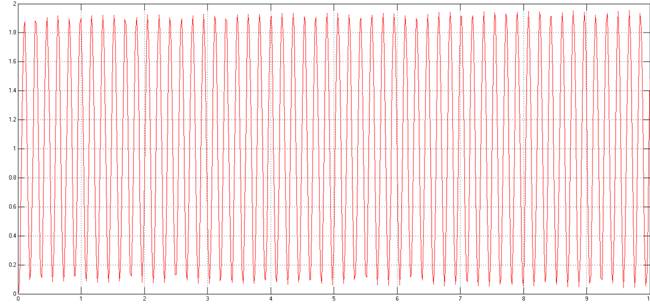
Рисунок 5. Переходный процесс с граничным T
4.3 Передаточная функция схемы контура регулирования тока якоря (для ПИ регулятора тока):
Для ПИ регулятора делаем замену 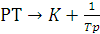
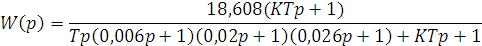
Характеристический полином замкнутой САУ:
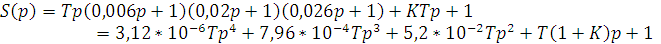
Для ПИ регулятора определим граничное значение постоянной времени T и коэффициента усиления K , для этого воспользуемся критерием устойчивости Гурвица:
границы области устойчивости будут при следующих уравнениях:
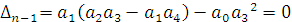
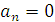
Коэффициенты получившегося характеристического полинома:
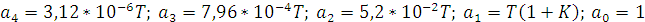
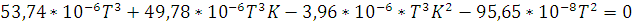
Откуда:
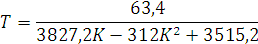
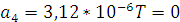
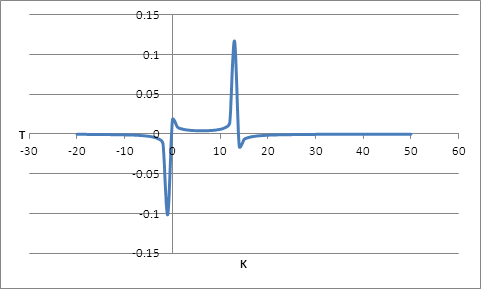
Рисунок 6. Область допустимых значений K и Т
5 Определение параметров регуляторов, обеспечивающих заданный показатель качества (по варианту – перерегулирование 5…10% при отработке задающего воздействия)
5.1 Параметры П регулятора

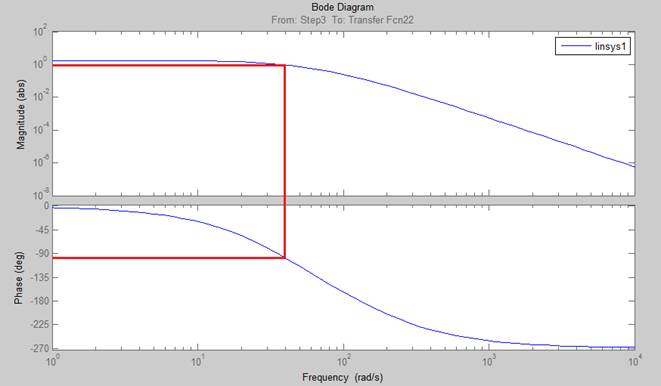
Рисунок 7. ЛАЧХ и ФЧХ с П регулятором
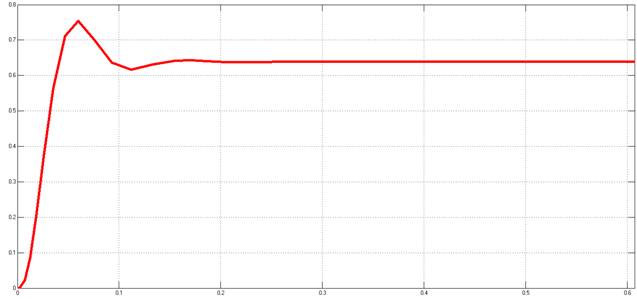 Рисунок 8.
Переходный процесс относительно задающего воздействия
Рисунок 8.
Переходный процесс относительно задающего воздействия
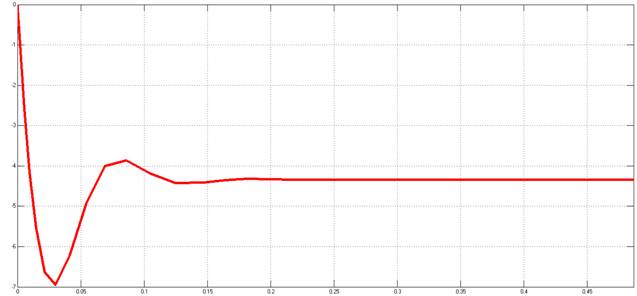
Рисунок 9. Переходный процесс относительно возмущающего воздействия
5.1.1 С учётом противо ЭДС двигателя
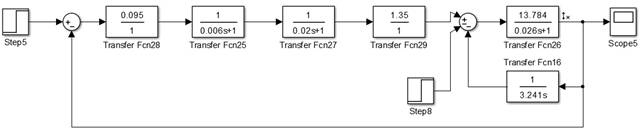
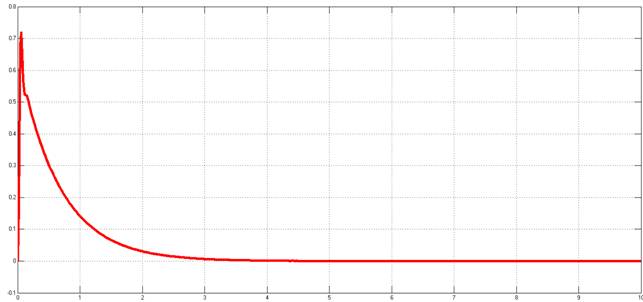
Рисунок 10. Переходный процесс относительно задающего воздействия с учётом противо-ЭДС двигателя
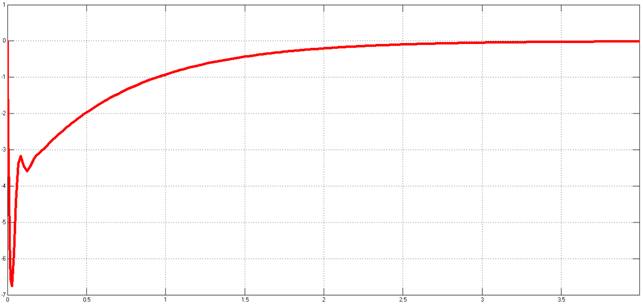
Рисунок 11. Переходный процесс относительно возмущающего воздействия с учётом противо ЭДС двигателя
5.2 Параметры И регулятора

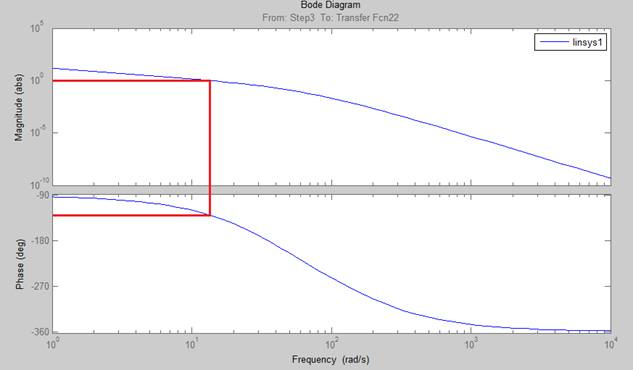
Рисунок 12. ЛАЧХ и ФЧХ И регулятора
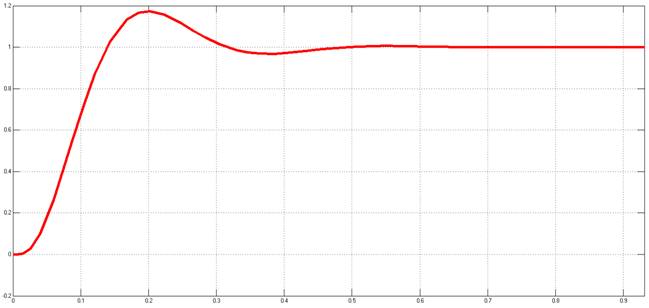
Рисунок 13. Переходный процесс относительно задающего воздействия
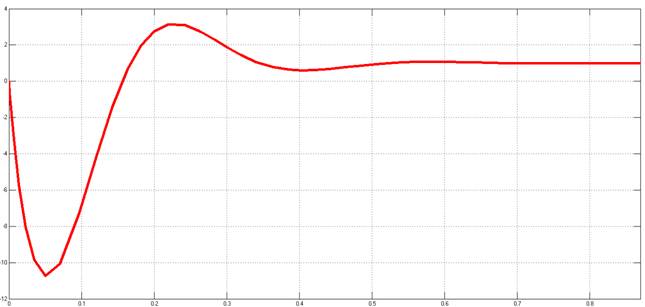
Рисунок 14. Переходный процесс относительно возмущающего воздействия
5.2.1 С учётом противо ЭДС двигателя
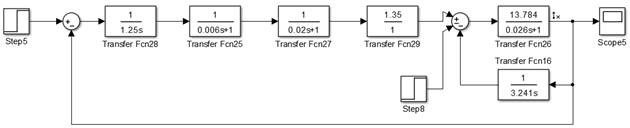
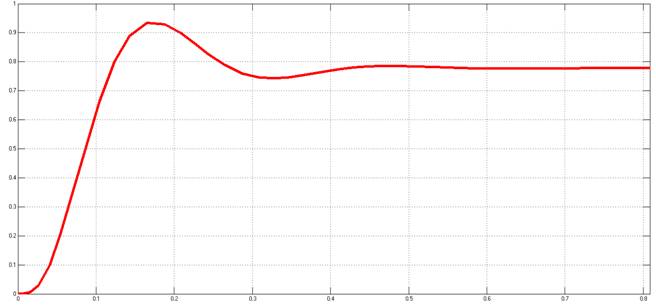
Рисунок 15. Переходный процесс относительно задающего воздействия с учётом противо ЭДС двигателя
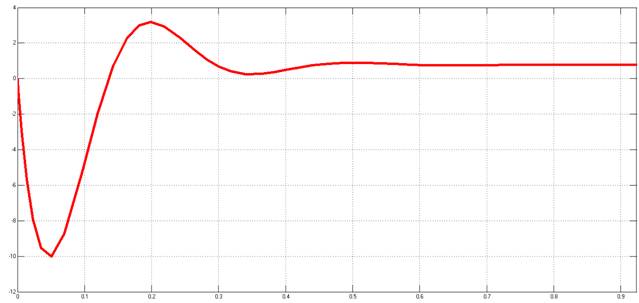
Рисунок 16. Переходный процесс относительно возмущающего воздействия с учётом противоЭДС двигателя
5.3 Параметры ПИ регулятора

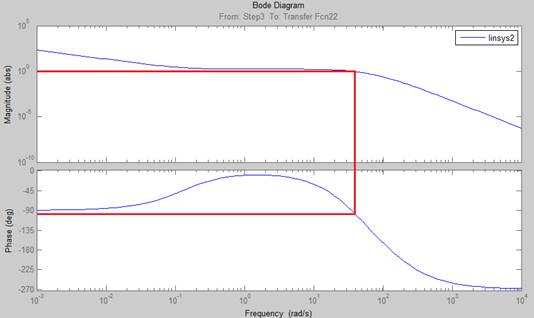
Рисунок 17. ЛАЧХ и ФЧХ ПИ регулятора
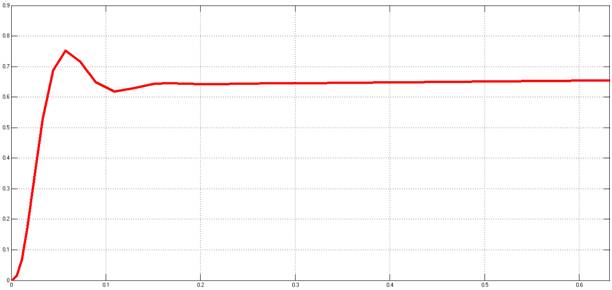
Рисунок 18. Переходный процесс относительно задающего воздействия
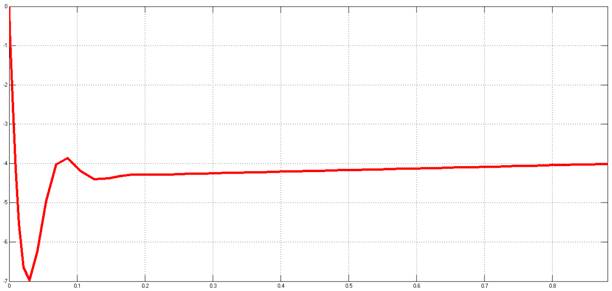
Рисунок 19. Переходный процесс относительно возмущающего воздействия
5.3.1 С учётом противо ЭДС двигателя
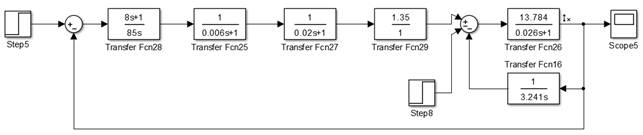
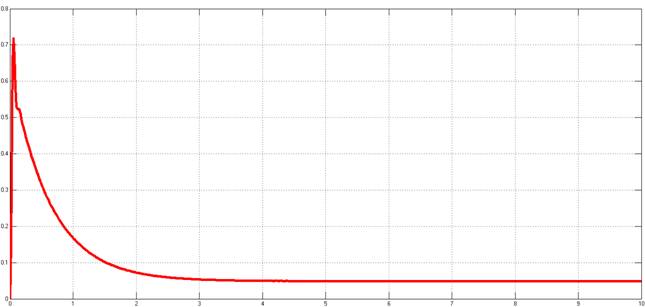
Рисунок 20. Переходный процесс относительно задающего воздействия с учётом противо ЭДС двигателя
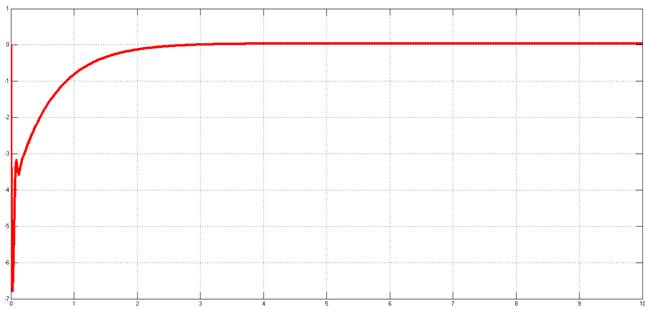
Рисунок 21. Переходный процесс относительно возмущающего воздействия с учётом противо ЭДС двигателя
Сравним эффективность некоторых корректирующих устройств последовательного типа по следующим параметрам δ – перерегулирование , hmax - максимальное значение выходной величины,tр – время регулирования, tmax - время достижения максимального значения,для наглядности данные сведем в таблицу.
Таблица 3
Показатели качества при задающем воздействии
|
Тип корректирующего устройства |
δ, % |
tр, с |
hmax |
hуст |
tmax, с |
|
Пропорциональное |
10 |
0,25 |
0,75 |
0,64 |
0,06 |
|
Интегрирующее |
8,97 |
0,7 |
1,18 |
1 |
0,2 |
|
Изодромное |
9 |
0,8 |
0,75 |
0,6 |
0,06 |
Таблица 4
Показатели качества при задающем воздействии с учётом противо ЭДС двигателя
|
Тип корректирующего устройства |
δ, % |
tр, с |
hmax |
hуст |
tmax, с |
|
Пропорциональное |
10 |
0,23 |
-7 |
-4,3 |
0,03 |
|
Интегрирующее |
10 |
0,7 |
-11 |
1 |
0,25 |
|
Изодромное |
10 |
0,8 |
-7 |
0,9 |
0,03 |
Таблица 5
Показатели качества при возмущающем воздействии
|
Тип корректирующего устройства |
δ, % |
tр, с |
hmax |
hуст |
tmax |
|
Пропорциональное |
100 |
6 |
0,72 |
0 |
0,1 |
|
Интегрирующее |
10 |
0,75 |
0,95 |
0,78 |
0,16 |
|
Изодромное |
100 |
0,8 |
0,72 |
0,05 |
0,1 |
Таблица 6
Показатели качества при возмущающем воздействии с учётом противо ЭДС двигателя
|
Тип корректирующего устройства |
δ, % |
tр, с |
hmax |
hуст |
tmax |
|
Пропорциональное |
100 |
3,5 |
-6,8 |
0 |
0,05 |
|
Интегрирующее |
10 |
0,8 |
-10 |
1 |
0,2 |
|
Изодромное |
100 |
4 |
-6,8 |
0 |
0,05 |
Проведя анализ таблиц мы выяснили, что наименьшую ошибку регулирования при задающем воздействии без учёта противо ЭДС – изодромное, с учётом – интегрирующее. Время регулирования наименьшее у пропорционального звена без учёта противо ЭДС, т.е. он обеспечивает наибольшее быстродействие системы.
6 Разгон двигателя с заданным ускорением
Выполним разгон двигателя с помощью блока ограничения, для этого рассчитаем параметры блока ограничения
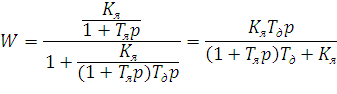
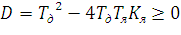
Откуда 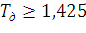 , из расчётов ранее
, из расчётов ранее
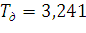 , следовательно, условие
выполняется.
, следовательно, условие
выполняется.
Рассчитаем электромеханическую постоянную времени
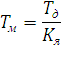
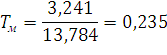
Рассчитаем ток якорной цепи
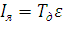
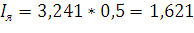
Рассчитаем напряжение на якоре max
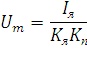
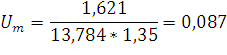
Итоговая схема контура регулирования тока якоря
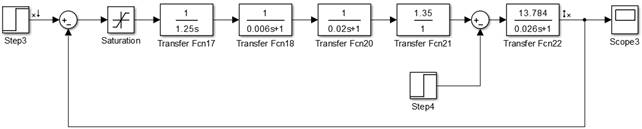
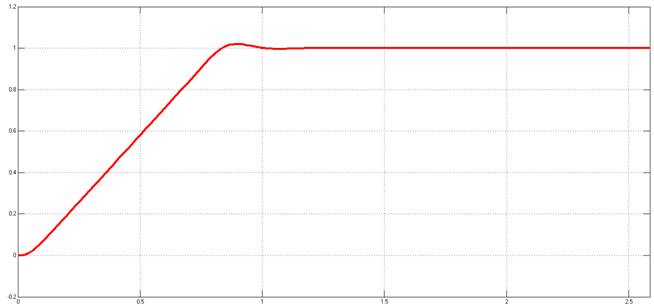
Рисунок 22. Переходный процесс разгона двигателя с БО
Из графика переходного процесса мы видим, что с заданным ускорением двигатель разгоняется за 1,2 секунды.
7 Статические характеристики контура регулирования тока с П и ПИ регуляторами
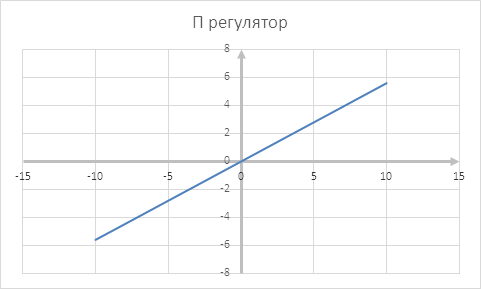
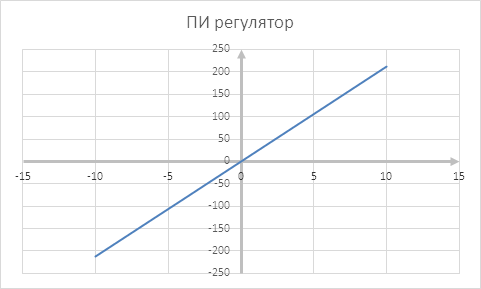
Библиографический список
1) Мацин В.П., Теория автоматического управления: учебное пособие к семестровому и курсовому проектированию. – Челябинск: Издательство ЮУрГУ, 2010 -25 с.
2) Гафиятуллин Р.Х., Маурер В.Г., Мацин В.П., Теория автоматического управления: учебное пособие. – Челябинск: Издательство ЮУрГУ, 2000 – 46 с.
3) Усынин Ю.С., Теория автоматического управления: учебное пособие для вузов. – Челябинск: Издательский центр ЮУрГУ, 2010 – 176 с.














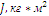
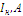
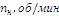
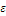
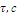
 (zip - application/zip)
(zip - application/zip)










