
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение
высшего профессионального образования
«Дальневосточный федеральный университет»
(ДВФУ)

инженерная Школа ДВФУ
КАФЕДРА АВТОМАТИЗАЦИИ И УПРАВЛЕНИЯ
КУРСОВАЯ РАБОТА
ПО ПРИКЛАДНОЙ МАТЕМАТИКЕ
НА ТЕМУ:
«Дискретная математика и математическая логика»
Выполнил студент группы Б3221
Коломиец А.Е.
Руководитель Васильева Т.В.
___________________________________
Дата защиты:
«____»_____________2015г.
Оценка: __________________________
Владивосток 2015
Оглавление
Введение
Задание 1
Задание 2
Задание
3
Задание
4
Задание
5
Задание
6
Задание
7
Список литературы
Введение
Дискретная математика - область математики, занимающаяся изучением дискретных структур, которые возникают как в пределах самой математики, так и в её приложениях.
В отличие от традиционной математики (математического анализа, линейной алгебры и др.), методы и конструкции которой имеют в основном числовую интерпретацию, дискретная математика имеет дело с объектами нечисловой природы: множествами, логическими высказываниями, алгоритмами, графами. Благодаря этому обстоятельству дискретная математика впервые позволила распространить математические методы на сферы и задачи, которые ранее были далеки от математики. Примером могут служить методы моделирования различных социальных и экономических процессов[1].
Задание 1
№1
а) Конечное множество – множество букв русского алфавита.
б) Бесконечное множество – множество вещественных чисел.
№2
а) Множество 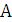 состоит из целых чисел (свойство) от
1 до 5.
состоит из целых чисел (свойство) от
1 до 5.
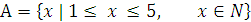
б) Множество – группа Б3221, которая состоит из студентов второго курса специальности «Мехатроника и Робототехника».
№3.
а) Гласные буквы являются подмножеством множества «алфавит».
б) Рациональные числа являются подмножеством множества вещественных чисел.
№4
а) Равные множества: 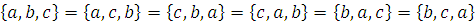
б) Равные множества: 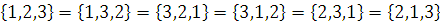
№5.
Рассмотрим множество 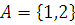 ,
,
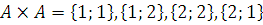
Определим бинарные отношения на этом множестве:
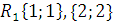 –
рефлексивно, симметрично, транзитивно, антисимметрично.
–
рефлексивно, симметрично, транзитивно, антисимметрично.
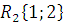 –
антирефлексивно.
–
антирефлексивно.
№6
Рассмотрим множество 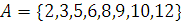 .
.
1)Данное множество транзитивно.
2)Рефлексивно.
3)Антисимметрично.
Найдем экстремальные
элементы множества 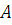 .
.
Минимальные элементы - 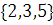 .
.
Максимальные элементы -
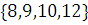 .
.
Задание 2
а) 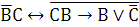
Таблица № 1 – таблица истинности.
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
Аналитически:
1)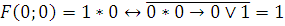
2)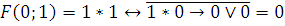
3)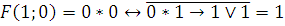
4)3)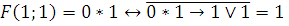
б)
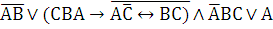
Таблица № 2 – таблица истинности.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
Аналитически:
1)
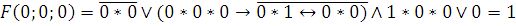
2)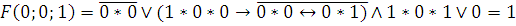
3)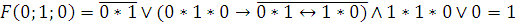
4)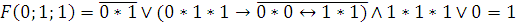
5)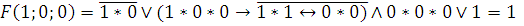
6)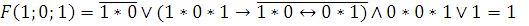
7)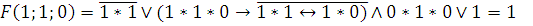
8)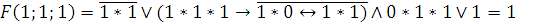
Задание 3
Проверить,
является ли система 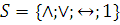
А)
Проверяем 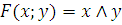
1) Функция, сохраняющая ноль.
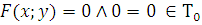
2) Функция, сохраняющая единицу.
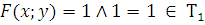
3) Самодвойственность –
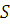 .
.
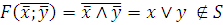
4)
Монотонность – 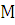 .
.
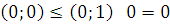
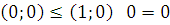
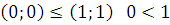
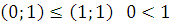
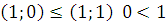
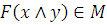
5) Линейность – 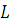 .
.
Представим 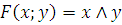 в
виде полинома Жегалкина.
в
виде полинома Жегалкина.
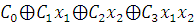
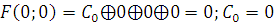
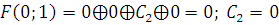
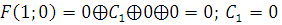
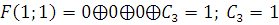
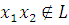
Б)
Проверяем 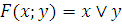
1) Функция, сохраняющая ноль.
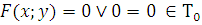
2) Функция, сохраняющая единицу.
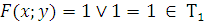
3)
Самодвойственность – 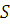 .
.
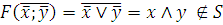
4) Монотонность – 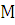 .
.
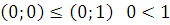
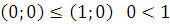
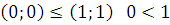
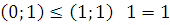
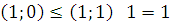
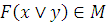
5) Линейность – 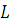 .
.
Представим 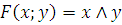 в
виде полинома Жегалкина.
в
виде полинома Жегалкина.
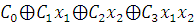
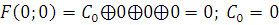
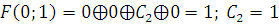
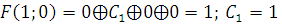
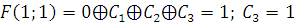
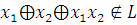
В) Проверяем 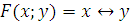
1) Функция, сохраняющая ноль.
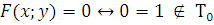
2) Функция, сохраняющая единицу.
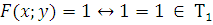
3)
Самодвойственность – 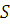 .
.
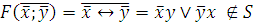
4)
Монотонность – 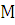 .
.
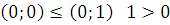
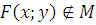
5) Линейность – 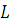 .
.
Представим 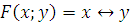 в
виде полинома Жегалкина.
в
виде полинома Жегалкина.
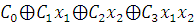
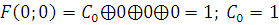
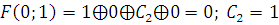
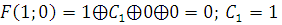
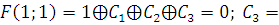
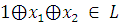
Г) Проверяем 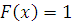
1) Функция, сохраняющая ноль.
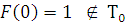
2) Функция, сохраняющая единицу.
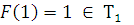
3) Самодвойственность –
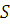 .
.
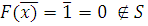
4) Монотонность – 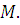
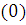 0
0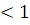
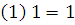
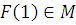
5) Линейность – L.
Представим 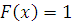 в
виде полинома Жегалкина.
в
виде полинома Жегалкина.
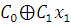
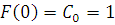
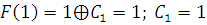
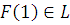
Таблица № 3 – таблица Поста.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система является не полной, добавим элементарную
функцию отрицание 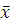 .
.
Таблица № 4 – таблица Поста.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система является полной, базис – {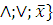
Задание 4
А)
1) Булева функция 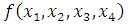 задана
вектором своих значений
задана
вектором своих значений 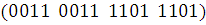 .
.
Запишем СДНФ данной функции:
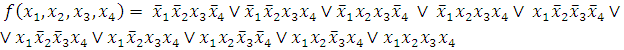
Первый этап – переход к сокращённой форме ДНФ.
Первая склейка:
(1-2) - 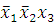
(1-3) -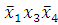
(2-4) - 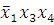
(2-7) - 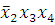
(3-4) - 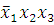
(4-10) - 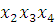
(5-6) - 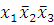
(5-8) - 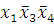
(6-7) - 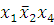
(7-10) - 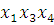
(8-9) - 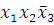
(9-10) - 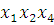
Вторая склейка:
(1-2)(3-4) - 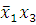
(1-3)(2-4) - 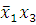
(1-3)(5-8) - 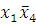
(2-7)(4-10) - 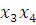
(2-4)(7-10) - 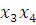
(5-6)(8-9) - 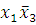
Сокращенная форма ДНФ:
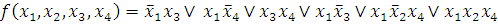
Найдем минимальную или тупиковую ДНФ.
Таблица № 5 - импликантная матрица.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
||||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
|
|
|
|
||||||||
|
|
|
|
Для получения минимальной формы достаточно выбрать из импликантов минимальное их число с минимальным количеством букв в каждом из этих импликант, которое обеспечит перекрытие всех столбцов.
Минимальная или тупиковая ДНФ
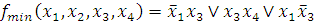
2)
Булева функция 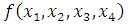 задана
вектором своих значений
задана
вектором своих значений 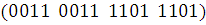 .
Найдем минимальную ДНФ с помощью карты Карно.
.
Найдем минимальную ДНФ с помощью карты Карно.
Таблица № 6 – карта Карно.
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Берём первую область и смотрим, какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных; если неменяющаяся переменная нулевая, проставляем над ней знак отрицания. Берём следующую область, выполняем то же самое, что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
В нашем случае:
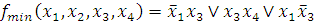
Б)
1)
Булева функция 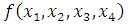 задана
вектором своих значений
задана
вектором своих значений 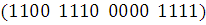 .
.
Запишем СДНФ данной функции:
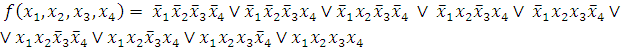
Переходим к сокращённой форме ДНФ.
Первая склейка:
(1-2)
- 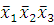
(1-3)
- 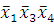
(2-4)
- 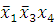
(3-4)
- 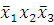
(3-5)
- 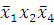
(3-6)
- 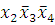
(4-7)
- 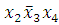
(5-8)
- 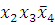
(6-7)
- 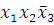
(6-8)
- 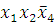
(7-9)
- 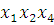
(8-9)
- 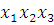
Вторая склейка:
(1-2)(3-4)
- 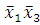
(1-3)(2-4)
- 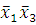
(3-4)(6-7)
- 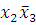
(3-5)(6-8)
- 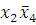
(4-7)(3-6)
- 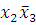
(5-8)(3-6)
- 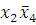
(6-7)(8-9)
- 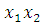
(6-8)(7-9)
- 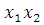
Сокращенная форма ДНФ:
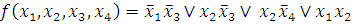
Найдем минимальную или тупиковую ДНФ.
Таблица № 6 - импликантная матрица.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Минимальная или тупиковая ДНФ:
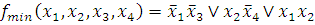
2)
Булева функция 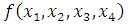 задана
вектором своих значений
задана
вектором своих значений 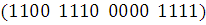 .
Найдем минимальную ДНФ с помощью карты Карно.
.
Найдем минимальную ДНФ с помощью карты Карно.
 Таблица
№ 7 – карта Корно.
Таблица
№ 7 – карта Корно.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Минимальная ДНФ:
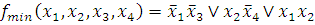
Задание 5
1) Пронумеруем вершины и дуги графа.
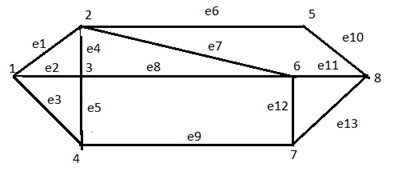
Рисунок 1 – граф
а) Матрица смежности:
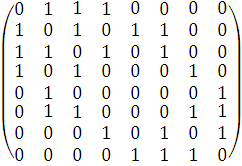
б) Матрица инцидентности:
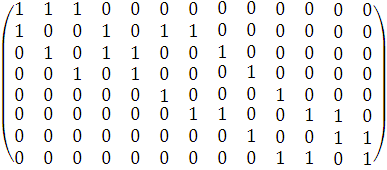
в) Список смежности:
|
Вершина |
Смежные вершины |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) Массив дуг:
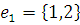
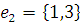
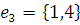
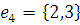
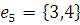
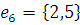
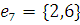
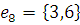
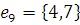
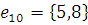
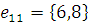
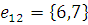
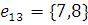
2) Найдем кратчайший остов графа с помощью Жадного алгоритма.
В этом алгоритме мы начинаем с пустого дерева и добавляем к нему ребра (без образования циклов) в порядке возрастания их весов пока не получим набор ребер, объединяющий все вершины графа.
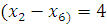
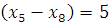
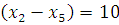
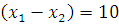
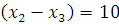
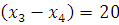
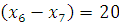
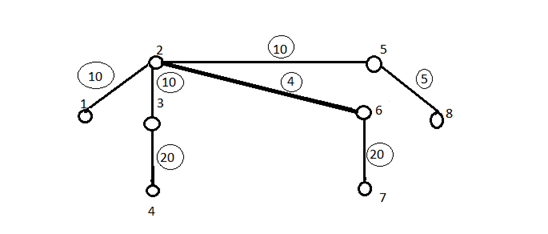
Рисунок 2 – остов графа
3) Найдем кратчайшее расстояние от вершины х1 до всех остальных вершин с помощью Алгоритма Дейкстры используя числа на ребрах.
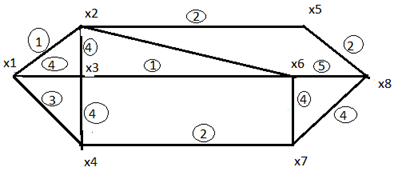
Рисунок 3 – взвешенный граф
Таблица № 8 – Алгоритм Дейкстры.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
||||
|
|
|
|
|||||
|
|
|
||||||
|
|
Имеем неориентированный взвешенный граф. Ищем кратчайшие пути от одной из вершин до остальных. Вершинам задаем так называемые "временные" и "постоянные" (квадратные скобки) метки. На каждом этапе наименьшая временная метка становится постоянной, от вершины с этой меткой на следующем этапе разыскиваются пути к доступным (соседним) вершинам.
4) Для найденного остова напишем матрицы циклов и разрезов.
а) Матрица циклов.
Мощность фундаментального множества циклов
равна цикломатическому числу 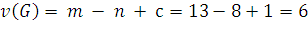
Ребра, входящие в остов дерева – дуги, а ребра, входящие в -дерево – хорды (обведены). Базисные циклы – пунктирная линия[2].
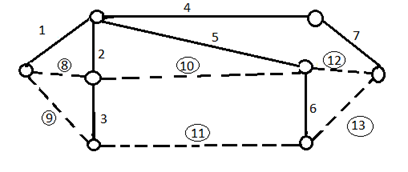
Рисунок 4 – остовное дерево с циклами.
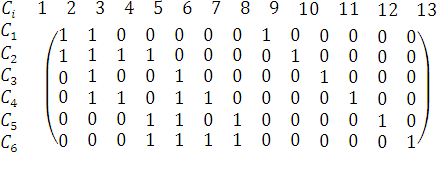
б) Матрица разрезов.
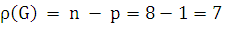 – количество базисных разрезов[2].
– количество базисных разрезов[2].
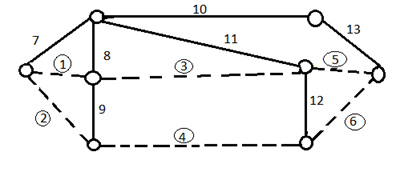
Рисунок 5 – остовное дерево с разрезами.
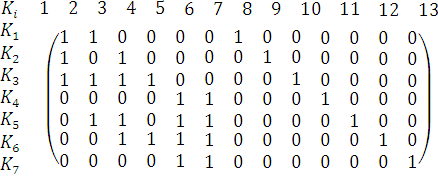
5) Наш граф не является Эйлеровым, потому что вершина 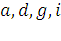 имеют степень
имеют степень 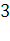 [3]. Добавим два ребра
[3]. Добавим два ребра 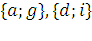
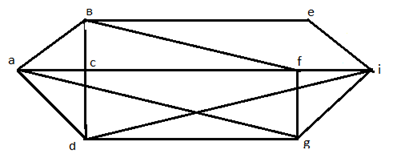
Рисунок 6 – Эйлеров граф.
6) Наш граф является Гамильтоновым, построим Гамильтоновы циклы[3].
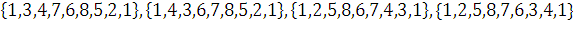
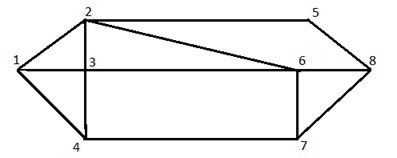
Рисунок 7 – Гамильтонов граф.
Задание 6
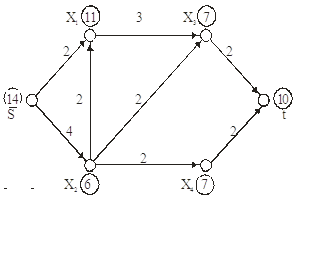 Найдем максимальный поток в сети:
Найдем максимальный поток в сети:
Рисунок 8 – сеть.
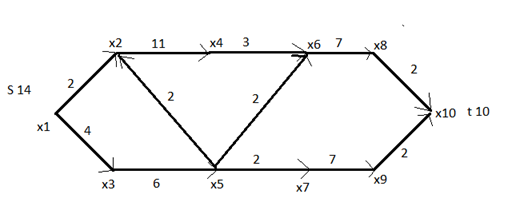
Рисунок 9 – сеть.
Первый этап:
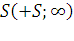
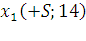
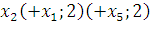
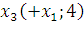
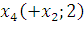
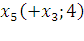
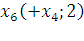
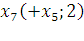
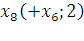
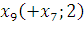
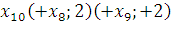
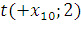
Второй этап:
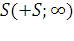
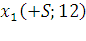
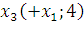
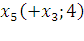
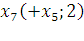
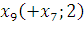
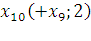
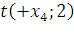
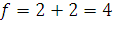 – максимальный поток в сети.
– максимальный поток в сети.
Минимальный разрез 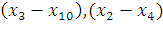
Вес минимального разреза 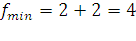
Задание 7
Методом математической индукции доказать, что для
любого 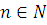
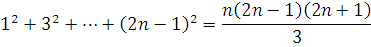
1) Базис
индукции 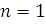
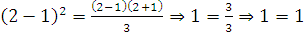 ,
верно
,
верно
2) Индуктивное
предположение 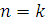
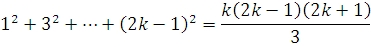
3) Индуктивный
переход 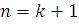
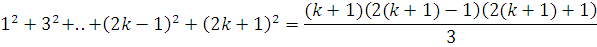
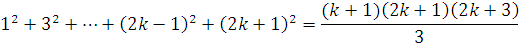
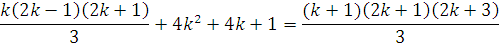
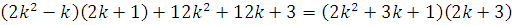
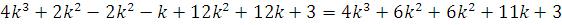
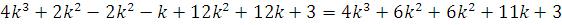
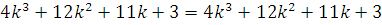 ,
что и требовалось доказать.
,
что и требовалось доказать.
Список литературы
1. Олег Кузнецов. Дискретная математика: информация [Электронный ресурс] : ИНТУИТ – национальный открытый институт - Электрон. дан. — Москва: 2015. — URL: http://www.intuit.ru/studies/courses/1049/317/info
2. Свами М., Тхуласираман К. Графы, сети и алгоритмы. [Электронный ресурс] : М.: Мир, 1984 – URL: http://stu.alnam.ru/book_grnet-46
3. Б.М.Верников, А.М.Шур. Лекция 4: Эйлеров и гамильтонов цикл [Электронный ресурс] : Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики : 2015 – URL: http://kadm.imkn.urfu.ru/files/tgr04.pdf














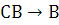
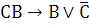
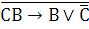
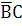
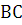
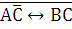
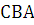
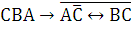
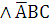
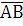
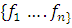
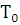
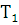
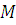
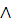
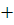



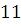
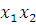

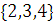
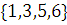
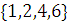
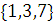
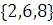
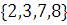
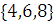
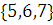
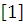
 (zip - application/zip)
(zip - application/zip)










