Деформовані дужки Пуассона

Міністерство освіти і науки України

Львівський національний університет імені Івана Франка

Кафедра теоретичної фізики

Зміст

1.     Вступ ……………………………………………………………..…2

2.     Деформовані дужки Пуассона……………………………………..3

3.     Рух в центральному полі гамільтоніана частинки кулонівського потенціалу…………………………………………………....……..4

4.     Рух в кулонівському потенціалі……………………………….......5

5.     Кут прецесії…………………………………………………………8

6.     Висновок ………………………………………………….……….12

7.     Список використаної літератури…………………………………13

Вступ

Завданням  даної роботи є визначення кута прецесії частинки кулонівського потенціалу, для цього  ми розглянемо класичну задачу Кеплера зі збуренням, замінивши класичну дужку Пуассона на деформовану ,при цьому використавши таку умову.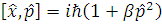

Для гамільтоніана 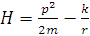   покажемо, що лагранжіан  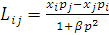 є інтеграл руху для центрального поля, тобто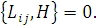

Запишемо рівняння траєкторії для нашої системи в сферичних координатах. Визначимо максимальний і мінімальни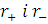й  радіуси орбіти частинки.

Визначимо кут прецесії орбіти частинки в лінійному по параметрах деформації наближенні.

 1. Деформовані дужки Пуассона

Класична задача

У D- вимірах, деформовану алгебру Гайзенберга можна виразити в тензорній формі

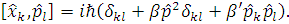
Припустимо, що компоненти моменту 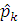 комутують один з одним

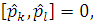
тоді комутаційні співвідношення серед координат 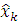 майже однозначно визначається тотожністю Якобі, як

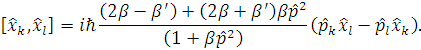
У класичній границі квантово-механічний комутатор замінюється дужкою Пуассона

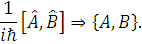
Так у класичній границі деформовану алгебру Гайзенберга ми перепишемо через дужки Пуассона

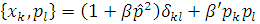
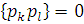
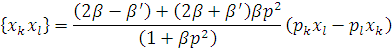
Ми отримуємо параметри 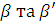 зафіксовані при 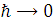, поки значення довжини взяте за нуль.Вимагаючи щоб дужка Пуассона задовільнила їх властивості, тобто повинна бути антисиметрія і білінійність, задовольняти привила Лейбніца та тотожність Якобі. Запишемо загальну форму нашої дужки Пуассона будь-якої функції координат і моменту імпульсу

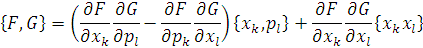
Де є повторне підсумовування по індексах, еволюція в часі координати та імпульса

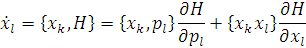
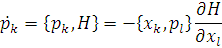
2. Рух в центральному полі

Для гамільтоніана

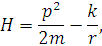
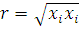
Покажемо, що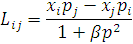

 інтегралом руху для центрального поля,

,

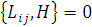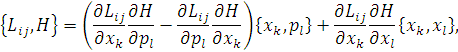
візьмемо похідні по координатах та імпульсах і підставимо в рівняння,

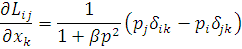
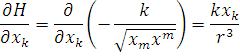
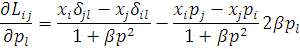
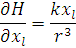
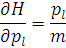
Отримаємо

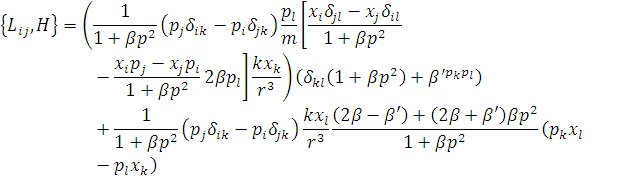
Зробивши деякі перетворення і підставивши в рівність

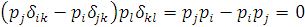
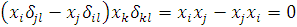
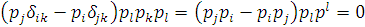
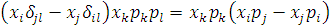
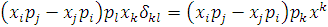
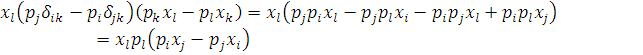
 маємо

3. Рух в кулонівському потенціалі.

Запишемо рівняння траєкторії:

Перейдемо до сферичних координат

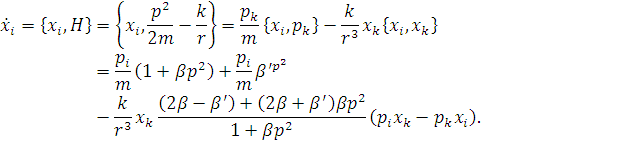
де рівняння руху для r задається:

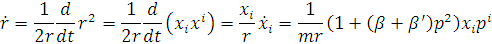
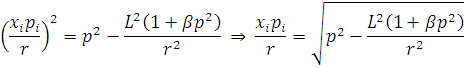
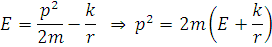
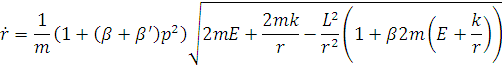
для :

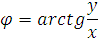
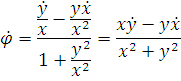
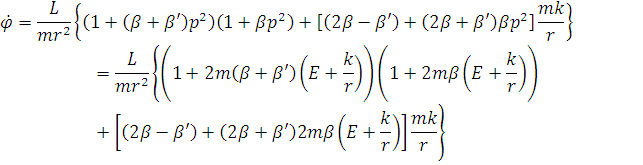
Отримаємо рівняння траєкторії

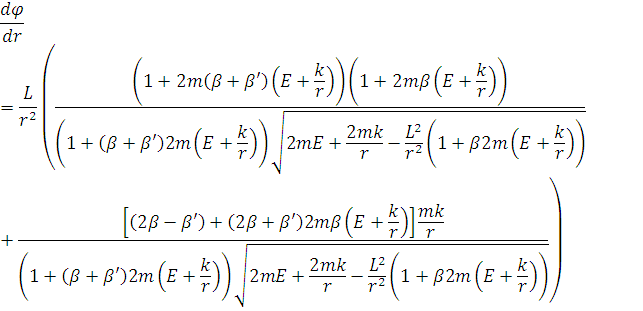
Визначимо максимальний і мінімальний радіус 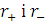 з рівняння траєкторії.

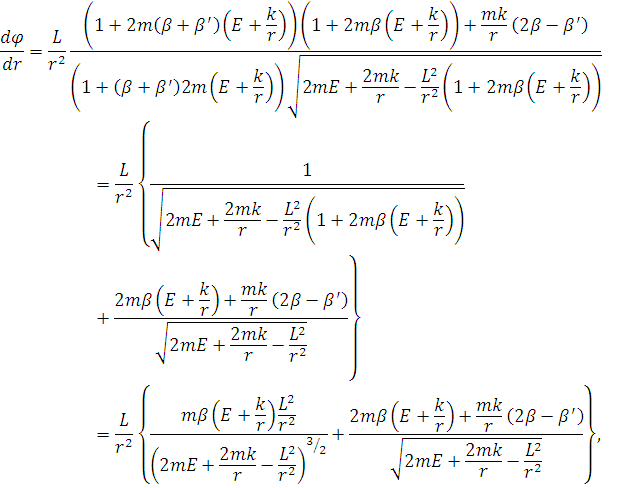
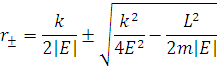
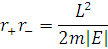
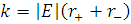
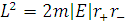
4. Кут прецесії

Знайдемо кут прецесії орбіти частинки в лінійному по параметрах деформації наближенні. Розіб’ємо рівняння траєкторії на два рівняння і проінтегруємо їх.

Розглянемо друге рівняння

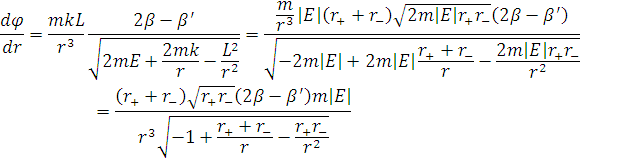
проінтегрувавши це рівняння отримаємо

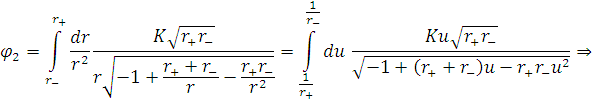
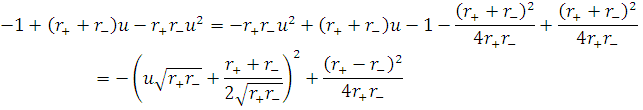
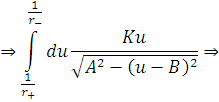
Де                               

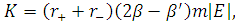
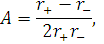
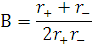
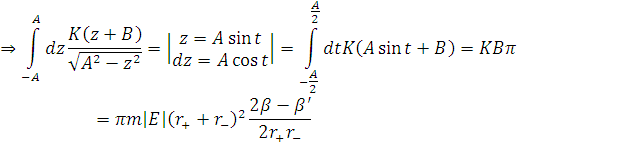
Тепер розглянемо перше рівняння

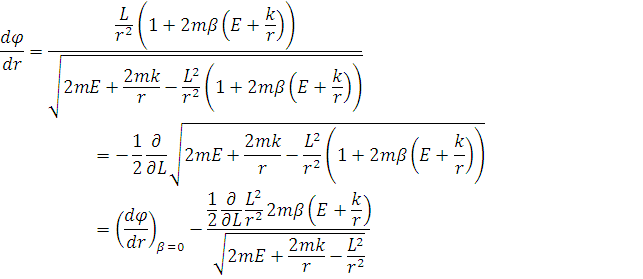
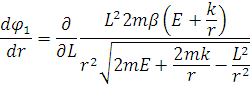
проінтегрувавши яке маємо

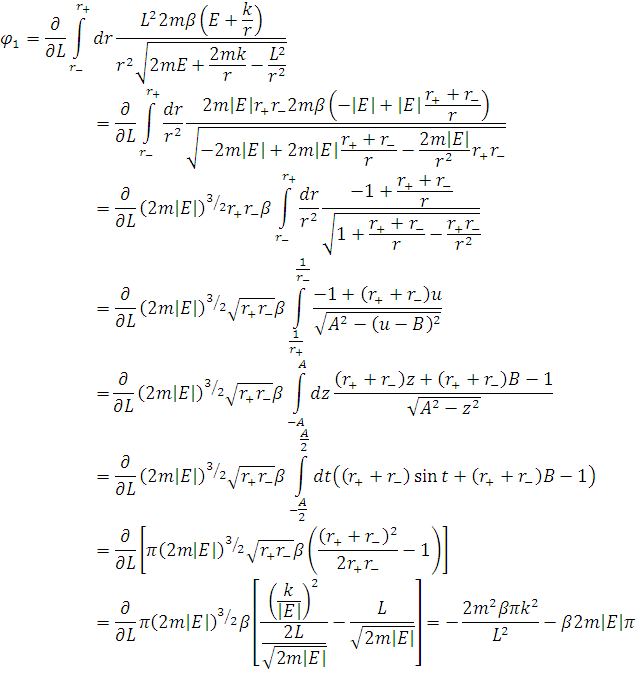
Кут прецесії 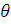 визначається за таким співвідношенням

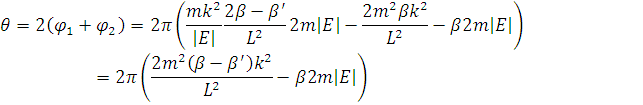
Зобразимо на рисунках траєкторію руху кулонівської частинки з параметрами  ,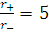

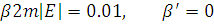
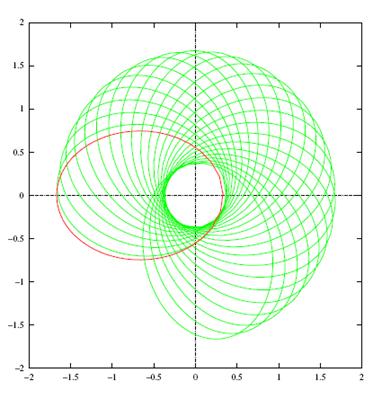
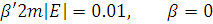
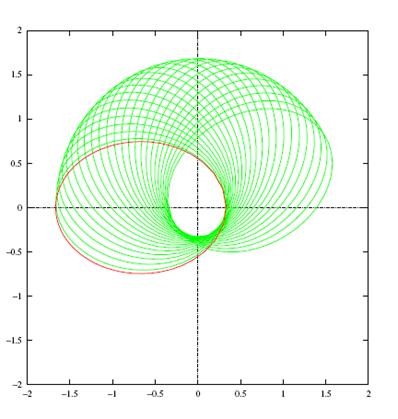
Висновок.

Розглянуто кеплерівську проблему в просторі деформованою алгеброю Гайзенберга. Знайдено деформований момент імпульсу, який є інтегралом руху. Записано рівняння руху в даному потенціалі. Знайдено кут прецесії орбіти частинки в лінійному по параметрах деформації наближенні.

Список використаної літератури:

1. Інтернет ресурс- http://xxx.lanl.gov/pdf/hep-th/0204049.pdf.

2. М.Т Сеньків «ВЕКТОРНИЙ І ТЕН3ЗОРНИЙ АНАЛІЗ» Львів 1991р.