Автономное общеобразовательное учреждение высшего профессионального образования

Курская академия государственной и муниципальной службы

Кафедра «Информационной и техносферной безопасности и правовой защиты информации»

РЕФЕРАТ

по дисциплине «Методы оптимальных решений»

на тему «ДВУХФАЗНЫЙ СИМПЛЕКС-МЕТОД»

Выполнила: Михеева Ольга

студентка 2 курса

специальности «Экономика»

Проверил: Погосян Сергей Левонович, к.ф.м.н., доцент

Курск – 2012

Оглавление

Введение. 3

1. Симплекс-метод. 4

1.1. Понятие симплекс-метода. 4

1.2. Идея симплекс-метода. 6

1.3. Алгоритм симплекс-метода. 8

2. Двухфазный симплекс-метод. 11

2.1. Содержание двухфазного симплекс-метода. 11

2.2. Фазы решения задач. 12

Заключение. 17

Список использованной литературы.. 18

      

Введение

В последние годы в прикладной математике большое внимание уделяется новому классу задач оптимизации, заключающихся в нахождении в заданной области точек наибольшего или наименьшего значения некоторой функции, зависящей от большого числа переменных. Это так называемые задачи математического программирования, возникающие в самых разнообразных областях человеческой деятельности и прежде всего в экономических исследованиях, в практике планирования и организации производства («Определение наилучшего состава смеси», «Задача об оптимальном плане выпуска продукции», «Оптимизация межотраслевых потоков», « Задача о диете», «Транспортная задача» и т.д.).

Линейное программирование - это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения. Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции. Казалось бы, что для исследования линейной функции многих переменных на условный экстремум достаточно применить хорошо разработанные методы математического анализа, однако невозможность их использования можно довольно просто проиллюстрировать.

1. Симплекс-метод

1.1. Понятие симплекс-метода

В общем виде, когда в задаче участвуют N-неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в n-мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах. Решить данные задачи графически, когда количество переменных более 3 весьма затруднительно. Существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.      

Симплекс-метод является основным в линейном программировании. Решение задачи начинается с рассмотрений одной из вершин многогранника условий. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней, увеличивая значение функции цели при решении задачи на максимум и уменьшая при решении задачи на минимум. Таким образом, переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима.

Этот метод является универсальным, применимым к любой задаче линейного программирования в канонической форме. Система ограничений здесь - система линейных уравнений, в которой количество неизвестных больше количества уравнений. Если ранг системы равен r, то мы можем выбрать r неизвестных, которые выразим через остальные неизвестные. Для определенности предположим, что выбраны первые, идущие подряд, неизвестные X₁, X₂, ..., X_r. Тогда наша система уравнений может быть записана как

 К такому виду можно привести  любую совместную систему, например, методом Гаусса. Правда, не всегда можно выражать через остальные первые r неизвестных (мы это сделали для определенности записи). Однако такие r неизвестных обязательно найдутся. Эти неизвестные (переменные) называются базисными, остальные свободными.

Симплекс-метод основан на теореме, которая называется фундаментальной теоремой симплекс-метода. Среди оптимальных планов задачи линейного программирования в канонической форме обязательно есть опорное решение ее системы ограничений. Если оптимальный план задачи единственен, то он совпадает с некоторым опорным решением. Различных опорных решений системы ограничений конечное число. Поэтому решение задачи в канонической форме можно было бы искать перебором опорных решений и выбором среди них того, для которого значение F самое большое. Но, во-первых, все опорные решения неизвестны и их нужно находить, a, во-вторых, в реальных задачах этих решений очень много и прямой перебор вряд ли возможен. Симплекс-метод представляет собой некоторую процедуру направленного перебора опорных решений. Исходя из некоторого, найденного заранее опорного решения по определенному алгоритму симплекс-метода мы подсчитываем новое опорное решение, на котором значение целевой функции F не меньше, чем на старом. После ряда шагов мы приходим к опорному решению, которое является оптимальным планом.

 

 

1.2. Идея симплекс-метода

Итак, симплексный метод вносит определенный порядок как при нахождении первого (исходного) базисного решения, так и при переходе к другим базисным решениям. Его идея состоит в следующем.

Имея систему ограничений, приведенную к общему виду, то есть к системе m линейных уравнений с n переменными (m < n), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то, осуществляется переход к другому, обязательно допустимому базисному решению.

Симплексный метод гарантирует, что при этом новом решении линейная форма, если и не достигнет оптимума, то приблизится к нему. С новым допустимым базисным решением поступают так же, пока не находят решение, которое является оптимальным. Если первое найденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляется переход к другим базисным решениям, которые приближают нас к области допустимых решений, пока на каком-то шаге решения либо базисное решение окажется допустимым и к нему применяют алгоритм симплексного метода, либо мы убеждаемся в противоречивости системы ограничений.

Таким образом, применение симплексного метода распадается на два этапа: нахождение допустимого базисного решения системы ограничений или установление факта ее несовместности; нахождение оптимального решения. 
При этом каждый этап может включать несколько шагов, соответствующих тому или иному базисному решению. Но так как число базисных решений всегда ограниченно, то ограниченно и число шагов симплексного метода.

Приведенная схема симплексного метода явно выражает его алгоритмический характер (характер четкого предписания о выполнении последовательных операций), что позволяет успешно программировать и реализовать этот метод на ЭВМ. Задачи же с небольшим числом переменных и ограничений могут быть решены симплексным методом вручную.

Не останавливаясь подробнее на сути алгоритма, опишем его вычислительную сторону. Вычисления по симплекс-методу организуются в виде симплекс-таблиц, которые являются сокращенной записью задачи линейного программирования в канонической форме. Перед составлением симплекс-таблицы задача должна быть преобразована, система ограничений приведена к допустимому базисному виду, c помощью которого из целевой функции должны быть исключены базисные переменные. Вопрос об этих предварительных преобразованиях мы рассмотрим ниже. Сейчас же будем считать, что они уже выполнены и задача имеет вид:

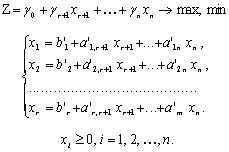
Здесь для определенности записи считается, что в качестве базисных переменных можно взять переменные X₁, X₂, ..., X_r и что при этом b₁, b₂,..., b_r ≥ 0 (соответствующее базисное решение является опорным).

Для составления симплекс-таблицы во всех равенствах в условии задачи члены, содержащие переменные, переносятся в левую часть, свободные оставляются справа, т.е. задача записывается в виде системы равенств:

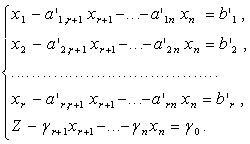
Далее эта система оформляется в виде симплекс-таблиц:

1.3. Алгоритм симплекс-метода

Теперь приведём шаги алгоритма. На каждом шаге мы будем менять множества простых и непростых векторов (двигаться по рёбрам), и матрица будет иметь следующий вид:

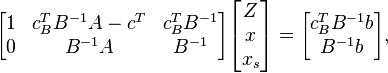
где c_B — коэффициенты вектора c соответствующие простым переменным (переменным x_s соответствуют 0), B — столбцы, соответствующие простым переменным. Матрицу, образованную оставшимися столбцами обозначим D. Почему матрица будет иметь такой вид поясним в описании шагов алгоритма.

Первый шаг

Выбираем начальное допустимое значение, как указано выше. На первом шаге B — единичная матрица, так как простыми переменными являются x_s. c_B — нулевой вектор по тем же причинам.

Второй шаг

Покажем, что в выражении 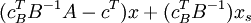 только непростые переменные имеют ненулевой коэффициент. Заметим, что из выражения Ax+x_s=b простые переменные однозначно выражаются через непростые, так как число простых переменных равно числу уравнений. Пусть x " — простые, а x " " — непростые переменные на данной итерации. Уравнение Ax+x_s=b можно переписать, как Bx "+Dx " "=b. Умножим его на  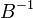слева: 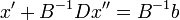. Таким образом мы выразили простые переменные через непростые, и в выражении 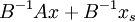, эквивалентному левой части равенства, все простые переменные имеют единичные коэффициенты. Поэтому, если прибавить к равенству  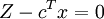равенство 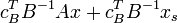, то в полученном равенстве все простые переменные будут иметь нулевой коэффициент — все простые переменные вида x сократятся, а простые переменные вида x_s не войдут в выражение .

Выберем ребро, по которому мы будем перемещаться. Поскольку мы хотим максимизировать Z, то необходимо выбрать переменную, которая будет более всех уменьшать выражение

.

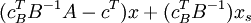Для этого выберем переменную, которая имеет наибольший по модулю отрицательный коэффициент. Если таких переменных нет, то есть все коэффициенты этого выражения неотрицательны, то мы пришли в искомую вершину и нашли оптимальное решение. В противном случае начнём увеличивать эту непростую переменную, то есть перемещаться по соответствующему ей ребру. Эту переменную назовём входящей.

Третий шаг

Теперь необходимо понять, какая простая переменная первой обратится в ноль по мере увеличения входящей переменной. Для этого достаточно рассмотреть систему:

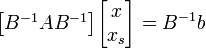
При фиксированных значениях непростых переменных система однозначно разрешима относительно простых, поэтому мы можем определить, какая из простых переменных первой достигнет нуля при увеличении входящей. Эту переменную назовем выходящей. Это будет означать, что мы натолкнулись на новую вершину. Теперь входящую и выходящую переменную поменяем местами — входящая «войдёт» в простую, а выходящая из них «выйдет» в непростые. Теперь перепишем матрицу B и вектор c_B в соответствии с новыми наборами простых и непростых переменных, после чего вернёмся ко второму шагу. x""

Поскольку число вершин конечно, то алгоритм однажды закончится. Найденная вершина будет являться оптимальным решением.

2. Двухфазный симплекс-метод

 

2.1. Содержание двухфазного симплекс-метода

Двухфазный симплекс-метод (или метод искусственного базиса) применяется в тех случаях, когда в задаче ЛП в канонической форме затруднительно определить начальное допустимое базисное решение с помощью элементарных преобразований (привести систему к диагональному виду). 

Если в условии задачи линейного программирования не все ограничения представлены неравенствами типа «≤», то далеко не всегда нулевой вектор будет допустимым решением. Однако каждая итерация симплекс-метода является переходом от одной вершины к другой, и если неизвестно ни одной вершины, алгоритм вообще не может быть начат.

Процесс нахождения исходной вершины не сильно отличается от однофазного симплекс-метода, однако может в итоге оказаться сложнее, чем дальнейшая оптимизация.

Все ограничения задачи модифицируются согласно следующим правилам:

·         ограничения типа «≤» переводятся на равенства созданием дополнительной переменной с коэффициентом «+1». Эта модификация проводится и в однофазном симплекс-методе, дополнительные переменные в дальнейшем используются как исходный базис.

·         ограничения типа «≥» дополняются одной переменной с коэффициентом «−1». Поскольку такая переменная из-за отрицательного коэффициента не может быть использована в исходном базисе, необходимо создать ещё одну, вспомогательную, переменную. Вспомогательные переменные всегда создаются с коэффициентом «+1».

·         ограничения типа «=» дополняются одной вспомогательной переменной.

 Соответственно, будет создано некоторое количество дополнительных и вспомогательных переменных. В исходный базис выбираются дополнительные переменные с коэффициентом «+1» и все вспомогательные. Осторожно: решение, которому соответствует этот базис, не является допустимым.

Несмотря на то, что и дополнительные, и вспомогательные переменные создаются искусственно и используются для создания исходного базиса, их значения в решении сильно отличаются:

·         дополнительные переменные сообщают, насколько соответствующее им ограничение «недоиспользовано». Значение дополнительной переменной, равное нулю, соответствует равенству значений правых и левых частей ограничения.

·         вспомогательные переменные сообщают, насколько данное условие далеко от допустимого (относительно конкретного ограничения). Если значение вспомогательной переменной больше нуля, то данное решение не выполняет определённое ограничение, а значит не является допустимым.

То есть ненулевое значение дополнительной переменной может (но не должно) сигнализировать о неоптимальности решения. Ненулевое значение вспомогательной переменной сигнализирует о недопустимости решения.

2.2. Фазы решения задач

Рассмотрим фазы решения задачи двухфазным симплекс-методом на конкретном примере.

Пример. Следующую задачу ЛП решить двухфазным симплекс-методом: 
f(x) = x₁ – x₂ + 1 → min                                   
при ограничениях

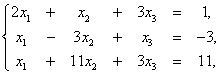
x₁, x₂, x₃ ≥ 0           

при ограничениях:

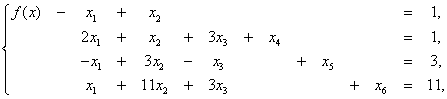
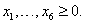
Искусственные переменные x₄, x₅, x₆,выбираем в качестве базисных, а все остальные x₁, x₂, x₃ - в качестве небазисных. По правилу симплекс-метода исключаем базисные переменные из целевой функции, содержащих эти переменные): 
 
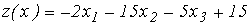
или, что все равно,

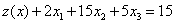
Начальное допустимое базисное решение 
 
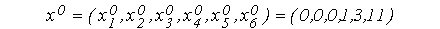
называется искусственным базисом. При помощи этого базиса и выражений , (строим начальную симплекс-таблицу I-ой фазы. 
 
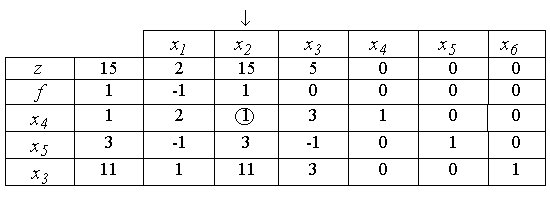
      До конца первой фазы роль нулевой строки играет строка z , все остальное – как в симплекс-методе. Следует только заметить, что строка для f(x) не участвует в выборе ведущей строки. 
Видно, что min z(x)=0 и достигается при x₄=x₅=x₆=0, т.е. задача будет решена, если все искусственные переменные будут вытеснены из базиса, а z=0 . Это и будет означать конец первой фазы и переход ко второй фазе. 
      Обратите внимание, что в первой таблице ведущей может быть любая из последних трех строк (предвестник зацикливания). В таких случаях можно выбрать любой из них - выберем первую строку. 
Так как искусственная переменная x₄ выходит из базиса, то соответствующий столбик в дальнейшем можно исключить. 
В результате соответствующих преобразований получим вторую симплекс-таблицу. 
 
     Из таблицы следует, что min z достигнут, однако искусственные переменныеx₆и x₅ еще не выведены из базиса. В такой ситуации правила симплекс-метода "не работают" (так как ввиду отсутствия в нулевой строке положительных оценок нельзя выбрать ведущий столбик).

Задача здесь одна - вывести оставшиеся искусственные переменные из базиса. Выведем сначала x₅. Умножим все элементы этой строки на -1 (что допустимо, так как в нулевом столбике стоит 0). Введем в базис вместо x₅ переменную x₁ . С этой целью строку для x₅ поделим на 7 и с "ведущим элементом" 1 выполним элементарные преобразования (как в симплекс-методе). В результате получим таблицу: 
 
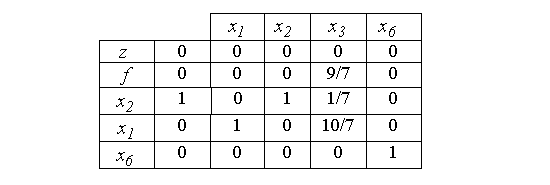
     Остается в базисе еще x₆ . Ее из числа базисных вывести нельзя, так как все элементы этой строки равны нулю, кроме 1 в столбике для x₆. Это говорит о том, что в системе третье уравнение было "лишним", и потому последнюю строку таблицы можно вычеркнуть. Действительно, третье уравнение является линейной комбинацией первых двух (оно получается вычитанием второго уравнения, умноженного на 3, из первого уравнения, умноженного на 2). 
     Вычеркивая столбик x₆ и строку для z , приходим к таблице 
 
содержащей только элементы исходной задачи и с базисными переменными из числа исходных переменных. Таким образом, цель первой фазы  выполнена. 
Вторая фаза(цель: применяя обычный симплекс-метод к полученной в результате первой фазы таблице, получить оптимальное решение исходной задачи). 
     Допустимое базисное решение для последней таблицы есть x⁰=(0,1,0) . Заметим, что это вырожденное д.б.р., так как в нем базисная переменная x₁=0, т.е. здесь мы можем получить зацикливание. 
     Теперь можно привести алгоритм двухфазного симплекс-метода: 
1. привести задачу ЛП к канонической форме; 
2. ввести в ограничения искусственные переменные и составить новую целевую функцию z ; 
3. исключить из новой целевой функции все искусственные переменные; 
4. используя искусственные переменные в качестве базисных, построить начальную симплекс-таблицу; 
5. применить симплекс-метод, исключая из таблиц столбцы для искусственных переменных по мере их выхода из базиса до тех пор, пока min z=0 и все искусственные переменные не будут выведены из базиса; 
6. вычеркнуть строчку для z и перейти ко второй фазе; 
7. во второй фазе к таблице, полученной в результате первой фазы, применять симплекс-метод до тех пор, пока не найдется оптимальное решение исходной задачи или не выявится его отсутствие. 
      Примечания к двухфазному симплекс-методу.
1. Если в результате первой фазы окажется, что min z>0, то система ограничений исходной задачи (в канонической форме) несовместна. Во всех остальных случаях первая фаза разрешима. 
2. Если min z=0 и в таблице остались искусственные переменные, то, используя элементарные преобразования, эти переменные следует вывести из базиса, а вместо них ввести исходные переменные. 
3. Пусть каноническая форма задачи ЛП получена с помощью слабых переменных. Применение двухфазного симплекс-метода упростится, если искусственные переменные ввести только в те ограничения, в которых слабая переменная либо отсутствует (исходное ограничение - равенство), либо не может войти в базис (введена в ограничение со знаком минус).

Заключение

 Рис. 3

Симплекс-метод является основным в линейном программировании. Решение задачи начинается с рассмотрений одной из вершин многогранника условий. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней, увеличивая значение функции цели при решении задачи на максимум и уменьшая при решении задачи на минимум. Таким образом, переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима.

Этот метод является универсальным, применимым к любой задаче линейного программирования в канонической форме. Система ограничений здесь - система линейных уравнений, в которой количество неизвестных больше количества уравнений.

Список использованной литературы

1.     Большакова И. В., Кураленко М. В. «Линейное программирование. Учебно-методическое пособие к контрольной работе.

2.     Барсов А. С. «Что такое линейное программирование», Популярные лекции по математике, Гостехиздат, 1959.

3.     Хемди А. Таха Введение в исследование операций

4.     http://ru.wikipedia.org/

5.     http://referat.ru/

6.     http://math.semestr.ru/simplex/lpsimplex2.php