Численные методы решения дифференциальных уравнений

Министерство образования и науки Российской Федерации

Санкт-Петербургский государственный архитектурно-строительный

университет

Кафедра прикладной математики и информатики

Курсовая работа

По теме: «Численные методы решения дифференциальных уравнений»

Вариант №7

Выполнила магистрант гр. 2-См-1:

П.М. Гурьева

Принял проф., д.ф.-м.н.:

Б.Г.Вагер

Санкт-Петербург

2016

Оглавление

Задача №1. 3

Задача №2. 12

Выводы.. 16

Задача №1

Дано:

,

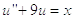
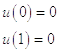
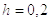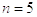
Необходимо:

а)       решить краевую задачу методом конечных разностей;

б)      методом Ритца;

в)       методом Бубнова-Галеркина.

Полученные результаты сравнить.

Решение

Метод конечных разностей

Является наиболее распространённым методом интегрирования дифференциальных уравнений. Решение проводится в 4 этапа:

·          введение разностной сетки;

·          необходимо написать разностный аналог дифференциального уравнения во внутренних узлах сетки;

·          записать начальные и краевые условия;

·          решения конечно-разностной системы уравнений методом прогонки.

Из условия уравнения находим необходимые компоненты:

, ,

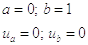
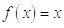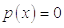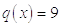
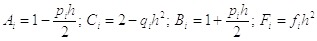
Дальнейшее решение ведем в виде таблицы.

Таблица 1

Записываем системы уравнений.

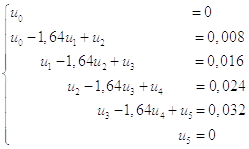
Формулы для решения системы уравнений методом прогонки:

·        прямой ход

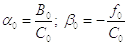
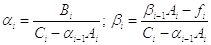
·        обратный ход .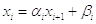

Прямой ход:

1)     

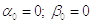
2)     

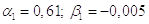
3)     

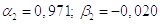
4)     

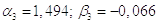
5)     

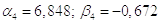
6)     

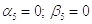
Обратный ход:

1)     

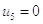
2)     

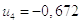
3)     

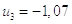
4)     

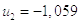
5)     

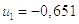
6)     

Проверка:

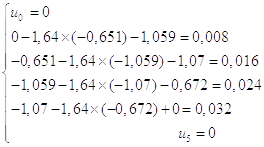
Метод Ритца

,

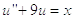
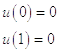
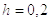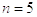
Необходимые компоненты:

, ,

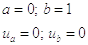
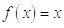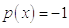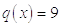
Выбираем систему координатных функций:

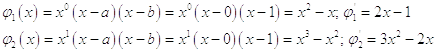
Приближение решения задачи ищется в виде:

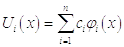
где 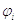 уже получены, а коэффициенты  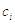находятся из условий минимизации функционала:

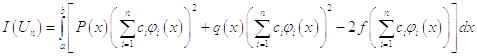
Для нахождения минимума функционала нужно взять частные производные и приравнять их к нулю:

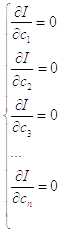
Так как 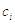 входит в функционал в квадрате, то система, приведенная выше, - это система линейных алгебраических уравнений, которую можно записать в матричном виде:

,

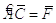где 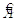 - симметричная матрица квадратичной формы (),

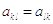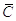 - искомый вектор,

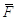 - известный вектор правых частей.

Первое приближение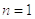

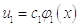
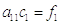
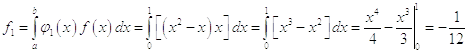
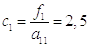
В первом приближении получили уравнение:

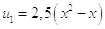
Второе приближение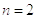

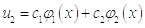
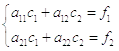
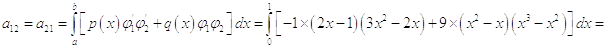
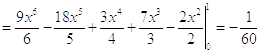
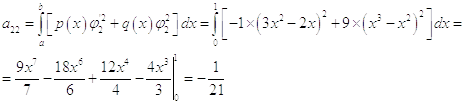
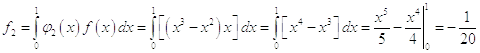
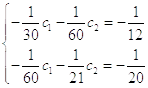
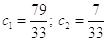
Во втором приближении получили уравнение:

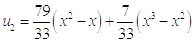
Произведем сравнение результатов, полученных из уравнений первого и второго приближений.

Таблица 2

Метод Бубнова-Галеркина

,

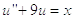
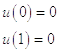
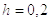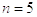
Необходимые компоненты:

,

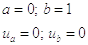
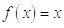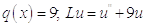
Выбираем систему координатных функций:

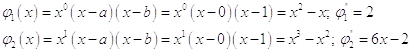
Составим невязку .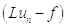

Если 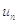 - точное решение, то невязка равна нулю. Будем требовать, чтобы невязка была ортогональна всем 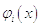, т.е.  ().

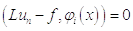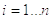Данное условие можно записать в виде:

 

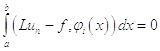
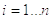
Этот функционал запишем в следующем виде:

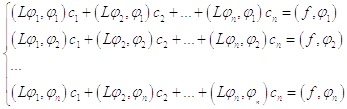
Первое приближение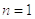

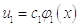
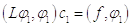
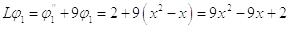
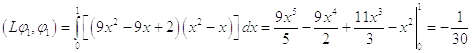
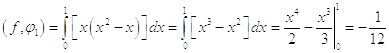
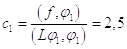
В первом приближении получили уравнение:

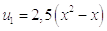
Второе приближение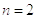

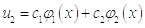
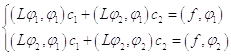
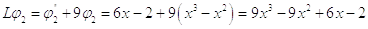
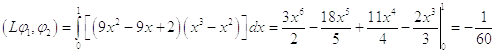
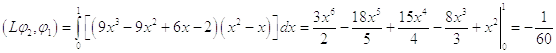
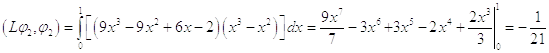
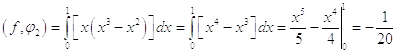
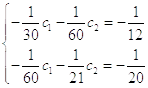
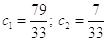
Во втором приближении получили уравнение:

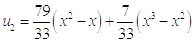
Произведем сравнение результатов, полученных из уравнений первого и второго приближений.

Таблица 3

Решения краевой задачи методом Ритца и методом Бубнова-Галеркина дали одинаковые результаты. Следовательно, можно сделать вывод, что оба метода являются эффективными.

Задача №2

Дано:

,

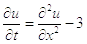
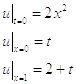
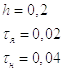
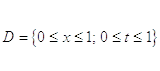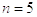
Найти: Необходимо сделать 6 шагов расчетов по явной схеме решения уравнения и 3 шага по неявной схеме. Результаты сравнить.

Решение

Явная схема

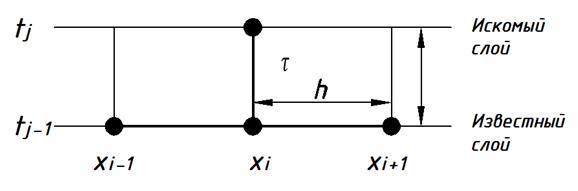
Рис. 1. Шаблон явной схемы

Уравнение для решения одномерного уравнения теплопроводности во внутренних точках:

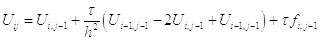 при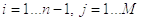

Для уменьшения количества расчетом сведем результаты в сводную таблицу.

Таблица 4

Таблица 5

Неявная схема

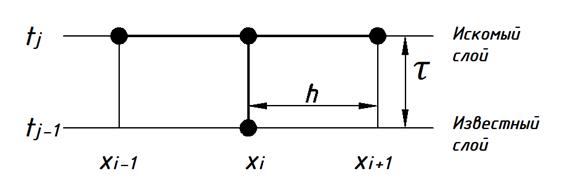
Рис. 2. Шаблон неявной схемы

Для решения одномерного уравнения теплопроводности используется система линейных алгебраических уравнений, которая решается методом прогонки.

,

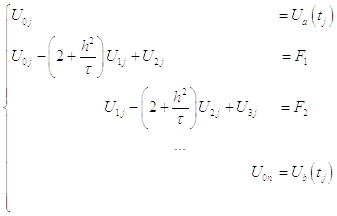где ,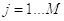

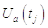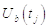 и  - краевые условия,

.

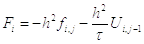Формулы для методы прогонки:

·        прямой ход

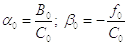
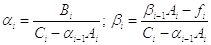
·        обратный ход .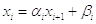

Таблица 6

1-й шаг

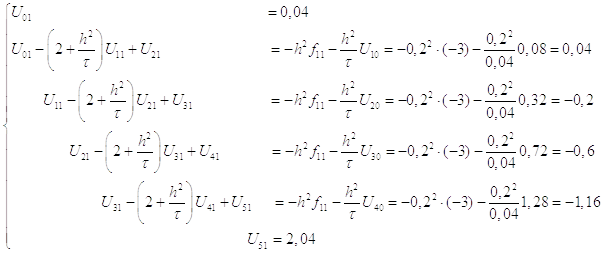
Прямой ход:

1)               

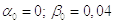
2)     

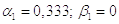
3)     

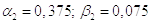
4)     

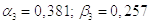
5)     

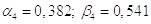
6)     

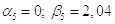
Обратный ход:

1)     

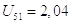
2)     

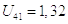
3)     

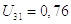
4)     

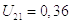
5)     

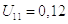
6)     

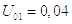
Для остальных 2-х шагов составляются аналогичные системы линейных уравнений. Результаты запишем в виде таблицы.

Таблица 7

Таблица 8

Сравнение результатов

Из представленной таблицы видно, что результаты решения одномерного уравнения теплопроводности по явной и неявной схеме полностью совпали.

Выводы

1.            Решения краевой задачи методом Ритца и методом Бубнова-Галеркина дали одинаковые результаты. Следовательно, можно сделать вывод, что оба метода являются эффективными.

2.            Решения одномерного уравнения теплопроводности по явной и неявной схеме полностью совпадают. Следовательно, можно сделать вывод, что оба метода являются эффективными.