Министерство
образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Санкт-Петербургский государственный архитектурно-строительный университет»
Кафедра прикладной математики и информатики
Дисциплина: Численные методы
КУРСОВАЯ
РАБОТА
по теме:
Численные методы решения дифференциальных уравнений
Выполнил студент
Группы ПМ-3
Бакусов П.А.
Проверил:
Вагер Б.Г.
Санкт-Петербург
2016
Оглавление
1. Дифференциальное
уравнение IV порядка
3
2. Уравнение
теплопроводности
6
2.1. Явная схема
6
2.2. Неявная схема
7
3. Волновое уравнение
9
3.1. Явная схема
9
3.2. Неявная схема
10
4. Дифференциальное
уравнение II порядка
12
4.1. Аналитическое решение
12
4.2. Метод конечных разностей
13
4.3. Метод Ритца
14
4.4. Метод Бубнова-Галёркина
16
4.5. Метод конечных элементов
17
1. Дифференциальное уравнение IV порядка
Задача: Найти решение дифференциального уравнения IV порядка:
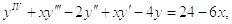
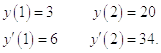
Решение:
Из общего вида уравнения:

определяем: 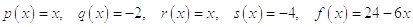 , после чего
записываем внутренние узлы разностной сетки с шагом
, после чего
записываем внутренние узлы разностной сетки с шагом 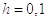 для
дифференциального уравнения и вычисляем значения коэффициентов этого уравнения
в соответствующих узлах:
для
дифференциального уравнения и вычисляем значения коэффициентов этого уравнения
в соответствующих узлах:
|
i |
xi |
pi |
qi |
ri |
si |
fi |
|
0 |
1,0 |
– |
– |
– |
– |
– |
|
1 |
1,1 |
– |
– |
– |
– |
– |
|
2 |
1,2 |
1,2 |
-2,0 |
1,2 |
-4,0 |
16,8 |
|
3 |
1,3 |
1,3 |
-2,0 |
1,3 |
-4,0 |
16,2 |
|
4 |
1,4 |
1,4 |
-2,0 |
1,4 |
-4,0 |
15,6 |
|
5 |
1,5 |
1,5 |
-2,0 |
1,5 |
-4,0 |
15,0 |
|
6 |
1,6 |
1,6 |
-2,0 |
1,6 |
-4,0 |
14,4 |
|
7 |
1,7 |
1,7 |
-2,0 |
1,7 |
-4,0 |
13,8 |
|
8 |
1,8 |
1,8 |
-2,0 |
1,8 |
-4,0 |
13,2 |
|
9 |
1,9 |
– |
– |
– |
– |
– |
|
10 |
2,0 |
– |
– |
– |
– |
– |
Вычисляем коэффициенты системы по следующим формулам:
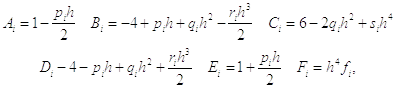
а из краевых условий получаем, что:
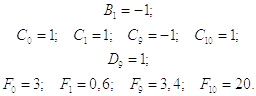
|
i |
Ai |
Bi |
Ci |
Di |
Ei |
Fi |
|
0 |
– |
– |
1,00000 |
– |
– |
3,00000 |
|
1 |
– |
-1,00000 |
1,00000 |
– |
– |
0,60000 |
|
2 |
0,94000 |
-3,90060 |
6,03960 |
-4,13940 |
1,06000 |
0,16800 |
|
3 |
0,93500 |
-3,89065 |
6,03960 |
-4,14935 |
1,06500 |
0,16200 |
|
4 |
0,93000 |
-3,88070 |
6,03960 |
-4,15930 |
1,07000 |
0,15600 |
|
5 |
0,92500 |
-3,87075 |
6,03960 |
-4,16925 |
1,07500 |
0,15000 |
|
6 |
0,92000 |
-3,86080 |
6,03960 |
-4,17920 |
1,08000 |
0,14400 |
|
7 |
0,91500 |
-3,85085 |
6,03960 |
-4,18915 |
1,08500 |
0,13800 |
|
8 |
0,91000 |
-3,84090 |
6,03960 |
-4,19910 |
1,09000 |
0,13200 |
|
9 |
– |
– |
-1,00000 |
1,00000 |
– |
3,40000 |
|
10 |
– |
– |
1,00000 |
– |
– |
20,00000 |
Конечно-разностная система уравнений заданной краевой задачи имеет вид:
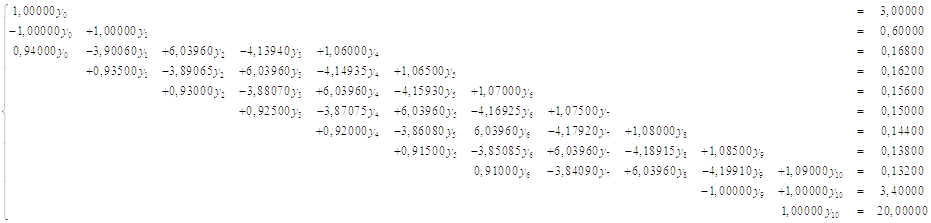
Решаем эту систему уравнений методом прогонки для пятидиагональной матрицы. Сначала вычислим коэффициенты прогонки по формулам:

|
i |
αi |
βi |
γi |
|
0 |
0,00000 |
0,00000 |
3,00000 |
|
1 |
0,00000 |
0,00000 |
3,60000 |
|
2 |
0,68537 |
-0,17550 |
1,85837 |
|
3 |
1,02771 |
-0,31573 |
1,14611 |
|
4 |
1,23280 |
-0,42072 |
0,78266 |
|
5 |
1,36927 |
-0,50055 |
0,57124 |
|
6 |
1,46655 |
-0,56278 |
0,43717 |
|
7 |
1,53937 |
-0,61246 |
0,34685 |
|
8 |
1,59594 |
-0,65297 |
0,28324 |
|
9 |
1,00000 |
0,00000 |
-3,40000 |
|
10 |
0,00000 |
0,00000 |
20,00000 |
Найденные коэффициенты подставляем в формулу:

с помощью которой находим искомые yi:
|
i |
yi |
|
0 |
3,00000 |
|
1 |
3,60000 |
|
2 |
4,31477 |
|
3 |
5,19225 |
|
4 |
6,28031 |
|
5 |
7,62721 |
|
6 |
9,28195 |
|
7 |
11,29455 |
|
8 |
13,71631 |
|
9 |
16,60000 |
|
10 |
20,00000 |
Невязка правой и левой
части близка к нулю, что говорит о корректности полученных данных.
2. Уравнение теплопроводности
Задача: Найти решение одномерного уравнения теплопроводности:
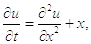
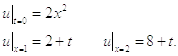
2.1. Явная схема
Решение:
Строим
сетку по x с шагом 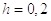 , а по t
с шагом
, а по t
с шагом 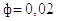 (шаг по t
мы получили из условия сходимости метода:
(шаг по t
мы получили из условия сходимости метода: 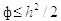 ). Вычислим значения
на нулевом слое с помощью начального условия:
). Вычислим значения
на нулевом слое с помощью начального условия:

и получим следующие значения:
|
x0=1,0 |
x1=1,2 |
x2=1,4 |
x3=1,6 |
x4=1,8 |
x5=2,0 |
|
|
t0=0,00 |
2,00000 |
2,88000 |
3,92000 |
5,12000 |
6,48000 |
8,00000 |
Теперь вычислим значения на первом слое. Для этого сначала получим значения на краях (x0 и x5) с помощью граничных условий при t1=0,02:

После чего находим значения во внутренних точках по формуле (в данном случае параметр i, параметр переменной x, меняется в пределах от 1 до 4, а параметр j, параметр переменной t, равен 1):
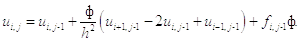
В итоге получаем значения для первого слоя:
|
x0=1,0 |
x1=1,2 |
x2=1,4 |
x3=1,6 |
x4=1,8 |
x5=2,0 |
|
|
t1=0,02 |
2,02000 |
2,98400 |
4,02800 |
5,23200 |
6,59600 |
8,02000 |
Аналогичным образом рассчитываются остальные 49 слоёв. Таблица значений первых одиннадцати слоёв представлена ниже.
|
x0=1,0 |
x1=1,2 |
x2=1,4 |
x3=1,6 |
x4=1,8 |
x5=2,0 |
|
|
t0=0,00 |
2,00000 |
2,88000 |
3,92000 |
5,12000 |
6,48000 |
8,00000 |
|
t1=0,02 |
2,02000 |
2,98400 |
4,02800 |
5,23200 |
6,59600 |
8,02000 |
|
t2=0,04 |
2,04000 |
3,04800 |
4,13600 |
5,34400 |
6,66200 |
8,04000 |
|
t3=0,06 |
2,06000 |
3,11200 |
4,22400 |
5,43100 |
6,72800 |
8,06000 |
|
t4=0,08 |
2,08000 |
3,16600 |
4,29950 |
5,50800 |
6,78150 |
8,08000 |
|
t5=0,10 |
2,10000 |
3,21375 |
4,36500 |
5,57250 |
6,83000 |
8,10000 |
|
t6=0,12 |
2,12000 |
3,25650 |
4,42112 |
5,62950 |
6,87225 |
8,12000 |
|
t7=0,14 |
2,14000 |
3,29456 |
4,47100 |
5,67868 |
6,91075 |
8,14000 |
|
t8=0,16 |
2,16000 |
3,32950 |
4,51462 |
5,72287 |
6,94534 |
8,16000 |
|
t9=0,18 |
2,18000 |
3,36131 |
4,55418 |
5,76198 |
6,97743 |
8,18000 |
|
t10=0,20 |
2,20000 |
3,39109 |
4,58964 |
5,79781 |
7,00699 |
8,20000 |
Невязка правой и левой части близка к нулю, что говорит о корректности полученных данных.
2.2. Неявная схема
Решение:
Строим
сетку по x с шагом 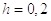 , а по t
с шагом
, а по t
с шагом  . Вычислим значения
на нулевом слое с помощью начального условия:
. Вычислим значения
на нулевом слое с помощью начального условия:

и получим следующие значения:
|
x0=1,0 |
x1=1,2 |
x2=1,4 |
x3=1,6 |
x4=1,8 |
x5=2,0 |
|
|
t0=0,00 |
2,00000 |
2,88000 |
3,92000 |
5,12000 |
6,48000 |
8,00000 |
Теперь вычислим значения на первом слое. Для этого составляется система (в данном случае параметр j, параметр переменной t, равен 1):
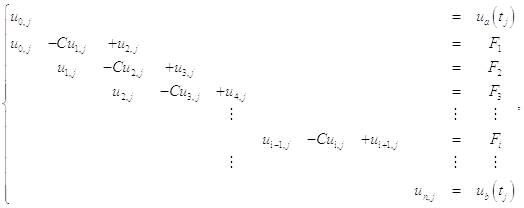
где ui,j
–
неизвестные, которые мы ищем, 
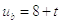 – граничные
условия, Fi
рассчитываются по формуле:
– граничные
условия, Fi
рассчитываются по формуле:
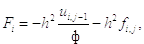
а коэффициенты C имеют вид:
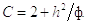
В итоге получаем значения для первого слоя:
|
x0=1,0 |
x1=1,2 |
x2=1,4 |
x3=1,6 |
x4=1,8 |
x5=2,0 |
|
|
t1=0,04 |
2,04000 |
3,02327 |
4,10181 |
5,30618 |
6,63272 |
8,04000 |
Аналогичным образом рассчитываются остальные 24 слоя. Таблица значений первых шести слоёв представлена ниже.
|
x0=1,0 |
x1=1,2 |
x2=1,4 |
x3=1,6 |
x4=1,8 |
x5=2,0 |
|
|
t0=0,00 |
2,00000 |
2,88000 |
3,92000 |
5,12000 |
6,48000 |
8,00000 |
|
t1=0,04 |
2,04000 |
3,02327 |
4,10181 |
5,30618 |
6,63272 |
8,04000 |
|
t2=0,08 |
2,08000 |
3,13335 |
4,24879 |
5,45520 |
6,74664 |
8,08000 |
|
t3=0,12 |
2,12000 |
3,22296 |
4,36753 |
5,57486 |
6,83783 |
8,12000 |
|
t4=0,16 |
2,16000 |
3,29863 |
4,46494 |
5,67265 |
6,91416 |
8,16000 |
|
t5=0,20 |
2,20000 |
3,36441 |
4,54662 |
5,75449 |
6,98022 |
8,20000 |
Невязка правой и левой части близка к нулю, что говорит о корректности полученных данных.
3. Волновое уравнение
Задача: Найти решение одномерного волнового уравнения:
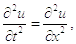
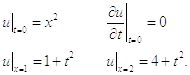
3.1. Явная схема
Решение:
Строим
сетку по x с шагом 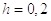 , а по t
с шагом
, а по t
с шагом 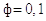 (шаг по t
мы получили из условия сходимости метода:
(шаг по t
мы получили из условия сходимости метода: 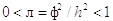 ). Вычислим значения
на нулевом и первом слое с помощью начальных условий:
). Вычислим значения
на нулевом и первом слое с помощью начальных условий:
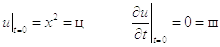
и формулы (параметр i, параметр переменной x, меняется в пределах от 0 до 6):

и получим следующие значения:
|
x0=1,0 |
x1=1,2 |
x2=1,4 |
x3=1,6 |
x4=1,8 |
x5=2,0 |
|
|
t0=0,0 |
1,00000 |
1.44000 |
1,96000 |
2,56000 |
3,24000 |
4,00000 |
|
t1=0,1 |
1.01000 |
1.45000 |
1.97000 |
2,57000 |
3,25000 |
4,01000 |
Теперь вычислим значения на втором слое. Для этого сначала получим значения на краях (x0 и x5) с помощью граничных условий при t2=0,2:
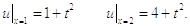
После чего находим значения во внутренних точках по формуле (в данном случае параметр i, параметр переменной x, меняется в пределах от 1 до 4, а параметр j, параметр переменной t, равен 1):
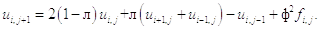
В итоге получаем значения для второго слоя:
|
x0=1,0 |
x1=1,2 |
x2=1,4 |
x3=1,6 |
x4=1,8 |
x5=2,0 |
|
|
t2=0,1 |
1.04000 |
1.48000 |
2.00000 |
2,60000 |
3,28000 |
4,04000 |
Аналогичным образом рассчитываются остальные восьми слоёв. Таблица значений всех одиннадцати слоёв представлена ниже.
|
x0=1,0 |
x1=1,2 |
x2=1,4 |
x3=1,6 |
x4=1,8 |
x5=2,0 |
|
|
t0=0,0 |
1,00000 |
1.44000 |
1,96000 |
2,56000 |
3,24000 |
4,00000 |
|
t1=0,1 |
1.01000 |
1.45000 |
1.97000 |
2,57000 |
3,25000 |
4,01000 |
|
t2=0,2 |
1.04000 |
1.48000 |
2.00000 |
2,60000 |
3,28000 |
4,04000 |
|
t3=0,3 |
1.09000 |
1.53000 |
2.05000 |
2,65000 |
3,33000 |
4,09000 |
|
t4=0,4 |
1.16000 |
1.60000 |
2.12000 |
2,72000 |
3,40000 |
4,16000 |
|
t5=0,5 |
1.25000 |
1.69000 |
2.21000 |
2,81000 |
3,49000 |
4,25000 |
|
t6=0,6 |
1.36000 |
1.80000 |
2.32000 |
2,92000 |
3,60000 |
4,36000 |
|
t7=0,7 |
1.49000 |
1.93000 |
2.45000 |
3,05000 |
3,73000 |
4,49000 |
|
t8=0,8 |
1.64000 |
2.08000 |
2.60000 |
3,20000 |
3,88000 |
4,64000 |
|
t9=0,9 |
1.81000 |
2.25000 |
2.77000 |
3,37000 |
4,05000 |
4,81000 |
|
t10=1,0 |
2,00000 |
2.44000 |
2.96000 |
3,56000 |
4,24000 |
5,00000 |
Невязка правой и левой части близка к нулю, что говорит о верности полученных данных.
3.2. Неявная схема
Решение:
Строим
сетку по x с шагом 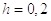 , а по t
с шагом
, а по t
с шагом 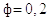 . Вычислим значения
на нулевом и первом слое с помощью начальных условий:
. Вычислим значения
на нулевом и первом слое с помощью начальных условий:
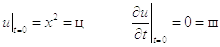
и формулы (параметр i, параметр переменной x, меняется в пределах от 0 до 6):

и получим следующие значения:
|
x0=1,0 |
x1=1,2 |
x2=1,4 |
x3=1,6 |
x4=1,8 |
x5=2,0 |
|
|
t0=0,0 |
1,00000 |
1,44000 |
1,96000 |
2,56000 |
3,24000 |
4,00000 |
|
t1=0,2 |
1.04000 |
1,48000 |
2,00000 |
2,60000 |
3,28000 |
4,04000 |
Теперь вычислим значения на втором слое. Для этого составляется система (в данном случае параметр j, параметр переменной t, равен 1):

где ui,j
–
неизвестные, которые мы ищем, 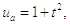
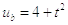 – граничные
условия, Fi
рассчитываются по формуле:
– граничные
условия, Fi
рассчитываются по формуле:
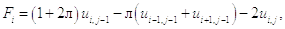
а коэффициенты C имеют вид:
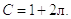
В итоге получаем значения для второго слоя:
|
x0=1,0 |
x1=1,2 |
x2=1,4 |
x3=1,6 |
x4=1,8 |
x5=2,0 |
|
|
t2=0,4 |
1.16000 |
1,60000 |
2,12000 |
2,71999 |
3,39999 |
4,16000 |
Аналогичным образом рассчитываются остальные три слоя. Таблица значений всех шести слоёв представлена ниже.
|
x0=1,0 |
x1=1,2 |
x2=1,4 |
x3=1,6 |
x4=1,8 |
x5=2,0 |
|
|
t0=0,0 |
1,00000 |
1,44000 |
1,96000 |
2,56000 |
3,24000 |
4,00000 |
|
t1=0,2 |
1.04000 |
1,48000 |
2,00000 |
2,60000 |
3,28000 |
4,04000 |
|
t2=0,4 |
1.16000 |
1,60000 |
2,12000 |
2,71999 |
3,39999 |
4,16000 |
|
t3=0,6 |
1.36000 |
1,80000 |
2,31999 |
2,91999 |
3,59999 |
4,36000 |
|
t4=0,8 |
1.64000 |
2,08000 |
2,59999 |
3,19999 |
3,87999 |
4,64000 |
|
t5=1,0 |
2.00000 |
2,44000 |
2,95999 |
3,55999 |
4,23999 |
5,00000 |
Невязка правой и левой части близка к нулю, что говорит о верности полученных данных.
4. Дифференциальное уравнение II порядка
Задача: Найти решение дифференциального уравнения II порядка:
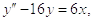

4.1. Аналитическое решение
Решение:
Решение будем искать в виде суммы общего решения однородного уравнения и частного неоднородного:
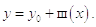
Рассмотрим однородное уравнение:
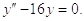
Его характеристический полином имеет вид:

корни которого: 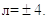
Поскольку корни вещественные, общее решение однородного уравнения будет иметь вид:
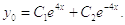
Теперь найдём частное решение неоднородного уравнения в виде:

Для этого составим систему:
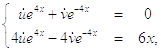
решением которой будет:

Решив эти уравнения, получаем функции u(x) и v(x):
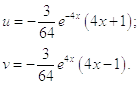
Частное решение неоднородного уравнения имеет вид:
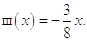
В итоге, получаем решение изначального уравнения:

Подставив граничные условия и найдя коэффициенты C1 и C2, получаем решение задачи Коши:
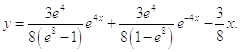
Значения функции y на интервале [0,1] представлены в таблице:
|
x |
Аналит |
|
x=0,0 |
0,00000 |
|
x=0,1 |
-0,03185 |
|
x=0,2 |
-0,06279 |
|
x=0,3 |
-0,09175 |
|
x=0,4 |
-0,11735 |
|
x=0,5 |
-0,13766 |
|
x=0,6 |
-0,14988 |
|
x=0,7 |
-0,14993 |
|
x=0,8 |
-0,13172 |
|
x=0,9 |
-0,08623 |
|
x=1,0 |
0,00000 |
4.2. Метод конечных разностей
Решение:
Из общего вида уравнения:
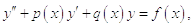
определяем: 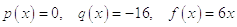 , после чего
записываем внутренние узлы разностной сетки с шагом
, после чего
записываем внутренние узлы разностной сетки с шагом 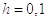 для
дифференциального уравнения и вычисляем значения коэффициентов этого уравнения
в соответствующих узлах:
для
дифференциального уравнения и вычисляем значения коэффициентов этого уравнения
в соответствующих узлах:
|
i |
xi |
pi |
qi |
Ai |
Bi |
Ci |
Fi |
αi |
βi |
|
0 |
1,00 |
– |
– |
– |
1,00 |
– |
0,00 |
0,00000 |
0,00000 |
|
1 |
1,10 |
– |
– |
1,00 |
1,16 |
1,00 |
0,60 |
0,46296 |
-0,00277 |
|
2 |
1,20 |
1,20 |
-2,00 |
1,00 |
1,16 |
1,00 |
1,20 |
0,58926 |
-0,00870 |
|
3 |
1,30 |
1,30 |
-2,00 |
1,00 |
1,16 |
1,00 |
1,80 |
0,63664 |
-0,01700 |
|
4 |
1,40 |
1,40 |
-2,00 |
1,00 |
1,16 |
1,00 |
2,40 |
0,65644 |
-0,02691 |
|
5 |
1,50 |
1,50 |
-2,00 |
1,00 |
1,16 |
1,00 |
3,00 |
0,66509 |
-0,03785 |
|
6 |
1,60 |
1,60 |
-2,00 |
1,00 |
1,16 |
1,00 |
3,60 |
0,66893 |
-0,04940 |
|
7 |
1,70 |
1,70 |
-2,00 |
1,00 |
1,16 |
1,00 |
4,20 |
0,67066 |
-0,06130 |
|
8 |
1,80 |
1,80 |
-2,00 |
1,00 |
1,16 |
1,00 |
4,80 |
0,67143 |
-0,07338 |
|
9 |
1,90 |
– |
– |
1,00 |
1,16 |
1,00 |
5,40 |
0,67178 |
-0,08557 |
|
10 |
2,00 |
– |
– |
– |
1,00 |
– |
6,00 |
0,00000 |
0,00000 |
Где коэффициенты системы рассчитываются по следующим формулам:

Аналогично дифференциальному уравнению IV порядка строится конечно-разностная система, только в данном случае с дрёхдиагональной матрицей.
Найденные коэффициенты подставляем в формулу:

с помощью которой находим искомые yi:
|
x |
Аналит |
КР |
|
x=0,0 |
0,00000 |
0,00000 |
|
x=0,1 |
-0,03185 |
-0,03174 |
|
x=0,2 |
-0,06279 |
-0,06257 |
|
x=0,3 |
-0,09175 |
-0,09140 |
|
x=0,4 |
-0,11735 |
-0,11686 |
|
x=0,5 |
-0,13766 |
-0,13702 |
|
x=0,6 |
-0,14988 |
-0,14911 |
|
x=0,7 |
-0,14993 |
-0,14905 |
|
x=0,8 |
-0,13172 |
-0,13085 |
|
x=0,9 |
-0,08623 |
-0,08557 |
|
x=1,0 |
0,00000 |
0,00000 |
4.3. Метод Ритца
Решение:
Сначала приведём дифференциальное уравнение к виду оператора Штурма-Лиувилля:
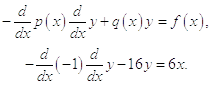
Решение будем искать в виде:
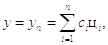
где φi – базисные функции, а ci – неизвестные коэффициенты.
Поскольку аналитическое решение – это сумма показательных функций, базис выберем показательным:
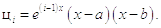
Рассмотрим функционал:
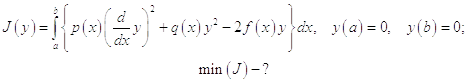
Уравнение Эйлера для него будет иметь вид изначального дифференциального уравнения, что говорит об эквивалентности задач. Поэтому мы можем воспользоваться методом Ритца, который сводит задачу на поиск минимума функционала к решению системы линейных уравнений.
Коэффициенты левой и правой части системы рассчитываются по формулам:
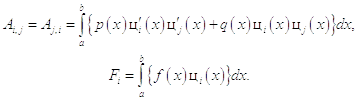
Найденные решения системы являются искомыми коэффициентами.
Прогнав метод Ритца для четырёх приближений, получаем четыре функции, значения которых на интервале [0,1] представлены в таблице:
|
x |
Аналит |
1 прибл |
2 прибл |
3 прибл |
4 прибл |
|
x=0,0 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
|
x=0,1 |
-0,03185 |
-0,05192 |
-0,02900 |
-0,03215 |
-0,03186 |
|
x=0,2 |
-0,06279 |
-0,09230 |
-0,05976 |
-0,06289 |
-0,06276 |
|
x=0,3 |
-0,09175 |
-0,12115 |
-0,09032 |
-0,09157 |
-0,09171 |
|
x=0,4 |
-0,11735 |
-0,13846 |
-0,11824 |
-0,11705 |
-0,11731 |
|
x=0,5 |
-0,13766 |
-0,14423 |
-0,14045 |
-0,13747 |
-0,13763 |
|
x=0,6 |
-0,14988 |
-0,13846 |
-0,15317 |
-0,14996 |
-0,14984 |
|
x=0,7 |
-0,14993 |
-0,12115 |
-0,15176 |
-0,15021 |
-0,14986 |
|
x=0,8 |
-0,13172 |
-0,09230 |
-0,13056 |
-0,13192 |
-0,13164 |
|
x=0,9 |
-0,08623 |
-0,05192 |
-0,08272 |
-0,08609 |
-0,08618 |
|
x=1,0 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
4.4. Метод Бубнова-Галёркина
Решение:
Решение будем искать в виде:
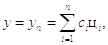
где φi – базисные функции, а ci – неизвестные коэффициенты.
Поскольку аналитическое решение – это сумма показательных функций, базис выберем показательным:
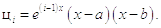
Выпишем дифференциальный оператор:
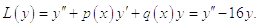
Метод Бубнова-Галёркина сводит поиск решения дифференциального уравнения к решению линейной системы уравнений вида:

Найденные решения системы являются искомыми коэффициентами.
Прогнав метод Бубнова-Галёркина для четырёх приближений, получаем четыре функции, значения которых на интервале [0,1] представлены в таблице:
|
x |
Аналит |
1 прибл |
2 прибл |
3 прибл |
4 прибл |
|
x=0,0 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
|
x=0,1 |
-0,03185 |
-0,05192 |
-0,02900 |
-0,03215 |
-0,03186 |
|
x=0,2 |
-0,06279 |
-0,09230 |
-0,05976 |
-0,06289 |
-0,06276 |
|
x=0,3 |
-0,09175 |
-0,12115 |
-0,09032 |
-0,09157 |
-0,09171 |
|
x=0,4 |
-0,11735 |
-0,13846 |
-0,11824 |
-0,11705 |
-0,11731 |
|
x=0,5 |
-0,13766 |
-0,14423 |
-0,14045 |
-0,13747 |
-0,13763 |
|
x=0,6 |
-0,14988 |
-0,13846 |
-0,15317 |
-0,14996 |
-0,14984 |
|
x=0,7 |
-0,14993 |
-0,12115 |
-0,15176 |
-0,15021 |
-0,14986 |
|
x=0,8 |
-0,13172 |
-0,09230 |
-0,13056 |
-0,13192 |
-0,13164 |
|
x=0,9 |
-0,08623 |
-0,05192 |
-0,08272 |
-0,08609 |
-0,08618 |
|
x=1,0 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
4.5. Метод конечных элементов
Решение:
Решение будем искать в виде:
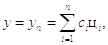
где φi – базисные функции, а ci – неизвестные коэффициенты.
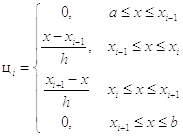
здесь h – это шаг по оси 0x.
Метод конечных элементов сводит поиск решения дифференциального уравнения к решению линейной системы уравнений вида:
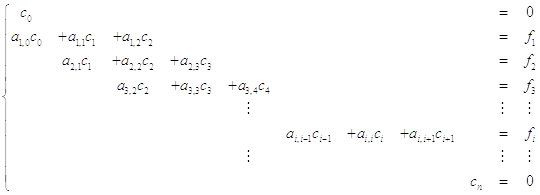
где коэффициенты левой и правой части ищутся по формулам:
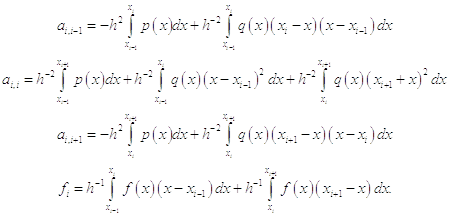
Найденные решения системы являются искомыми коэффициентами.
Значения найденной функции y на интервале [0,1] представлены в таблице:
|
x |
Аналит |
МКЭ |
|
x=0,0 |
0,00000 |
0,00000 |
|
x=0,1 |
-0,03185 |
-0,03196 |
|
x=0,2 |
-0,06279 |
-0,06302 |
|
x=0,3 |
-0,09175 |
-0,09211 |
|
x=0,4 |
-0,11735 |
-0,11785 |
|
x=0,5 |
-0,13766 |
-0,13831 |
|
x=0,6 |
-0,14988 |
-0,15067 |
|
x=0,7 |
-0,14993 |
-0,15083 |
|
x=0,8 |
-0,13172 |
-0,13262 |
|
x=0,9 |
-0,08623 |
-0,08691 |
|
x=1,0 |
0,00000 |
0,00000 |
Составив сводную таблицу полученных значений с помощью различных методов, можно сделать вывод, что наиболее точными являются методы Ритца и Бубнова-Галёркина (при 4 приближении).
|
x |
Аналит |
КР |
Ритц |
Бубнов-Галёркин |
МКЭ |
||||||
|
1 прибл |
2 прибл |
3 прибл |
4 прибл |
1 прибл |
2 прибл |
3 прибл |
4 прибл |
||||
|
x=0,0 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
|
x=0,1 |
-0,03185 |
-0,03174 |
-0,05192 |
-0,02900 |
-0,03215 |
-0,03186 |
-0,05192 |
-0,02900 |
-0,03215 |
-0,03186 |
-0,03196 |
|
x=0,2 |
-0,06279 |
-0,06257 |
-0,09230 |
-0,05976 |
-0,06289 |
-0,06276 |
-0,09230 |
-0,05976 |
-0,06289 |
-0,06276 |
-0,06302 |
|
x=0,3 |
-0,09175 |
-0,09140 |
-0,12115 |
-0,09032 |
-0,09157 |
-0,09171 |
-0,12115 |
-0,09032 |
-0,09157 |
-0,09171 |
-0,09211 |
|
x=0,4 |
-0,11735 |
-0,11686 |
-0,13846 |
-0,11824 |
-0,11705 |
-0,11731 |
-0,13846 |
-0,11824 |
-0,11705 |
-0,11731 |
-0,11785 |
|
x=0,5 |
-0,13766 |
-0,13702 |
-0,14423 |
-0,14045 |
-0,13747 |
-0,13763 |
-0,14423 |
-0,14045 |
-0,13747 |
-0,13763 |
-0,13831 |
|
x=0,6 |
-0,14988 |
-0,14911 |
-0,13846 |
-0,15317 |
-0,14996 |
-0,14984 |
-0,13846 |
-0,15317 |
-0,14996 |
-0,14984 |
-0,15067 |
|
x=0,7 |
-0,14993 |
-0,14905 |
-0,12115 |
-0,15176 |
-0,15021 |
-0,14986 |
-0,12115 |
-0,15176 |
-0,15021 |
-0,14986 |
-0,15083 |
|
x=0,8 |
-0,13172 |
-0,13085 |
-0,09230 |
-0,13056 |
-0,13192 |
-0,13164 |
-0,09230 |
-0,13056 |
-0,13192 |
-0,13164 |
-0,13262 |
|
x=0,9 |
-0,08623 |
-0,08557 |
-0,05192 |
-0,08272 |
-0,08609 |
-0,08618 |
-0,05192 |
-0,08272 |
-0,08609 |
-0,08618 |
-0,08691 |
|
x=1,0 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |














 (zip - application/zip)
(zip - application/zip)










