Биномиальный критерий — это непараметрический метод, позволяющий легко проверить, повлияла ли независимая переменная на выполнение задания испытуемыми, при этом методе сначала подсчитывают число испытуемых, у которых результаты снизились, а затем сравнивают его с тем числом, которого можно было ожидать на основе чистой случайности (в нашем случае вероятность случайного события 1:2). Далее определяют разницу между этими двумя числами, чтобы выяснить, насколько она достоверна.
Биномиальный критерий особенно часто используют при анализе данных, получаемых в исследованиях по парапсихологии. С помощью этого критерия легко можно сравнить, например, число так называемых телепатических или психокинетических реакций (X) с числом сходных реакций, которое могло быть обусловлено чистой случайностью (п/2).
При подсчетах результаты, свидетельствующие о повышении эффективности, берут со знаком плюс, а о снижении — со знаком минус; случаи отсутствия разницы не учитывают.
Расчет ведется по следующей формуле:
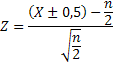
где Х — сумма «плюсов» или сумма «минусов»;
п/2 — число сдвигов в ту или в другую сторону при чистой случайности один шанс из двух. (Такая вероятность характерна, например, для п бросаний монеты. В случае же если п раз бросают игральную кость, то вероятность выпадения той или иной грани уже равна одному шансу из 6 (п/6))
0,5 — поправочный коэффициент, который добавляют к X, если X<п/2, или вычитают, если X>п/2.
Таблица Z для критических значений для уровня значимости α=0,01 и α=0,05
| Достоверные значения Z | |
| α | Z |
| 0,05 | 1,64 |
| 0,01 | 2,33 |
Пример 1. Гипотеза Н0: Под действием независимой переменной глазодвигательная координация людей после эксперимента улучшилась.
| До | 12 | 21 | 10 | 15 | 15 | 19 | 17 | 14 | 13 | 11 | 20 | 15 | 15 | 14 | 17 |
| После | 8 | 20 | 6 | 8 | 17 | 10 | 10 | 9 | 7 | 8 | 14 | 13 | 16 | 11 | 12 |
| Знак | - | - | - | - | + | - | - | - | - | - | - | - | + | - | - |
Итак, в 13 случаях результаты ухудшились, а в 2 — улучшились. Теперь нам остается вычислить Z для одного из этих двух значений X:
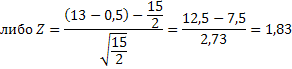
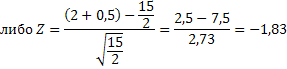
Из таблицы значений Z можно узнать, что Z для уровня значимости α=0,05 составляет 1,64. Поскольку полученная нами величина Z оказалась выше табличной, нулевую гипотезу следует отвергнуть; значит, под действием независимой переменной глазодвигательная координация действительно ухудшилась.
Пример 2. Гипотеза Н0: СОЭ в группе больных пневмонией до и после приема антибиотиков снизилось.
| До | 32 | 15 | 45 | 8 | 46 | 51 | 15 | 7 | 4 | 27 |
| После | 25 | 8 | 18 | 9 | 12 | 25 | 9 | 12 | 8 | 18 |
| Знак | - | - | - | + | - | - | - | + | + | - |
В 7 случаях результат снизился, в 3 случаях увеличился в пределах нормы.
Вычислим значения Z для «+» и «-».
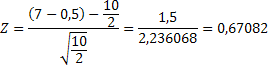
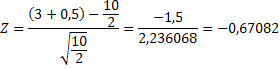
Для
уровня значимости α=0,05 и Zкр=1,64 при Zэмп Пример
3. Гипотеза Н0: Память у студентов, принимавших витамины на протяжении 1
месяца, улучшилась. Исходя
из расчетов эксперимента, у 10 из 13 студентов увеличились показатели
запоминаемости, у 2 снизились и у 1 не изменились. Вычисляя
значения Z получим: Проверим
гипотезу для уровня значимости α=0,01. Zкр=2,33, следовательно
Zэмп 1.
Годфруа Ж. Что такое психология. — М., 1992. 2. Chatillon G., 1977. Statistique
en Sciences humaines, Trois-Rivieres, Ed. SMG. 3. Gilbert N.. 1978. Statistiques, Montreal, Ed. HRW. 4. Moroney M.J., 1970. Comprendre la
statistique, Verviers,
Gerard et Cie. 5. Siegel S., 1956. Non-parametric
Statistic, New York, MacGraw-Hill Book Co.
До
25
10
2
35
60
35
20
75
50
65
45
30
50
После
45
20
35
45
15
60
40
85
50
90
35
70
70
Знак
+
+
+
+
-
+
+
+
=
+
-
+
+
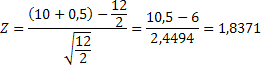
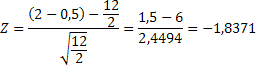
Список литературы













 (zip - application/zip)
(zip - application/zip)










