Алгоритмы эффективного статистического кодирования изображения

Минобрнауки  россии

                        Федеральное государственное автономное образовательное учреждени                 учреждение  высшего образования

                                 «Южный федеральный университет»

Кафедра: РПрУ и ТВ

Реферат

На тему: «Алгоритмы эффективного статистического кодирования изображения»

Выполнила:

Студентка группы  РТмо 1-1

Литвинова В.А.

Проверил :

д.т.н., профессор каф. РПрУ и ТВ

Мелешкин С.Н.

Таганрог 2016

Содержание:

1. Введение

2. Модель изображения

3. Структура алгоритма

4. Декорреляция изображения

    4.1. Проадаптация в кодировании изображений

    4.2. Декорреляция изображений набором предсказателей

    4.3. Адаптивная декорреляция изображений

    4.4. Межкомпонентная обработка

5. Кодирование повторяющихся последовательностей

    5.1. Кодирование участков из нулей

    5.2. Кодирование последовательностей из нулей

Заключение

Список литературы

1. Введение

Изображения, полученные от сканера, телевизионного датчика или другого сканирующего устройства, избыточны и содержат большое количество ненужной информации. Кодирование (компрессия) изображений для достижения больших коэффициентов сжатия может сопровождаться потерей некоторой части полезной информации. При кодировании без потерь сохраняются все детали изображения, в том числе и шум, но коэффициент сжатия получается на порядок меньший. Наименее востребованы алгоритмы кодирования без потерь, ввиду их малой эффективности*)Поэтому задача совершенствования неискажающих методов кодирования может показаться неактуальной и малопривлекательной. Однако, большая часть блоков алгоритма кодирования без потерь применяется в искажающих алгоритмах. Алгоритмы различаются лишь блоками, вносящими искажения. Таким образом, алгоритмы кодирования без потерь можно рассматривать как основу для искажающих алгоритмов. Без совершенных неискажающих частей нельзя построить хороший алгоритм кодирования с потерями. .

Далее будут предложены новые алгоритмы кодирования изображений без потерь и рассмотрены вопросы оптимизации отдельных частей алгоритма.

2. Модель изображения

Построение алгоритма кодирования изображений начинается с выбора способа кодирования, который в основном определяется моделью изображений. Что такое изображение? На этот вопрос есть много не похожих друг на друга ответов и, соответственно, столько же алгоритмов кодирования изображений. Одни считают, что изображение – это набор точек со случайными значениями яркости и цветности, другие, что это сумма гармоник, вейвлетов или других базисных функций. Каждая из моделей изображений имеет свои достоинства и недостатки, которые сказываются на одних типах изображений и не сказываются на других, оказываются полезными в одних приложениях и вредны в других.

Чтобы объединить полезные особенности различных моделей, дадим общее определение изображению. Рассмотрим процесс формирования изображения: это проекция трёхмерного мира на "плоскость" сетчатки глаза, фотоприёмника или другого чувствительного (и не только к свету) элемента. Множество проецируемых трёхмерных объектов даст множество деталей изображения Χ ⁿ,а условия проекции и законы природы дадут множество ℜ ⁿ правил комбинации элементов из Χ ⁿ. Сцена в кодируемом изображении создаётся с участием многих факторов различной природы. Многообразие деталей изображений и правил их композиции столь велико, что априорные предположения можно составить только об основных свойствах изображения, при этом многие закономерности останутся неучтёнными. Вдобавок ко всему, свойства изображения непостоянны в различных участках растра, что приводит к необходимости неточного (вероятностного) описания сигнала. Таким образом, модель изображения можно представить в виде некоторого вероятностного пространства

{Χ ⁿ, ℜ ⁿ, Ρ ⁿ},

где Χ ⁿ – множество значений отсчётов изображения и графических примитивов, а ℜ ⁿ  – набор правил по которым они взаимодействуют, Ρ ⁿ – семейство вероятностных мер, n – размерность множеств.

Из столь абстрактной модели изображения ничего полезного для построения алгоритма кодирования не следует, но она позволяет сравнивать различные подходы в кодировании изображений. Так некоторые алгоритмы кодируют информацию только из Χ ⁿ, используя лишь априорную информацию о статистических взаимосвязях отсчётов. Больший интерес представляют алгоритмы, кодирующие информацию как из Χ ⁿ, так и из ℜ ⁿ. Например, при использовании преобразования Карунена-Лоэва оцениваются параметры базисных функций, которые затем сохраняются вместе со сжатым изображением. Есть примеры и крайнего случая, когда кодирование осуществляется преимущественно в ℜ ⁿ. Это фрактальные алгоритмы, которые представляют изображение как набор параметров аморфных преобразований.

Множества Χ ⁿ ℜ ⁿ сильно взаимосвязаны. Пренебрегая информацией от одного множества, можно, конечно, обойтись информацией от другого, но эффективность алгоритма в этом случае будет далека от потенциальной. Информация, заключённая в изображении, многохарактерна, и для её эффективного кодирования необходимо использовать несколько моделей изображений и несколько способов компрессии, сочетая их достоинства.

3. Структура алгоритма

Известны три способа кодирования изображений: с предсказанием, с преобразованием и пирамидальное. За основу взято кодирование с предсказанием. В отличие от кодирования с преобразованием оно не вносит дополнительной избыточности и более удобно для построения адаптивных схем в отличие от пирамидального кодирования.

На рисунке 1 приведена структура алгоритма. Первый этап кодирования оценивает статистическую зависимость соседних отсчётов и устраняет корреляционную избыточность изображения. Декоррелированные отсчёты сигнала могут содержать зоны из нулей или последовательности повторяющихся нулей, которые кодируются последующими блоками. Некоторые блоки порождают дополнительные данные, чтобы повысить эффективность кодирования основного потока данных.  

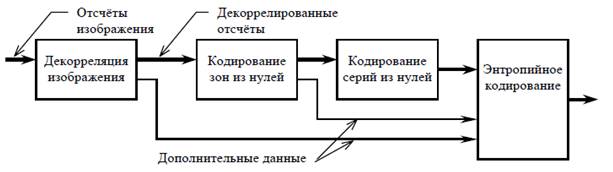
Рис. 1. Структура алгоритма кодирования изображений

Структура алгоритма не содержит каких-либо оригинальных элементов. Сегодня трудно предложить что-то, что кардинальным образом сказалось бы на эффективности кодирования. Современные алгоритмы кодирования изображений состоят из множества блоков. Применение, пусть даже замечательной, идеи в одном из блоков, часто вредит работе остальных и не даёт ощутимого эффекта. Чтобы достичь сколько-нибудь значительных результатов, необходимо оптимизировать каждый блок в отдельности и минимизировать их негативное влияние друг на друга. Незначительные выигрыши в отдельных блоках складываются в общее повышение эффективности кодирования изображений. Далее будут рассмотрены составные части алгоритма кодирования изображения, их оптимизация и взаимное влияние друг на друга.

4. Декорреляция изображения

4.1. Проадаптация в кодировании изображений

Большинство известных алгоритмов на основании "прошлых" (обработанных) отсчётов уточняют локальные свойства изображения, предполагают, что в ближайшем "будущем" свойства изображения не изменятся, и корректируют какие-то параметры кодера. При декодировании изображения на основании восстановленных отсчётов принимаются те же решения. Это классическая адаптивная схема.

В предлагаемом проадаптивном подходе для адаптации алгоритма используется продолжение сигнала. Для оценки статистических свойств кодируемого отсчёта используются как предыдущие, так и "будущие" отсчёты и даже сам кодируемый отсчёт. Несомненно, достоверность оценки возрастает, но за это приходится платить дополнительными расходами – сохранять информацию о "будущих" отсчётах или принятые решения. Проадаптивный алгоритм подстраивает свои параметры только при кодировании, а при декодировании используются значения параметров, сохранённые при кодировании. Чем больше объём дополнительных данных, тем чаще и/или точней корректируются параметры алгоритма и тем выше эффективность кодирования основного потока данных. Если корректировать параметры кодера в каждом фрагменте изображения размером W×W, то количество информации, приходящейся на отсчёт изображения, основного и дополнительного потоков данных будет зависеть от размера фрагмента изображения примерно так, как показано на рисунке 2. При некоторых условиях их сумма имеет оптимум. Экспериментальные исследования на реальных и искусственных изображениях показали, что оптимум есть всегда, но условия для его достижения существенно зависят от контекста изображения.

Рис. 2. Эффективность декорреляции

Рис. 3. Распределения ошибок предсказания

Многие адаптивные алгоритмы содержат в себе пороговые элементы и при определённых условиях применяют те или иные способы адаптации. Как правило, адаптация направлена на обнаружение резких перепадов яркости или продольных структур и предотвращение больших ошибок вблизи их. На рисунке 3 показано как изменяется форма распределения ошибок предсказания при применении адаптивных и проадаптивный методов кодирования. Адаптивные методы сокращают "хвосты" распределения, а средняя часть остаётся без изменения. Это хорошо в среднеквадратическом смысле, но слабо сказывается на энтропии данных, а, значит, и на коэффициенте сжатия. Проадаптивная схема работает как при больших, так и при малых ошибках предсказания, при этом суживается всё распределение, что более существенно снижает энтропию.

4.2. Декорреляция изображений набором предсказателей

Декорреляция изображения – первый и самый ответственный этап кодирования. Здесь не происходит собственно компрессия данных, а выполняется лишь преобразование избыточности из одной формы в другую. Большая часть избыточности заключена во взаимной зависимости отсчётов и цветовых компонент изображения. Различают зависимость линейную и нелинейную. Линейная избыточность обусловлена корреляционными связями соседних отсчётов. Линейные свойства изображения легко оцениваются по "прошлым" отсчётам и прогнозируются на "будущие". Формализовать нелинейную часть избыточности, а тем более предсказать, практически невозможно. Поэтому в процессе кодирования приходится лишь констатировать о тех или иных свойствах изображения, не вкладывающихся в корреляционную модель. На рисунке 4 приведена схема алгоритма с набором предсказателей, рассчитанных на различные текстуры изображения в районе кодируемого отсчёта: плоские, наклонные участки, перепады яркости в различных направлениях. Приведённая схема является развитием опубликованной ранее [1].

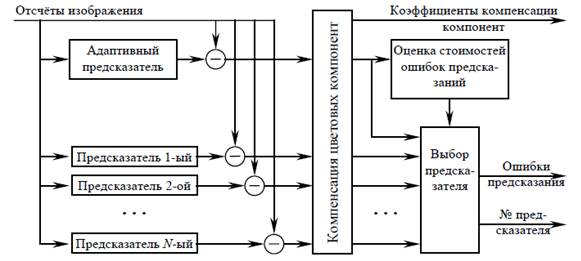
Рис. 4. Структура декоррелятора

Алгоритм декоррелирует изображение различными способами и выбирает наиболее удачный. Следует заметить, что термин "декорреляция" здесь не совсем уместен, т.к. в изображении компенсируются не только линейные взаимосвязи. Информация о нелинейных свойствах изображения сохраняется в виде номеров наиболее удачных предсказателей.

Арифметические операции в декорреляторе выполняются не на бесконечной числовой оси, а в замкнутом множестве чисел с использованием модулярной арифметики. Этот, скорее, технический приём предотвращает увеличение разрядности чисел и даёт незначительное повышение эффективности. Более подробно применение модулярной арифметики описано в [2].

Один предсказатель выбирается для группы отсчётов во фрагменте изображения размером W×W. В отдельных фрагментах изображения оптимальными будут различные значения W. Оптимальные состав и количество предсказателей также будут зависеть от локальных свойств изображения. Разделить изображение на неперекрывающиеся фрагменты различного размера очень сложно. Поэтому предлагается следующий компромиссный вариант: изображение делится на равные зоны размером W₂×W₂, которые делятся на более мелкие зоны размером W₁×W₁, которые, в свою очередь, делятся на ещё более мелкие фрагменты размером W₀×W₀. В этой структуре переменны только количество зон W₀×W₀ и их размеры.

Увеличение числа предсказателей предоставляет большие возможности выбора, но сдерживается возрастающей разрядностью номеров. В тоже время, в отдельно взятых участках изображения и не требуется большого многообразия предсказателей. Свойства изображения меняются медленно или, что точнее, постоянны в пределах ка-кого-то региона. Поэтому большинство предсказателей, оказавшихся лучшими в одном фрагменте изображения, скорее всего, будут лучшими и в соседних фрагментах. Для каждой зоны W₂×W₂ формируется множество ℵ₂ из n₂ предсказателей из N возможных. Из полученного множества формируется подмножество ℵ₁ ⊆ℵ₂ из n₁ ≤ n₂ предсказателей для каждой зоны W₁×W₁. Наконец, из полученного подмножества выбирается по одному предсказателю для каждой зоны W₀×W₀. Множества ℵ₁ и ℵ₂ могут состоять как из одного, так и из N предсказателей, т.е. 1 ≤ n₁ ≤ n₂≤ N. Такое пирамидальное кодирование номеров требует значительно меньшее количество бит, чем при прямой адресации среди N предсказателей. Возможность варьировать размеры множеств ℵ₁ и ℵ₂ позволяет регулировать степень применения предлагаемого алгоритма кодирования. Так на одних участках изображения будет применяться кодирование множеством предсказателей, а на других – одним предсказателем (n₁= n₂= 1). В последнем случае объём дополнительных данных будет незначителен, и алгоритм будет временно работать как обычный ДИКМ-кодер.

Чтобы сформировать подмножества предсказателей, необходима функция цели, позволяющая сравнивать различные варианты решений. Функция цели представляет собой сумму количеств информации основного и дополнительного потока данных и имеет вид:

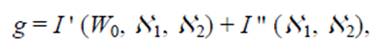                     (1)

где I " – количество информации в ошибках предсказания зоны W₂×W₂, I " – количество бит, требуемых для описания множеств ℵ₁ и ℵ₂.

Если подсчёт количества бит в дополнительном потоке данных не составит труда, то информационная ёмкость ошибок предсказаний станет известна только после де-корреляции всего изображения, когда станет известно распределение значений ошибок предсказания.

Адаптивный предсказатель, который будет описан ниже, чаще других оказывается наиболее точным. Поэтому перед декорреляцией набором предсказателей всё изображение обрабатывается одним адаптивным предсказателем. По результатам работы адаптивного предсказателя оценивается будущее распределение вероятностей значений ошибок всего алгоритма. На основании полученного распределения вычисляется количество информации, содержащееся в каждом значении ошибки, которое в дальнейшем будет использоваться в качестве стоимости ошибки при вычислении функции цели (1).

Целевая функция не дифференцируема, поэтому аналитически не минимизируется. Перебор вариантов тоже не приемлем из-за большого числа комбинаций. Неточное решение этой задачи достигается итерационным алгоритмом, известного в теории математического программирования как симплекс-метод.

4.3. Адаптивная декорреляция изображений

Адаптивный предсказатель использует линейную взаимную зависимость (корреляцию) соседних отсчётов изображения. На рисунке 5 показано расположение соседей относительно кодируемого отсчёта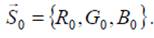

Рис. 5. Соседи кодируемого отсчёта

Оценка компонент вектора 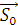 находится как линейная комбинация соответствующих компонент соседних отсчётов

R₀  = a₁*R₁₊a₂*R₂+a₃*R₃+a₄*R₄

где a₁, a₂, a₃, a₄, – весовые коэффициенты. Аналогично предсказываются компоненты G и B. Раздельное предсказание компонент вектора 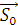 не учитывает зависимость между компонентами. Если предположить, что цветовые компоненты изображения в основном линейно зависимы, то и компенсироваться они должны также линейным оператором. Все операции по компенсации пространственной и межкомпонентной корреляций линейны, а, значит, могут быть выполнены последовательно. Эксперименты показали, что покомпонентная и последовательная обработка сигнала почти столь же эффективна, как и векторная.

Задавшись критерием минимума среднеквадратической ошибки предсказания, можно получить выражение для расчёта оптимальных в среднеквадратическом смысле коэффициентов a₁, a₂, a₃, a₄. Так для красной компоненты оно будет иметь вид:

   ₍₂₎

где < R_{i *} R_j > означает среднее произведений значений соседних отсчётов красной компоненты изображения. Аналогичные уравнения можно записать и для остальных компонент.

Следует заметить, что среднеквадратический критерий не лучшим образом подходит для оптимизации этой части алгоритма компрессии. Ничем нельзя обосновать квадратичную функцию стоимости ошибок предсказания. Очевидно, что следует минимизировать энтропию декоррелированного сигнала, но применение такого критерия не имеет решения. Попытки использовать другие компромиссные варианты функции стоимости пока не привели к успеху. Полученные решения не выражаются в таких простых статистиках, как в уравнении (2). До тех пор, пока не найден альтернативный готовый к применению критерий оптимизации, ничего не остаётся, как пользоваться средним квадратом.

Корреляции соседних отсчётов < R_{i *} R_j > , < G_{i *} G_j > , < B_{i *} B_j > не постоянны. Усреднение для их оценки должно выполняться не по всему изображению, а в локальных зонах. Размер локальной зоны, с одной стороны, должен быть меньше, чтобы уменьшить влияние нестационарности сигнала, а с другой стороны, должен быть больше, чтобы увеличить объём усредняемой выборки и повысить точность оценки. Усреднение произведений отсчётов должно быть взвешенным, т.е. влияние соседей на оценку должно иметь обратную зависимость от расстояния до кодируемого отсчёта. В предлагаемом алгоритме это достигается путём разделения изображения на вертикальные полосы и оценкой взаимных корреляций усредняющими звеньями, схема которых приведена на рисунке 6.

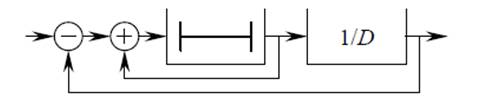
Рис. 6. Усредняющее звено

Ширина полосы и параметр усреднения D подбираются экспериментально.

4.4. Межкомпонентная обработка

Ошибки предсказаний в цветовых компонентах сильно взаимосвязаны. Если предсказатель ошибается в одной компоненте, то, скорее всего, он в той же степени ошибётся и в других компонентах. Большие ошибки возникают на краях деталей, где изменяют свои значения все цветовые компоненты изображения.

При компенсации межкомпонентной избыточности одна из компонент должна остаться без изменения. Назовём её опорной и обозначим как C₀. На основе опорной компенсируется компонента C₁. Затем уже на основе двух компонент компенсируется оставшаяся C₂

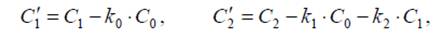
где C₀, C₁, C₂ – ошибки предсказания цветовых компонент до компенсации, а C"₁, C"₂ – после. Минимумы средних квадратов C"₁, C"₂ достигаются при следующих k₀, k₁, k₂

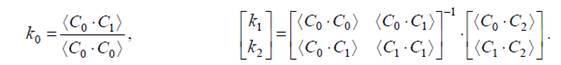
Как показали эксперименты, опорной должна быть компонента с большей, чем у других энтропией. Компонента C₁ должна иметь минимальную энтропию. Трудно объяснить, чем вызван такой порядок компенсации, однако нарушение этого порядка снижает эффективность кодирования на ~0,5%.

Произведение компонент можно усреднять по "прошлым" отсчётам (адаптивный вариант) или внутри некоторой окрестности вокруг кодируемого отсчёта (проадаптивный вариант). Последний вариант оказался более выигрышным, несмотря на дополни-тельные затраты на сохранение значений k₀, k₁, k₂.

5. Кодирование повторяющихся последовательностей

Декорреляция изображения устраняет зависимость между ближайшими соседя-ми, а более далёкие пространственные связи остаются. Большинство из этих связей несёт значительное количество информации и, в силу своей пространственной рассредоточенности, не поддаётся компактному описанию. Хорошо сжимаются только повторения значений сигнала. После декорреляции в изображении достаточно часто повторяются только нули. Выделим основные виды повторений в декоррелированном изображении:

1) Линии из нулей в горизонтальном и вертикальном направлении. Повторения в других направлениях сложно формализуются и поэтому не рассматриваются.

2) Квадратные области из нулей. Описание других форм требует дополнительных расходов, что, как правило, не оправдывается.

3) Одновременное появление нулей во всех цветовых компонентах.

Предлагаемые алгоритмы кодирования повторений применяются только в тех фрагментах изображения, где это действительно выгодно. Для этого оцениваются затраты на кодирование повторений, негативное влияние на последующие блоки и выгода от кодирования. При положительном результате сравнения обнаруженные повторения вырезаются из сигнала. При таком подходе эффект от применения алгоритмов не может быть отрицательным, как по всему изображению, так и в отдельных фрагментах.

5.1. Кодирование участков из нулей

Как видно из рисунка 1, в первую очередь выполняется кодирование зон из нулей, пока не разрушена двумерная структура изображения. Группы из нулей соответствуют участкам изображения, содержащим одноцветные детали или фон. По этой причине велика вероятность появления нулей сразу во всех цветовых компонентах.

Целью алгоритма является создание карты, обозначающие отсчёты изображения с нулевыми компонентами. На первом этапе создаётся истинная карта нулей. В последствии от части нулей придётся отказаться, т.к. точное кодирование карты нулей требует больших затрат. Следует помнить, что ноль – это самый частый символ и содержит минимальное количество информации. При формировании истинной карты нулей подсчитывается количество нулей и из соотношения с общим числом отсчётов оценивается количество информации в нуле

где n– количество нулей, M и N – размеры изображения, m – предполагаемое количество удаляемых нулей.

На втором этапе кодируются линии из нулей в вертикальном и горизонтальном направлениях. Кодирование выполняется в виде последовательного списка смещений до начал линий, их направлений и длин. Кодируются достаточно длинные линии, чтобы затраты на описание линии были заведомо оправданы.

На третьем этапе выполняется пирамидальное кодирование нулевых зон. Карта нулей представляет собой первый уровень пирамиды и содержит признаки нулевых и ненулевых отсчётов. Второй уровень имеет размеры M/2 а N/2 и каждый элемент его соответствует квадрату 2 на 2 элементов первого уровня, как это показано на рисунке 7.

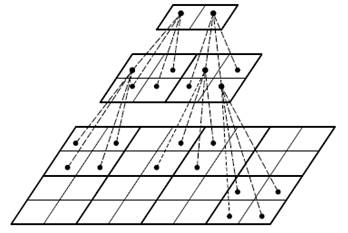
Рис. 7. Пирамидальное кодирование зон из нулей

В элементах первого и последующих уровней содержатся выигрыши в битах, которые будут получены при кодировании соответствующего участка. Значения выигрышей второго уровня складываются из стоимостей вырезаемых из сигнала нулей за вычетом 4 бит накладных расходов. Выигрыши последующих уровней складываются из выигрышей предыдущих и, также, за вычетом 4 бит накладных расходов. На верши-не пирамиды получится суммарный выигрыш или проигрыш от всего кодирования. Если кодирование зон из нулей выгодно, то пирамида просматривается в обратном порядке и строится граф, описывающий выгодную часть пирамиды. До некоторых нулей первого уровня ветви графа не дойдут. Это означает, что на их описание требуются слишком большие затраты. Алгоритм вырежет не только повторяющиеся, но и отдельно стоящие нули, если это будет выгодно.

На четвёртом этапе происходит удаление части нулей из сигнала. При этом двумерная структура изображения разрушается и в дальнейшем выполняется обработка уже одномерного сигнала.

5.2. Кодирование последовательностей из нулей

Известен алгоритм кодирования повторяющихся последовательностей – RLE (Run Length Encoding), который заключается в следующем: повторяющиеся и неповторяющиеся символы заменяются на пары, состоящие из символа и счётчика повторений. Например, последовательность AAABCC будет заменена на A3B1C2. Из приведённого примера видно, что в результате RLE-кодирования количество символов может и увеличиться.

Будем применять RLE-кодирование только к нулям, а остальные символы оставлять без изменения. Здесь возможны два варианта кодирования. В первом варианте ноль используется в качестве признака начала последовательности, за которым следует счётчик повторений. При этом одиночные нули будут расширяться в пары символов, а кодирование будет целесообразно в случае достаточного количества более длинных последовательностей.

Более предпочтительна другая схема RLE, в которой исходный алфавит кодируемой последовательности дополняется новыми символами, обозначающими группы нулей. В этом случае применение RLE-кодирования всегда уменьшает длину, если встретилась хотя бы одна пара нулей.

Может показаться, что уменьшение длины кодируемой последовательности всегда оправдывает применение RLE-кодирования. Это не так. Рассмотрим, к чему приводит замена k групп по m нулей в последовательности длиной N, содержащей n₀ нулей.

До замены количество информации в каждом нуле составляло

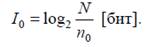
После замены длина кодируемой последовательности уменьшится на k*(m-1) бит.

Количество информации в символе, обозначающем группу, составит

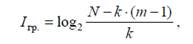
а количество информации в оставшихся нулях возрастёт до

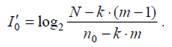
Таким образом, замена целесообразна, если справедливо неравенство

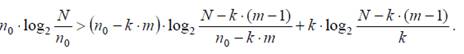
Решение неравенства даёт минимальную длину группы m, начиная с которой целесообразно применять RLE-кодирование. В неравенстве не учтено некоторое уменьшение количества информации в ненулевых символах, вследствие повышения их доли в общем потоке данных. Обычно это уменьшение незначительно и не сказывается на результатах энтропийного кодирования.

Следует заметить, что нет необходимости вводить новые символы для всех длин групп нулей. Группы могут быть разбиты на подгруппы с совпадающими длинами. В этой связи возникает задача формирования такого набора подгрупп, обеспечивающего минимальное количество информации в кодированных данных.

Рассмотрим два крайних случая. Первый, когда для каждой группы выделяется отдельный символ, т.е. возможные длины групп нулей представляют собой натуральный ряд. В этом случае сокращение длины кодируемой последовательности максимально, но и расширение алфавита также максимально. Второй, когда группы делятся на подгруппы, а длины подгрупп представляют собой показательный ряд степеней 2. В этом случае минимальны как расширение алфавита, так и сокращение длины последовательности. Компромиссным вариантом может стать ряд Фибоначчи, очередной член которого вычисляется как сумма двух предыдущих. Чтобы сделать выбор более богатым, предлагается использовать обобщённые ряды Фибоначчи [3], рассчитываемые по следующей рекуррентной формуле

a_i = a_i-1+ a _i-1-p-, где p – порядок ряда.

При p = 0 получаем, упомянутый ранее, показательный ряд; при p = 1 получится ряд Фибоначчи, а при больших p будем приближаться к натуральному ряду. В таблице 1 приведены примеры рядов различных порядков.

Выбор первого члена ряда выполняется на основании, приведённого выше неравенства, а порядок ряда – перебором, что нетрудно сделать, имея статистику по группам нулей.

В таблице 2 приведены результаты применения различных вариантов RLE-кодирования к тестовому изображению. В первом столбце приводятся длины декоррелированных компонент на входе RLE-кодера, во втором – на выходе. В скобках указаны произведения энтропии компонент (в байтах) на их длину, т.е. потенциальная эффективность энтропийного кодера. В третьем столбце приведены реальные длины последовательностей после энтропийного кодирования.

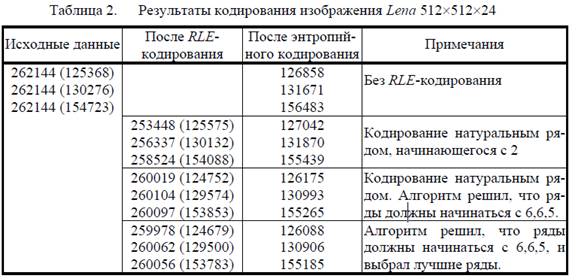
Из таблицы 2 видно, что применение известного алгоритма RLE-кодирования может вредить последующему энтропийному кодированию, несмотря на уменьшение длины кодируемой последовательности. Предлагаемый алгоритм более взвешенно подходит к кодированию повторяющихся последовательностей – кодирует не все повторения, а только достаточно выгодные. В результате достигается некий компромисс между желанием большего сокращения длины последовательности и нанесением меньшего вреда энтропийному кодеру. Эксперименты показали, что эффективность предложенного алгоритма на 2 - 7 % выше известного RLE-кодирования.

Заключение

Предлагаемый алгоритм кодирования изображений формирует два потока дан-ных: основной и дополнительный. В терминах принятой в разделе 2 модели изображения, основной поток содержит информацию из множества значений отсчётов изображения Χ ⁿ, а в дополнительном потоке содержится информация о локальных свойствах изображения из множества ℜ ⁿ. В процессе кодирования алгоритм оценивает эффект от дополнительного описания множества ℜ ⁿ и находит наилучшее отношение количеств информации от множеств Χ ⁿ ℜ ⁿ, используя при этом проадаптацию к контексту изображения.

Предложенный метод кодирования изображений набором предсказателей позволяет объединить многие известные алгоритмы в один и достичь большей эффективности, чем это достигалось по отдельности.

В статье представлена одна из первых попыток реализации нового подхода в построении алгоритмов кодирования изображений. Усилия по дальнейшему развитию алгоритмов кодирования могут быть направлены на формирование новых критериев качества работы отдельных блоков, оптимизацию существующих и синтез новых алгоритмов, отвечающих этим критериям.

Список литературы

1. Ульянов В.Н. Алгоритм кодирования изображений без потерь со множеством пред-сказателей. – Труды V межд. научно-техн. конференции "Радиолокация, навигация, связь", Воронеж, 1999, т. 1, с. 408–412.

2. Ульянов В.Н. Кодирование изображений в технических приложениях. – Томск, 1995, – 21 с. – Томск. гос. академия систем упр. и радиоэлектроники. Деп. в ВИНИТИ 6.06.95 № 1662–В95.

3. Ульянов В.Н. Кодирование повторяющихся последовательностей. – Материалы 4-ой международной конференции "Распознавание-99", Курск, 1999, с. 36–38.