Министерство образования Республики Беларусь
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ПРИКЛАДНОЙ МАТЕМАТИКИ И ИНФОРМАТИКИ
Кафедра теории вероятностей и математической статистики
РУТЬКОВ
Богдан Анатольевич
АНАЛИЗ ЭФФЕКТИВНОСТИ ПОСЛЕДОВАТЕЛЬНОГО КРИТЕРИЯ, ИСПОЛЬЗУЮЩЕГО УСРЕДНЕНИЕ НАБЛЮДЕНИЙ
Курсовая работа
Научный руководитель:
кандидат физ.-мат. наук
доцент А.Ю. Харин
Допущен к защите
«____» ___________ 2015 г.
Заведующий кафедрой
теории вероятностей и математической статистики
доктор физ.-мат. наук, профессор
Н.Н. Труш
Минск, 2015
Белорусский государственный университет
Факультет_________________________________________________________
Кафедра___________________________________________________________
ЗАДАНИЕ НА КУРСОВУЮРАБОТУ
Студент___________________________________________________________
1.
Тема ________________________________________________________________________________
_________________________________________________________________________________
_____________________________________
2 Срок представления курсовой работы к защите____________________________________________________________
3 Исходные данные для проектирования_____________________________________________________
4 Содержание курсовой работы
4.1________________________________________________________________
4. 2 _______________________________________________________________
4. 3 _______________________________________________________________
Руководитель курсовой работы___________________________________________________________
подпись, дата инициалы, фамилия
Задание принял к исполнению________________________________________________________
подпись, дата
Примечание:
Допускается дополнять или исключать пункты в бланке задания.
АННОТАЦИЯ
Рутьков Б.А. Анализ эффективности последовательного критерия, использующего усреднение наблюдений.: Курсовая работа / Минск: БГУ, 2015. – 26с.
Изучается последовательный критерий отношения вероятностей.
АННАТАЦЫЯ
Руцькоў Б.А. Аналіз эфектыўнасці паслядоўнага крытэрыю, які выкарыстоўвае асерадненне назіранняў.: Курсавы праект / Мінск: БДУ, 2015. – 26с.
Вывучаецца паслядоўны крытэрый адносіны верагоднасцяў.
ANNOTATION
Rutkov B. An analysis of the effectiveness of sequential test using averaging observations.: Term Project / Minsk: BSU, 2015. – 26p.
Studied sequential probability ratio test.
РЕФЕРАТ
Курсовая работа, 26 с., 4 источник.
Ключевые слова: ПОСЛЕДОВАТЕЛЬНЫЙ КРИТЕРИЙ, ТЕСТ ВАЛЬДА, СЛУЧАЙНАЯ ВЕЛИЧИНА, ТРЕНД, ПАРАМЕТР ЗАПРЕТА
Объект исследования – методы осуществления теста Вальда.
Цель работы – исследование устойчивости последовательных статистических тестов.
Методы исследования – написание алгоритма теста Вальда с применением методов усреднения наблюдений.
Результатом является программная реализация последовательного критерия
отношений вероятностей для проверки просто гипотезы  против единственной конкурирующей гипотезы
против единственной конкурирующей гипотезы  .
.
Областью применения является программное вычисление ошибок первого и второго родов.
ОГЛАВЛЕНИЕ
1 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 7
2 РАСПРЕДЕЛЕНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН.. 7
2.1 Равномерно распределённые случайные числа на интервале [0, 1) 7
2.2 Моделирование случайных величин с заданным законом распределения 8
2.2.1... Моделирование случайных величин с нормальным законом распределения 9
2.2.2... Генерация случайной величины с нормальным распределением по центральной предельной теореме. 9
2.2.3... Моделирование случайных величин с экспоненциальным (показательным) законом распределения. 11
3 ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ 13
3.1 Необходимость последовательного анализа. 13
3.2 Математическая модель последовательного анализа Вальда. 13
3.2.1... Основные
соотношения между 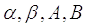 ................ 16
................ 16
3.3 Краткое обобщённое изложения теста Вальда. 17
4 РЕЗУЛЬТАТЫ И ВЫВОД 20
4.1 Модификация теста и начальные значения. 20
4.1.1... РЕЗУЛЬТАТЫ ТЕСТА ВАЛЬДА.. 21
5 ИСТОЧНИКИ 23
ПРИЛОЖЕНИЕ 24
ВВЕДЕНИЕ
Последовательный статистический критерий — последовательная статистическая процедура, используемая для проверки статистических гипотез в последовательном анализе.
Статистический последовательный анализ — раздел математической статистики, изучающий статистические методы, основанные на последовательной выборке, формируемой в ходе статистического эксперимента. Наблюдения производятся по одному (или, более общим образом, группами) и анализируются в ходе самого эксперимента с тем, чтобы на каждом этапе решить, требуются ли ещё наблюдения (решение о продолжении эксперимента) или наблюдений уже достаточно (решение об остановке эксперимента). Когда эксперимент остановлен, заключительное статистическое решение принимается на основе всех наблюденных в эксперименте данных.
Последовательный анализ Вальда(тест Вальда) – последовательное различие двух простых гипотез. Был предложен Абрахамом Вальдом в 1955 году для выборок равного объема, а затем распространен на случай выборок разных объемов.
В курсовом проекте рассматривается последовательный анализ Вальда, его реализация и результаты. На основе изученной информации некоторые методы были реализованы программно.
1 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Случайная величина – это величина, значение которой зависит от элементарного события ω. Таким образом, случайная величина – это функция, определенная на пространстве элементарных событий Ω.
Примеры случайных величин: количество отметин на верхней грани брошенной игральной кости, количество «решек» при независимом бросании монеты и т.д..
Определение случайной величины Χ как функции от элементарного события ω, т.е. функции  , отображающей пространство элементарных
событий Ω в некоторое множество Н. Мы наблюдаем всего лишь реализацию случайной величины: её
значение, соответствующее именно данному элементарному событию,
которое осуществилось в данной ситуации. А функция от элементарного события –
это теоретическое понятие, основа вероятностной модели реального явления или
процесса.
, отображающей пространство элементарных
событий Ω в некоторое множество Н. Мы наблюдаем всего лишь реализацию случайной величины: её
значение, соответствующее именно данному элементарному событию,
которое осуществилось в данной ситуации. А функция от элементарного события –
это теоретическое понятие, основа вероятностной модели реального явления или
процесса.
Если каждому
элементарному событию поставить в соответствие число 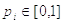 ,
для которого выполняется условие:
,
для которого выполняется условие:
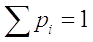
то считается, что
заданы вероятности элементарных
событий 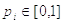 ,.
Вероятность событий в счётном пространстве (важно! так как сумма будет не
определена) элементарных событий определяется, как сумма вероятностей
элементарных событий, принадлежащих данному событию. Вероятность события, как
счётного множества пространства
элементарных событий, определяется как сумма вероятностей тех элементарных
событий, которые принадлежат этому событию.
,.
Вероятность событий в счётном пространстве (важно! так как сумма будет не
определена) элементарных событий определяется, как сумма вероятностей
элементарных событий, принадлежащих данному событию. Вероятность события, как
счётного множества пространства
элементарных событий, определяется как сумма вероятностей тех элементарных
событий, которые принадлежат этому событию.
Исходным
материалом для формирования случайных величин с различными законами
распределения служат равномерно распределённые случайные числа на интервале  , которые
используются для генерации случайных чисел любого типа распределения.
, которые
используются для генерации случайных чисел любого типа распределения.
Если обратиться к ЭВМ, то в программном обеспечении используются специальные программы – датчики случайных чисел. Обращение к этим, так называемым, датчикам случайных чисел приводит к выдаче значения от 0 до 0.999(9). Такую программу назовём RAND.
С точки зрения практики, встречаются случайные величины, о которых заранее известно, что они могут принимать, грубо говоря, любое значение в строго определённых границах, причём в этих самых границах все значения этих случайных величин имеют одинаковую вероятность.
Пример:
Предположим, что часы “стали” в какую-либо минуту и в какой-либо час(т.е.минутная стрелка остановилась на каком-либо делении). Минутная стрелка будет с одинаковой вероятностью показывать время, прошедшее от начала данного часа до остановки. Так как это время не выходит за границы одного часа, то оно является случайной величиной, принимающей с одинаковой плотностью вероятности значения.
В общем говоря, равномерно означает, что при генерации числа от 0 до 1, вероятность любого числа одинакова.
Иначе говоря, если  ,
то случайная величина
,
то случайная величина 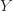 имеет непрерывное равномерное
вероятностное распределение на интервале
имеет непрерывное равномерное
вероятностное распределение на интервале  , если
фунция плотности
, если
фунция плотности  выглядит
вот так:
выглядит
вот так:
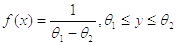
Совокупность  независимых
равномерно распределенных на отрезке
независимых
равномерно распределенных на отрезке
 случайных
величин называется последовательностью базовых случайных
случайных
величин называется последовательностью базовых случайных
чисел.
2.2 Моделирование случайных величин с заданным законом распределенияСлучайная величина характеризуется различными законами распределения.
Выше мы рассмотрели генерацию равномерно распределённых случайных чисел. Генерация случайных чисел, подчиняющихся другим законам, основана на базовой модели генерации в ЭВМ равномерно распределенных случайных чисел и последующего преобразования этих чисел. Известны несколько методов преобразования.
Существуют различные приемы преобразования случайных чисел с равномерным распределением в случайные величины с заданным законом распределения. Так, например, в качестве нормально распределенных случайных чисел можно использовать сумму нескольких независимых случайных чисел с равномерным распределением (приближение основано на центральной предельной теореме теории вероятностей, в силу которой сумма независимых случайных величин при весьма общих условиях имеет асимптотически нормальное распределение).
Рассмотрим общие приемы получения случайных чисел с заданным законом распределения из равномерно распределенных случайных чисел.
2.2.1 Моделирование случайных величин с нормальным законом распределенияНормальное (гауссово) распределение одно из самых используемых видов непрерывных распределений.
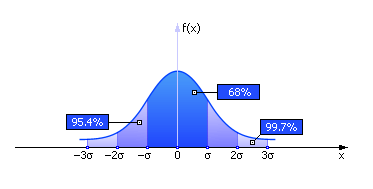
На рисунке приведён графический вид нормального закона
распределения случайной величины 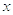 с параметрами
с параметрами
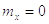 и
и 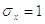 .
.
Плотность вероятностей нормального распределения определяется формулой:
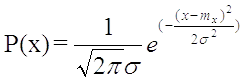
где 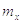 – математическое
ожидание, а
– математическое
ожидание, а  -
среднеквадратическое отклонение.
-
среднеквадратическое отклонение.
Чтобы сгенерировать случайное число с нормальным распределением вероятностей, мы воспользуемся центральной предельной теоремой.
Центральная предельная
теорема говорит о том, что сумма  одинаково
распределенных независимых случайных величин
одинаково
распределенных независимых случайных величин 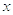 со средним
со средним 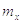 и дисперсией
и дисперсией 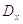 стремится к
нормально распределенной величине с параметрами
стремится к
нормально распределенной величине с параметрами 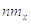 и
и  при бесконечном
увеличении
при бесконечном
увеличении  .
.
Следствием теоремы
является, в частности, и то, что для получения нормальной выборки, можно
воспользоваться базовыми случайными числами  .
.
Идея алгоритма состоит в
следующем. Определим новую случайную величину s в виде суммы базовых чисел 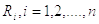 :
:
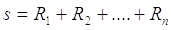
Тогда, согласно
утверждению центральной предельной теоремы, случайная величина  является
асимптотически нормальной величиной с математическим ожиданием
является
асимптотически нормальной величиной с математическим ожиданием  и дисперсией
и дисперсией  равными
соответственно:
равными
соответственно:
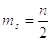
и
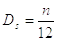
Для практического
использования формула определения случайной величины  неудобна, поэтому
введем вспомогательную случайную величину
неудобна, поэтому
введем вспомогательную случайную величину 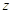 равную
равную
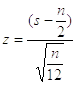
Тогда для любого нормального
распределения со средним m и дисперсией 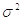 случайное
отклонение
случайное
отклонение 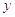 ,
соответствующее указанным выше
,
соответствующее указанным выше  случайным
числам, получается из формулы:
случайным
числам, получается из формулы:

Следовательно

Согласно той же
предельной теореме, нормальность достигается быстро даже при сравнительно
небольших значениях  .
С ростом
.
С ростом  стремится
к нормальному с параметрами
стремится
к нормальному с параметрами 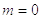 и
и
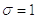 . Особенно
упрощается формула, если
. Особенно
упрощается формула, если  взять
равной 12 (т.к. мы как бы “гасим” дисперсию).
взять
равной 12 (т.к. мы как бы “гасим” дисперсию).
При этом последняя формула упрощается и принимает вид:
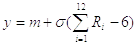
Этой формулой и задаётся
алгоритм моделирования нормальных случайных чисел с требуемыми параметрами 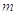 и
и  .
.
Будем брать 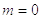 и
и 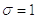 , т.е. будем
использовать нормализованный закон нормального распределения.
, т.е. будем
использовать нормализованный закон нормального распределения.
Показательным законом описываются многие физические процессы: случайное время безотказной работы электронных и ряд других изделий, случайные моменты времени поступления заказов на предприятия, службы быта, вывозов на телефонные станции, поступления судов в отдельные порты, времена поиска неисправностей в аппаратуре и т.д.
Чтобы сгенерировать случайную величину 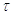 по показательному
закону, воспользуемся методом инверсии:
по показательному
закону, воспользуемся методом инверсии:
Как известно, случайная величина 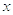 , распределенная по
экспоненциальному закону описывается следующей плотностью распределения:
, распределенная по
экспоненциальному закону описывается следующей плотностью распределения:
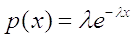
где 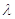 - постоянная положительная величина.
- постоянная положительная величина.
Графики плотности и функции распределения показаны на рисунке
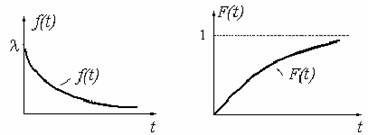
Экспоненциальному распределению, как правило, подчиняется
случайный интервал времени 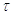 между поступлениями
заявок в систему массового обслуживания. Поэтому весьма важно уметь
моделировать потоки заявок разной интенсивности
между поступлениями
заявок в систему массового обслуживания. Поэтому весьма важно уметь
моделировать потоки заявок разной интенсивности 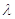 .
.
Математическое ожидание 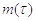 экспоненциально распределенной
случайной величины
экспоненциально распределенной
случайной величины 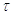 равно:
равно:
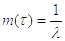
а дисперсия
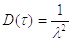
Чтобы найти алгоритм имитации экспоненциально
распределенных чисел 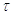 ,
применим метод инверсии:
,
применим метод инверсии:

где  –
случайное число, равномерно распределённое на интервале
–
случайное число, равномерно распределённое на интервале  .
.
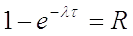
откуда
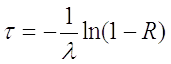
но, поскольку случайная величина 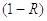 распределена точно
так же, как
распределена точно
так же, как  , и находится
в том же интервале
, и находится
в том же интервале  ,
то последнюю формулу можно заменить на более удобную форму:
,
то последнюю формулу можно заменить на более удобную форму:
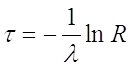
Таким образом мы находим (генерируем) случайную
величину 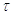 по показательному закону распределения.
по показательному закону распределения.
Необходимость последовательного анализа заключается в его использовании для статистического решения многих задач практического характера, в которых необходима проверка гипотетических предположений о параметрах данного в задаче процесса. Статистический анализ даёт подход, который позволяет затратить на заметное количество меньше числа наблюдений для принятия решения среди всех статистических методов с определёнными значениями вероятностей ошибок первого и второго родов.
3.2 Математическая модель последовательного анализа ВальдаПусть
на измеримом пространстве  наблюдается
последовательность независимых одинаково распределенных случайных величин
наблюдается
последовательность независимых одинаково распределенных случайных величин 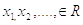 , имеющих плотность
распределения вероятностей
, имеющих плотность
распределения вероятностей 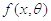 с
параметром
с
параметром 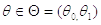 истинное
значение которого неизвестно.
истинное
значение которого неизвестно.
Относительно распределения имеется два предположения:

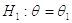
 : наблюдения распределены с плотностью
: наблюдения распределены с плотностью 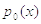
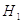 : наблюдения распределены с плотностью
: наблюдения распределены с плотностью 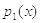
(если
наблюдения дискретны, то 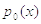 и
и 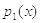 -
вероятности).
-
вероятности).
После каждого наблюдения предоставляется выбор из трех возможных решений:
- принять  и закончить наблюдения,
и закончить наблюдения,
- принять 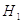 и закончить наблюдения,
и закончить наблюдения,
- не принимать ни одну из гипотез и продолжить наблюдения.
Решающее правило (последовательный критерий отношения вероятностей):
Рассмотрим
следующую процедуру  .
Теперь зафиксируем две граница (два порога):
.
Теперь зафиксируем две граница (два порога):
- верхний 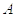
-нижний 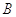
где 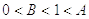 .
.
Пусть уже получено  наблюдений
наблюдений 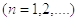 .
.
Для
любого n вероятность получения выборки 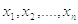 определяется
следующим образом:
определяется
следующим образом:
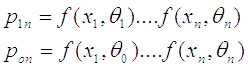
,если
справедлива 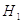
,если
справедлива 
Для
каждой стадии эксперимента, т.е. для каждого испытания при любом  ,
должно вычисляться:
,
должно вычисляться:
Если
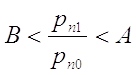
то эксперимент продолжается,
если
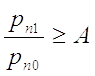
то эксперимент
заканчивается принятием гипотезы 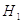 ,
,
если
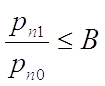
то эксперимент
заканчивается принятием гипотезы  .
.
Величины
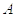 и
и
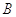 должны
быть заданы так, чтобы критерий имел наперед заданную силу
должны
быть заданы так, чтобы критерий имел наперед заданную силу 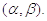
С
практической точки зрения, легче вычислять логарифм 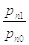 , т.е.
, т.е. 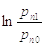 ,
так как он может быть расписан, как сумма из n членов.
,
так как он может быть расписан, как сумма из n членов.
То есть:
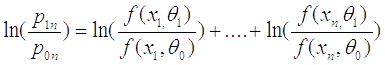
Здесь мы проверяем точно также на каждом шаге эксперимента:
Заменим  и получаем:
и получаем:
Если
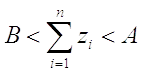
то эксперимент продолжается,
если

то эксперимент
заканчивается принятием 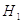 ,
,
если

то эксперимент
заканчивается принятием  .
.
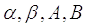
Назовём
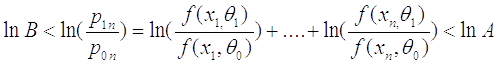
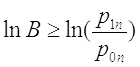
выборкой нулевого типа, а


выборкой первого типа.
Легко заметить,
что вероятность получения любой заданной выборки 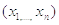 первого типа не
менее, чем в
первого типа не
менее, чем в 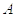 раз
больше при гипотезе
раз
больше при гипотезе 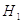 ,
чем при гипотезе
,
чем при гипотезе  .
Значит мера вероятности всех выборок первого типа соответственно не менее, чем
в
.
Значит мера вероятности всех выборок первого типа соответственно не менее, чем
в 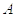 раз больше при
раз больше при 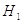 , чем при
, чем при  и эта вероятность
является
и эта вероятность
является 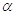 , когда
верна гипотеза
, когда
верна гипотеза  ,
следовательно она и равна
,
следовательно она и равна  ,
если верна
,
если верна 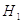 . Значит
получаем:
. Значит
получаем:

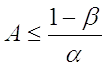
значит,  будет верхней
границей для
будет верхней
границей для 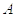 и
и
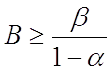
значит 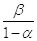 будет нижней
границей для
будет нижней
границей для 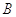 .
.
Таким образом мы
получили оценку верхней и нижней границ 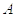 и
и 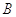 .
.
Генерируются случайные величины по заданному закону,
используя сгенерированные равномерно распределённые случайные величины, с
параметром  .
Находятся границы A и B по данным параметрам силы
.
Находятся границы A и B по данным параметрам силы 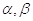 . Начинаем
эксперименты:
. Начинаем
эксперименты:
если
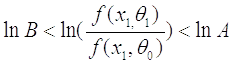
то прибавляем  , если
, если
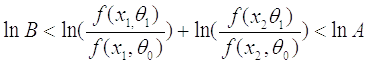
То продолжаем прибавлять 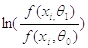 ,
, 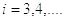 пока это неравенство
не будет иметь смысл, т.е. пока оно не станет меньше
пока это неравенство
не будет иметь смысл, т.е. пока оно не станет меньше 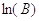 , либо больше
, либо больше 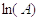 .
.
Если же 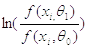 ,
,
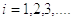 после какого-либо
эксперимента меньше
после какого-либо
эксперимента меньше 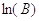 ,
либо больше
,
либо больше 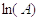 , т.е.
, т.е.
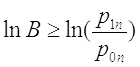 ,
,
то принимаем гипотезу  , а если
, а если
 ,
,
то принимаем гипотезу 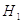 и отклоняется
гипотеза, что случайная величина распределена по закону с параметром
и отклоняется
гипотеза, что случайная величина распределена по закону с параметром  , но этого не может
быть, так как мы и генерируем случайные величины с этим параметром. Значит тест
ошибается.
, но этого не может
быть, так как мы и генерируем случайные величины с этим параметром. Значит тест
ошибается.
Производим данный тест 1000 раз, считаем сколько раз тест ошибается и делим это число на 1000. Полученное число будет ошибкой первого рода.
Затем генерируются случайные величины по заданному
закону, используя сгенерированные равномерно распределённые случайные величины,
с параметром 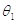 .
Находятся границы
.
Находятся границы 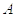 и
и
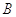 по данным
параметрам силы
по данным
параметрам силы 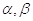 .
Начинаем эксперименты:
.
Начинаем эксперименты:
если
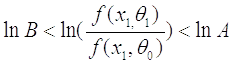
то прибавляем  , если
, если
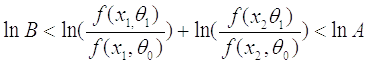
То продолжаем прибавлять 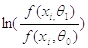 ,
, 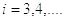 пока это
неравенство не будет иметь смысла, т.е. пока оно не станет меньше
пока это
неравенство не будет иметь смысла, т.е. пока оно не станет меньше 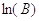 , либо больше
, либо больше 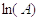 .
.
Если же 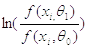 ,
,
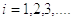 после какого-либо
эксперимента меньше
после какого-либо
эксперимента меньше 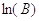 ,
либо больше
,
либо больше 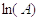 , т.е.
, т.е.
 ,
,
то принимаем гипотезу 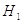 , а если
, а если
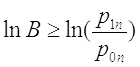 ,
,
то принимаем гипотезу  и отклоняется
гипотеза, что случайная величина распределена по закону с параметром
и отклоняется
гипотеза, что случайная величина распределена по закону с параметром 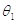 , но этого не может
быть, так как мы и генерируем случайные величины с этим параметром. Значит тест
ошибается.
, но этого не может
быть, так как мы и генерируем случайные величины с этим параметром. Значит тест
ошибается.
Производим данный тест 1000 раз, считаем сколько раз тест ошибается и делим это число на 1000. Полученное число будет ошибкой второго рода.
4 РЕЗУЛЬТАТЫ И ВЫВОД 4.1 Модификация теста и начальные значенияПри проведении экспериментов проверки появления
искажений, мы используем модель тренда статистики критерия для повышения
устойчивости последовательного теста. В работе для проверки ограничений на
параметры статистической модели разработан тест Вальда с использованием тренда
статистики критерия. В каждом тесте задается свой «ограничитель» выборочных
данных 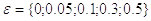 в
зависимости от эксперимента, а также «переключатель состояний»
в
зависимости от эксперимента, а также «переключатель состояний» 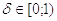 . Также возьмем
«параметр запрета» появления искажений
. Также возьмем
«параметр запрета» появления искажений 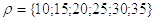 . Столь громоздкая
процедура объясняется тем, что тест является асимптотическим и для
достоверности выводов требуется достаточно большой объем выборки.
. Столь громоздкая
процедура объясняется тем, что тест является асимптотическим и для
достоверности выводов требуется достаточно большой объем выборки.
Задаются начальные данные для теста:
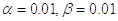
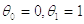
Модификация теста с использованием тренда статистики критерия предполагает некую модификацию данных.
Предполагается следующая модификация:
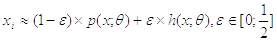
, где
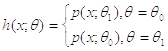 .
.
А также модифицируем элементы сыммы:
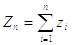
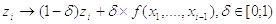
, где
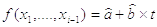
, где 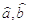 -
ОМП по
-
ОМП по  :
:
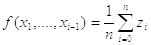 .
.
Таким образом получается тест, определяющий ошибки первого и второго родов последовательных статистических тестов.
Заданный «параметр запрета», использованный в тренде, должен сгладить и оптимизировать тест Вальда за счет своего ограничивающего действия.
4.1.1 РЕЗУЛЬТАТЫ ТЕСТА ВАЛЬДАКак было сказано ранее, для запуска и прохождения
теста Вальда необходимы начальные данные, которые были описаны выше. Фиксируем 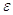 . Тест запускается
1000 раз на одно значение
. Тест запускается
1000 раз на одно значение  .
Значение
.
Значение  распределено
на отрезке
распределено
на отрезке  с шагом
0.1. В сумме тест запускается 50 000 раз, что нужно для объёма выборки,
следовательно, для более достоверных выводов. Ниже представлены графики
зависимости значения ε от среднего числа ошибок первого рода.
с шагом
0.1. В сумме тест запускается 50 000 раз, что нужно для объёма выборки,
следовательно, для более достоверных выводов. Ниже представлены графики
зависимости значения ε от среднего числа ошибок первого рода.
ЗАКЛЮЧЕНИЕ
В ходе данной работы
1)описывается последовательный критерий отношения вероятностей, который применяется на практике;
2) подтверждается гипотеза, которая требует проверки при постановке задачии затем, по получаемым статистическим данным, используя последовательный критерий отношений вероятностей, мы получаем возможность определить верность проверяемой гипотезы;
3) прорабатывается и впоследствии используется теоретический материал, позволяющий понять суть и основные принципы последовательного критерия отношения вероятностей;
4) производится ознакомление с основными положениями последовательного анализа в целом;
5) разбирается теоретический материал относительно последовательных проверок статистических гипотез, который будет использован в дальнейшей работе.
6) модифицируется последовательный тест с использованием тренда статистики для повышения устойчивости.
7) дополняется модификацией с «параметром запрета».
5 ИСТОЧНИКИ
1. Последовательный анализ / А. Вальд: под редакцией В.А. Севастьянова. - Москва, 1960,- 320 с.
2. Исследование распределений статистик критериев тренда и случайности / А.С. Беркович, Б.Ю. Лемешко, А.Ю. Щеглов. –Новосибирск, 210, -Т6, -с.13-17.
3. Робастность байесовских и последовательных статистических решающих правил / А.Ю. Харин. –Минск: БГУ, 2013.-207 с.
4. Прикладная стохастика: робастность, оценивание, прогноз / А.М. Шурыгин. –Москва: Финансы и статистика, 2000. -223 с.
ПРИЛОЖЕНИЕ
|
package main; |














 (zip - application/zip)
(zip - application/zip)










