Филиал государственного бюджетного образовательного учреждения высшего профессионального образования Московской области «Международный университет природы, общества и человека «Дубна» - Дмитровский институт непрерывного образования (филиал ДИНО университета «Дубна»)
Кафедра математики и прикладной информатики
|
КУРСОВАЯ РАБОТА ПО ДИСЦИПЛИНЕ |
|
«ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ ВЫСОКОГО УРОВНЯ» |
ТЕМА: «Разработка программы вычисления обратной матрицы»
Выполнила: студентка
0215-ЭК(о) группы
первого курса
направление: ПИ
Кондратьева Наталья Дмитриевна
Руководитель:
к.т.н., доцент Завьялов А.М.
Дата защиты:____________
Оценка: ________________
________________________
(подпись руководителя)
г. Дмитров, 2016
Оглавление
Оглавление. 2
Введение. 3
Постановка задачи. 4
Метод Гаусса (метод последовательного исключения неизвестных) 5
БЛОК-СХЕМА.. 7
Интерфейс. 8
Листинг программы.. 10
Вывод. 17
Список используемой литературы.. 18
Введение
Данная курсовая работа является обобщающим итогом полученных знаний за 1-ый курс по “Программированию на языках высокого уровня” и “Линейной алгебре”. В данной работе мы рассмотрим алгоритм создания программы, которая сможет вычислять обратную матрицу. Также мы рассмотрим теоретическую часть, блок – схему и непосредственно сам листинг программы.
Постановка задачи
Цель: создание программы способной вычислять обратную матрицу
Исходные данные: Теория (решение обратной матрицы методом Гаусса - Жордана), среда разработки (Microsoft Visual Basic 6.0)
Представлении о модели:
- В программу можно вводить нужные нам данные
- Выдавать пользователю ответ
- Выдавать пользователю дополнительную информацию (Список разрешающих строк, исходную матрицу, конечную информацию)
- Иметь удобную навигационную систему
- Корректно выполнять решение
Ожидаемый результат: Корректно работающая программа
Критерии оценки результата: Главным критерием является в первую очередь правильность вычисления обратной матрицы. Также можно отнести к критериям удобство использования программы.
Нахождение обратной матрицы методом Гаусса-Жордана.
Суть нахождения обратной матрицы методом Гаусса-Жордана заключается в том, что если с единичной матрицей Е провести элементарные преобразования, которыми невырожденная квадратная матрица А приводится к Е, то получится обратная матрица A-1 .
Теперь опишем алгоритм приведения матрицы А порядка n на n, определитель которой не равен нулю, к единичной матрице. Для начала преобразуем матрицу так, чтобы элемент a11 стал равен единице, а все остальные элементы первого столбца стали нулевыми.
Если a11=0, то на место первой строки ставится k-ая строка (k>1), в которой ak1 ≠0, а на место k-ой строки ставится первая. (Строка с ak1 ≠0 обязательно существует, в противном случае матрица A – вырожденная). После перестановки строк получили «новую» матрицу А, у которой ak1 ≠0.
Теперь умножаем каждый элемент первой строки на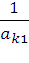 
. Так приходим к «новой» матрице А, у которой a11=1. Далее к элементам второй строки прибавляем
соответствующие элементы первой строки, умноженные на -a21 . К элементам третьей строки – соответствующие элементы
первой строки, умноженные на –a31. И продолжаем такой процесс до n-ой строки включительно. Так все элементы
первого столбца матрицы А,
начиная со второго, станут нулевыми.
Преобразуем матрицу А так, чтобы элемент a22 стал равен единице, а все остальные элементы второго столбца, начиная с a32 , стали нулевыми.
Если a22=0, то на место второй строки ставится k-ая строка (k>2), в которой ak2 ≠0, a на место k-ой строки ставится вторая. Так получаем
преобразованную матрицу А,
у которой a22 ≠0. Умножаем все
элементы второй строки на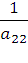 
. После этого к элементам третьей строки прибавляем
соответствующие элементы второй строки, умноженные на –a32. К элементам четвертой строки – соответствующие элементы
второй строки, умноженные на –a42. Следует продолжить такой процесс до n-ой строки включительно. Так все элементы
второго столбца матрицы А,
начиная с третьего, станут нулевыми, а a22 будет равен единице.
Продолжаем процесс, пока все элементы главной диагонали матрицы А не станут равными единице, а все элементы ниже главной диагонали не станут равными нулю. С этого момента начинаем обратный ход метода Гаусса-Жордана. Теперь преобразуем матрицу А так, чтобы все элементы n-ого столбца, кроме ann, стали нулевыми. Для этого к элементам (n-1)-ой строки прибавляем соответствующие элементы n-ой строки, умноженные на –an-1n . К элементам (n-2)-ой строки – соответствующие элементы n-ой строки, умноженные на –an-2n . Такой процесс продолжаем до первой строки включительно. Так все элементы n-ого столбца матрицы А (кроме ann), станут нулевыми.
Преобразуем матрицу А так, чтобы все элементы (n-1)-ого столбца до an-1n-1 , стали нулевыми. Для этого к элементам (n-2)-ой строки прибавляем соответствующие элементы (n-1)-ой строки, умноженные на -an-2n-1 . К элементам (n-3)-ой строки – соответствующие элементы (n-1)-ой строки, умноженные на -an-3n-1 . И продолжаем такой процесс до первой строки включительно. Так все элементы (n-1)-ого столбца матрицы А (кроме an-1n-1 ), станут нулевыми. Действуя дальше схожим образом, мы получим единичную матрицу.
Пример №1:
Требуется найти для исходной матрицы А обратную матрицу А-1 методом Гауcса.
Пример 1. Методом исключения Гаусса найдем матрицу, обратную к матрице
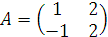
Решение:
К матрице A справа приписываем единичную матрицу того же порядка (А|E)
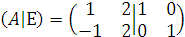
Приведем Матрицу (А|E) элементарными преобразованиями первого и второго типов к ступенчатому виду
→
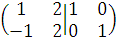Последняя матрица имеет ступенчатый вид
3. Далее выписываем обратную матрицу. Это матрица, стоящая справа в последней преобразованной матрице.
В последней матрице слева стоит единичная матрица E.
Тогда матрица A-1 будет иметь следующий вид:
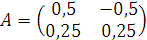
Пример №2.
Методом Гаусса найдем матрицу, обратную к матрице
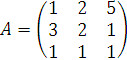
Решение:
К матрице А справа припишем единичная матрица того же порядка (А|E)
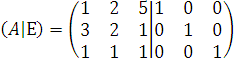
Матрица (А|E) приводится элементарными преобразованиями первого и второго типов к ступенчатому виду
поменяем местами вторую и третью строки
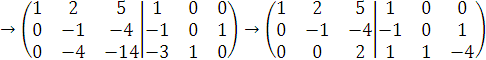
Последняя матрица имеет ступенчатый вид.
3. Полученная ступенчатая матрица элементарными преобразованиями 1-го, 2-го и 3-го типов приводим к виду, где слева будет матрица Е. Затем преобразования начинаются с последней строки.
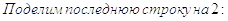
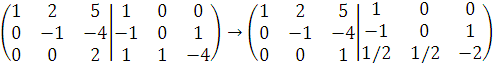
К элементам второй строки прибавляем элементы третьей, умноженные на 4, а к элементам первой строки - элементы третьей, умноженные на 5:
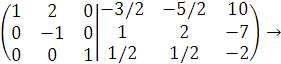
Все элементы второй строки умножим на (-1).
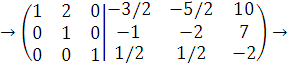
Из элементов первой строки вычитаем элементы второй, умноженные на 2.
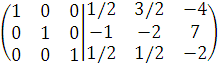
4. Выписывается обратная матрица. Это матрица, стоящая справа в последней преобразованной матрице.
В последней матрице слева стоит единичная матрица E.
Тогда матрица A-1=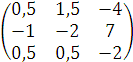
БЛОК-СХЕМА
Условные обозначения:
· MATR – матрица;
· B – вспомогательный столбец;
· ROW – текущая строка;
· X – обратная матрица;
· N – размерность матрицы;
· I – рабочая переменная;
· J – рабочая переменная;
· K – рабочая переменная;
· TMP – рабочая переменная.
· FLAG– флаг, определяющий являются ли элементы матрицы нулевыми;
· GET_B – функция, преобразует входную матрицу в диагональную;
· RES – флаг, определяющий возможно ли получить обратную матрицу;
Блок-схема представлена на рисунке 1.
Рисунок 1.
Интерфейс
Рассмотрим главную форму:
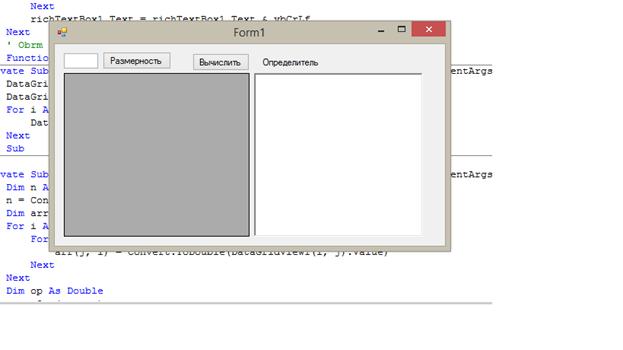Рис.1. Интерфейс программы
На главной форме №1 расположен:
· Панель управления
с помощью кнопок мы управляем ходом выполнения решения
o Размерность - кнопка, с помощью которой мы задаем размерность какой-либо матрицы
o Вычислить - кнопка, с помощью которой производится нахождение обратной матрицы
· Определитель - здесь выводится определитель матрицы
· Окно вывода ответов – здесь выводятся результаты
· Окно ввода размерности – сюда вводится размерность матрицы
· Окно ввода информации - сюда вводятся элементы матрицы
Рассмотрим форму №2:
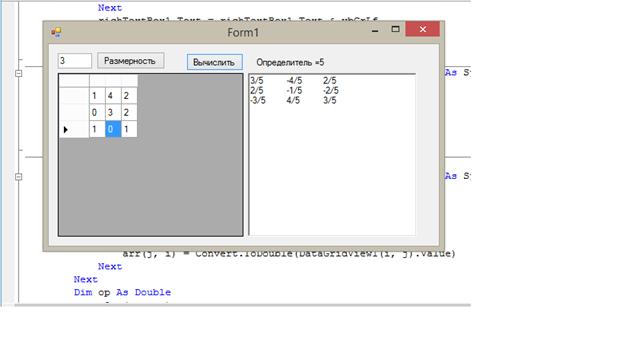
Рис.2. Результаты работы программы
На побочной форме №2 выводится - Дополнительная информация:
o Первоначальная матрица
o Обратная матрица
o Определитель
Программный код
Public Class Form1
Function Opr(ByRef c(,) As Double, ByVal n As Integer) As Double
Dim k, p, q, t, l
Dim sum
" Dim b
Dim b(n - 2, n - 2) As Double
sum = 0
If n = 2 Then
sum = c(0, 0) * c(1, 1) - c(0, 1) * c(1, 0)
Else
For k = 0 To n - 1
For p = 1 To n - 1
q = 0
t = 0
While q < n - 1
If q = k Then
t = t + 1
End If
b(p - 1, q) = c(p, t)
q = q + 1
t = t + 1
End While
Next
If k Mod 2 = 1 Then
sum = sum - c(0, k) * Opr(b, n - 1)
Else
sum = sum + c(0, k) * Opr(b, n - 1)
End If
Next
End If
Opr = sum
End Function
Function Obrm(ByRef m1(,) As Double, ByVal n As Integer, ByVal o As Double) As Double
Dim i, j As Integer
Dim mas11(n - 1, n - 1), m2(n - 1, n - 1) As String
i = 0
Dim k, p, q, t, l
Dim sum
Dim b(n - 2, n - 2) As Double
sum = 0
If n = 2 Then
mas11(0, 0) = m1(1, 1) * (o ^ (-1))
mas11(0, 1) = (-m1(1, 0)) * (o ^ (-1))
mas11(1, 0) = (-m1(0, 1)) * (o ^ (-1))
mas11(1, 1) = (m1(0, 0)) * (o ^ (-1))
Else
For i = 0 To n - 1
For k = 0 To n - 1
q = 0
t = 0
For p = 0 To n - 1
t = 0
For j = 0 To n - 1
If p = i Or j = k Then
Else
b(q, t) = m1(p, j)
t += 1
End If
Next
If t > 0 Then q += 1
Next
sum = (-1) ^ (i + k) * Opr(b, n - 1)
If Math.Abs(o) > 2 Then
If (sum < 0 And o < 0) Then
mas11(i, k) = Math.Abs(sum) & "/" & Math.Abs((o))
ElseIf (sum < 0 And o > 0) Or (sum > 0 And o < 0) Then
mas11(i, k) = "-" & Math.Abs(sum) & "/" & Math.Abs(o)
Else
mas11(i, k) = Math.Abs(sum) & "/" & Math.Abs((o))
End If
Else
mas11(i, k) = sum * (o ^ (-1))
End If
sum = 0
Next
Next
End If
For i = 0 To n - 1
For k = 0 To n - 1
m2(i, k) = mas11(k, i)
richTextBox1.Text = richTextBox1.Text & CStr(m2(i, k)) & vbTab
Next
richTextBox1.Text = richTextBox1.Text & vbCrLf
Next
" Obrm = sum
End Function
Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click
DataGridView1.RowCount = Convert.ToInt32(TextBox1.Text)
DataGridView1.ColumnCount = Convert.ToInt32(TextBox1.Text)
For i As Integer = 0 To Convert.ToInt32(TextBox1.Text) - 1
DataGridView1.AutoResizeColumn(i)
Next
End Sub
Private Sub Button2_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button2.Click
Dim n As Integer
n = Convert.ToInt32(TextBox1.Text)
Dim arr(n, n) As Double
For i As Integer = 0 To n - 1
For j As Integer = 0 To n - 1
arr(j, i) = Convert.ToDouble(DataGridView1(i, j).Value)
Next
Next
Dim op As Double
op = Opr(arr, n)
label1.Text += " =" + op.ToString()
If op = 0 Then
MessageBox.Show("Определитель равен нулю! Вычислить обратную матрицу нельзя.")
Else
Obrm(arr, n, op)
End If
End Sub
End Class
Вывод
Итогом работы можно считать созданную функциональную модель вычисления обратной матрицы методом исключения Гаусса, используя среду разработки Microsoft Visual Basic 6.0. Данная модель применима к невырожденным матрицам, то есть определитель которых не равен нулю. Созданная функциональная модель вычисления обратной матрицы и ее программная реализация могут служить органической частью решения более сложных задач.
Список используемой литературы
1. Симанков, В.С. Основы функционального программирования [Текст] / В.С. Симанков, Т.Т. Зангиев, И.В. Зайцев. – Краснодар: КубГТУ, 2002. – 160 с.
2. Архангельский, Н.А. Вычислительные методы алгебры в приемах и задачах. [Текст] / Н.А. Архангельский – М.: МАИ, 2001. C. 812.
3. Степанов, П.А. Функциональное программирование на языке Lisp. [Электронный ресурс] / П.А.Степанов, А.В. Бржезовский. – М.: ГУАП, 2003. С. 79.
4. Хювенен Э. Мир Лиспа [Текст] / Э. Хювенен, Й. Сеппянен. – М.: Мир, 1990. – 460 с.
5. Кремер, Н.Ш. Высшая математика для экономистов: учебник для студентов вузов. [Текст] / Н.Ш.Кремер, 3-е издание – М.:ЮНИТИ-ДАНА, 2006. C. 412.
6. Обратная матрица [Электронный ресурс] – Режим доступа: http://ru/wikipedia.org/wiki/Обратная _матрица.
7. Калиткин, Н.Н. Численные методы. [Электронный ресурс] / Н.Н. Калиткин. – М.: Питер, 2001. С. 504.
8. Семакин, И.Г. Основы программирования. [Текст] / И.Г.Семакин, А.П.Шестаков. – М.: Мир, 2006. C. 346.
|
Дата |
ФИО |
Подпись |
||
|
« » 200__г. |
Кондратьева Н.Д. |
|||
|
Дата |
ФИО |
Оценка |
Подпись |
|
|
« » 200__г. |
Завьялов А.М. |
|||
(zip - application/zip)
Статистика файлового архива
