Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Сыктывкарский государственный университет имени Питирима Сорокина»
(ФГБОУ ВО «СГУ им. Питирима Сорокина»)
Институт точных наук и информационных технологий
Кафедра физико-математического и информационного образования
Курсовая работа
по дисциплине: «Геометрия»
Подобие плоскости
Направление: 500100.62 «Педагогическое образование»
Профиль: «Информатика, Математика»
Исполнитель: обучающийся 1315 группы Амосов Никита Владимирович
Научный руководитель: к.ф.-м.н., доцент, Понарядова Раиса Семёновна.
Сыктывкар, 2015
Оглавление
Введение. 3
Глава I. Преобразование плоскости. 4
Историческая справка. 4
Основные определения. 5
Гомотетия. 7
Свойства гомотетии. 8
Подобные треугольники. 9
Признаки подобия треугольников. 10
Метрические соотношения в прямоугольном треугольнике. 13
Пропорциональные отрезки в круге. 18
Глава II. Задачи на применение. 19
Задачи на движение. 19
Задачи на гомотетию.. 21
Задачи на подобие. 23
Задачи на метрические соотношения в прямоугольном треугольнике. 26
Задачи на пропорциональные отрезки в круге. 27
Заключение. 29
Список литературы. 30
Введение.
Сегодня предметом нашего исследования будет «Подобие плоскости». Почему именно эта тема. Значимость подобий в нашей жизни очевидна и бесспорна, а в школе тема рассматривается очень скудно.
Знание темы помогает нам как на уроках в школе, будь то геометрия или география, так и в повседневной жизни. Особенно растущие потребности технического прогресса требуют научной разработки теории преобразований, обеспечивающих точность отображения объектов на плоскость с соблюдением размеров.
Свойства
подобия, установленные из опыта, издавна широко использовались при составлении
планов, карт, при выполнение архитектурных чертежей различных деталей машин и
механизмов.
Список использования свойств подобия очень большой и особенно актуален в наше
время. Сегодня мы рассмотрим преобразование в школьном курсе геометрии.
Цель курсовой: изучить преобразование плоскости и его свойства и рассмотреть преобразование в школе.
Вытекающие задачи, которые стоят перед нами:
1) Подобрать и изучить материал по рассмотренной теме
2) Рассмотреть сквозь преобразование подобия преобразование движения плоскости
3) Показать применение преобразование подобия к решению задач.
Задачи: а) на построение; б) на доказательство; в) на вычисление;
На примерах рассмотрим использование преобразований плоскости и его свойств. Именно решённые задачи будут итогом курсовой работы.
Глава I. Преобразование плоскости.
Историческая справка.
Искусство изображать предметы на плоскости с древних времен привлекало к себе внимание человека. Попытки таких изображений появились значительно раньше, чем возникла письменность. Ещё в глубокой древности люди рисовали на скалах, стенах, сосудах и прочих предметах быта различные орнаменты, растения, животных. Длинная практика подсказала людям, каким правилам надо следовать, чтобы правильно выразить на плоскости желаемый предмет. Так возникли зачатки учения о соответствии и преобразовании. Инженер и архитектор Дезарг в 1630 г. впервые разработал основы математической теории перспективы. Своими трудами он положил начало изучению перспективных преобразований, под которыми впоследствии стали понимать отображение фигуры, данной в одной плоскости, на другую плоскость посредствам центрального проектирования или ряда последовательных проектирований.
Идея отношения и пропорции зародилась в глубокой древности. Об этом свидетельствуют древнеегипетские храмы, детали гробницы Менеса и знаменитых пирамид в Гизе (III тысячелетие до н.э.), вавилонские зиккураты (ступенчатые культовые башни), персидские дворцы и другие памятники древности. Многие обстоятельства, в том числе особенности архитектуры, требования удобства, эстетики, техники и экономичности при возведении зданий и сооружений, вызвали возникновение и развитие понятий отношения и пропорциональности отрезков, площадей и других величин.
Учение о подобии фигур на основе теории отношений и пропорции было создано в Древней Греции в V - IV вв. до н.э. трудами Гиппократа Хиосского, Архита Тарентского, Евдокса Книдского и др. Оно изложено в VI книге "Начал" Евклида, начинающейся следующим определением: «Подобные прямолинейные фигуры суть те, которые имеют соответственно равные углы и пропорциональные стороны».


 Основные определения
Основные определения
Изложение теории геометрических преобразований начнём с общих определений.

 Фигуры F и F1 называются подобными, если каждой точке фигуры F можно сопоставить точку фигуры F1 так, что для любых двух точек М и N фигуры F и сопоставленных им точек М1 и N1 фигуры F1 выполняется равенство
Фигуры F и F1 называются подобными, если каждой точке фигуры F можно сопоставить точку фигуры F1 так, что для любых двух точек М и N фигуры F и сопоставленных им точек М1 и N1 фигуры F1 выполняется равенство 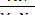 = к, где k — одно и то же положительное число
для всех точек. При этом предполагается, что каждая точка фигуры F1 оказывается сопоставленной какой-то
точке фигуры Р. Число k называется коэффициентом подобия фигур F и F1.
= к, где k — одно и то же положительное число
для всех точек. При этом предполагается, что каждая точка фигуры F1 оказывается сопоставленной какой-то
точке фигуры Р. Число k называется коэффициентом подобия фигур F и F1.
 Если простыми словами, то подобием плоскости называется ее
преобразование, при котором все расстояния между точками умножаются на одно и
то же положительное число. Это число k называется коэффициентом подобия.
Если простыми словами, то подобием плоскости называется ее
преобразование, при котором все расстояния между точками умножаются на одно и
то же положительное число. Это число k называется коэффициентом подобия.
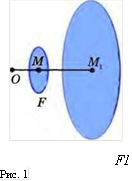
На рисунке 1 представлен способ построения фигуры F1, подобной данной фигуре F. Каждой точке М фигуры F сопоставляется точка М1 плоскости так, что точки М и М1 лежат на луче с началом в некоторой фиксированной точке О, причем ОМ=к-ОМ1 (на рисунке 1 к= 1/3). В результате такого сопоставления получается фигура F1, подобная фигуре F. В этом случае фигуры F и F1 называются центральноподобными.
Примерами подобных четырехугольников являются любые два квадрата, а также два прямоугольника, у которых две смежные стороны одного пропорциональны двум смежным сторонам другого (рис. 2, б).
Примерами подобных фигур произвольной формы являются две географические карты одного и того же района, выполненные в разных масштабах, а также фотографии одного и того же предмета, сделанные в разных увеличениях.
Движение
При k=1 преобразование подобия сохраняет расстояния, т.е. является движением. Следовательно, движение – частичный случай преобразования подобия.

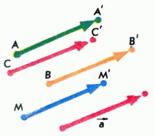 Примерами
движений плоскости являются осевая и центральная симметрия, параллельный
перенос, поворот. Как пример, напомним определение параллельного переноса.
Примерами
движений плоскости являются осевая и центральная симметрия, параллельный
перенос, поворот. Как пример, напомним определение параллельного переноса.
Пусть
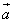 - некоторый вектор плоскости α.
Геометрическое преобразование, переводящее каждую точку
- некоторый вектор плоскости α.
Геометрическое преобразование, переводящее каждую точку 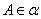 в такую точку
в такую точку 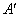 , что
, что 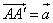 (рис. 3), называется параллельным
переносом на вектор
(рис. 3), называется параллельным
переносом на вектор 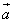 . Параллельный перенос является
движением: если точки
. Параллельный перенос является
движением: если точки 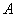 и
и 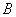 переходят в
переходят в 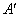 и
и 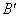 , т.е.
, т.е. 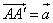 ,
, 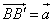 , то
, то 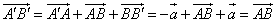 , и потому
, и потому 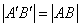 .
.
Свойства движений:
1) Движение переводит прямую в прямые, а параллельные прямые – в параллельные прямые.
2) Движение преводит полуплоскость с границей a в полуплоскость с границей a", где a" – образ прямой a.
3) Движение сохраняет простое отношение трёх точек прямой.
4) Движение сохраняет отношение «Лежать между».
5) Движение переводит отрезок AB в отрезок A"B", где A" и B" – образы точек A и B. При этом середина отрезка AB переходит в середину отрезка A"B".
6) Движение переводит луч в луч, а угол в угол.
7) Движение переводит угол в равный ему угол.
8) Движение переводит взаимно перпендикулярные прямые во взаимно перпендикулярные прямые.
Гомотетия
Расмотрим пример преобразования подбия, отличного от движения. Зададим точку М0 и вещественное число m≠0. Каждой точке М плоскости поставим в соответствие точку M" так, чтобы
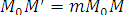 (1)
(1)
Такое
отображение является преобразование плоскости и называется гомотетией.
Точка 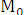 называется гомотетией. Точка М0
называется центром гомотетии, а число m – коэффициентом гомотетии. Докажем, что гомотетия – преобразование
подобия. Действительно, пусть М1 и М2- произвольные точки
плоскости, а
называется гомотетией. Точка М0
называется центром гомотетии, а число m – коэффициентом гомотетии. Докажем, что гомотетия – преобразование
подобия. Действительно, пусть М1 и М2- произвольные точки
плоскости, а 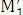 и
и 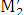 - их образы. Из равенства (1)
получаем:
- их образы. Из равенства (1)
получаем: 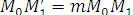 ,
, 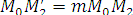 , поэтому
, поэтому
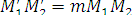 (2)
(2)
Отсюда
получаем: |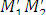 | = |m|×|
| = |m|×|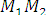 | или
| или 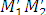 = |m|×
= |m|×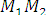 .
.
Таким образом, гомотетия с коэффициентом m является преобразованием подобия с коэффициентом подобия k=|m|.
При m=1 из равенства (1) получаем: 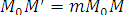 . Отсюда следует, что любая точка М плоскости совпадает с её
образом, т.е. гомотетия с коэффициентом m=1 является тождественным преобразованием. При m=-1 из равенства (1) получаем, что
гомотетия – центральная симметрия. В остальных случаях (т.е. когда |m|≠1) гомотетия – преобразование
подобия, отличное от движения, т.е. преобразование плоскости, не сохраняющее
расстояния между точками.
. Отсюда следует, что любая точка М плоскости совпадает с её
образом, т.е. гомотетия с коэффициентом m=1 является тождественным преобразованием. При m=-1 из равенства (1) получаем, что
гомотетия – центральная симметрия. В остальных случаях (т.е. когда |m|≠1) гомотетия – преобразование
подобия, отличное от движения, т.е. преобразование плоскости, не сохраняющее
расстояния между точками.
Выберем ортонормированный репер (О, E1, E2) так, чтобы точка О совпадала с центром гомотетии. Если М(x, y) – произвольная точка плоскости, а точка М" (x", y") – её образ, то из формулы (1) получаем аналитическое выражение гомотетии:
x"=mx, y"=my (3)
Свойства гомотетии
Рассмотрим простейшие свойства гомотетии.
10. Гомотетия с коэффициентом m≠1 переводит прямую, не проходящую через центр гомотетии, в параллельную ей прямую, а прямую, проходящую через центр гомотетии, — в себя.
Пусть Ax+Bx+С = 0 — уравнение данной прямой l. Подставив сюда значения х. у из (3), получаем уравнение образа l" этой прямой: Ах"+Ву"+Сm = 0. Этим уравнением определяется прямая. Если С≠0, то l||l" ,а если С = 0, то l" и l совпадают.
2° Гомотетия сохраняет простое отношение трех точек.
Пусть A, В и С — три точки прямой, а A", В" и С" — их образы, µ = (AВ, С) и µ"=(А"В, С"). По определению простого отношения трех
точек имеем:  ,
,  . По формуле
. По формуле
(2) получаем: ,
,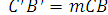 где m — коэффициент гомотетии. Следовательно, m
где m — коэффициент гомотетии. Следовательно, m или
или 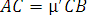 .Таким образом, µ" = µ, т. е. (АВ. С)
= (A"В", С").
.Таким образом, µ" = µ, т. е. (АВ. С)
= (A"В", С").
Из этих свойств следует, что гомотетия переводит отрезок в отрезок, луч в луч и полуплоскость в полуплоскость.
З0. Гомотетия переводит угол в равный ему угол.
Пусть ВАС — данный угол, а В", А" , С" — образы точек В, А и С. По формуле (2) получаем:
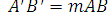 ,
,
Отсюда следует, что В"А"С" = ВАС.
4°. Гомотетия сохраняет ориентацию плоскости.
Пусть (A, B, С) —
произвольный репер, а (А", В", С") — его образ. Используя формулы (4),
получаем: ( ,
, 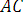 ) | (
) | ( ,
,  ) = m2>0. Итак, в
гомотетии любой репер и его образ ориентированы одинаково, т.е. гомотетия
сохраняет ориентацию плоскости.
) = m2>0. Итак, в
гомотетии любой репер и его образ ориентированы одинаково, т.е. гомотетия
сохраняет ориентацию плоскости.
Подобные треугольники
 Введем понятие подобных треугольников.
Введем понятие подобных треугольников.
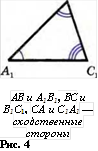
Пусть у двух треугольников АВС и А1В1С1 углы соответственно равны: А=А1, В=В1, С=С1. В этом случае стороны АВ и А1В1, ВС и B1С1 , СА и С1А1 называются сходственными (рис. 4).
 Определение
Определение
 Два треугольника называются подобными, если их углы соответственно равны и
стороны одного треугольника пропорциональны сходственным сторонам другого.
Два треугольника называются подобными, если их углы соответственно равны и
стороны одного треугольника пропорциональны сходственным сторонам другого.
Другими словами, два треугольника подобны, если для них можно ввести обозначения АВС и А1В1С1 так, что
А=А1, В=В1, С=С1 (1)
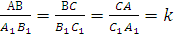 (2)
(2)
Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Подобие треугольников АВС и А1В1С1 обозначается так:
∆АВС ~ ∆А1В1С1
На рисунке 4 изображены подобные треугольники.
Оказывается, что подобие треугольников можно установить, проверив только некоторые из равенств (1) и (2). Рассмотрим три признака подобия треугольников.
Признаки подобия треугольников
Первый признак подобия
 Теорема. Если два угла одного треугольника
соответственно равны двум углам другого, то такие треугольники подобны.
Теорема. Если два угла одного треугольника
соответственно равны двум углам другого, то такие треугольники подобны.
Доказательство
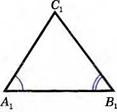 Пусть ∆АВС и ∆А1В1С1
— два треугольника,
у которых ∠А= ∠А1 ∠В=∠В1 (рис. 5). Докажем, что ∆АВС ~ ∆A1B1C1.
Пусть ∆АВС и ∆А1В1С1
— два треугольника,
у которых ∠А= ∠А1 ∠В=∠В1 (рис. 5). Докажем, что ∆АВС ~ ∆A1B1C1.
 По теореме о сумме
углов треугольника ∠С = 180° - ∠А - ∠В , ∠С1 =180° - ∠А1 - ∠B1 и, значит, ∠С=∠С1. Таким образом, углы треугольника АВС соответственно равны углам
треугольника А1В1С1.
По теореме о сумме
углов треугольника ∠С = 180° - ∠А - ∠В , ∠С1 =180° - ∠А1 - ∠B1 и, значит, ∠С=∠С1. Таким образом, углы треугольника АВС соответственно равны углам
треугольника А1В1С1.
Докажем, что стороны треугольника АВС пропорциональны сходственным сторонам треугольника А1В1С1. Так как ∠А = ∠А1 и ∠С=∠С1, то
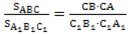
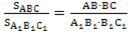
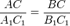
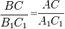 Из этих равенств следует, что . Аналогично,
используя равенства ∠А= ∠А1 ∠В=∠В1, получаем .
Из этих равенств следует, что . Аналогично,
используя равенства ∠А= ∠А1 ∠В=∠В1, получаем .
Итак, стороны треугольника АВС пропорциональны сходственным сторонам треугольника А1В1С1. Теорема доказана.
Второй признак подобия треугольников
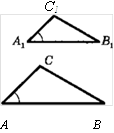 Теорема. Если две стороны
одного треугольника пропорциональны двум сторонам другого треугольника и
углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Теорема. Если две стороны
одного треугольника пропорциональны двум сторонам другого треугольника и
углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Доказательство
Рассмотрим два треугольника АВС и A1B1C1 , у которых , ∠А = ∠А1 (рис. 6, а). Докажем, что ∆АВС ~ ∆A1B1C1. Для этого, учитывая первый признак подобия треугольников, достаточно доказать, что ∠В=∠В1.

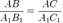 Рассмотрим треугольник АВС2,
у которого ∠1 = ∠А1 , ∠2 = ∠В1 (рис. 6, б). Треугольники АВС2 и А1В1С1
подобны по первому признаку подобия треугольников, поэтому
Рассмотрим треугольник АВС2,
у которого ∠1 = ∠А1 , ∠2 = ∠В1 (рис. 6, б). Треугольники АВС2 и А1В1С1
подобны по первому признаку подобия треугольников, поэтому
.С другой стороны, по условию .
Из этих двух равенств получаем АС=АС2.
Треугольники АВС и АВС2 равны по двум сторонам и углу между ними (АВ — общая сторона, АС=АС2 и ∠А=∠1, поскольку ∠А—∠А1 и ∠1 = ∠А1). Отсюда следует, что ∠В=∠2, а так как ∠2 = ∠В1 то ∠В = ∠В1. Теорема доказана.
Третий признак подобия треугольников
Теорема. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Доказательство
Пусть стороны треугольников АВС и А1В1С1 пропорциональны:
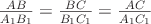 (1)
(1)
Докажем, что ∆АВС и ∆А1В1С1. Для этого, учитывая второй признак подобия треугольников, достаточно доказать, что ∠А=∠А1 Рассмотрим треугольник АВС2, у которого ∠1=∠А1 , ∠2=∠В1 (см. рис. 6, б). Треугольники АВС2 и А1В1С1 подобны по первому признаку подобия
треугольников, поэтому 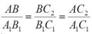 .
.
Сравнивая эти равенства с равенствами (1), получаем: ВС=ВС2, СА=С2А. Треугольники АВС и АВС2 равны по трем сторонам. Отсюда следует, что АА=А 1, а так как ∠1 = ∠А1, то ∠А = ∠А1 Теорема доказана.
Метрические соотношения в прямоугольном треугольнике
Теорема*. В прямоугольном треугольнике перпендикуляр, опущенный из вершины прямого угла на гипотенузу, есть средняя пропорциональная величина между отрезками, на которые основание перпендикуляра делит гипотенузу, а каждый катет есть средняя пропорциональная между гипотенузой и прилежащим к этому катету отрезком гипотенузы.
Пусть AD (рис.7) есть перпендикуляр, опущенный из вершины прямого угла А на гипотенузу ВС. Требуется доказать следующие три пропорции:
1) BD/AD = AD/DC ;
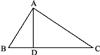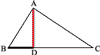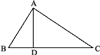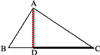
2) BC/AB = AB/BD ; 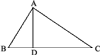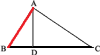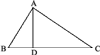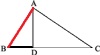
3) BC/AC = AC/DC. 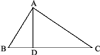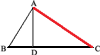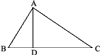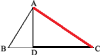

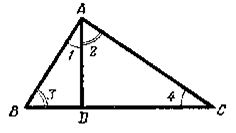
Первую пропорцию мы докажем из подобия треугольников ABD и ADC. Эти треугольники подобны, потому что
∠1 =∠4 и ∠2 = ∠3
как острые углы с соответственно перпендикулярными сторонами. Возьмём в ∆ABD те стороны BD и AD, которые составляют первое отношение доказываемой пропорции; сходственными сторонами в ∆ADC будут AD и DC, поэтому
BD : AD = AD : DC.
Чтобы безошибочно определить, какие стороны взятых
треугольников сходственны между собой, полезно держаться такого пути:
1) указать углы, против которых лежат взятые стороны одного
треугольника;
2) найти равные им углы в другом треугольнике;
3) взять противолежащие им стороны.
Например, для треугольников ABD и ADC рассуждаем так: в.
треугольнике ABD стороны BD и AD лежат против углов 1 и 3; в треугольнике
ADC этим углам равны 4 и 2; против них лежат стороны AD и DC. Значит, стороны
AD и DC сходственны со сторонами BD и AD.
Вторую пропорцию докажем из подобия треугольников ABC и ABD. Эти треугольники подобны, потому что они прямоугольные и острый угол В у них общий. В ∆ABC возьмём те стороны ВС и АВ, которые составляют первое отношение доказываемой пропорции; сходственными сторонами в ∆ABD будут АВ и BD; поэтому
ВС : АВ = АВ : BD.
Третью пропорцию докажем из подобия треугольников ABC и ADC. Эти треугольники подобны, потому что они оба прямоугольные и имеют общий острый угол С.
В ∆АВС возьмём стороны ВС и АС; сходственными сторонами в ∆ADC будут АС и DC; поэтому
ВС : АС = AC: DC.
Следствие. Пусть А (рис.8) есть произвольная точка окружности, описанной на диаметре ВС.

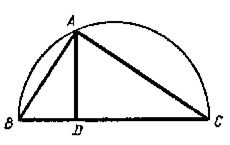
Соединив концы диаметра с этой точкой, мы получим прямоугольный ∆ABC, у которого гипотенуза есть диаметр, а катеты есть хорды (по свойству вписанного угла, опирающегося на диаметр). Применяя доказанную выше теорему к этому треугольнику, приходим к следующему заключению:
Перпендикуляр, опущенный из какой-либо точки окружности на диаметр, есть средняя пропорциональная величина между отрезками, на которые основание перпендикуляра делит диаметр, а хорда, соединяющая эту точку с концом диаметра, есть средняя пропорциональная между диаметром и прилежащим к хорде отрезком диаметра.
Теорема Пифагора. Доказанные выше теоремы позволяют обнаружить замечательное соотношение между сторонами любого прямоугольного треугольника. Это соотношение было впервые замечено греческим геометром Пифагором (VI в. до н. э.) и носит поэтому его имя — теорема Пифагора.
Если стороны прямоугольного треугольника измерены одной и той же единицей, то квадрат длины гипотенузы равен сумме квадратов длин катетов.
Пусть ABC (рис.9) есть прямоугольный треугольник, AD — перпендикуляр, опущенный на гипотенузу из вершины прямого угла.

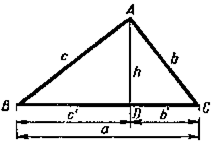
Положим, что стороны и отрезки гипотенузы измерены одной и той же единицей, причём получились числа а, b, с, с" и b" (принято длины сторон треугольника обозначать малыми буквами, соответствующими большим буквам, которыми обозначены противолежащие углы). Применяя теорему*, можем написать пропорции:
а : с = с : с" и а : b = b : b",
откуда
ас" = с2 и ab" = b2.
Сложив почленно эти два равенства, найдём:
ас" + ab" = с2 + b2, или а(с" + b") = с2 + b2.
Но с" + b" = а, следовательно,
a2 = с2 + b2.
Эту теорему обыкновенно выражают сокращённо так: квадрат гипотенузы равен сумме квадратов катетов.
Теорема Пифагора имеет ещё другую формулировку: площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах.
Замечание. Прямоугольный
треугольник со сторонами 3, 4 и 5 называется часто египетским треугольником,
так как он был известен ещё древним египтянам. Так, их землемеры для построения
прямого угла на земной поверхности пользовались таким приёмов: бечёвку
посредством узлов они разделяли на 12 равных частей; затем, связав концы,
натягивали её на земле (посредством кольев) в виде треугольника со сторонами в
3, 4 и 5 делений; тогда угол между сторонами, равными 3 и 4, оказывался прямым.
Прямоугольные треугольники, у которых стороны измеряются целыми числами, носят
название пифагоровых треугольников. Можно доказать, что
катеты х и у и гипотенуза z таких
треугольников выражаются следующими формулами:
х = 2ab, у = а2 — b2, z = а2 + b2 ,
где a и b — произвольные целые числа при условии, что а > b.
Следствие. Квадраты катетов относятся между собой, как прилежащие отрезки гипотенузы. Действительно, из уравнений предыдущего параграфа находим:
c2: b2= ac" : ab" = с": b"
Замечание. К трём равенствам, которые мы вывели выше:
1) ас" = с2; 2) ab" = b2 и 3) a2 = с2 + b2,
можно присоединить ещё следующие два:
4) b" + с" = а и 5) h2 = b"с" "
(если буквой h обозначим длину высоты AD). Из этих равенств третье, как мы видели, составляет следствие первых двух и четвёртого, так что из пяти равенств только четыре независимы; вследствие этого можно по данным двум из шести чисел находить остальные четыре.
Пропорциональные отрезки в круге
Теорема. Произведения отрезков пересекающихся хорд окружности равны.
Доказательство. Пусть хорды AB и CD окружности пересекаются в точке M (рис.10). Треугольники AMC и DMB подобны по двум углам (углы BAC и BDC равны как вписанные углы, опирающиеся на одну дугу), поэтому AM/DM = CM/BM , откуда AM · BM = CM · DM.
Теорема о касательной и секущей.
Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на ее внешнюю часть равно квадрату касательной.
Доказательство. Пусть через точку M (рис.11), лежащую вне окружности, проходят две прямые: одна из них касается окружности в точке A, а вторая пересекает эту окружность в точках B и C, причем точка B лежит между точками M и C.
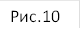

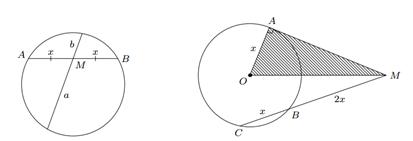
Требуется доказать, что BM · CM = AM2 . Соединим точку A с точками B и C. Рассмотрим треугольники AMB и CMA. Угол при вершине M у них общий, а угол BAM — это угол между касательной AM и хордой AB. Он равен половине дуги AB, заключенной между ними. Но половине этой дуги равен и вписанный угол ACB. Поэтому треугольники AMB и CMA подобны по двум углам. Следовательно, AM/CM = BM/AM , откуда
BM · CM = AM2.
Глава II. Задачи на применение
Задачи на движение
Задача на построение.
1)
 Даны точка О и прямая b. Постройте прямую, на которую
отображается прямая b при центральной
симметрии с центром O.
Даны точка О и прямая b. Постройте прямую, на которую
отображается прямая b при центральной
симметрии с центром O.
2)

Даны две прямые a и b.Постройте
прямую, на которую отображается прямая b при осевой симметрии с осью a.
Задача на вычисление.
Вычислить координаты центра поворота, заданного формулами:
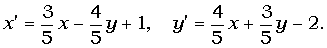
Решение. Центр поворота – инвариантная точка, т. е.
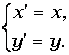
Решим систему:


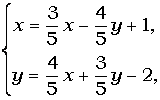 |
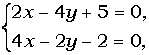
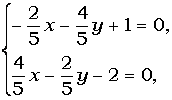
умножим второе уравнение системы на 2 и сложим 1 и 2, получим:
6x-15=0 ; x=2,5 ; y=0;
Ответ: x=2,5 ; y=0;
Задача на доказательство.
На сторонах параллелограмма ABCD вне его построены правильные треугольники ABM, BCK, CDP, DAH. Доказать, что точки M,K,P и H являются вершинами параллелограмма.
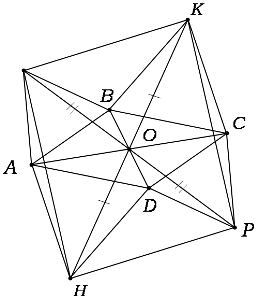
Решение. Рассмотрим центральную симметрию (поворот на 1800) относительно точки О. Пусть - центральная симметрия f(B)=D, f(a)=C, f(C)=A.
При центральной симметрии f, ∆BCK (правильный) перейдет в рамный ему ∆DAH (правильный), по свойствам осевой симметрии (углы сохраняются). Аналогично ∆AMB переходит в ∆CPD.
f(M)=P , f(K)=H → KO=OH, MO=OP → по признаку параллелограмма, KPHM– параллелограмм.
Задачи на гомотетию
Задача на доказательство.
Докажите, что все графики функций у=ах2 (а≠0) гомотетичны.
Решение. Задача будет решена, если мы покажем что график Fа функции у=ах2 гомотетичен графику F функции у=х2 (рис.12). Проведем через начало координат О прямую р, заданную уравнением у=кх, к≠0. Прямая р пересечет графики F и Fа в начале координат, а также в точках Х=(к, к2) и
Ха=(  ,
,  ).
).
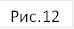
И теперь становится ясно, что вектор 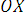 =а
=а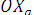 , т.е. точка Х является образом
точки Хa при гомотетии с центром О и коэффициентом
а. А потому и параболу Fa
эта гомотетия переводит в параболу F, т.е. эти параболы гомотетичны.
, т.е. точка Х является образом
точки Хa при гомотетии с центром О и коэффициентом
а. А потому и параболу Fa
эта гомотетия переводит в параболу F, т.е. эти параболы гомотетичны.
Задача на построение.
В данный треугольник АВС вписать квадрат.
Говорят, что многоугольник вписан в некоторую фигуру, если его вершины лежат на границе этой фигуры.
Решение. Сначала построим какой-нибудь квадрат MNPQ, у которого сторона MN лежит на стороне АВ треугольника АВС, а вершина Q лежит на его стороне АС (рис.13,а).
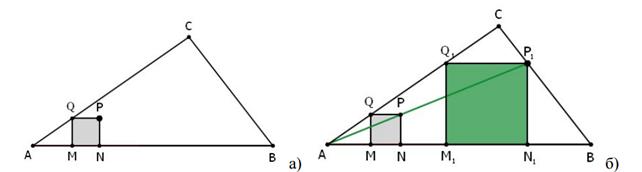 Пусть луч
АР пересекает сторону ВС в некоторой точке Р1. Рассмотрим теперь
гомотетию f с центром А и коэффициентом к=АР1:АР. Эта гомотетия и
переведет квадрат MNPQ в квадрат M1N1P1Q1,
который вписан в треугольник АВС (рис.13,б).
Пусть луч
АР пересекает сторону ВС в некоторой точке Р1. Рассмотрим теперь
гомотетию f с центром А и коэффициентом к=АР1:АР. Эта гомотетия и
переведет квадрат MNPQ в квадрат M1N1P1Q1,
который вписан в треугольник АВС (рис.13,б).
 |
Замечание. Решение этой задачи типично для решения задач на построение методом гомотетии. Используя этот метод, сначала строим какую-нибудь фигуру, гомотетичную искомой и удовлетворяющую всем условиям задачи, за исключением какого-либо одного. Затем, выполняя соответствующую гомотетию, находим решение задачи.
Задачи на подобие
Задачи на доказательство.
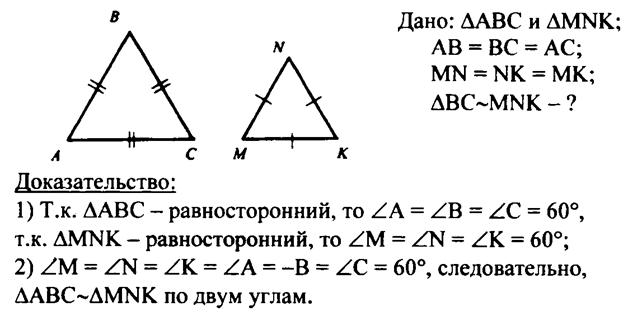 1)Докажите, что два равносторонних
треугольника подобны.
1)Докажите, что два равносторонних
треугольника подобны.
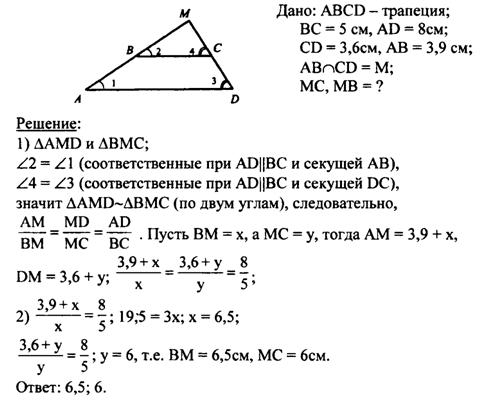 |
2) Основания трапеции равны 5 см и 8 см. Боковые стороны, равные 3,6 см и 3,9 см, продолжены до пересечения в точке М. Найдите расстояния от точки М до концов меньшего основания.
Задача на вычисление.
На одной из сторон данного угла А отложены отрезки АВ=5см и АС=16см. На другой стороне этого же угла отложены отрезки AD=8см и AF=10см. Подобны ли треугольники ACD и AFB? Ответ обоснуйте.
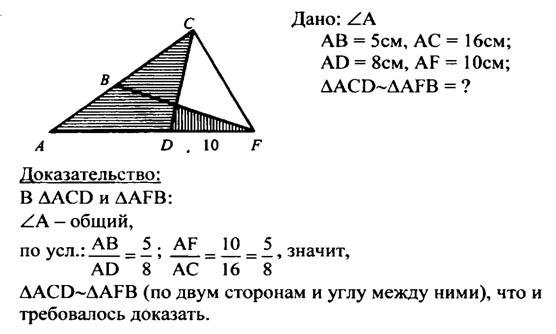
Задача на построение.
Построить треугольник по двум углам и биссектрисе при вершине третьего угла.
Построение. Дано: ∠А= α, ∠В=β, CD - биссектриса третьего угла (см. Рис. 14).
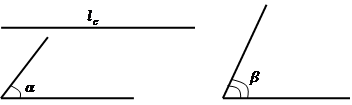
Рис. 14
Выберем произвольный отрезок A1B1 и строим на нем треугольник ∆А1В1С по стороне и двум углам ∠А= α, ∠В=β. В построенном треугольнике проводим биссектрису из угла C, и если она не совпала с указанной в условии биссектрисой, то строим CD. Затем через точку D проводим прямую AB || A1B1 до пересечения с продолжениями сторон CA1 и СB1 треугольника ∆А1В1С. Искомый треугольник ∆АВС построен. Углы ∠А = ∠А1 = α, ∠В=∠В1=β как соответственные при параллельных прямых, CD необходимая биссектриса (см. Рис. 15).

Рис. 15
Построено.
Задачи на метрические соотношения в прямоугольном треугольнике
Задачи на построение.
Построить отрезок, средний пропорциональный между двумя отрезками а и b.
Задачу эту можно решить двояким путём:
1) На произвольной прямой (рис.16) откладываем отрезки АВ = а и ВС = b; на АС, как на диаметре, описываем полуокружность; из В восставляем до пересечения с окружностью перпендикуляр BD. Этот перпендикуляр и есть искомая средняя пропорциональная между АВ и ВС.
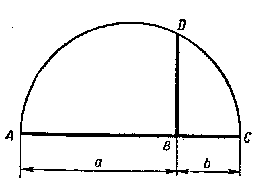
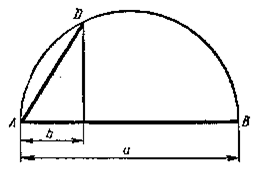
Рис.16 Рис. 17
2) На произвольной прямой (рис.17) откладываем от точки А отрезки а и b. На большем из этих отрезков описываем полуокружность. Проведя из конца меньшего отрезка перпендикуляр к АВ до пересечения его с окружностью в точке D, соединяем А с D. Хорда AD есть средняя пропорциональная между а и b.
Задачи на пропорциональные отрезки в круге
Задача на доказательство.
Хорды AB и CD окружности пересекаются в точке M, причем AM = AC. Докажите, что продолжения высот AA1 и DD1 треугольников CAM и BDM пересекаются на окружности.
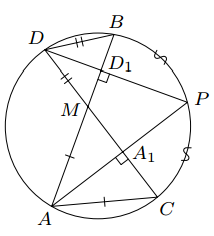 Решение. Треугольники CAM и BDM подобны по
двум углам (рис. 18). По условию один из них равнобедренный, значит, второй
также равнобедренный. Высоты равнобедренных треугольников, проведенные к
основанию, являются биссектрисами углов при вершинах, т. е. лучи AA1
и DD1 биссектрисы равных вписанных углов BAC и BDC. Каждая из этих
биссектрис делит дугу BC пополам, следовательно, они проходят через одну точку
на окружности середину P дуги BC.
Решение. Треугольники CAM и BDM подобны по
двум углам (рис. 18). По условию один из них равнобедренный, значит, второй
также равнобедренный. Высоты равнобедренных треугольников, проведенные к
основанию, являются биссектрисами углов при вершинах, т. е. лучи AA1
и DD1 биссектрисы равных вписанных углов BAC и BDC. Каждая из этих
биссектрис делит дугу BC пополам, следовательно, они проходят через одну точку
на окружности середину P дуги BC.
Задача на вычисление.
Из точки M, расположенной вне окружности на расстоянии √7 от центра, проведены касательная MA (A — точка касания) и секущая, внутренняя часть которой вдвое меньше внешней и равна радиусу окружности. Найдите радиус окружности.

Рис.19
Решение.
Пусть секущая пересекает окружность с центром O (рис. 19) в точках B и C (B между C и M). Обозначим через x радиус окружности. Тогда BC = x и BM = 2x. Если AM — касательная к окружности, то по теореме о касательной и секущей AM2 = BM · CM = 2x · 3x = 6x2. С другой стороны, по теореме Пифагора из прямоугольного треугольника OAM находим, что AM2 = OM2 – OA2 = 7 – x2. Из
уравнения 6x2 = 7 – x2 находим, что x = 1.
Заключение
В данной курсовой мы изучили преобразование плоскости и рассмотрели его свойства. Узнали что такое движение, что такое гомотетия. Вспомнили признаки подобия треугольников и открыли для себя метрические соотношения в прямоугольном треугольнике и пропорциональные отрезки в круге.
Изучив преобразования плоскости и его свойства рассмотрели различные задачи на построение, на доказательство, и на вычисление. Всё это на основе изученной темы.
Соответственно, поставленные задачи курсовой работы выполнены.
Список литературы.
· Геометрия, 7-9; Учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов и др. – 13-е изд.- М.: Просвещение, 2003.- 384 с.: ил.
· Геометрия. В2-х ч. Ч.I. Учебное пособие для студентов физ-мат. фак. пед. ин-тов.- М.:Просвещение. 1986.336с.,ил.
· Геометрия: Учебник для 7-9кл. общеобразоват. учреждений. / Поде редакцией Ф.Я. Цукаря.- 2-е изд.- М.: Просвещение, 1994.- 383 с.: ил.
· Элементарная математика. Геометрия. Сканави М.И. 2-е изд., перераб. и доп., М.: 1974г. - 592с.
· Понарин, Я.П. Элементарная геометрия: Планиметрия, преобразования плоскости [Текст]: в 2 т. / Я.П. Понарин — М.: МЦНМО, 2004.– 312 с. – 1 т.
· http://sernam.ru/book_e_math.php?id=26
· http://oldskola1.narod.ru/KisRibDop/0003.htm














 (zip - application/zip)
(zip - application/zip)